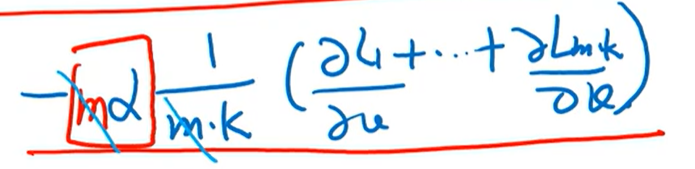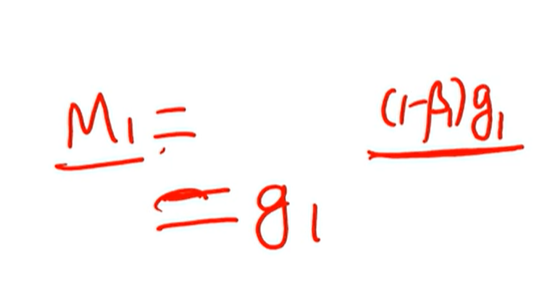7 - 网络优化与正则化
本文最后更新于:3 个月前
[√] 7.0 - 网络优化与正则化

alec:
- 为了模型能够在未知的数据上效果更好,我们希望模型的泛化错误更小。
- 为了提高模型的泛化能力,我们通常会对模型的复杂度进行约束,也就是正则化。
- 优化和正则化是一对矛盾体,就希望好,有希望不要太好。正则化会使训练集上的误差升高,但是会降低训练集和测试集的差别。
- 正则化用来提高模型的泛化能力。

[√] 7.1 - 神经网络优化的特点
[√] 神经网络优化的难点
alec:
- 结构差异大
- 网络类型多样,没有通用的优化算法
- 超参数非常多
- 非凸优化问题
- 参数初始化(不同的参数初始化可能导致不同的局部最优解)
- 非凸优化问题,存在局部最优解,如何逃离局部最优问题(到达梯度为0的鞍点,如何逃出去?)
- 梯度消失、梯度爆炸问题
- 网络非常深的时候,深层的梯度,要么为0、要么非常大
alec:
- 两个角度解决,一方面找到更好的算法、另一方面改进网络结构(例如加上批量规范化,提高网络优化的能力)
[√] 高维空间的非凸优化问题
[√] 鞍点
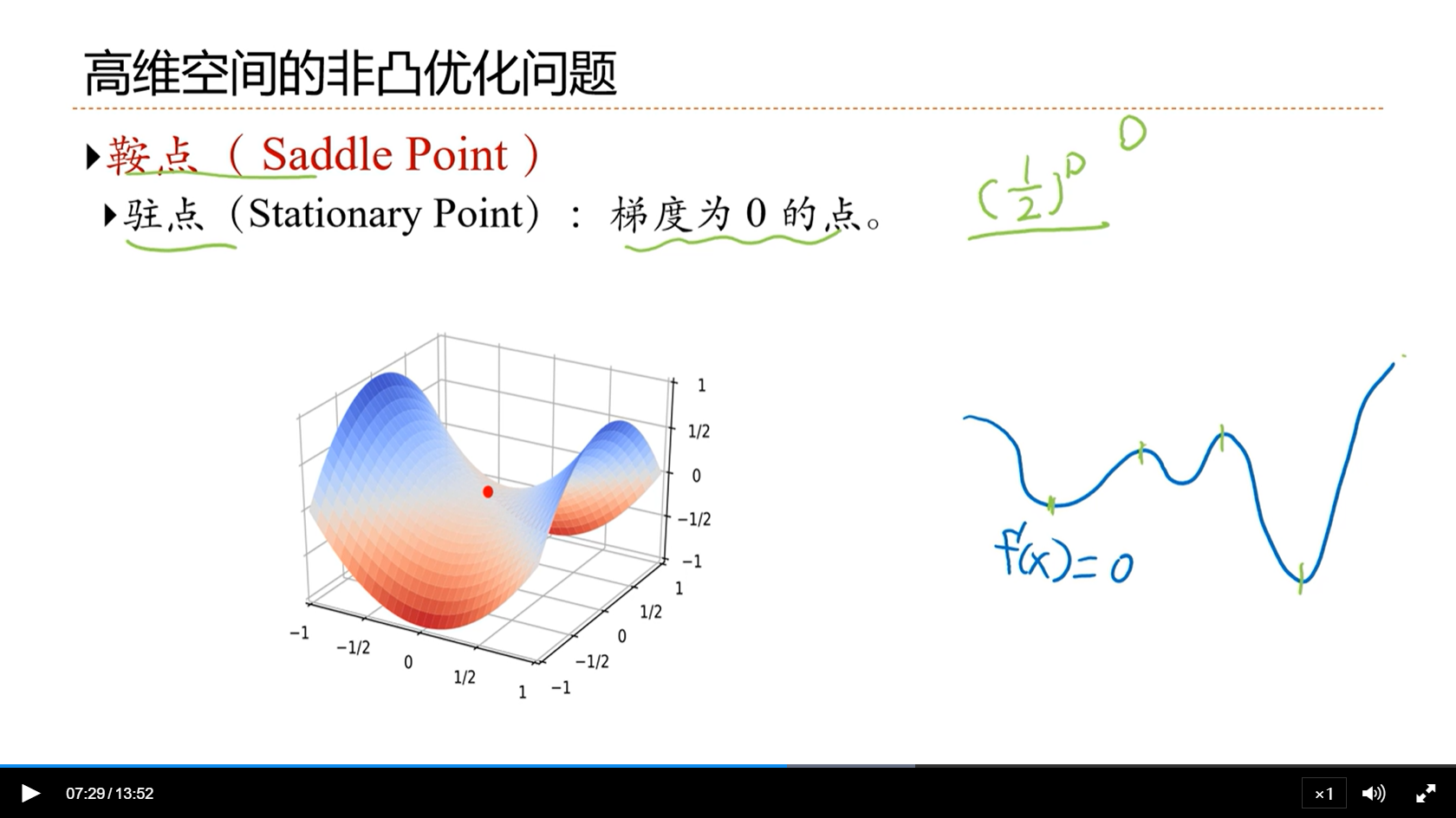
alec:
- 在高维空间要解决的问题,不是如何逃离局部最优点,而是如何逃离鞍点
- 在高维空间,在鞍点中,一个点是局部最低点和局部最高点的比例基本上1:1的,所以在一个D维的空间中,一个点是驻点(所有的维度上都是最小的)的概率大约是二分之一的D次方,这个概率是非常小的,因此在高维空间中,大部分的鞍点都不是驻点,鞍点是驻点的概率是二分之一的N次方,所以高维空间中,鞍点(非驻点)的概率是非常高的。所以在高维空间中,非凸优化问题变成了如何逃离鞍点。
[√] 平坦最小值(Flat Minima)

alec:
- 高维空间中,大部分的局部最优解对应的损失可能非常接近于全局最优解,这个损失已经足够小了,所以有时候我们不需要找到全局最优解,找到一个足够小的局部最优解就够了。而且找到全局最优解,意味着可能就会过拟合了。
- 正则化的作用也是让NN找足够合适的局部最优解,而不是找可能过拟合的全局最优点。因为数据不可能做到百分之百完备,那么找到的全局最优解,就会是过拟合的。月满则亏,水满则溢。
[√] 优化地形(Optimization Landscape)的可视化

alec:
- 加上残差连接之后,地形就变得非常光滑,因此这个网络更加的好优化。
- 残差连接的作用1:残差连接可以缓解梯度消失问题,通过残差连接可以让梯度一直+1
- 残差连接的作用2:使得优化地形更加的平滑,从而使得优化的效率更高
[√] 神经网络优化的改善方法

alec:
- 修改网络结构的目的是为了得到更好的优化地形,是优化神经网络的方法之一
- 神经网络优化的思路:
- 更有效的优化算法:学习率调整、梯度估计调整(此处的优化算法指的是狭义的优化算法,即通过梯度下降进行参数更新的算法)
- 参数初始化、数据预处理
- 修改网络结构:更好的优化地形
- 更好的超参数优化方法
[√] 7.2 - 优化算法改进
alec:
- 更有效的优化算法:学习率调整、梯度估计调整(此处的优化算法指的是狭义的优化算法,即通过梯度下降进行参数更新的算法)
[√] 优化算法:随机梯度下降

[√] 优化算法:小批量随机梯度下降(MiniBatch)

alec:
- 为了改进优化的效率,通常使用小批量随机梯度下降
- 更加充分的利用GPU的并行计算能力
- 小批量梯度下降中每个批次计算出来的梯度,带有随机性,因此并不是最优的
- 优化优化算法的三个考虑角度:
- 批量K
- 梯度
- 学习率
[√] 批量大小(Batch Size)

alec:
- 批量小的时候,随机性更高,因此要设置更小的学习率。因此学习率和批量大小要成正相关。
- K和α的关系:线性缩放原则
- 如图所示,二者线性关系的话,每一步走的距离大体上是不变的
- (此处存疑)
[√] 批量大小对收敛的影响
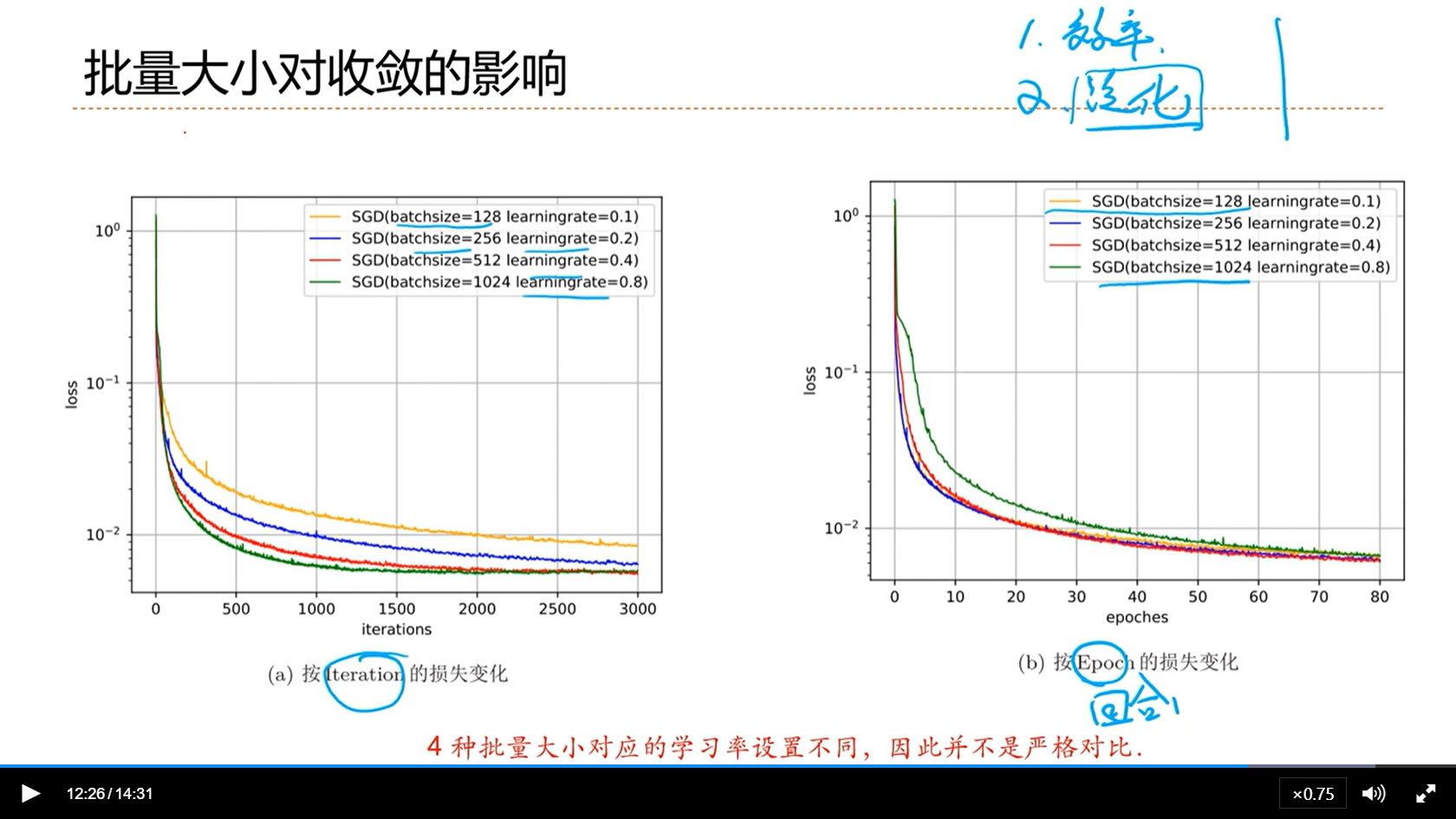
alec:
从作图可以看出,批量越大,越稳定,计算的方向越正确,下降的越明显。
批量的选择考虑:
- (1)效率角度:批量K尽可能的大,充分的利用GPU的算力
- (2)但是批量大的话,从优化的角度上讲,反而慢
- (3)泛化的角度:批量越小,随机性越强,因此这可能就起到了正则化的作用,从而使模型的泛华能力更好
批量具体选择多大,要看实验而定。总的来说,当训练样本非常多的时候,这个时候已经不用考虑过拟合问题了,因此这个时候批量越大越好。不需要考虑泛化问题。当样本量不是很大的时候,泛化性是比效率更重要的指标,这个时候批量大小就不用很大了。
[√] 如何改进?
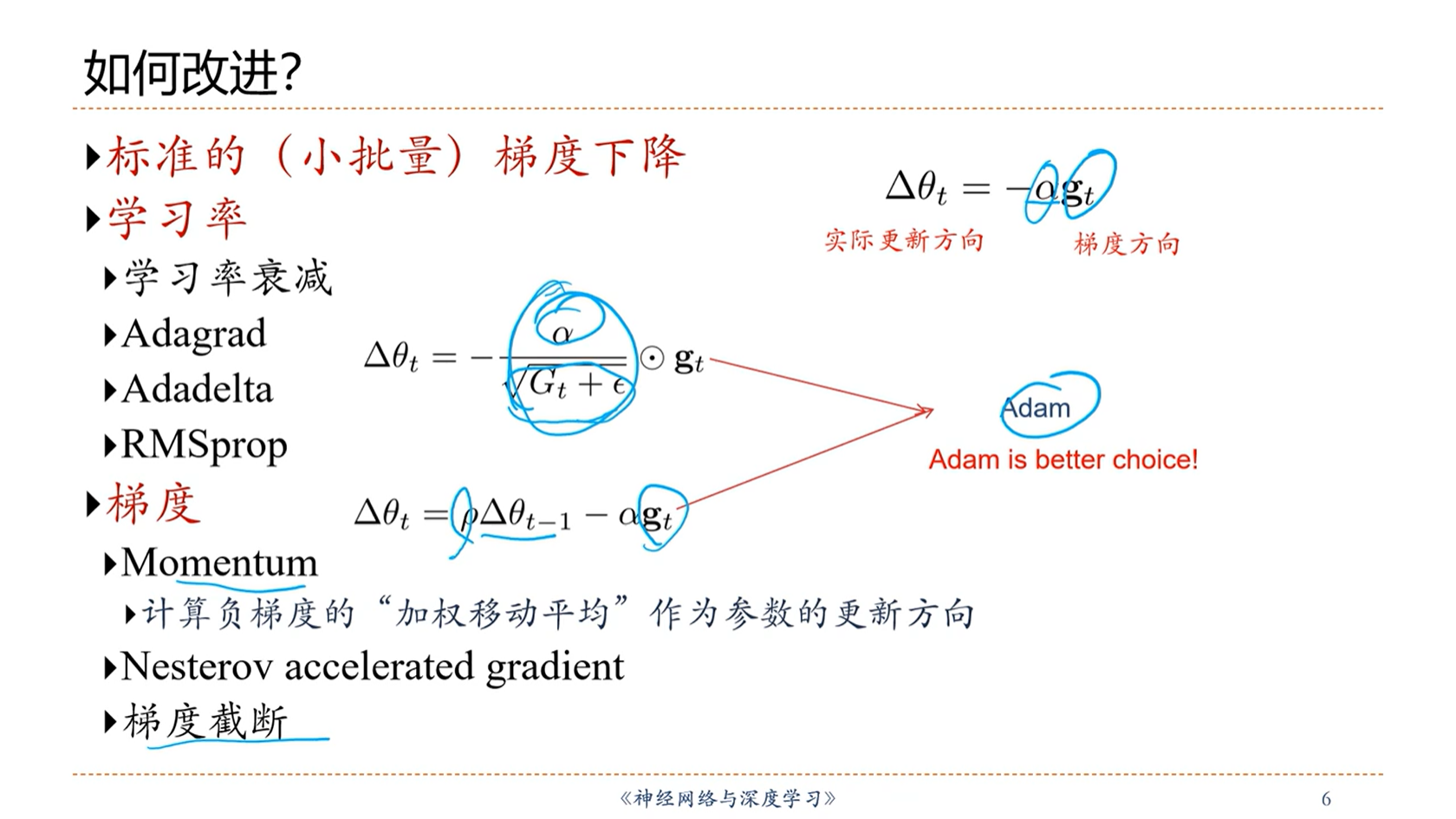
alec:
- adam算法,既是自适应学习率,也是考虑动量的方法。ada + m。
- 所以通常来讲,可以考虑默认使用adam作为优化算法,优化
学习率和梯度这两个点。
[√] 本节总结:
alec:
- 优化算法的考虑角度有三点:批量K、学习率α、梯度
- 批量K,数据量充分的时候,K尽可能大;数据量一般的时候,批量不要太大
- 综合学习率和梯度的是adam算法,学习率方法随着迭代次数的增多,学习率慢慢减小;且梯度是使用的移动加权平均,从而更加的稳定。
[√] 7.3 - 动态学习率
[√] 学习率的影响
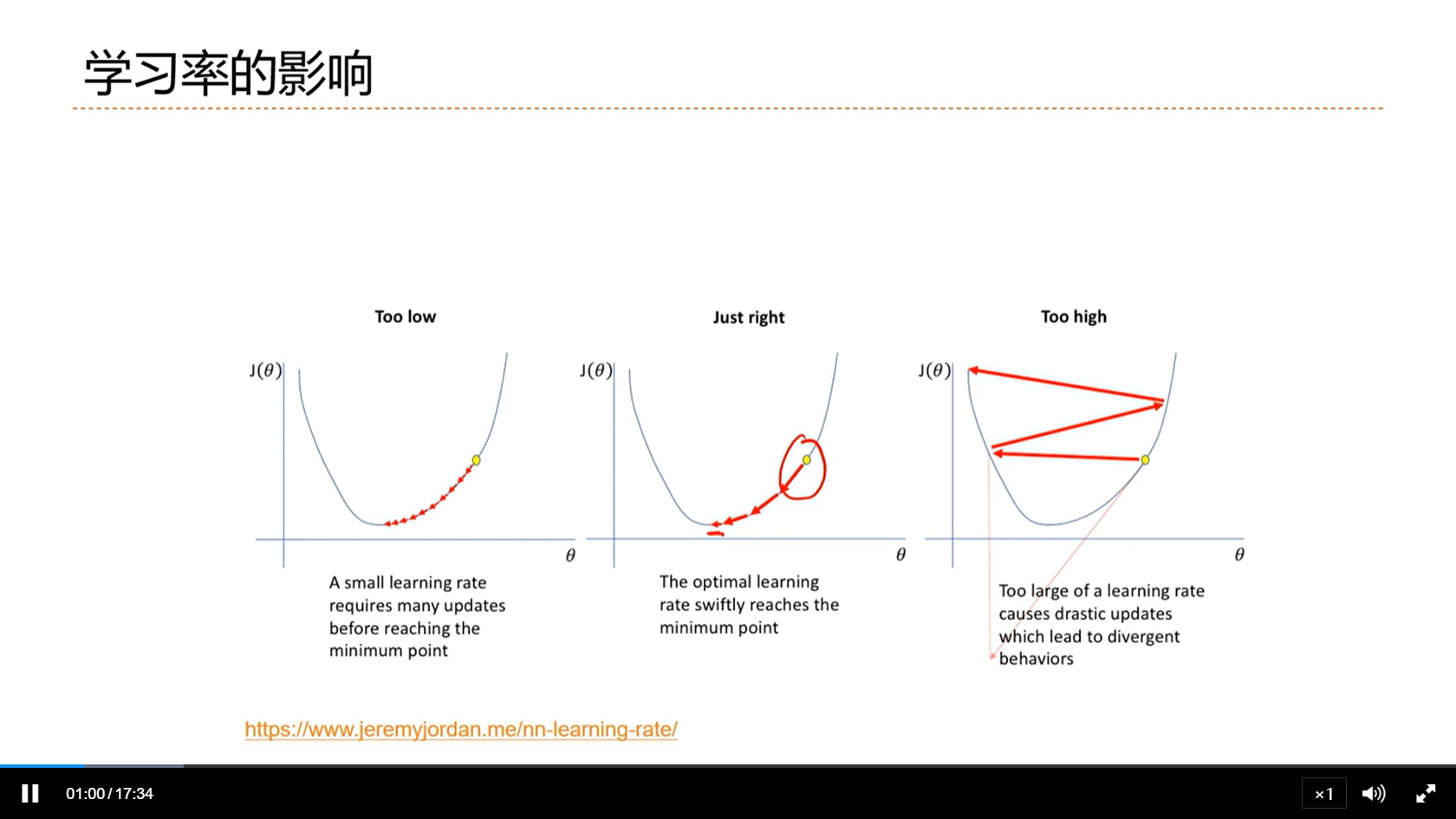
alec:
- (1)学习率太小,效率很低;学习率太大,步长太大,从而跳过最优点
- (2)学习率一般和批量K成正比
- 综合1、2,学习率设置要使用,批量也不能过大
- 一个好的学习率,通常是自适应的。
[√] 学习率衰减
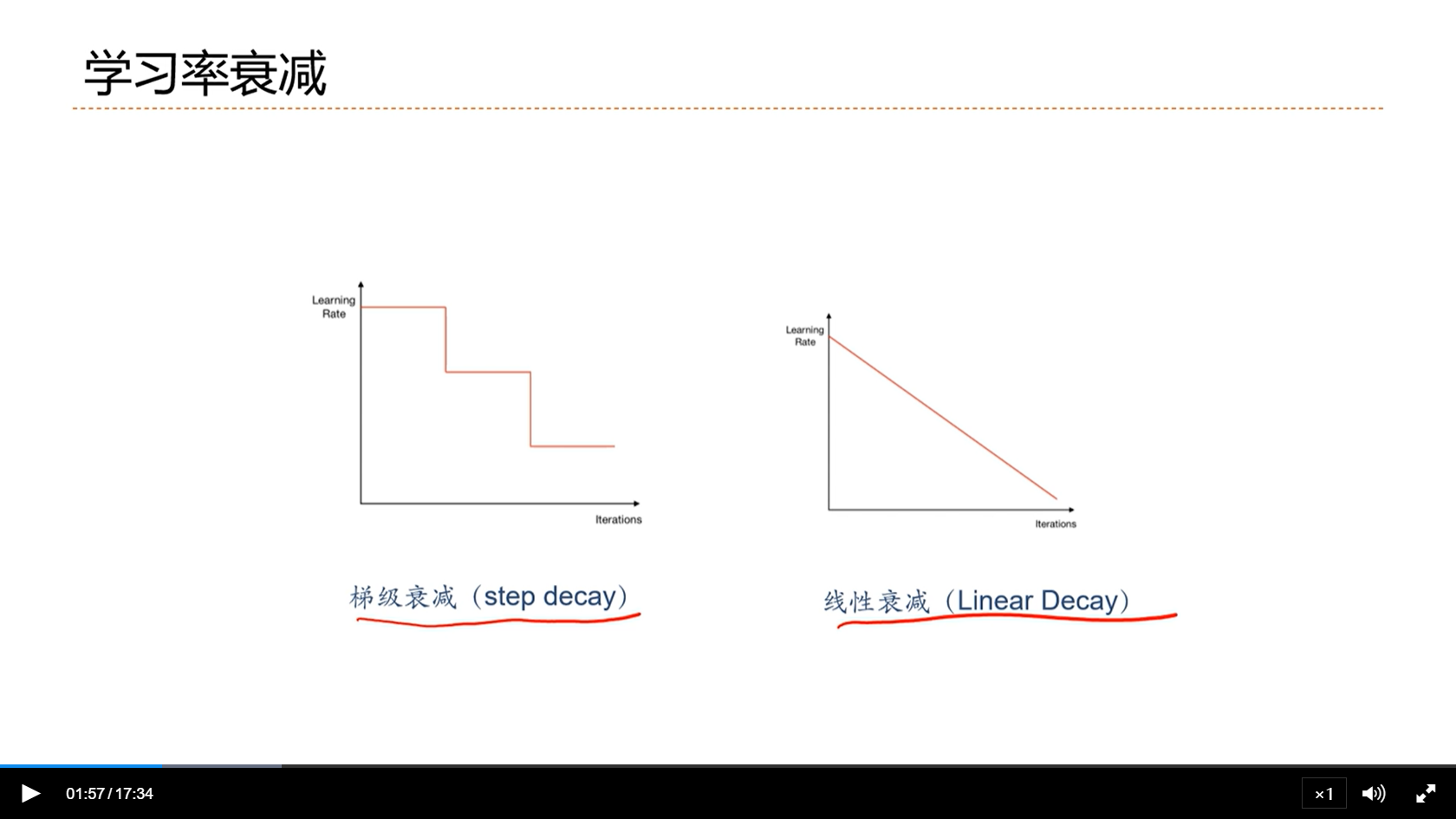

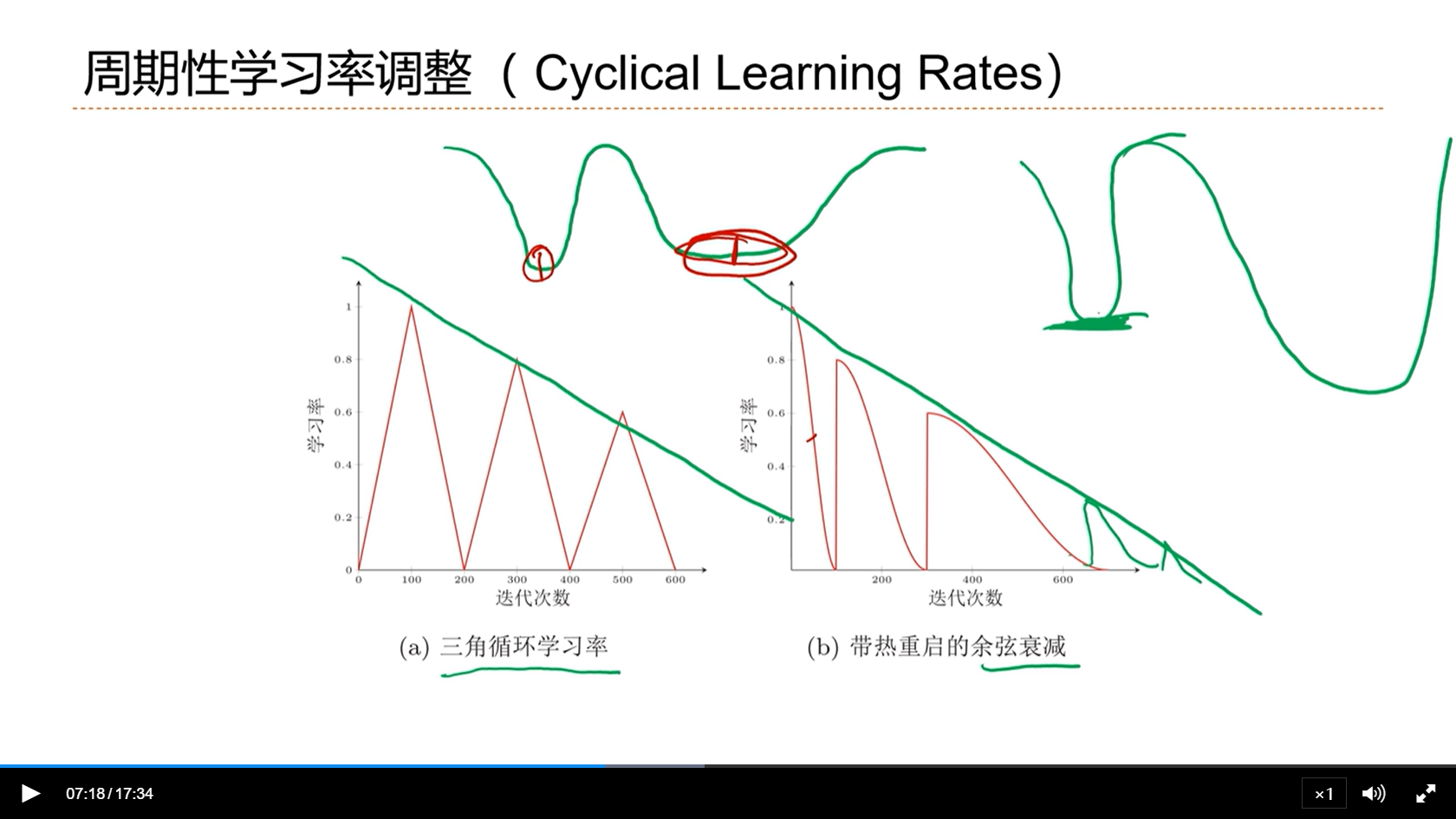
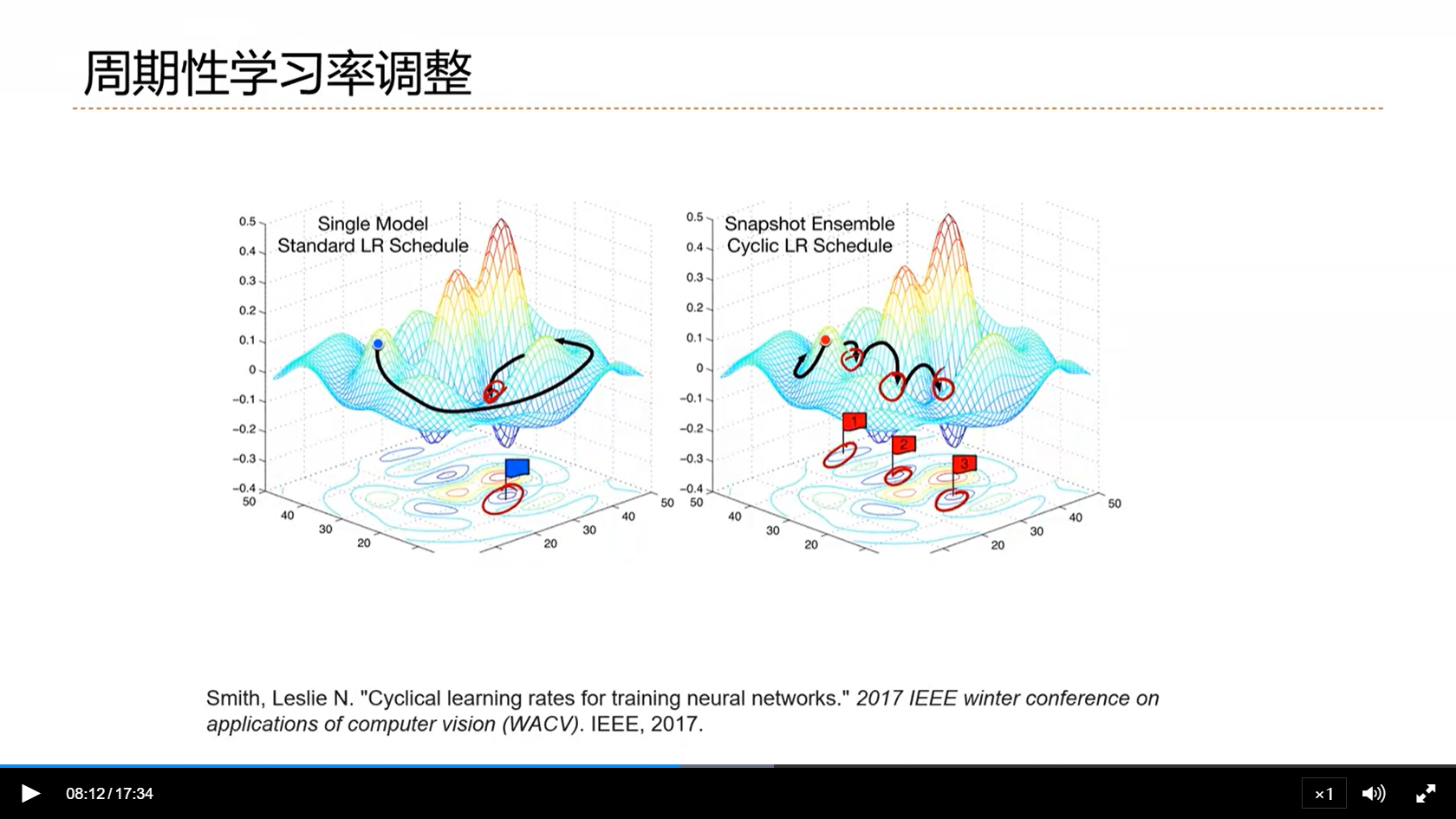
[√] 周期性学习率调整(Cyclical Learning Rates)
alec:
- 周期性的,不是一直递减的
- 为什么要做这种局部的衰减呢?
- 目的是为了跳出局部最优,或者是跳出鞍点,找到一个更好的局部最优解
- 通常来讲,会找到一个平坦的局部最优,从而提高模型的鲁棒性
- alec思考:周期性的调整学习率,不断地找局部最优,是否会错过最好的一个局部最优?
- 解决方法是,找到一个最好的局部最优,就保存此次的参数,在这种情况下,即使最后停留的位置不是最好的位置,也没关系。反而这种周期性的学习率,给了模型更多的机会去寻找更多的可能性。
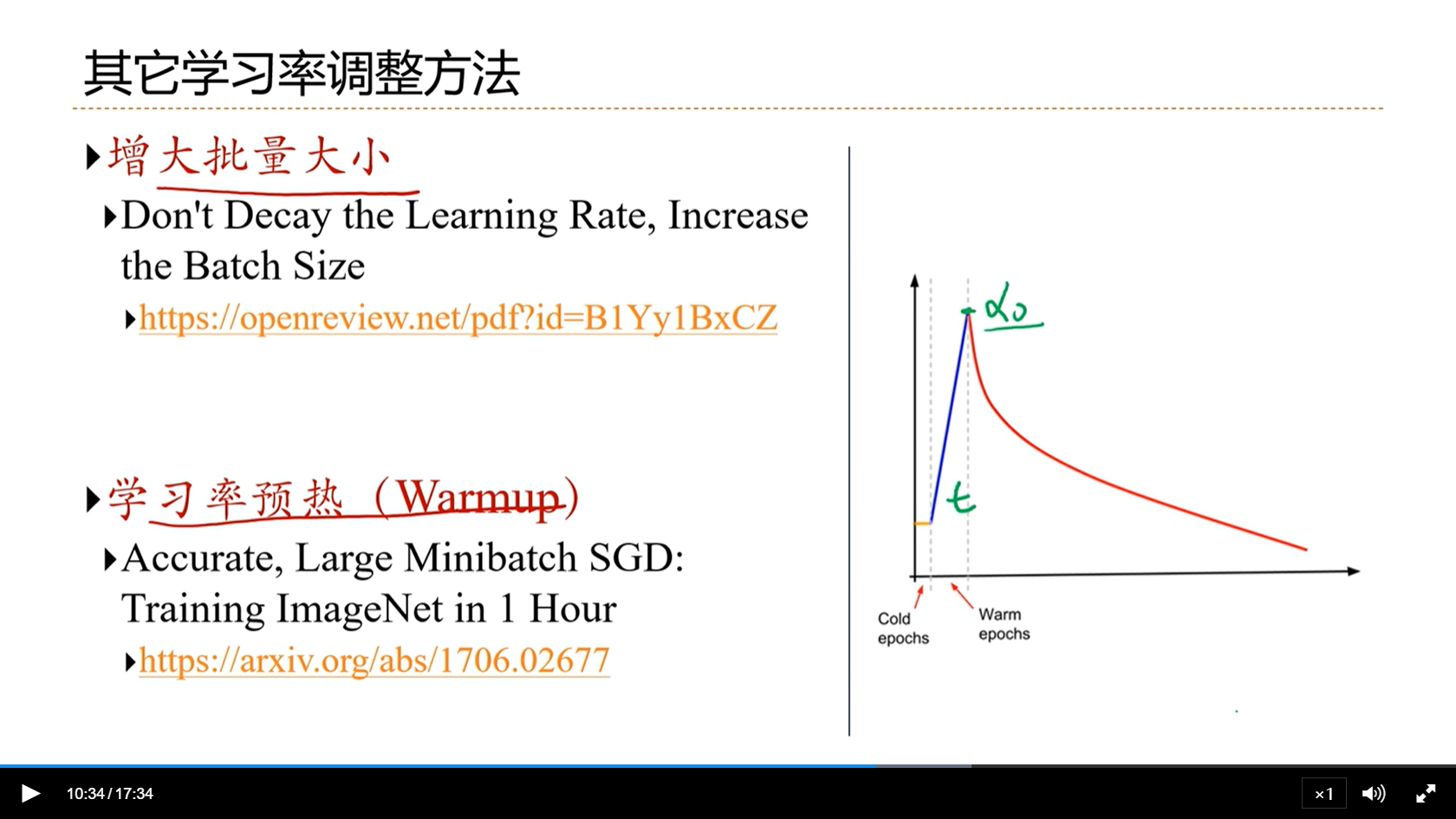
[√] 其它学习率调整方法
alec:
- 增大批量大小:一般来讲,学习率和批量大小成正比。当我们固定学习率,增大批量大小,其实就是变相的意味着减小了学习率。
- 学习率预热:这个目前已经成为训练神经网络的一个标配了。(alec mark)
- 一开始的时候,参数的初始值不一定是特别好,因此这个时候如果学习率也很大的话,那么可能就走的很乱。因此一开始的时候,可以让学习率小一点,慢慢预热,然后再减小。
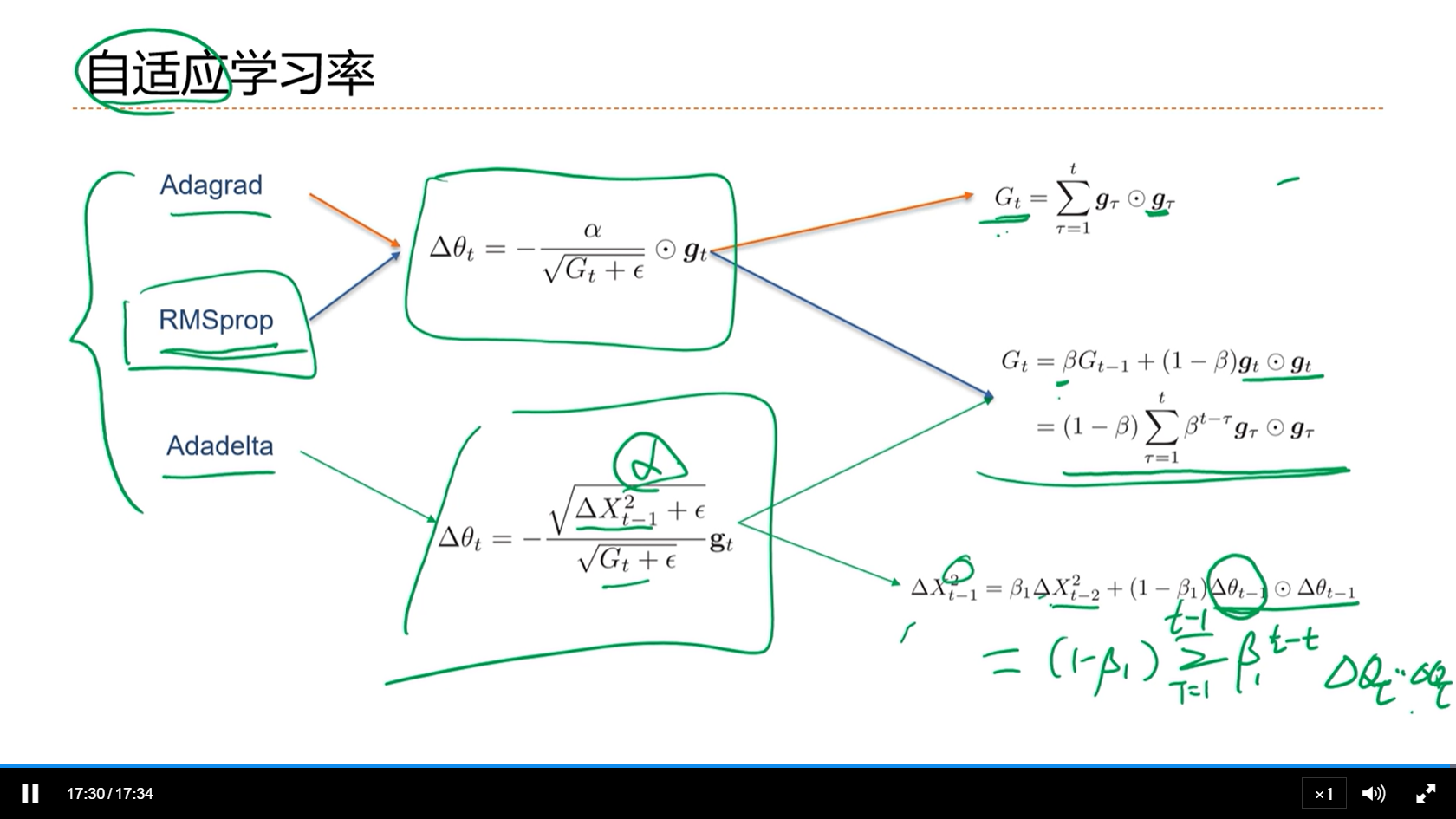
[√] 自适应的学习率
alec:
- AdaGrad中,分母是一直递增的,学习率是不断减小的
- RMSprop算法中,分母部分是移动平均,这样分母整体不是一直递增的,因此不会导致随着时间的推移梯度就消失了。这种方式从而就避免了AdaGrad的缺点
- Adadelta是对RMSprop的进一步改进。这种的好处是,分子中的α也是不固定的。当某个方向的梯度大的时候,这个学习率也大。梯度大意味着这个方向还没有学好,学习的不充分。因为学习率对应也大,这样学习的更加充分,从而收敛效率也更大
[√] 7.4 - 梯度估计修正
[√] 梯度估计修正
[√] 动量法(Momentum Method)
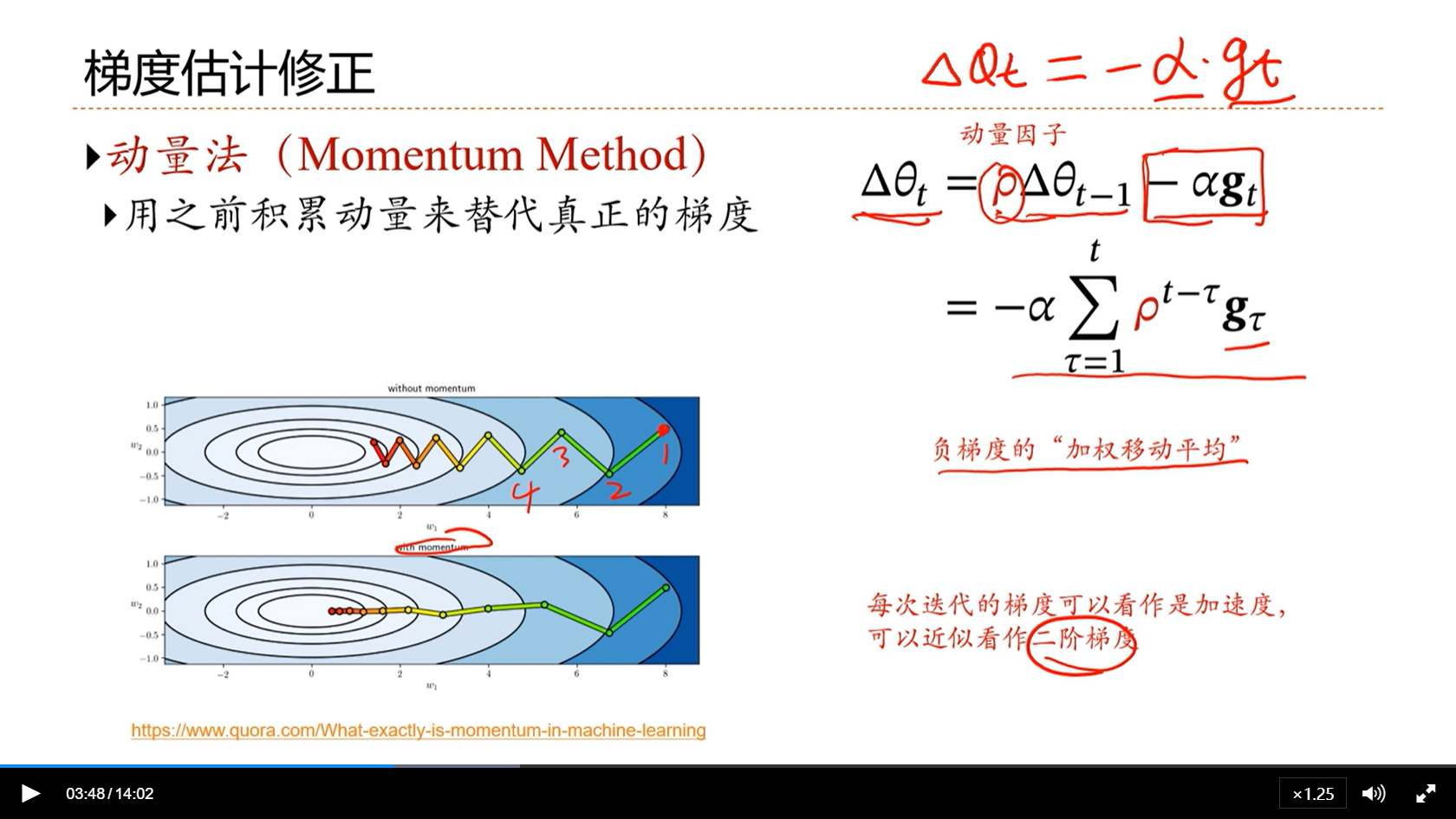
alec:
- 因为随机梯度下降的原因,每次的参数减去梯度,具有非常大的随机性。因此可以用之前累计的动量来代替真正的梯度。
[√] 梯度方向优化
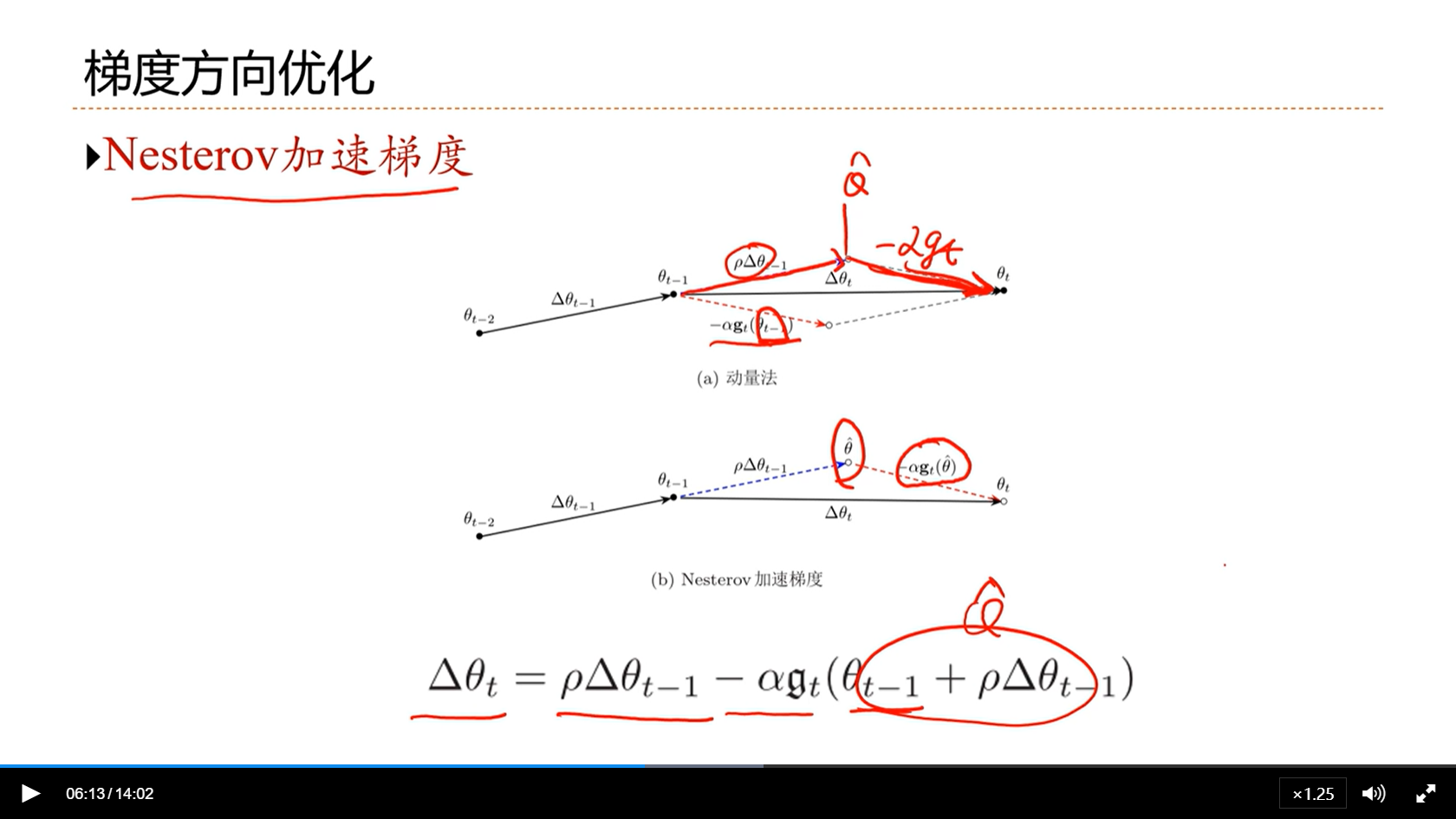
[√] 梯度方向优化+自适应学习率(adam优化算法)

alec:
- 为什么要修正?
- 因为当t=1的时候,M1 = (1-β)g1,这个时候的M1是不对的,因为梯度值实际上是g1,而不是(1-β)g1,所以t=1的时候,要给分母除以一个(1-β)。
- 使得在开头的几步,这个移动平均梯度估计的更准
[√] 优化
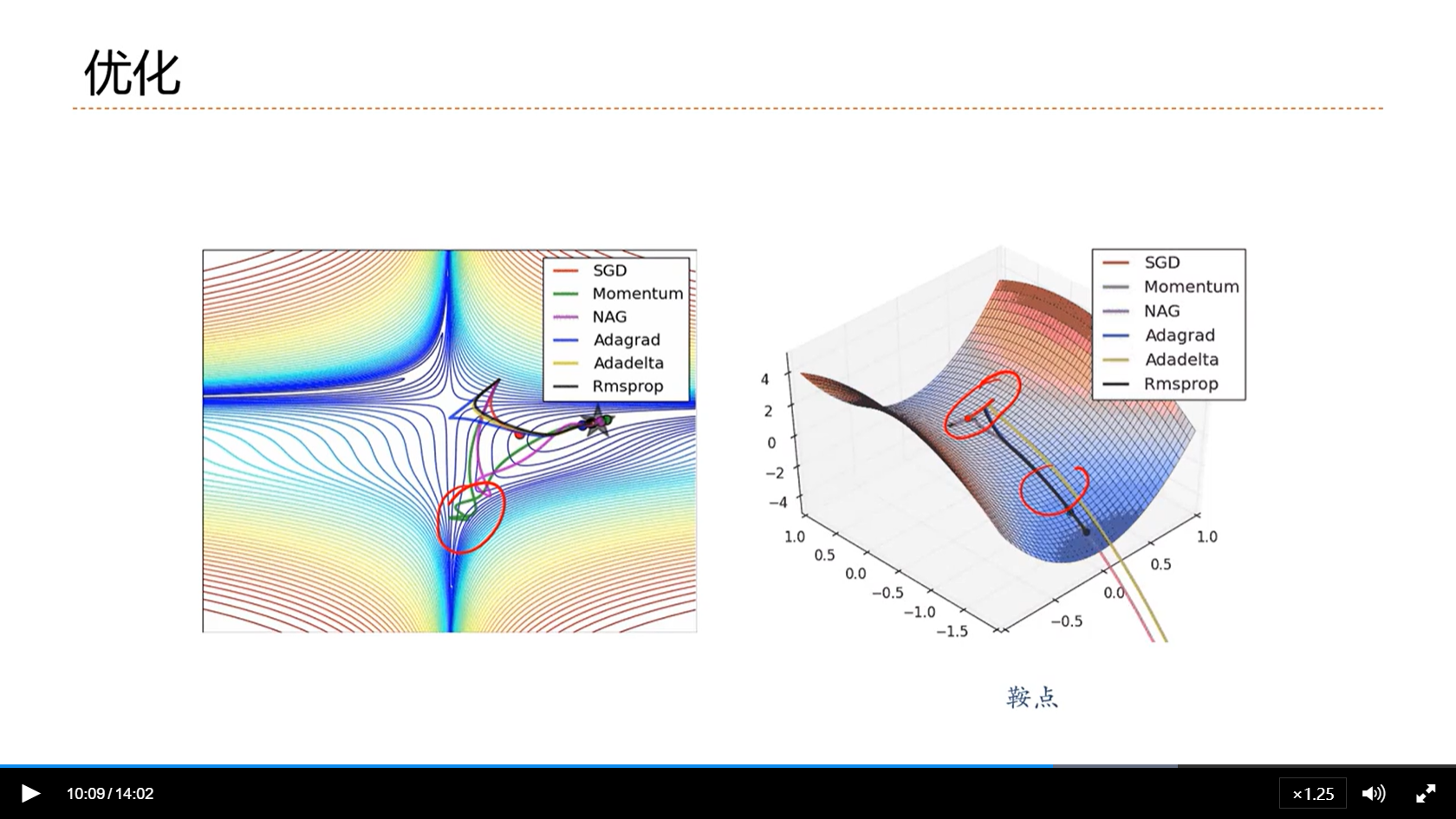
可以看出,带动量的,相对比较容易走出鞍点。
[√] 梯度截断
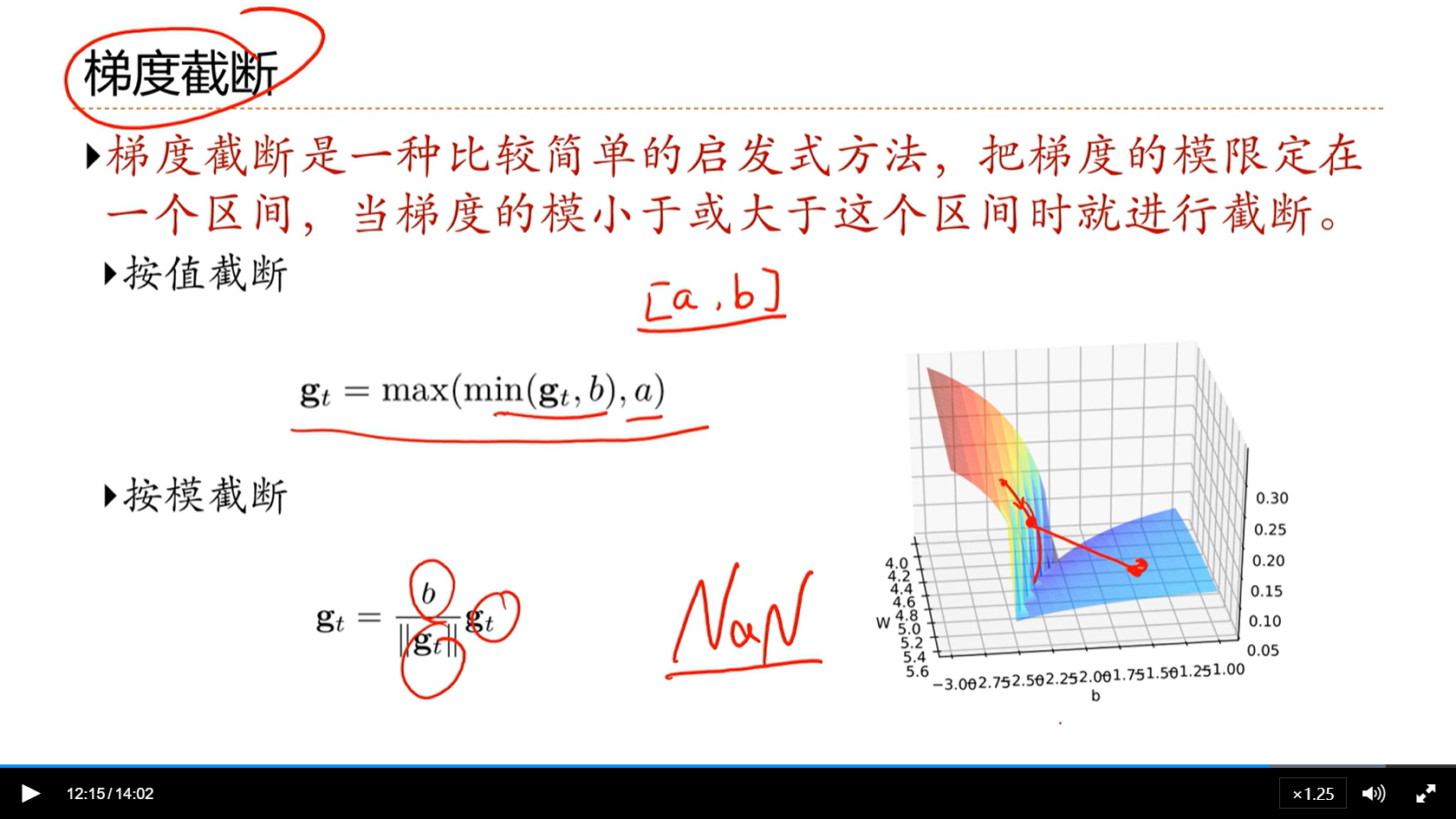
alec:
- 梯度太大了,容易跳过局部最优点
- 因此如果梯度太大了,就将梯度截断
[√] 优化算法改进小结
alec:
- 目前大部分能够用来优化神经网络的大部分算法↓

[√] 7.5 - 参数初始化
[√] 参数初始化
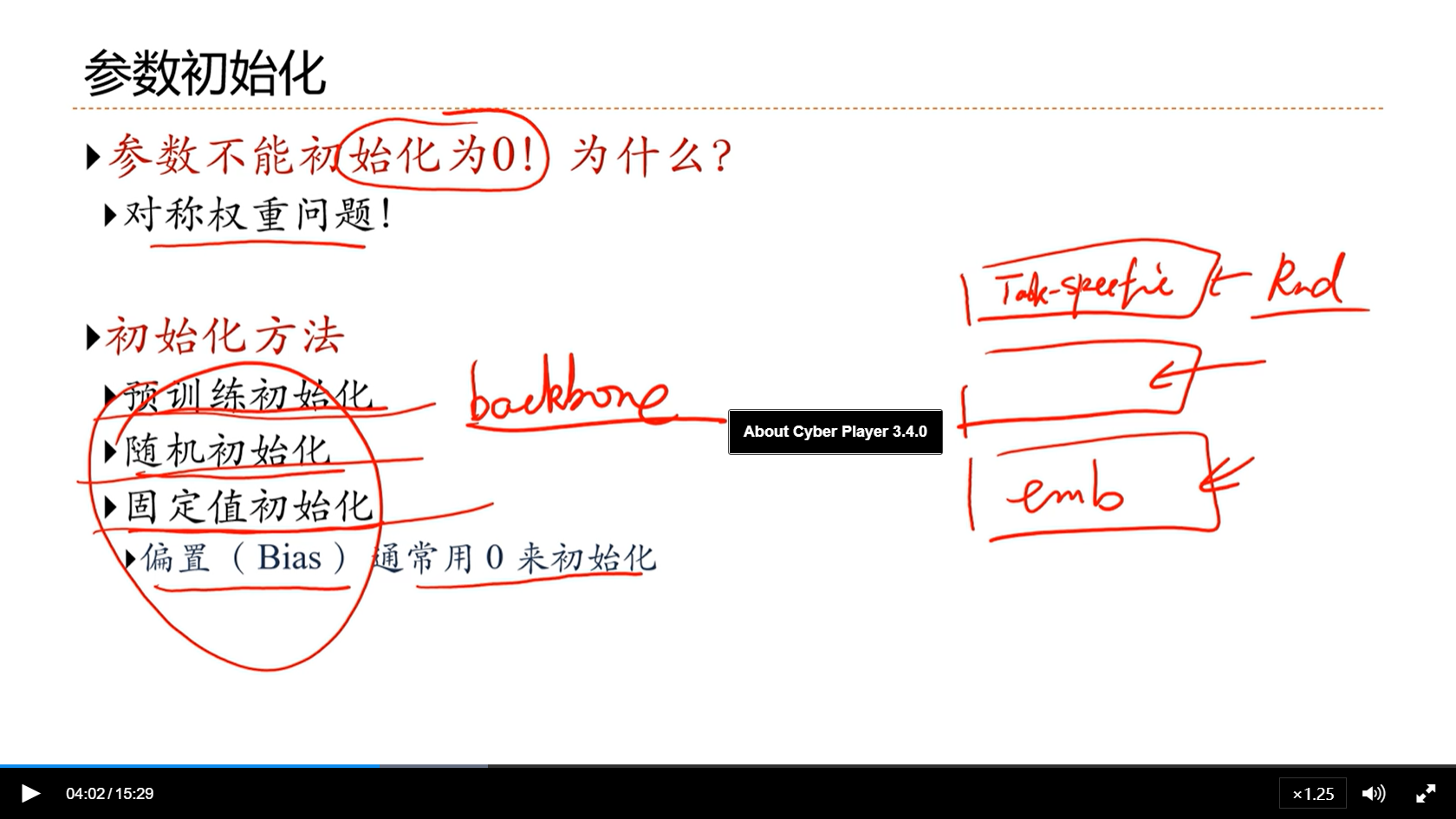
alec:
- 参数不能初始化为0
- 初始化方法中的预训练初始化,在预训练的网络上,在不同的下游微调就可以了。其中,预训练的网络,成为backbone
- backbone,脊柱、脊骨
固定值初始化
- 比如bias通常用0来初始化
- RNN中的,forget gate,通常让这个偏置大一点,让这个门一直打开
- 这三种初始化的方法,也可以混着用
- 特别是在NLP领域,很多的embedding通常都是预训练的,一些骨干网络可能也是预训练的,上面的一些任务特定层可能是随机初始化
[√] 随机初始化

alec:
- 问题:高斯分布的均值和方差是多少?均匀初始化,那么r是多少?
- 比如,不能用很大的初始值,比如如果很大的话,我们使用饱和性的激活函数,数值很大的话,激活函数立马就饱和了
- 例如可以根据所用的激活函数,让初始化之后,线性部分的取值在激活函数的线性部分
[√] 范数保持性
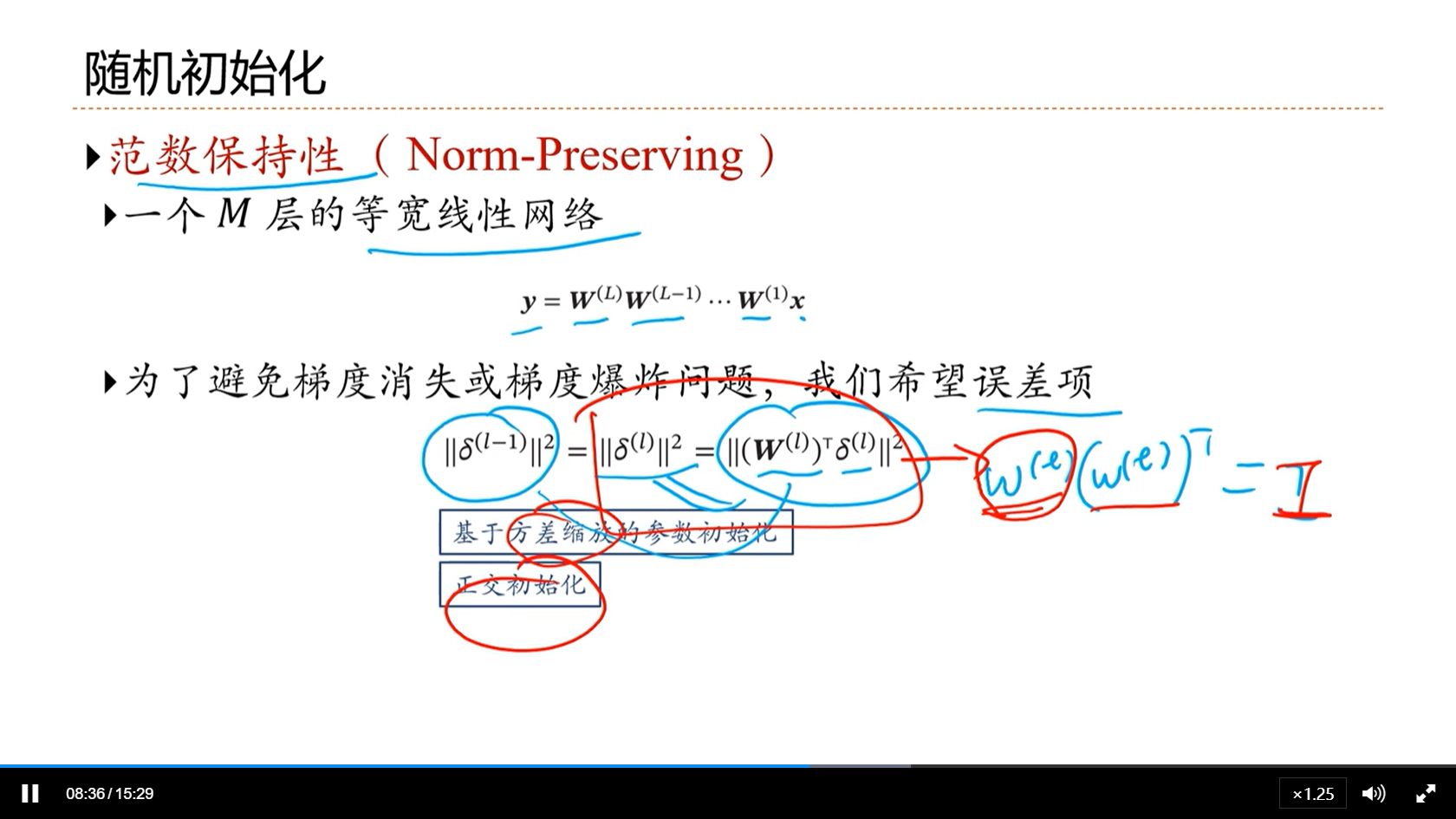
alec:
- 我们希望在参数初始化的时候,最终参数W的范数,能够是单位阵。
- 实现上述的方法可以是:(1)基于方差缩放的参数初始化(2)正交初始化
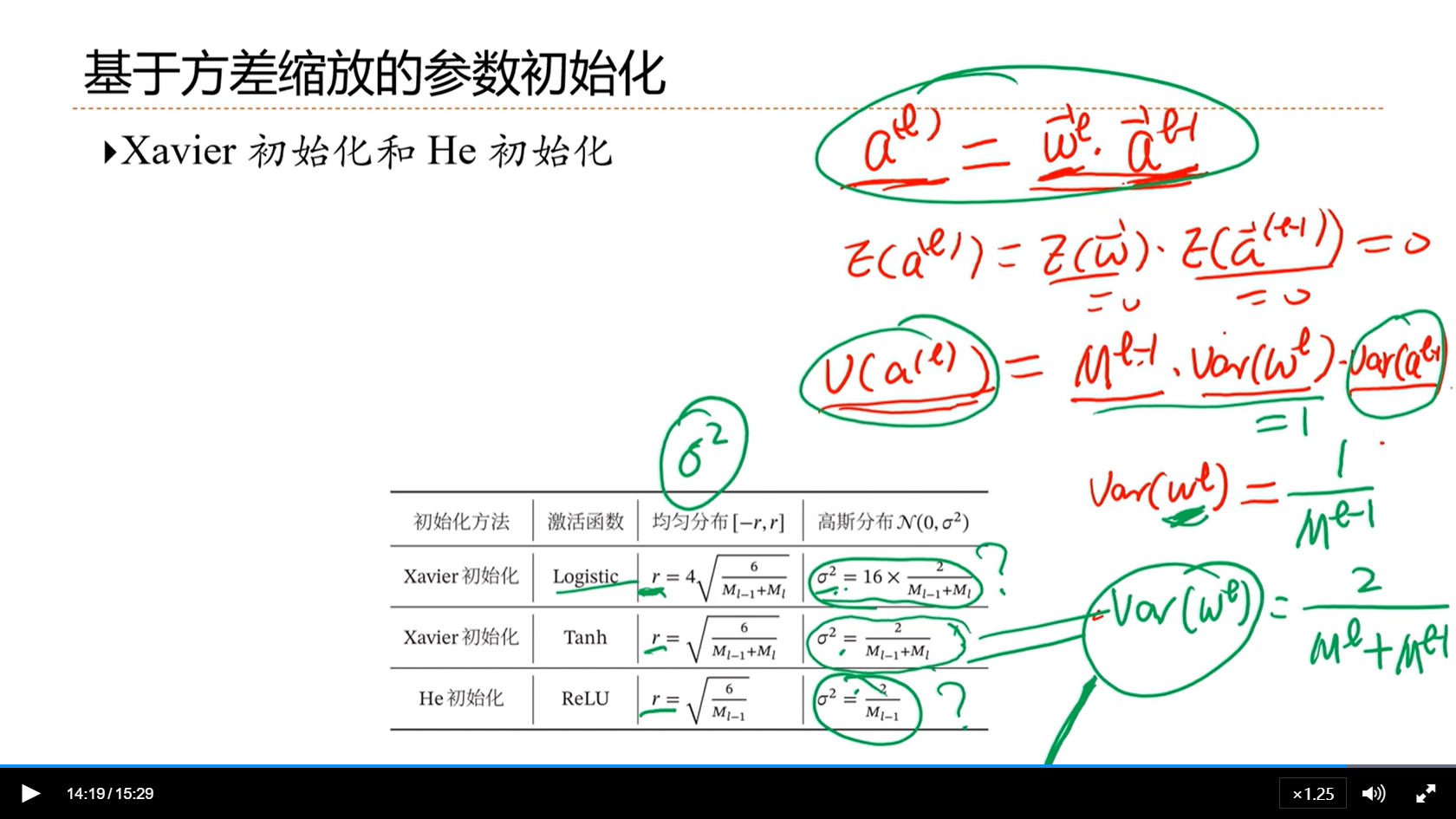
[√] 基于方差缩放的参数初始化
alec:
- 我们希望在方差缩放初始化之后,整个网络的神经元的活性值保持一致,从而让梯度不会消失或者爆炸

alec:
- 如上图,通过推导,我们希望第L层的参数的方差,等于1/M^l-1^
- 其中,M为第L-1层的神经元的数量
- 通过上述的推导,我们知道第L层的参数初始化的均值和方差能够通过第L-1层的神经元数量退出来
- 每层的初始化参数W的方法能够知道,跟随者每个上一层的神经元数量变化,因为这种参数初始化的方法叫做基于方差缩放的参数初始化。这种参数初始化的最终目的是希望不会产生梯度消失或者梯度爆炸问题
[√] 正交初始化
正交初始化的方法:

alec:
- 正交初始化通常用在循环神经网络中,用在RNN的hidden state到hidden state。因为RNN要不断的迭代,很容易发生梯度爆炸或者梯度消失问题。

[√] 7.6 - 数据预处理和逐层规范化
alec:
- 参数初始化,是对每一层的参数做处理,从而使得网络的性能更优
- 逐层规范化,是对神经元的值进行处理,从而使得网络的性能更优
- 数据预处理的依据有尺度不变性
[√] 尺度不变性(Scale Invariance)
[√] 尺度不变性
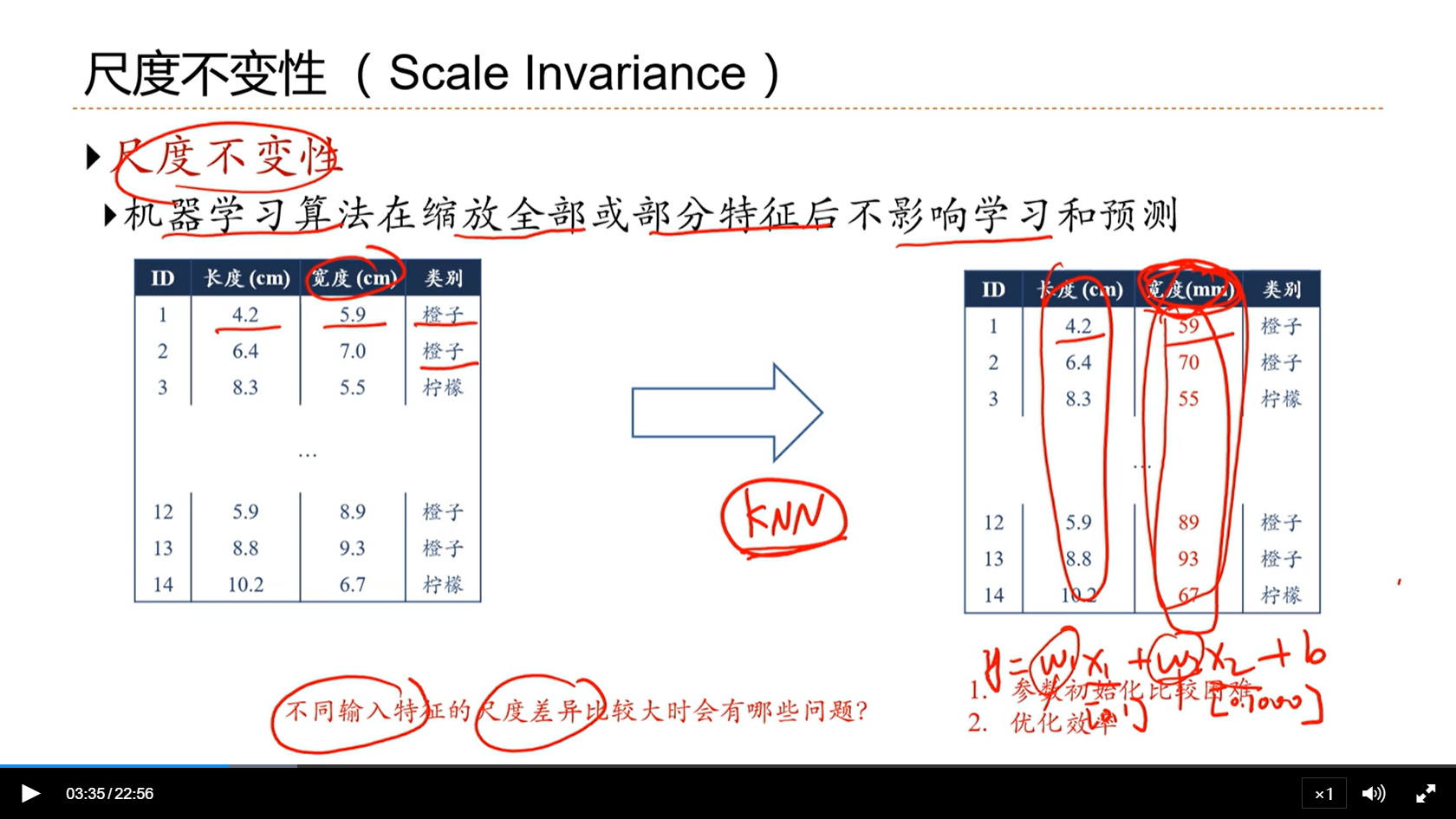
alec:
- 有些方法,具有尺度不变性
- 有些不可以,比如KNN最近邻分类器
- 不同输入特征的尺度差异比较大时会有哪些问题?
- (1)参数初始化的问题
- (2)也会对优化产生影响
[√] 数据规范化对梯度的影响
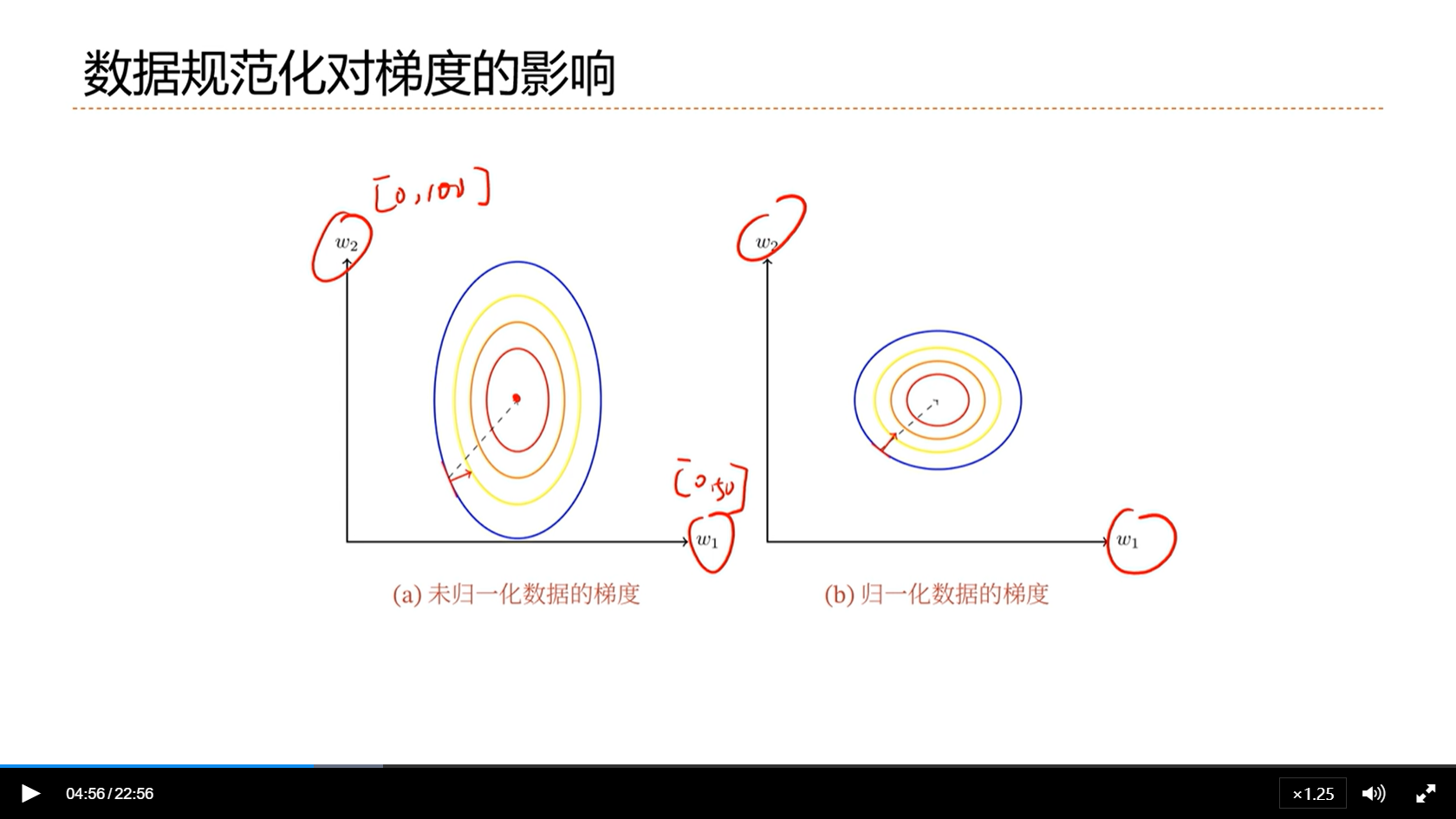
alec:
- 规范的数据,更加有利于训练
[√] 规范化(Normalization)
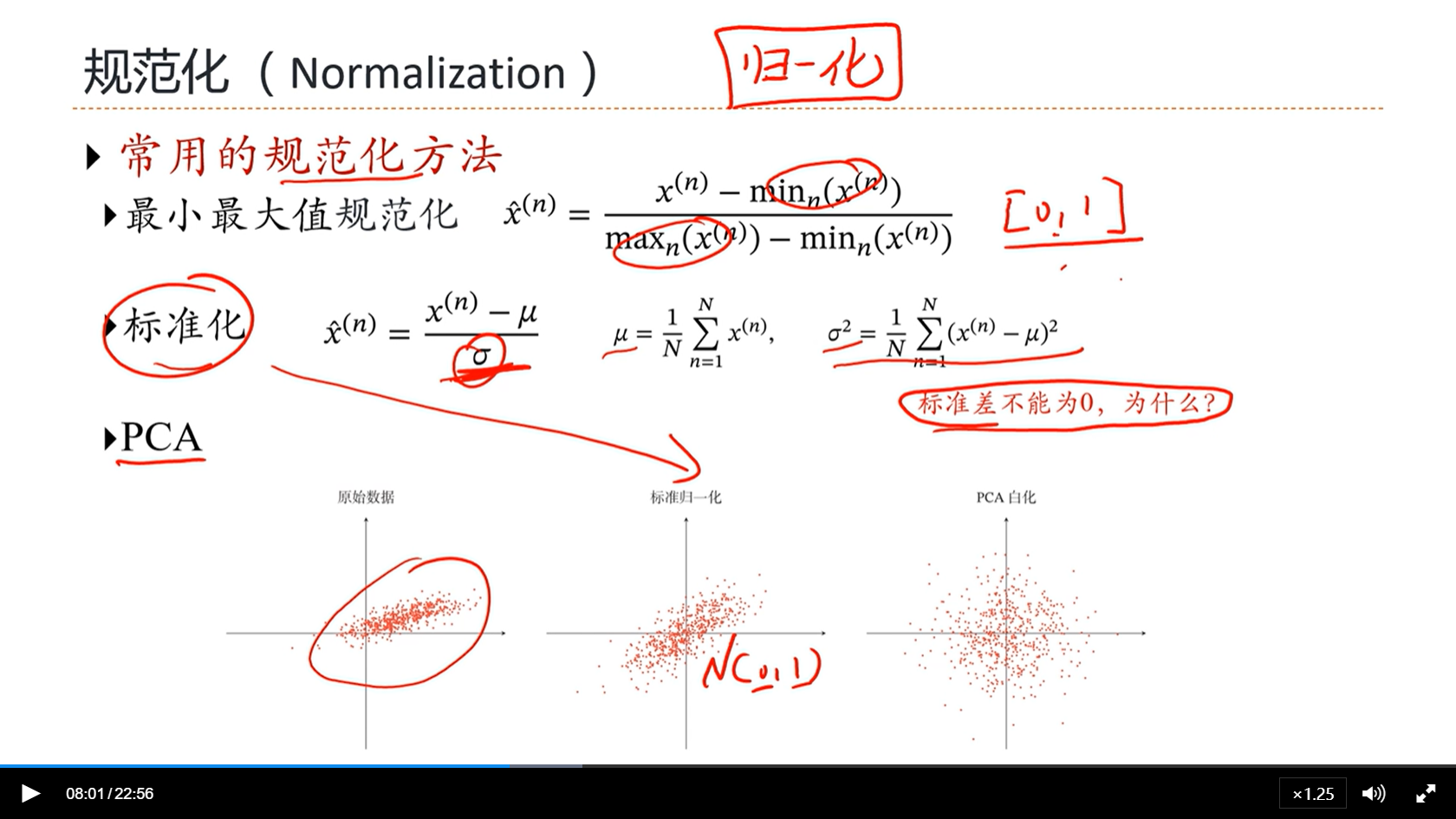
alec:
- 规范化也叫归一化
- PCA方法,把不同特征之间的相关性也去掉,这是一种更好的数据规范化方法
- 但是因为PCA的计算复杂度通常比较高,因此在实际的应用中,我们通常用标准化方法更多,标准化方法就够了。
[√] 7.7 - 逐层规范化
[√] 逐层规范化

alec:
- 逐层规范化,是目前在神经网络中或者深层神经网络中非常流行的方法
- 既然规范化具有好的作用,因此我们可以把这种方法应用到每一层,这种叫逐层规范化
- 我们希望第L-1层的输出的激活后的神经元的值,送到第L层,也是规范化的
- 也不一定每一层都规范化,也可以每间隔几层规范化
什么叫协变量偏移?
- 机器学习的前提是数据都是满足独立同分布的
- 如果数据不一致的话,就产生了协变量偏移,也就是说中间每一层的激活值,随着参数的变化,激活值的分布会变化。
- 通过逐层规范化,可以让数据分布保持不变
- 比如迁移学习,就是解决协变量偏移问题
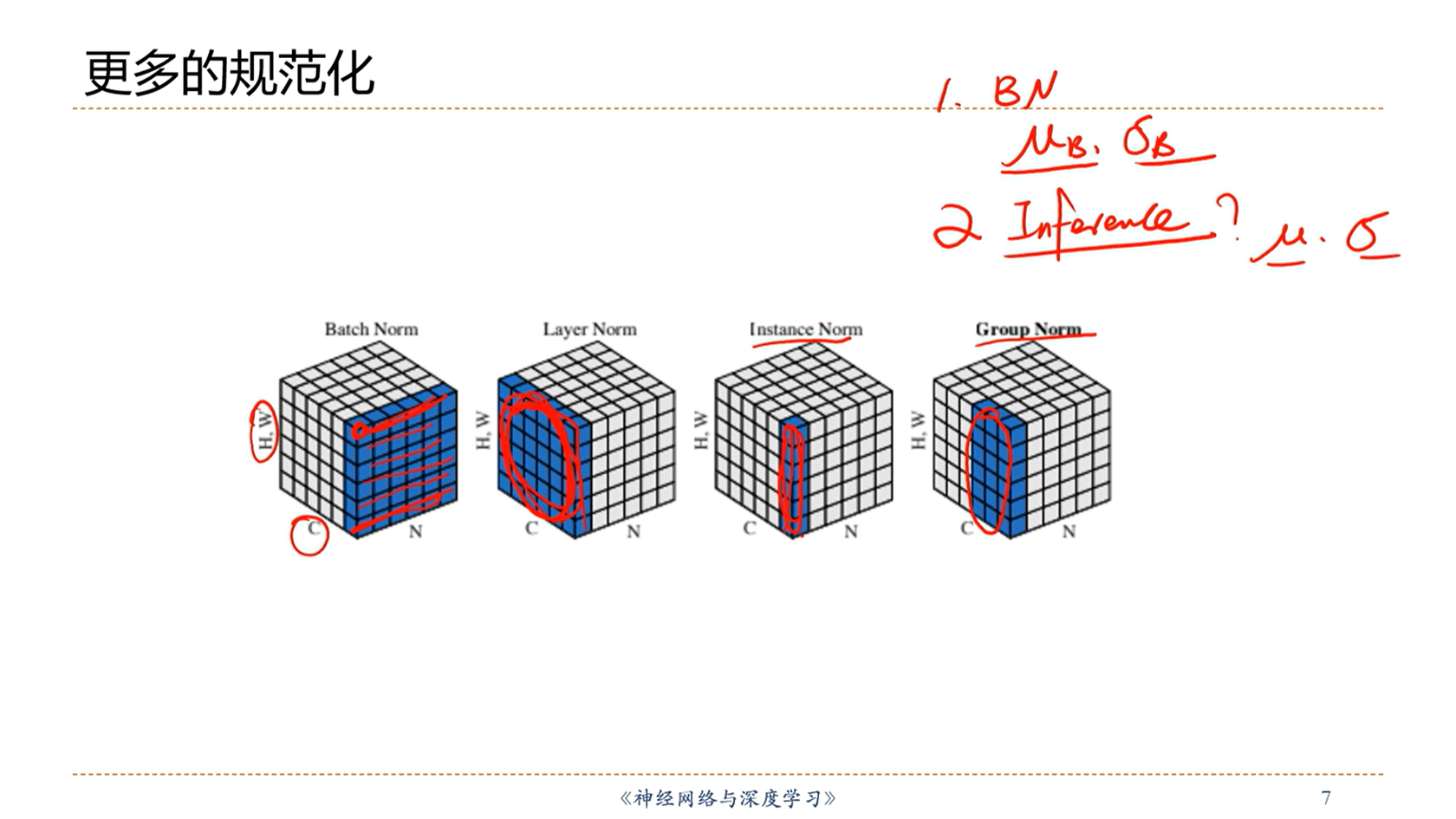
其中,BN-批量规范化,是比较常用的规范化
[√] 批量规范化

alec:
- BN就是在每层中,对一个批次的数据计算均值和方差
- 注意,BN计算的是在计算出线性值Z之后,进入激活层计算激活值a之前的均值和方差,然后对Z进行BN
- 计算出均值和方差之后,让所有的Z减去均值,除以方差。同时为了稳定,在分母加入保护参数。同时对数据进行缩放和平移,避免数据都挤在零值附近,从而无法利用激活函数的非线性。
- 通过BN中的缩放和平移操作,就能看出我们是在进入激活层之前进行BN的。
- γ和β都是可学习的参数
- 这个BN可以作为NN的一层,直接接到NN中
[√] 批量规范化的优缺点

alec:
- 缺点:
- 使用BN的时候,B的大小不能太小,否则就没有统计意义了
- 不能用到RNN
[√] 层规范化

alec:
- 注意区分逐层规范化和层规范化
- BN是在单个神经元上对一个batch的数据进行规范化
- 层规范化是对单个数据,一层的全部神经元进行规范化,全部神经元表示数据的不同的特征
[√] 批量规范化VS层规范化
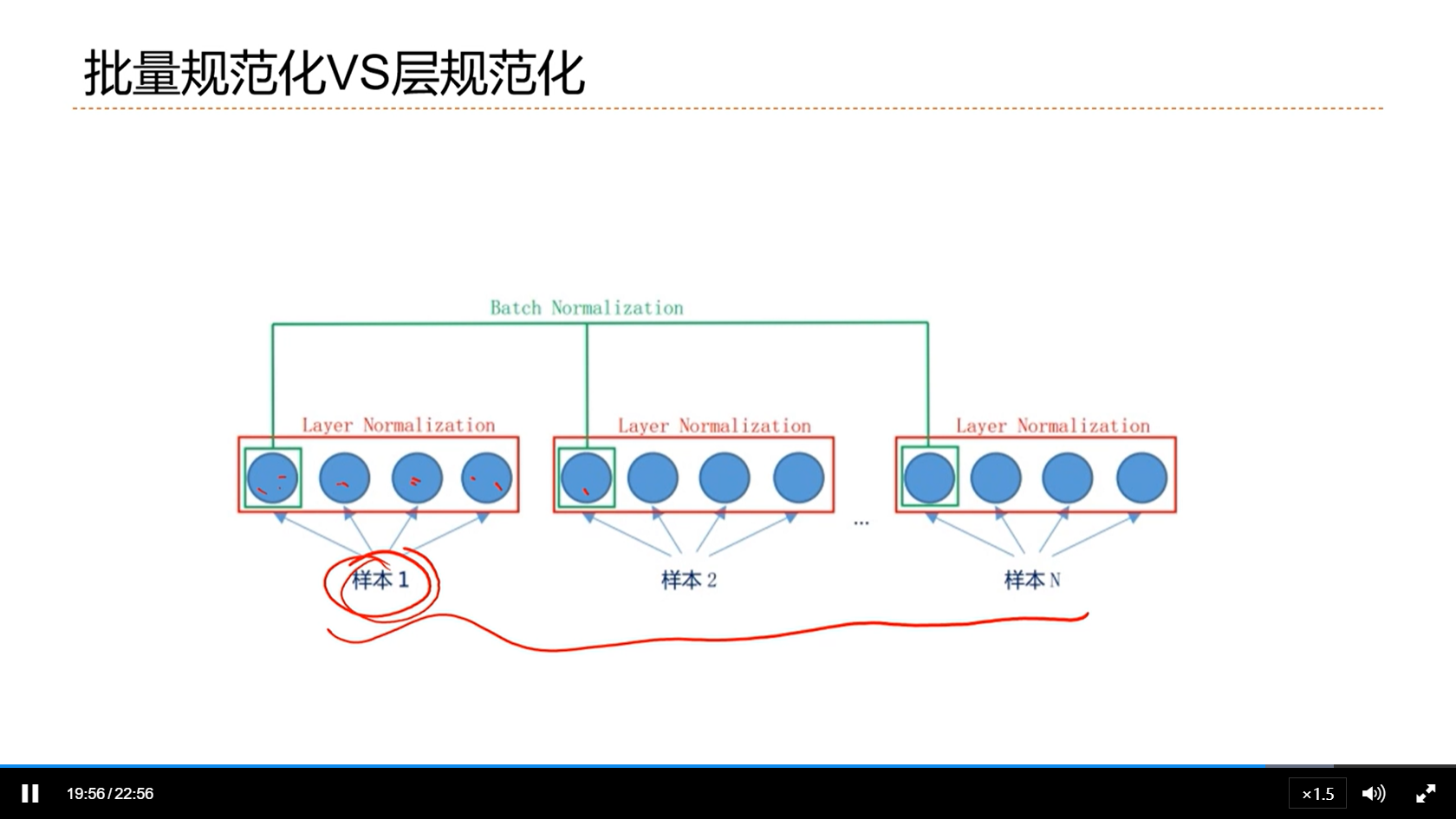
二者效果类似
在CV上,CNN方面,用BN多一点;但是总体来说,用层归一化用的更多
[√] 更多的规范化
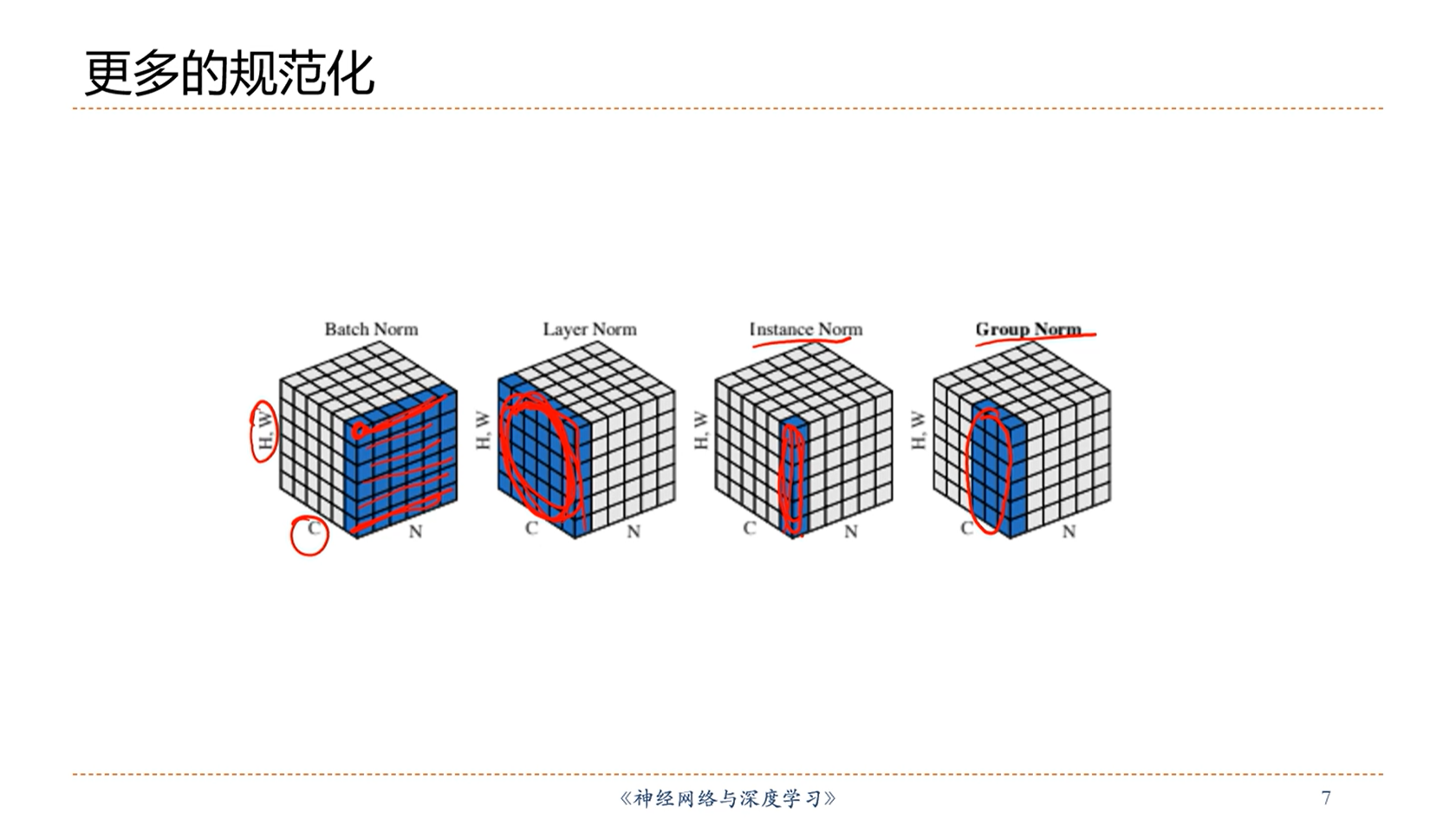
alec:
- 问题:
- 训练的时候,均值和方差能够计算
- 在测试的时候,均值和方差怎么拿到?
[√] 7.8 - 超参数优化
[√] 超参数优化

alec:
- 在训练之前,需要实现确定的参数叫超参数
- 这些超参数无法学习得到,必须通过经验来调整
[√] 网格搜索(Grid Search)

alec:
- 网格搜索,就是所有的超参数,对每个超参数根据经验确定几个取值,然后排序排列组合一个个试试
[√] 随机搜索
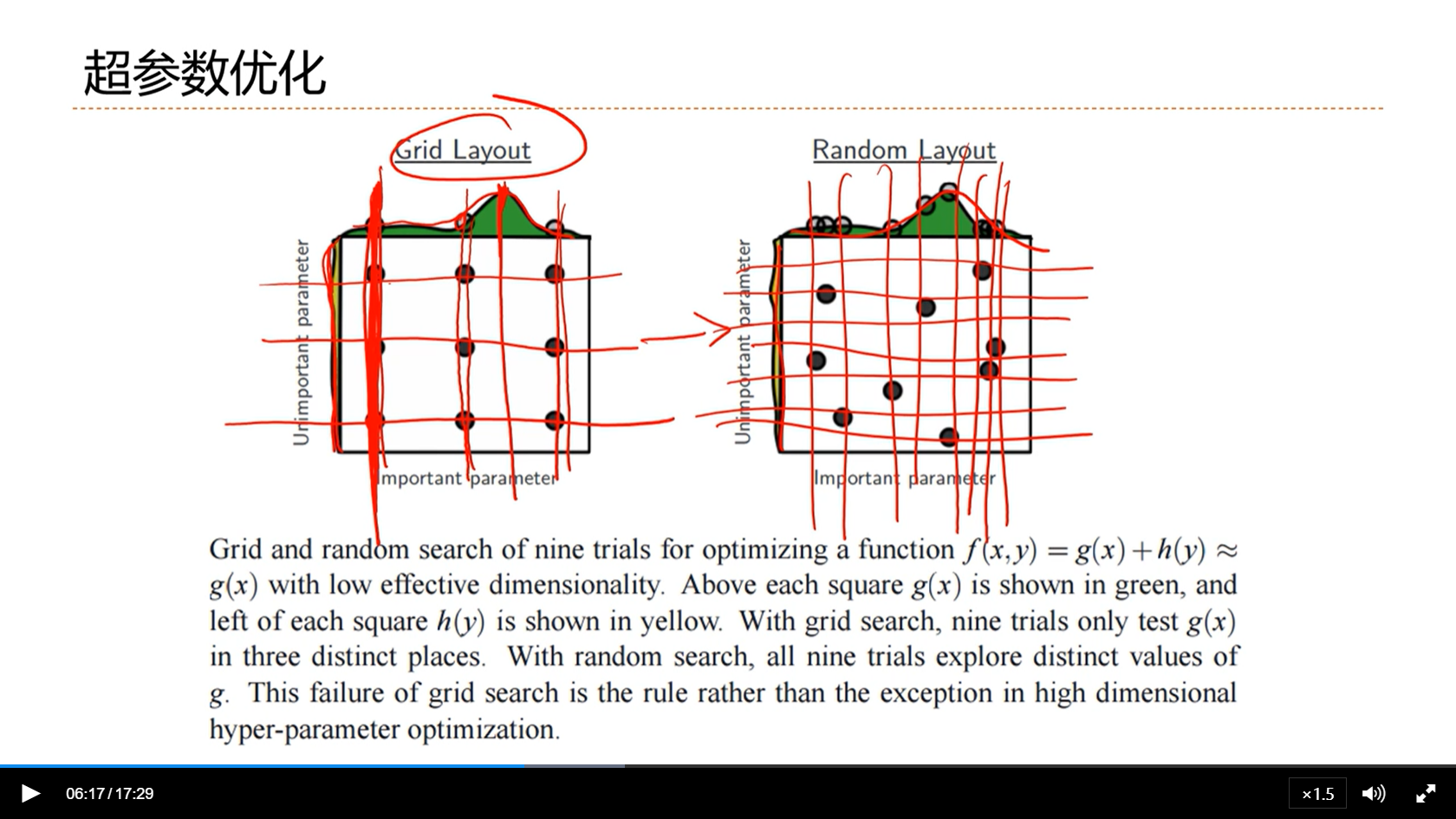
alec:
- 有些时候,有些参数的重要性比较大
- 改进方法就是每个参数的取值都是随机取的
[√] 一些高级的超参数优化方法
[√] 7.9 - 网络正则化
alec:
- 网络的正则化指的是对网络的能力进行限制,防止网络过拟合训练集
- generalization是泛化、normalization是标准化、归一化
[√] 重新思考泛化性
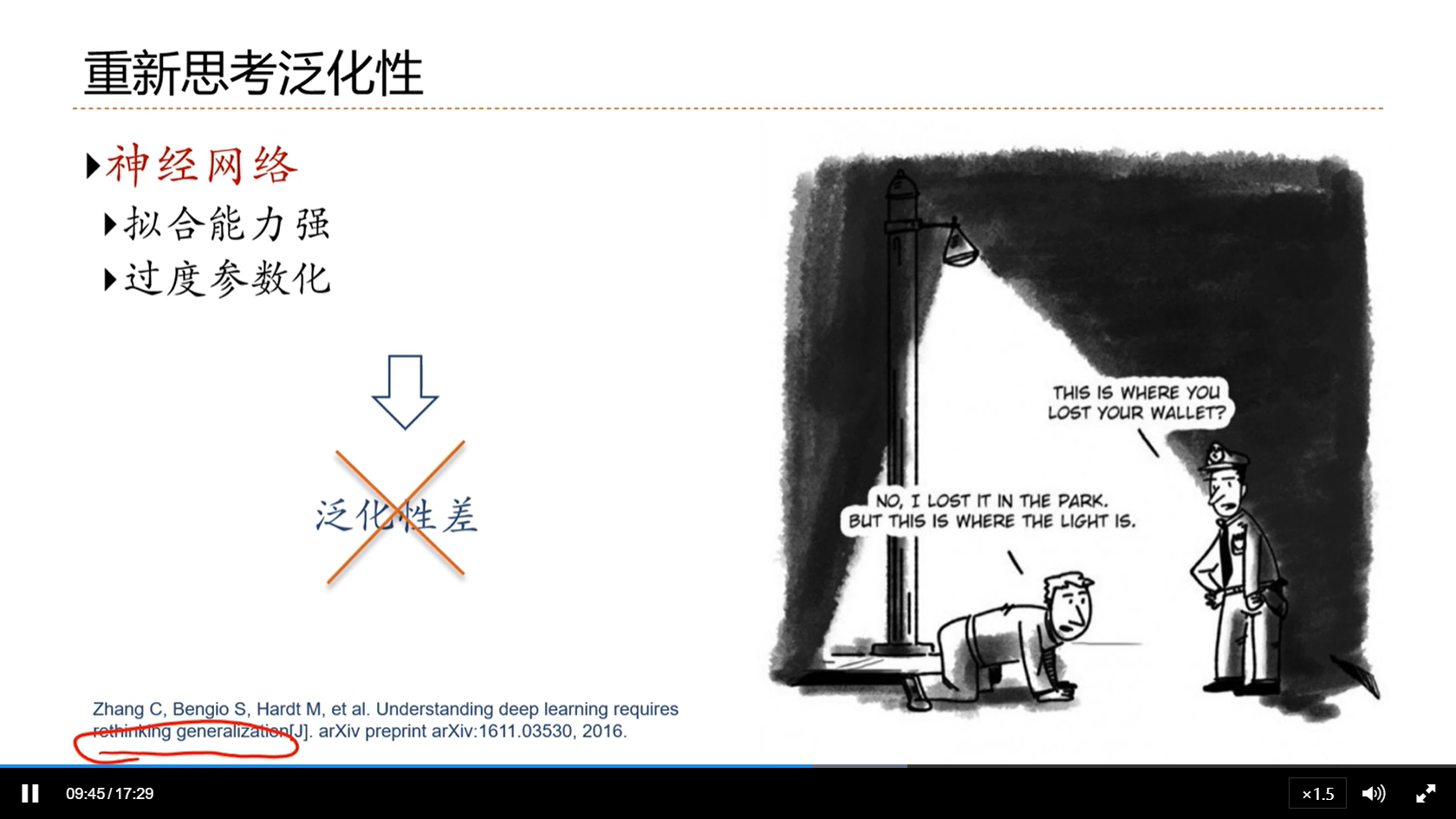
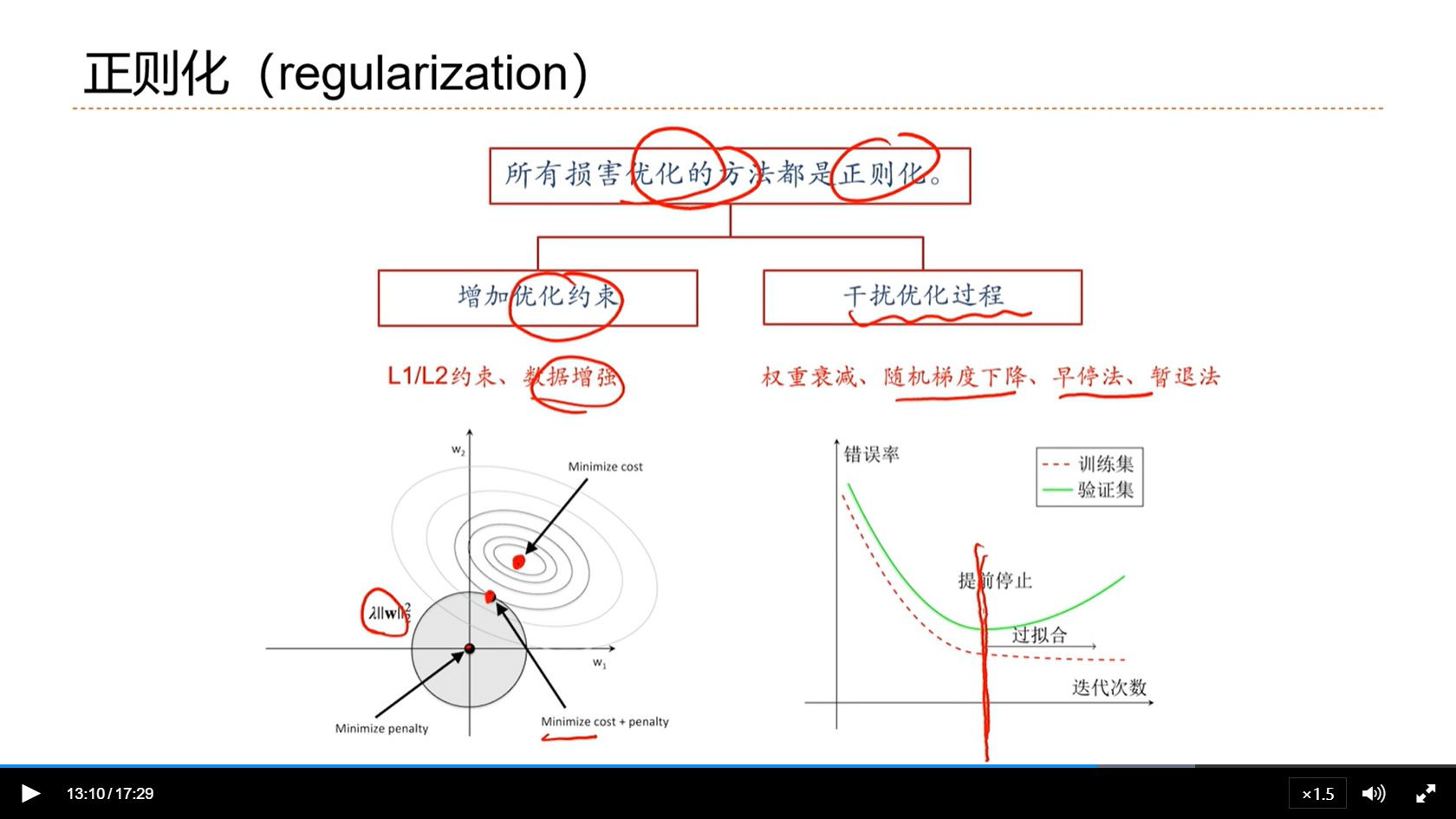
[√] 正则化(regularization)
alec:
- 所有损害优化的方法都是正则化。

[√] 早停法(Eary-Stop)
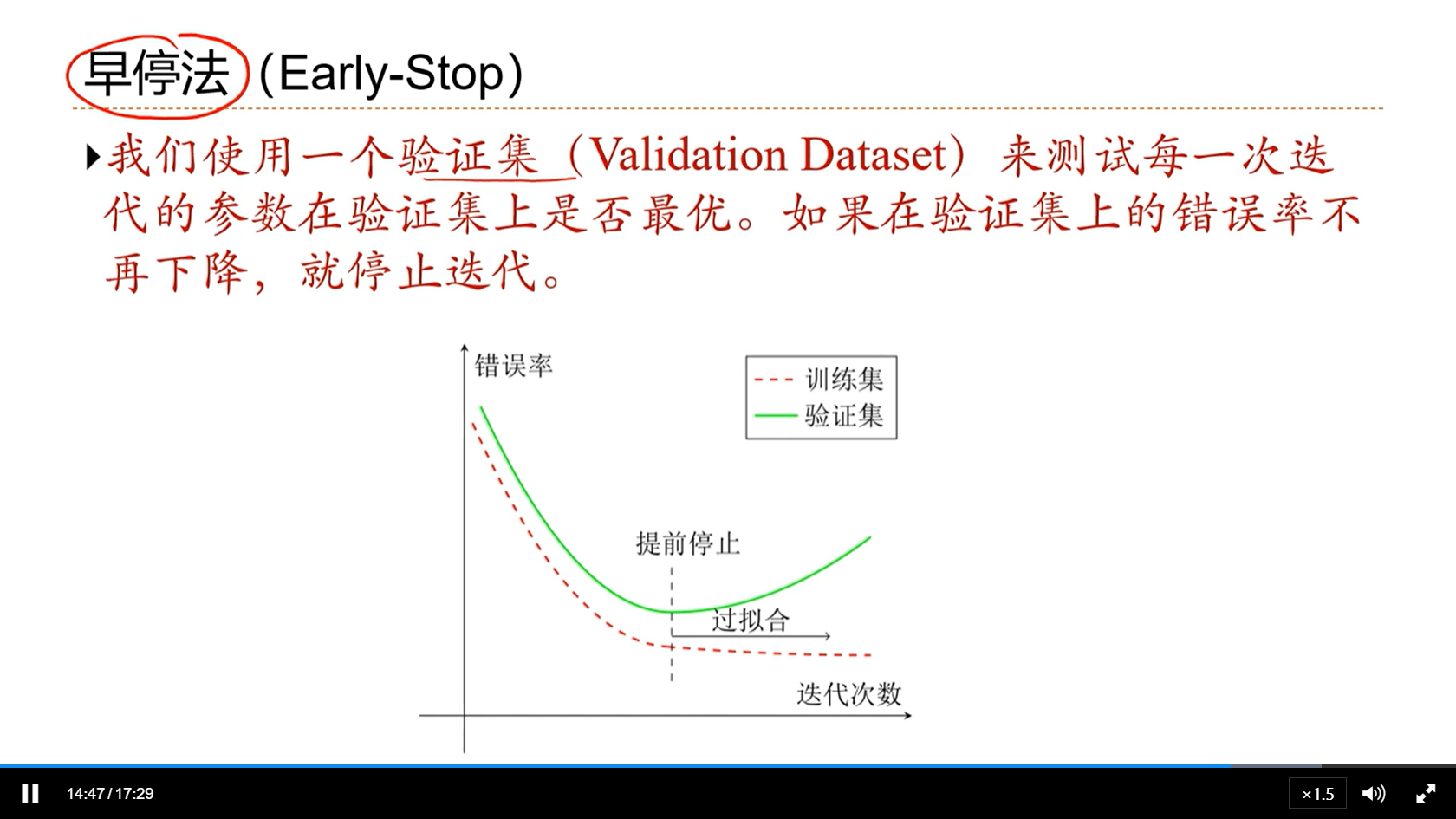
alec:
- 通常来讲,神经网络优先记住一般性的规范,然后再记住难的规则
- 因此可以早期停止
[√] 权重衰减(Weight Decay)

alec:
- 权重衰减和L_2范式的正则化,存在关联
- 权重衰减和动量法存在关联,动量法是δ梯度,群众衰减是梯度
[√] 7.10 - 两种正则化方法:L_1和L_2正则化
[√] L1和L2正则化

[√] 神经网络示例

可以看出,隐藏层的神经元数量越多, 模型越复杂,可能会过拟合
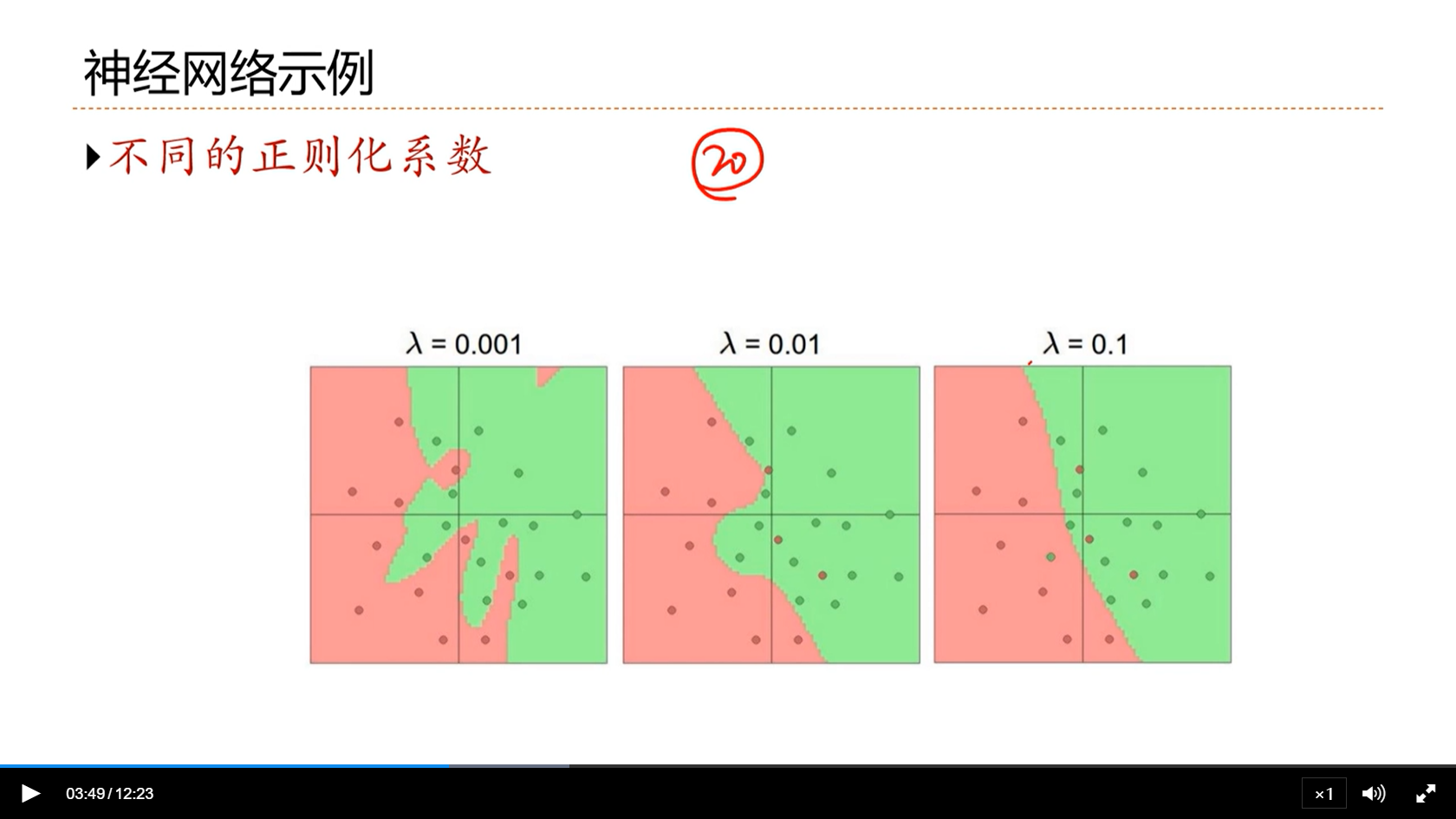
可以看出,正则化的系数越大,越能缓解过拟合的现象
[√] L2正则化与权重衰减
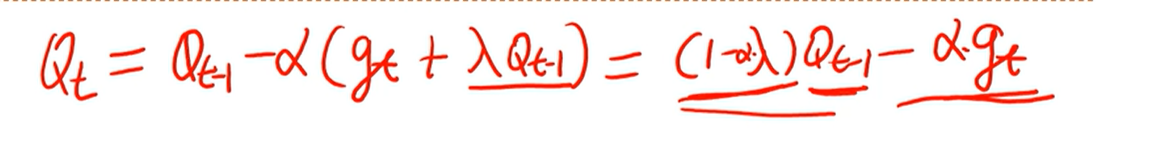
alec:
- 上式是带L2正则化项的参数更新公式。可以看出,正则化项相当于对上一次的参数做了一个αλ倍的衰减。
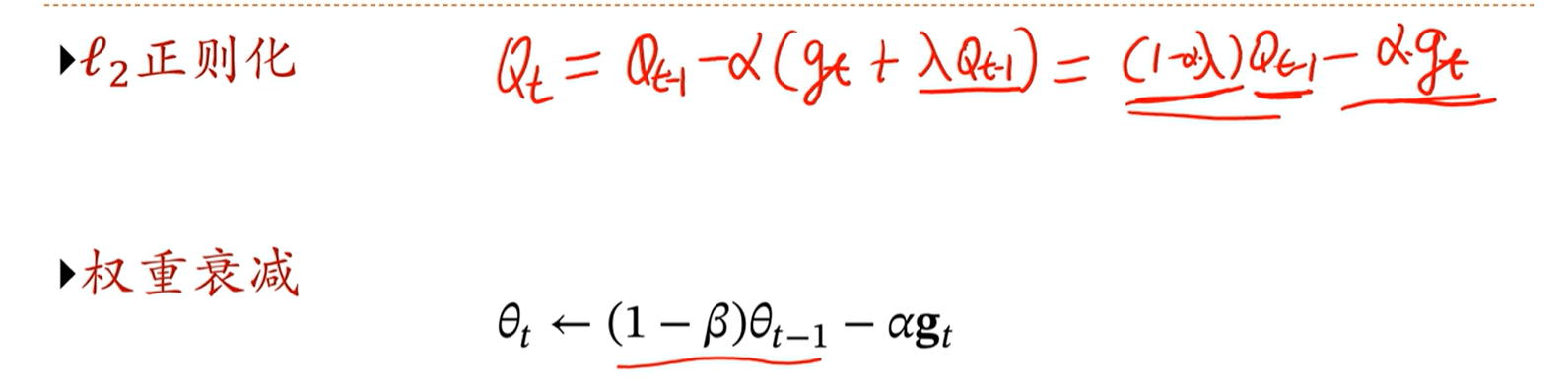
alec:
- 这种做法就和权重衰减一样了

[√] 7.11 - 暂退法(dropout)
[√] 暂退法
alec:
- 同一层的所有神经元,一起增大一起减小,这样可能鲁棒性不好,因此可以随机的暂退一些神经元
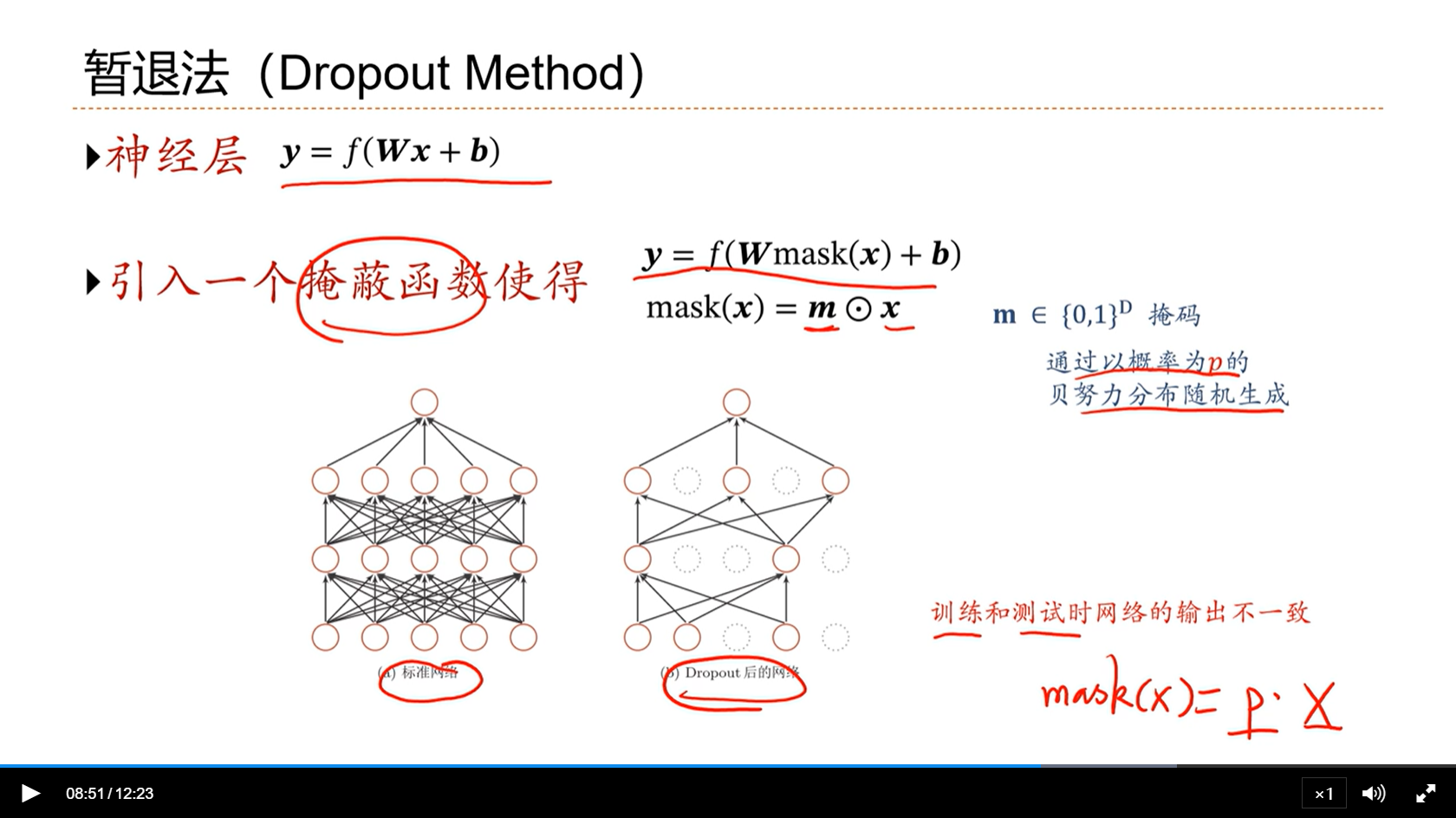
alec:
- 暂退法存在的问题:训练的时候暂退一些神经元,测试的时候用全部的神经元,导致训练的时候和测试的时候网络不一样。因此需要想办法解决这个问题。
- 方法是:暂退的时候,以概率P暂退。因此测试的时候,不是以概率p的暂退了,而是把每个神经元的活性值变为原来的P倍。
- 神经网络的每一层,所有的神经元,不是指的参数,而是指的通道特征图。网络的连接权重,体现在层与层之间的连接上。
[√] Dropout意义
alec:
- 暂退法,是一种正则化方法。能够提高网络的能力,就是提高所谓的泛化性。

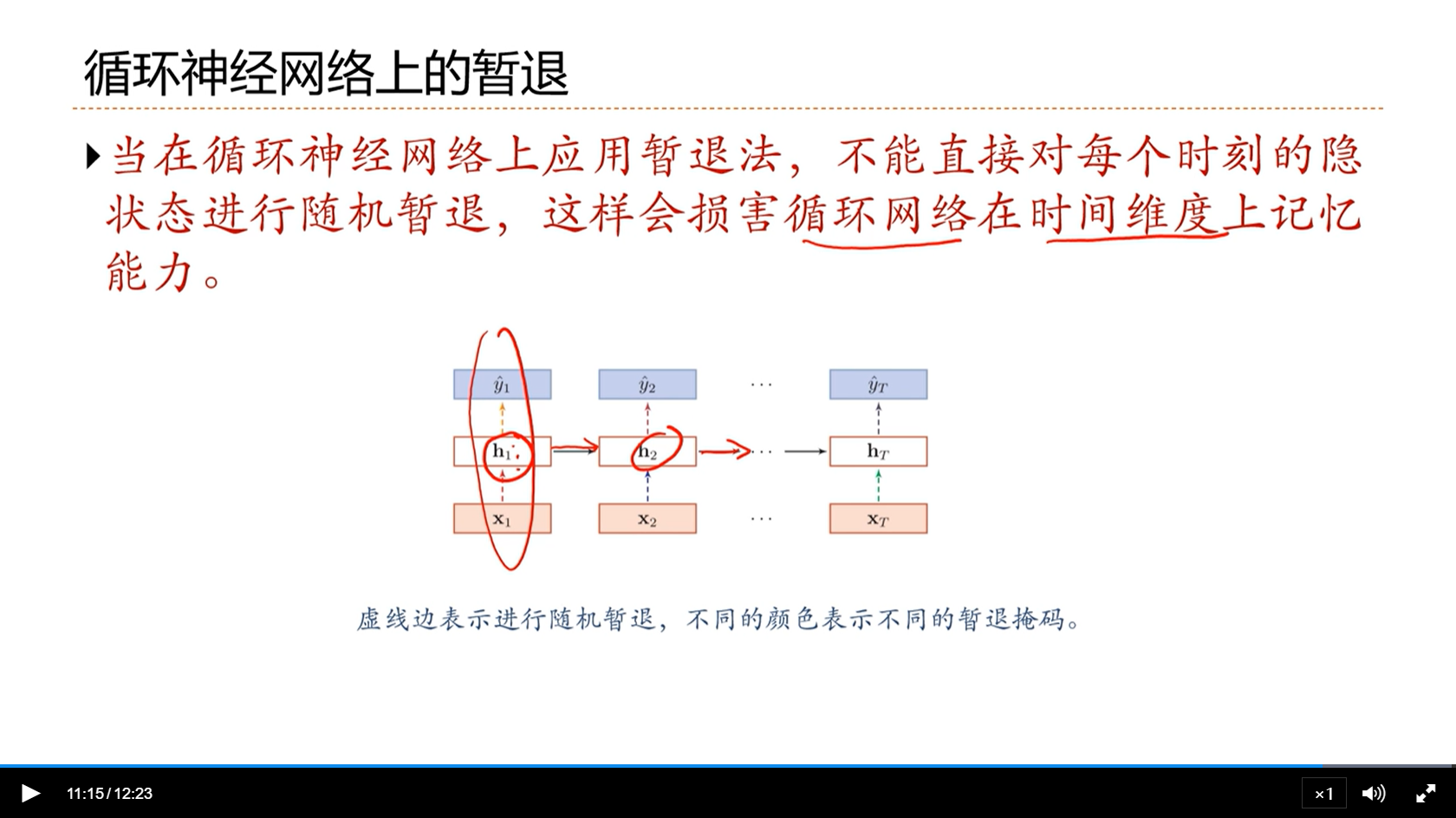
[√] 循环神经网络上的暂退
alec:
- 当在循环神经网络上应用暂退法,不能直接对每个时刻的隐状态进行随机暂退,这样会损害循环网络在时间维度上记忆能力。
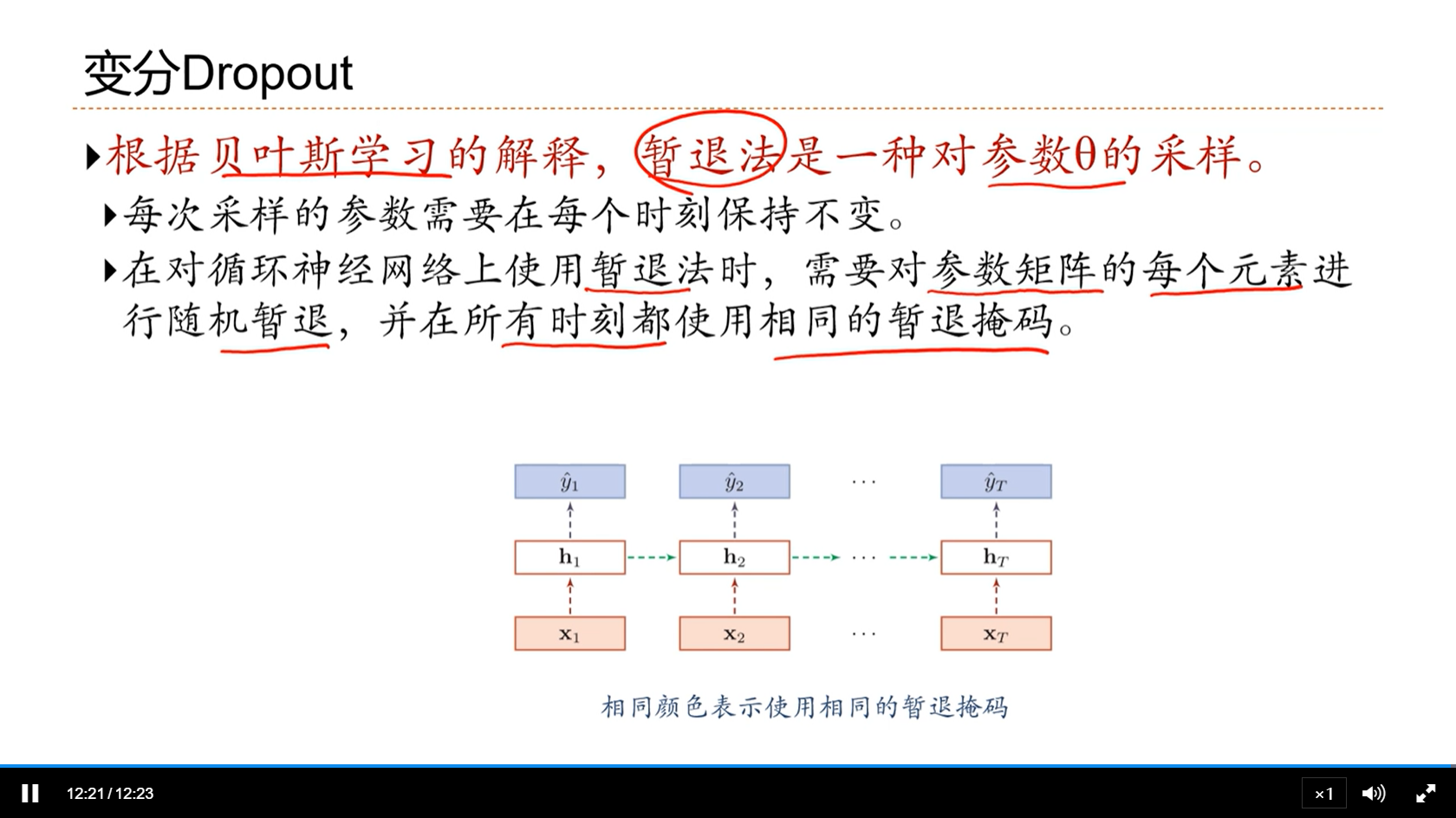
[√] 变分Dropout
[√] 7.12 - 数据增强和总结
[√] 数据增强(Data Augmentation)


alec:
- 文本数据增强,因为都要把单词转为向量,因此还有一些方法在隐式的向量空间做数据增强。
[√] 标签平滑(Label Smoothing)

alec:
- 标签的平滑,可以让网络的鲁棒性更高。

alec:
- 假设标签yi和yj二者的概率是比较近的。如何让这两个标签在标签向量上有关联性呢?
- 一种方法是知识蒸馏:我们可以在一个大模型上预训练这个数据集,数据集经过大模型之后,输出的Y’蕴含了某种语义相关性,然后将Y’再用到小模型上,从而可以指导小模型的训练
[√] 7.13 - 小结

7 - 网络优化与正则化
https://alec-97.github.io/posts/1207574521/