第4章 - 前馈神经网络 - 视频

本文最后更新于：3 个月前

[√] 4.1 - 神经元和前馈神经网络

[√] D => 神经元 - 净活性值

image-20221217150208903

image-20221217150410382

image-20221217150505118

image-20221217150555919

image-20221217150624226

image-20221217150718241

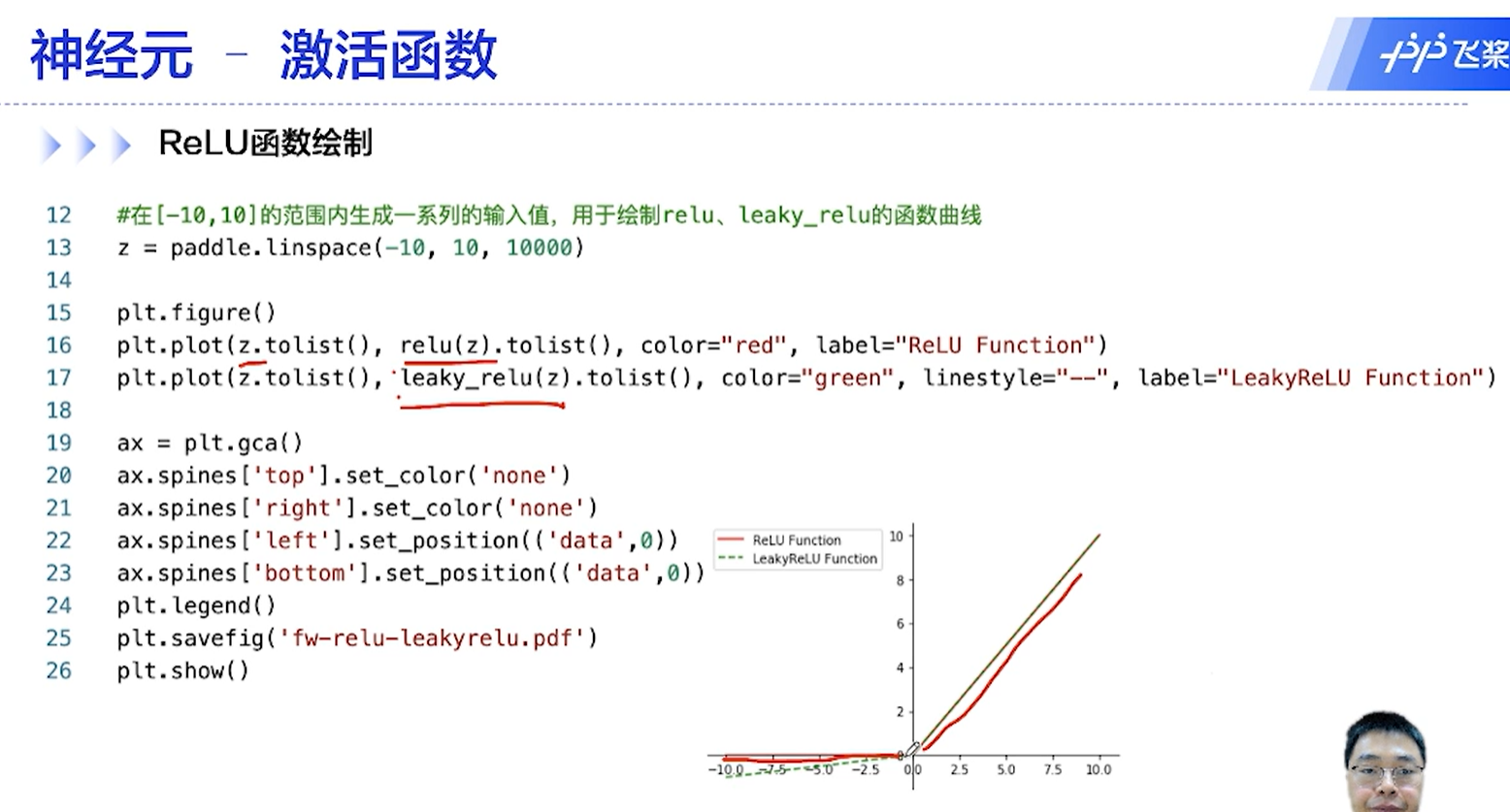
[√] F -> ReLU函数绘制

image-20221217151601341

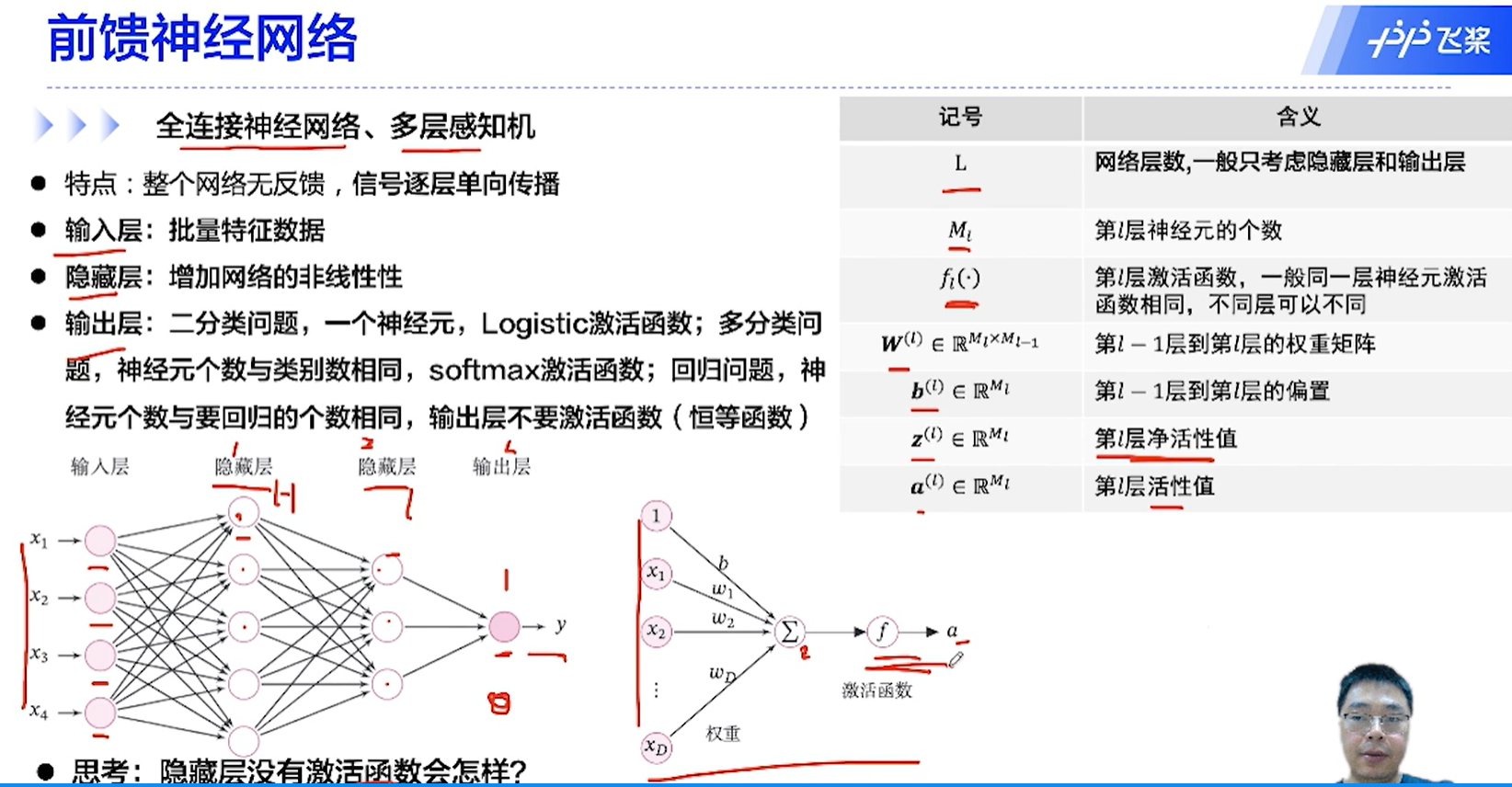
[√] D => 前馈神经网络

[√] F -> 全连接神经网络、多层感知机

image-20221217152359647

alec: 输出层什么时候使用激活函数？

分类问题，输出层一般有激活函数，因此要做成概率来表示分类的可能性

回归问题，一般输出层不要激活函数，因为回归问题是直接预测的输出值

思考：如果隐藏层没有激活函数会怎样？

没有激活函数，函数计算的数值可能会随着层数的加深变得非常大从而溢出

没有激活函数那么全都是线性的，无法解决非线性问题

[√] 4.2 - 基于前馈神经网络的二分类任务

[√] D => 机器学习实践5要素

image-20221217153051359

[√] D => 数据集构建

[√] F -> 二分类数据集

image-20221217153207228

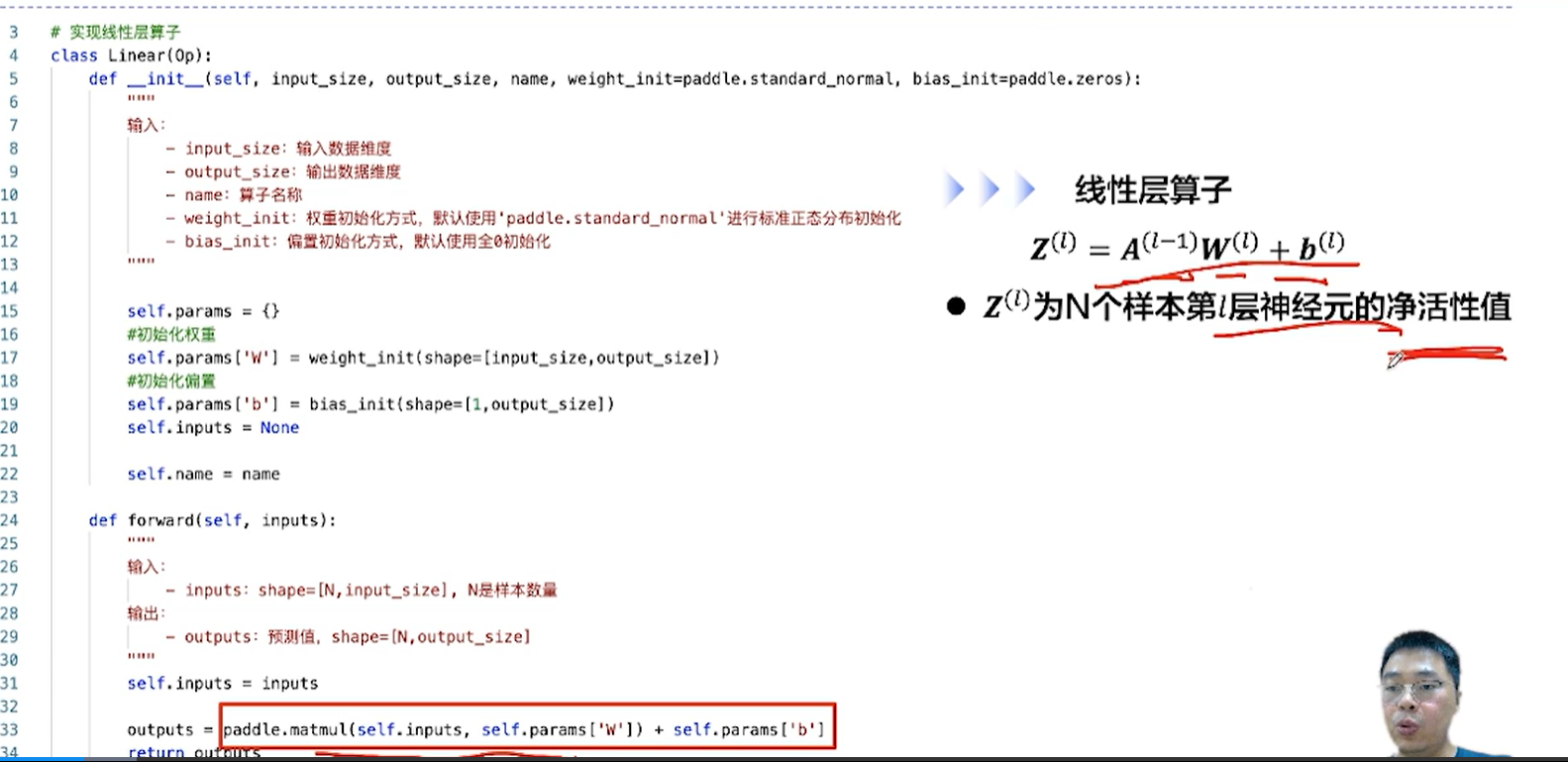
[√] F -> 线性层算子

image-20221217153529772

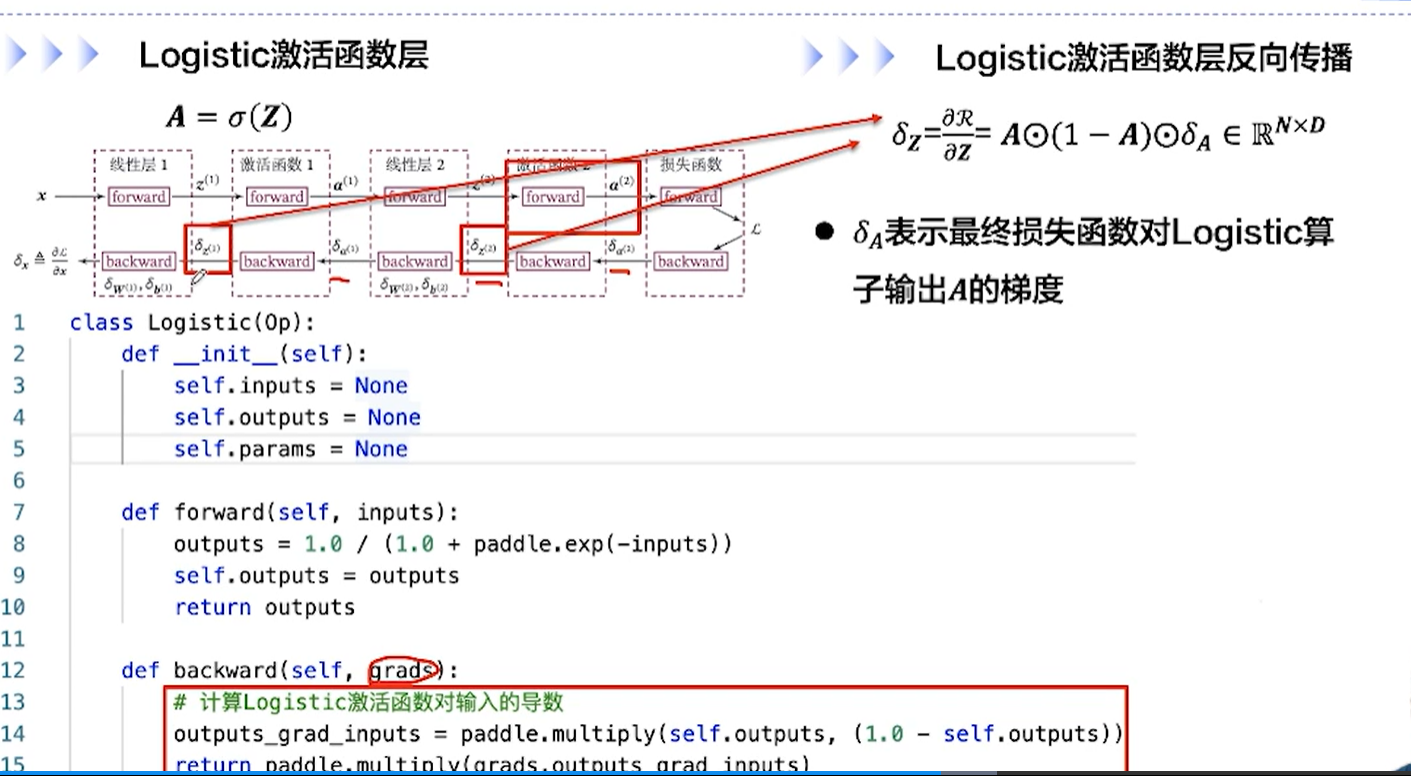
[√] F -> logistic激活函数算子

image-20221217153624034

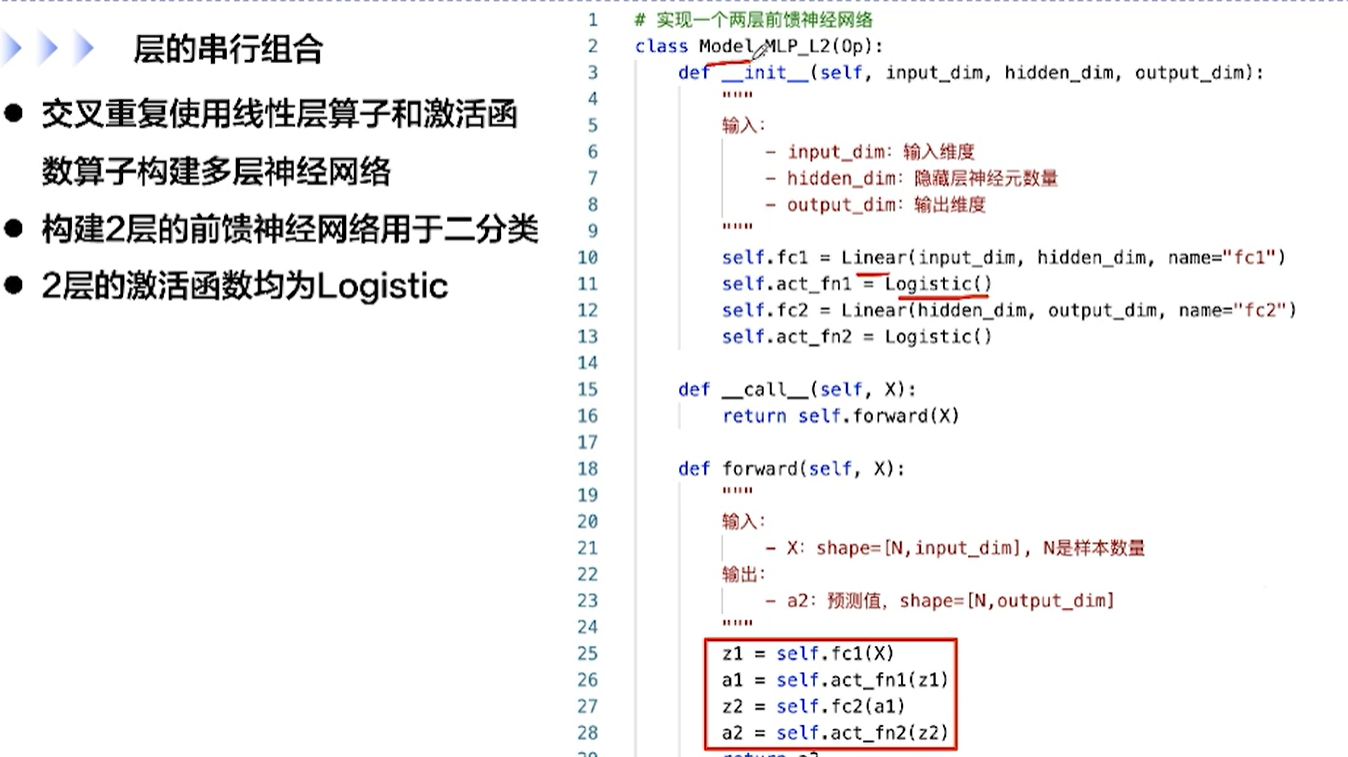
[√] F -> 层的串行组合

image-20221217153708226

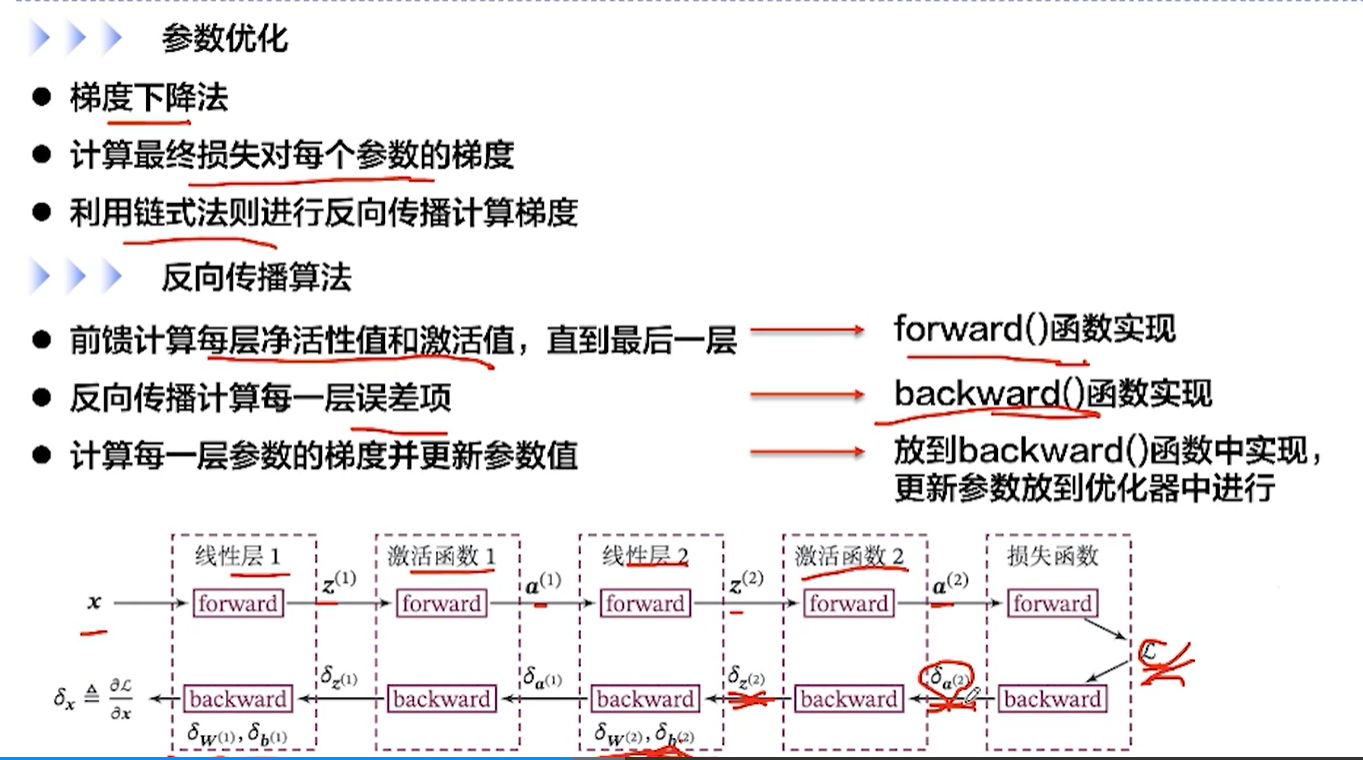
[√] D => 前馈神经网络的模型优化

[√] F -> 参数优化 + 反向传播算法

image-20221217154247581

image-20221217154445689

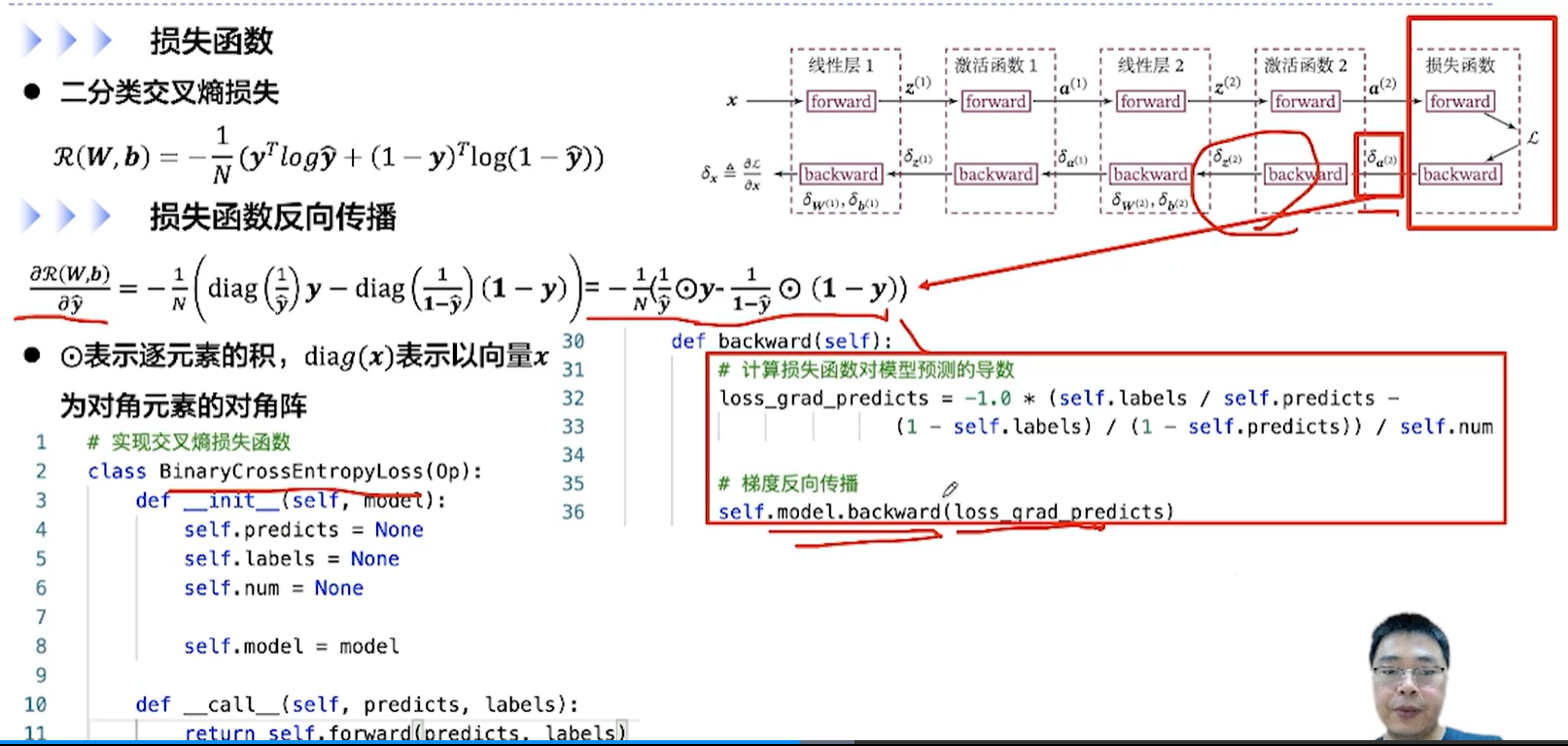
[√] F -> 损失函数 + 损失函数反向传播

image-20221217154635469

这是交叉熵损失函数的backward↑

[√] F -> 激活函数层的反向传播

image-20221217155133070

这是logistic激活函数的backward↑

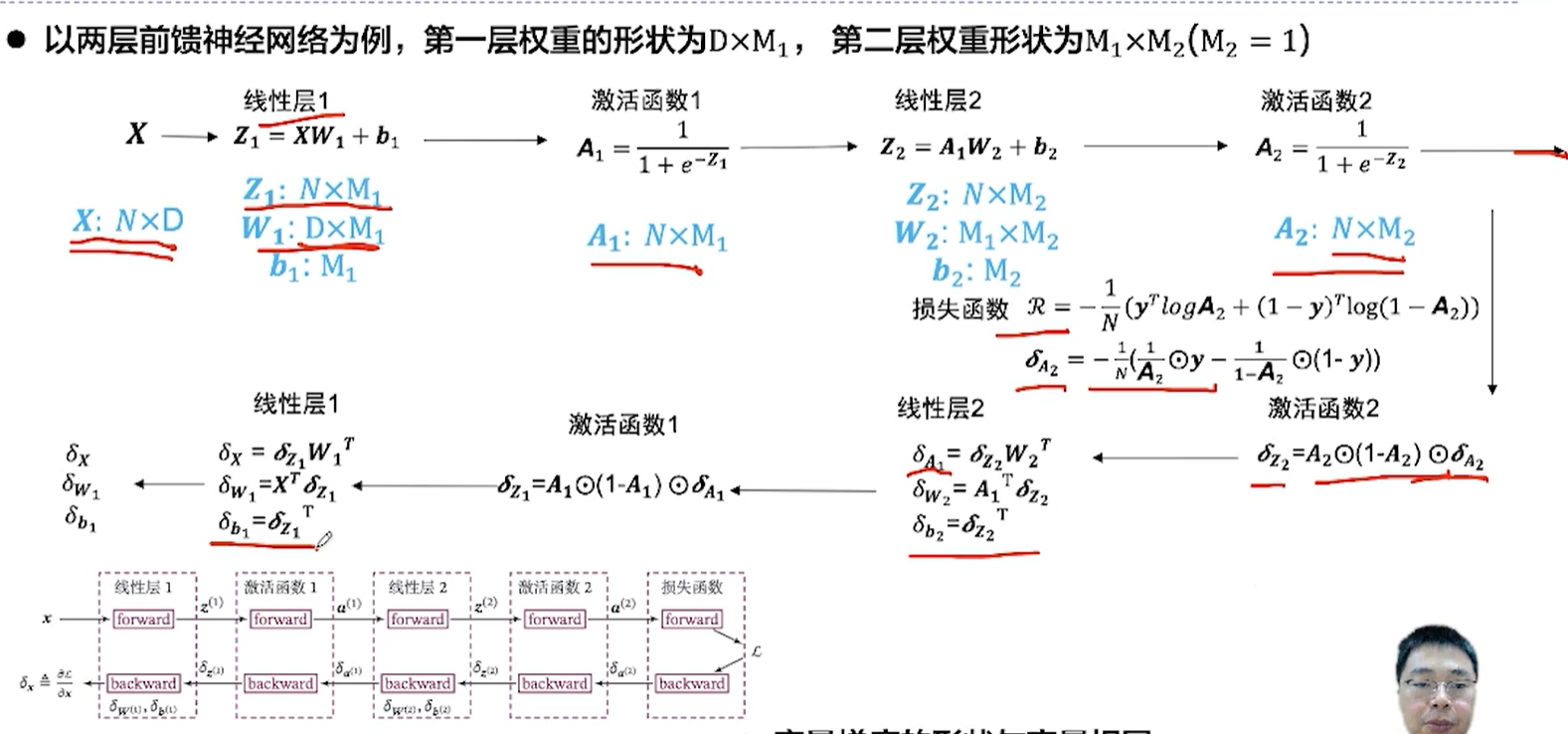
[√] F -> 线性层 & 线性层输入的梯度 & 线性层参数的梯度

alec：

每个层的算子都有一个backward，线性层、激活函数层、损失函数层

image-20221217155456677

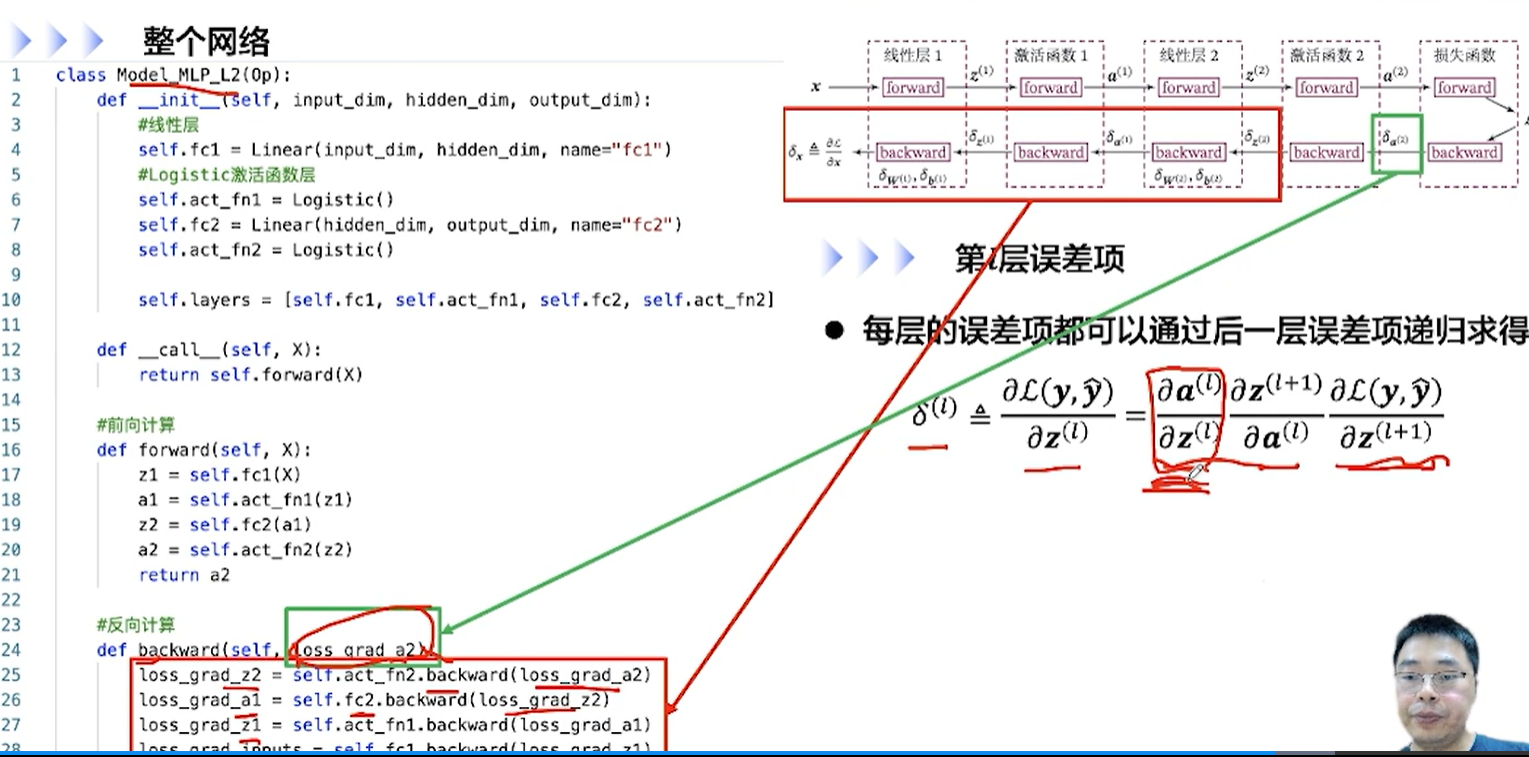
[√] F -> 整个网络的反向传播

image-20221217155933754

第一个backward的输入是损失函数对输出a2的梯度δ~a2~ ，然后逐层的往前反向传播。

其中fc指的是线性层。

alec：

先反向传播，把需要的这些梯度计算出来

然后后面调用优化方法的时候，会用到这些梯度里进行参数的更新

[√] F -> 优化器

image-20221217160129023

优化器的step方法用来进行参数的更新

遍历所有层，进行每一层的参数的更新

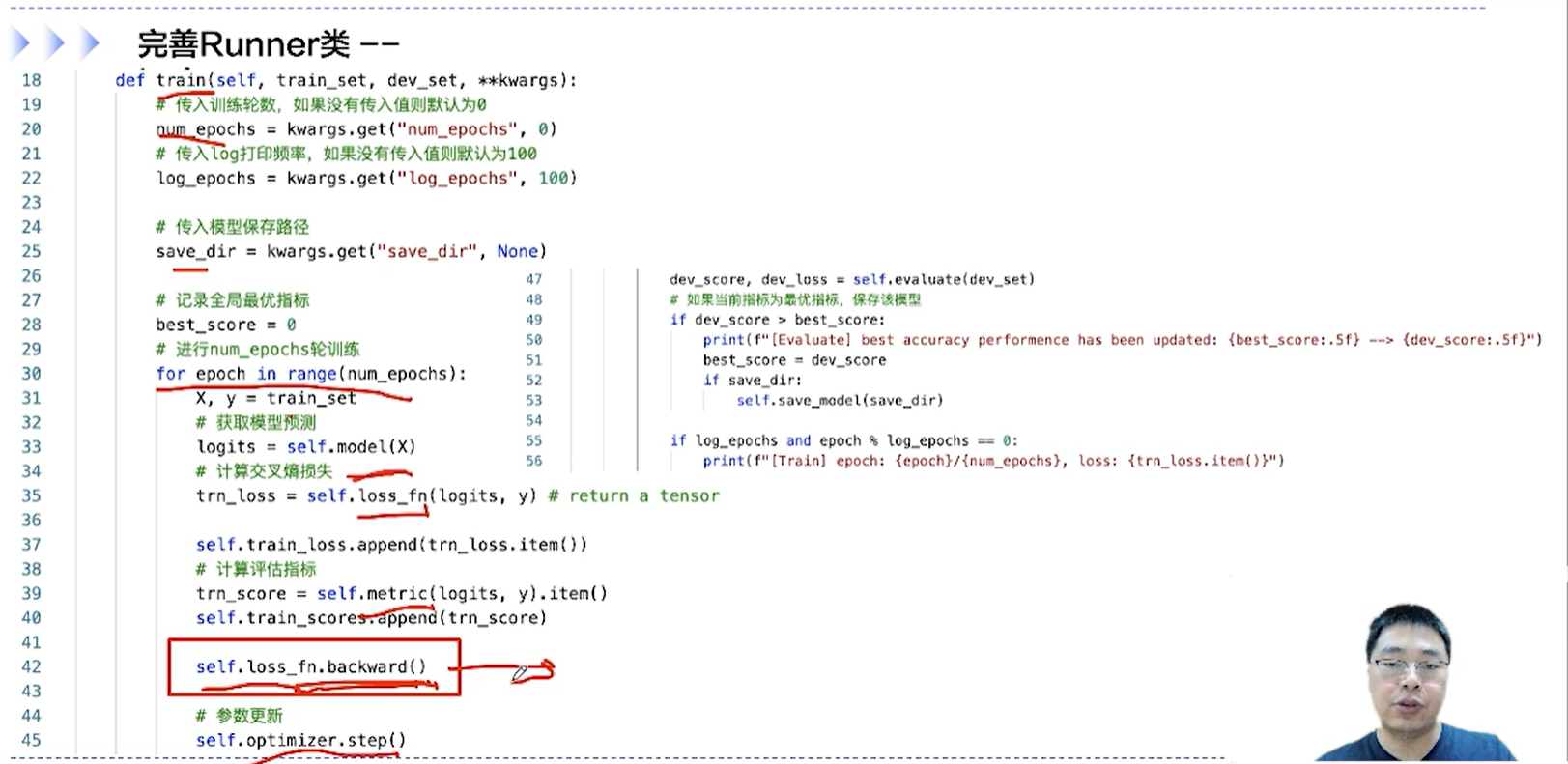
[√] D => Runner类

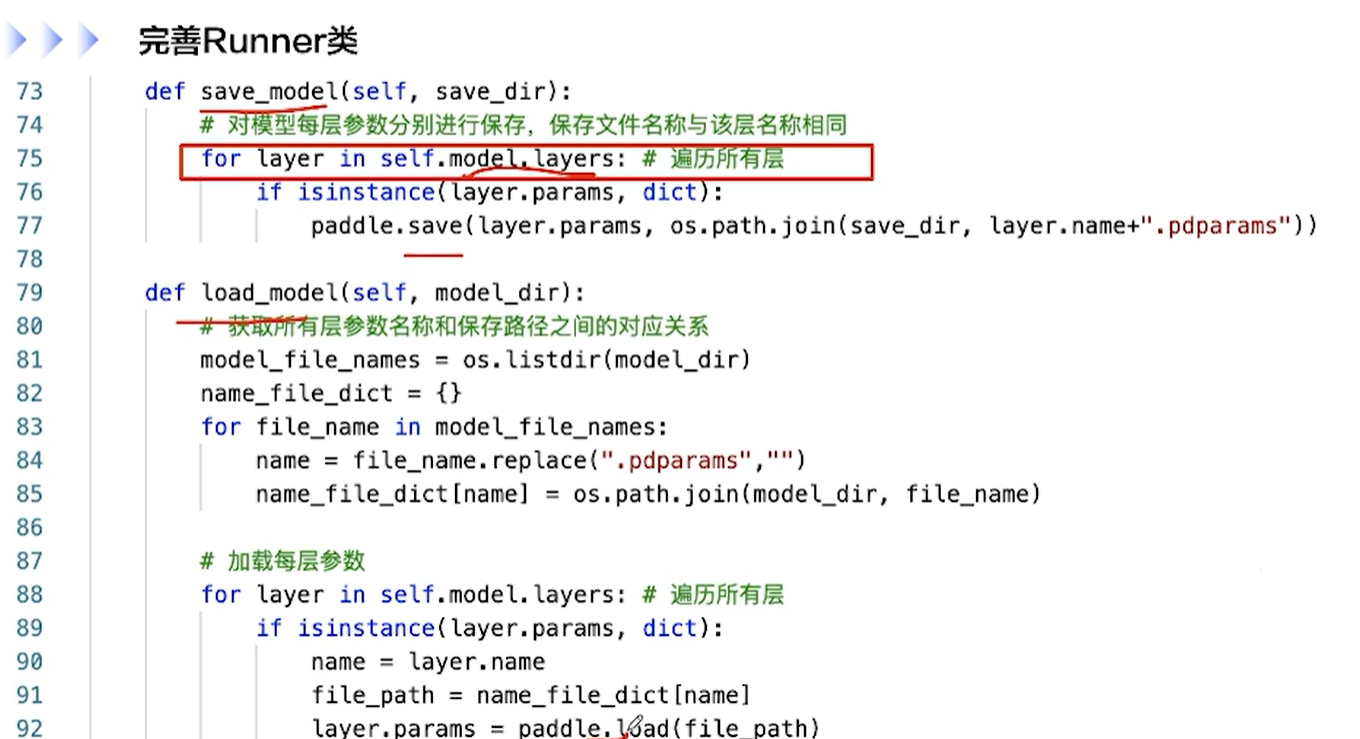
[√] F -> 完善Runner类

image-20221217160300062

image-20221217160325924

image-20221217160350834

image-20221217160527263

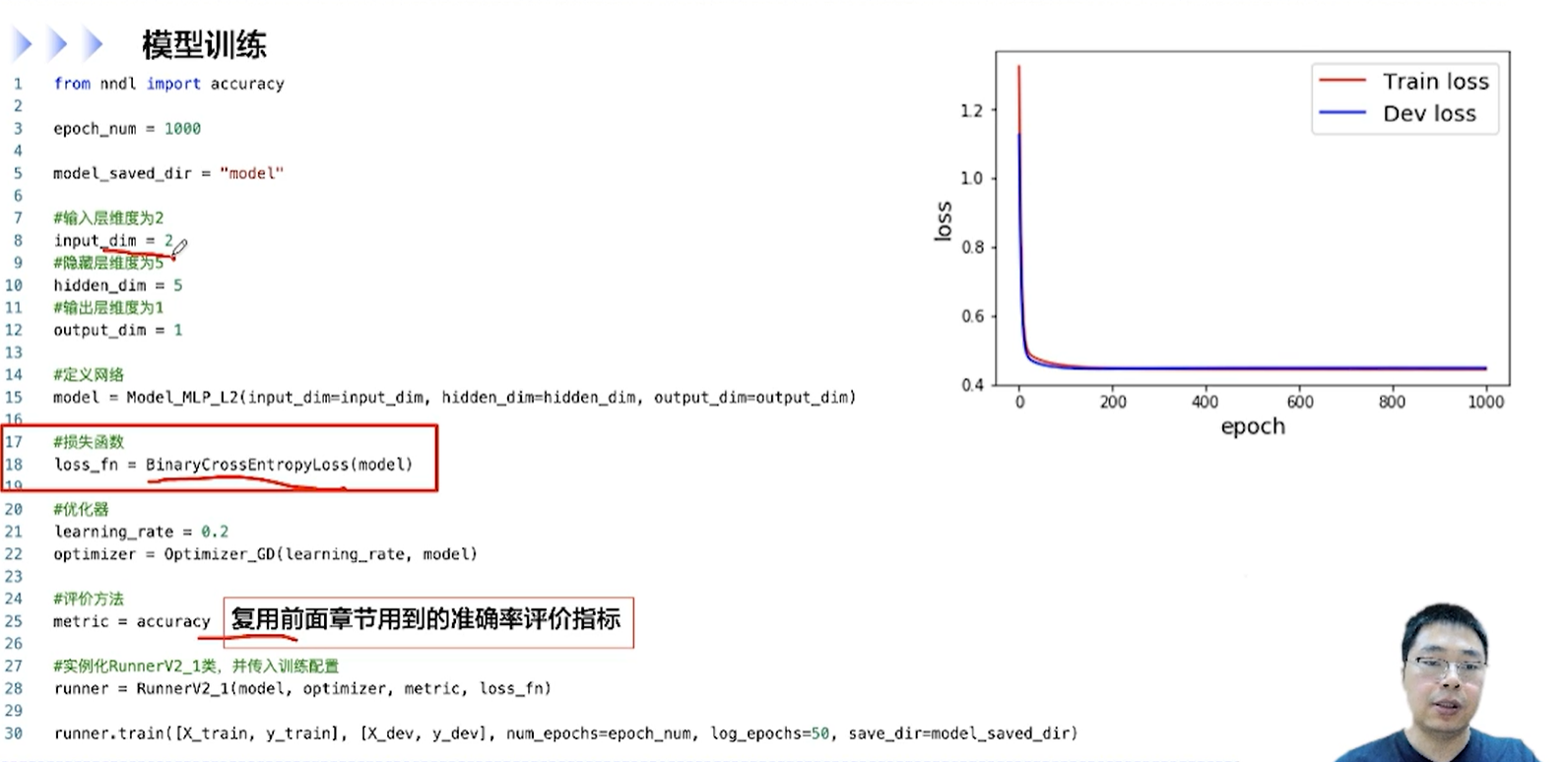
[√] F -> 模型训练

image-20221217160630996

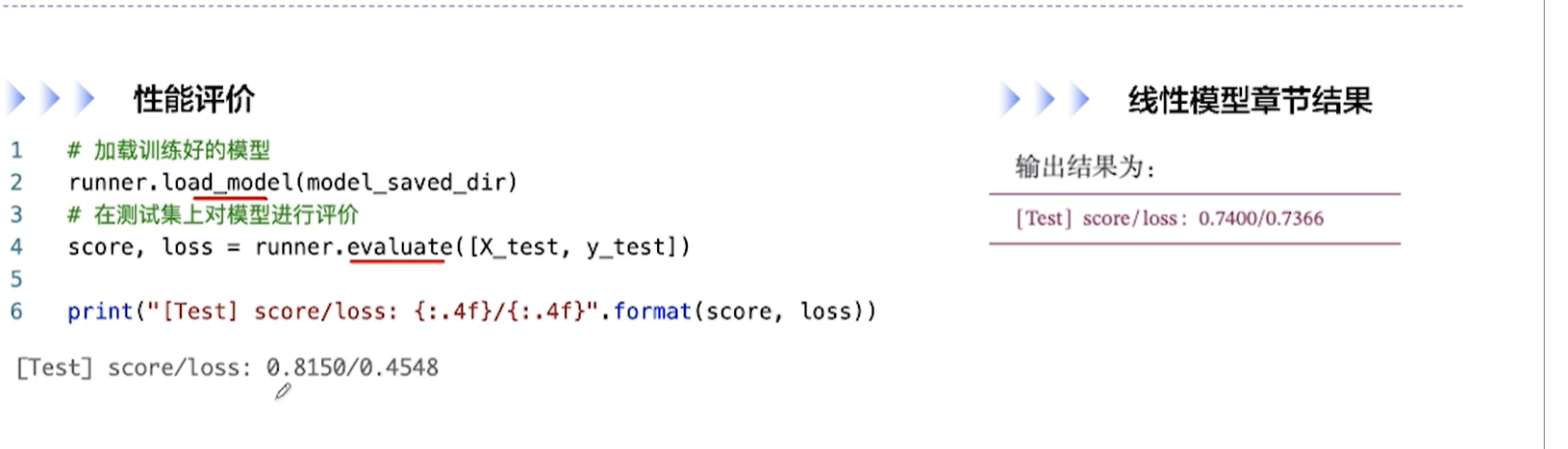
[√] F -> 性能评价

image-20221217160721891

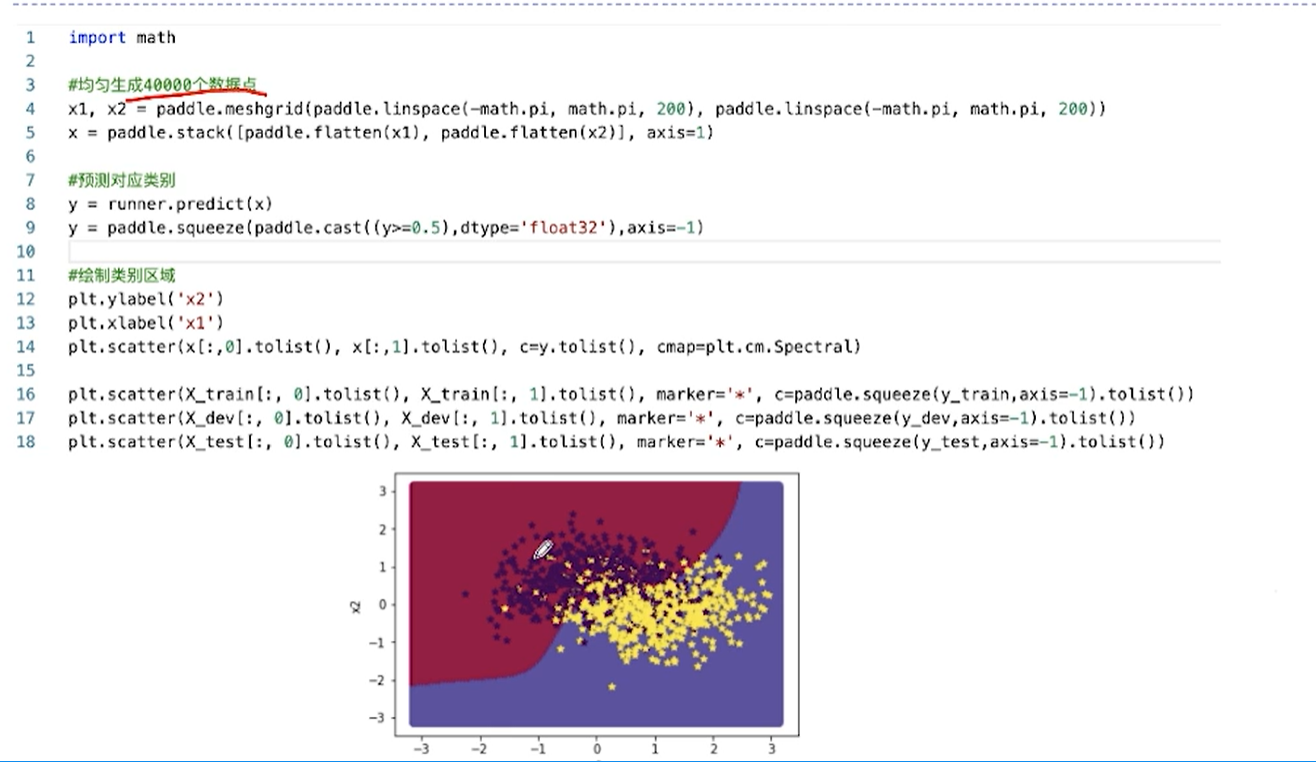
[√] D => 可视化

image-20221217160800466

可以看出，模型学习出的分界线是一个非线性的分界线。模型的分类效果更好。

[√] 4.3 - 自动梯度计算和预定义算子

[√] D => 重新实现前馈神经网络

[√] F -> 自动梯度计算 & nn.Layer & nn.Linear & nn

alec - nn.Layer和nn.Linear的区别：

  • Layer指的是一个模型
  • Linear指的是模型中的一层，Layer和Linear是包含与被包含关系

image-20221217163305414

[√] F -> 代码实现

image-20221217163655327

[√] D => 完善Runner类

[√] F -> RunnerV2_2

image-20221217163859825

[√] F -> 版本对比

image-20221217163940010

image-20221217164053403

自动进行梯度的计算和参数的更新

注意，参数优化更新之后需要清空梯度，顺序是：

  • backward 反向传播计算需要的梯度
  • step 利用计算的梯度进行参数的更新
  • clear 清空梯度

image-20221217164124581

模型的评估和预测阶段，关闭梯度计算和存储

[√] F -> 模型的训练

image-20221217164233292

[√] D => 性能评价

image-20221217164302567

[√] 4.4 - 优化问题

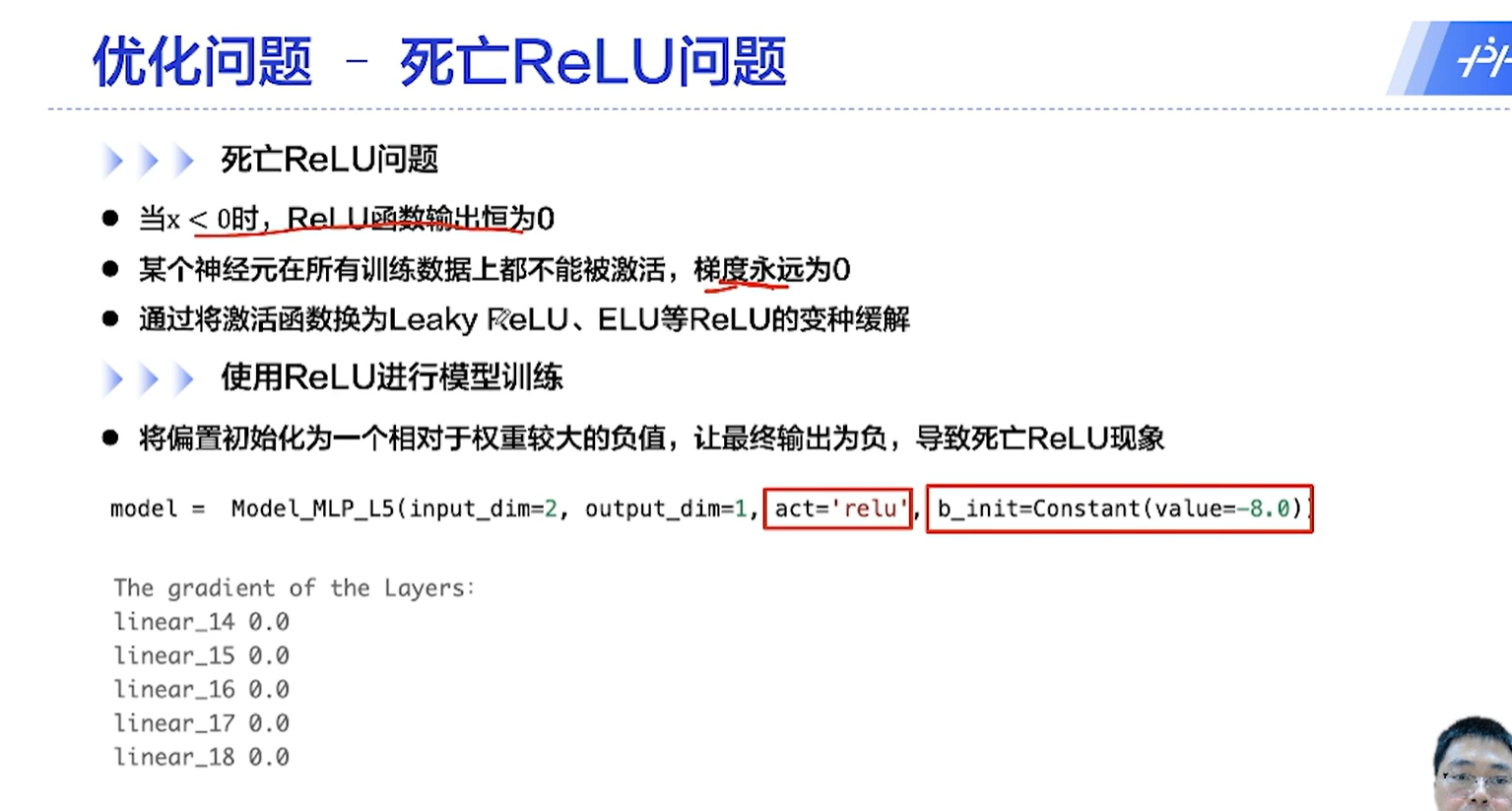
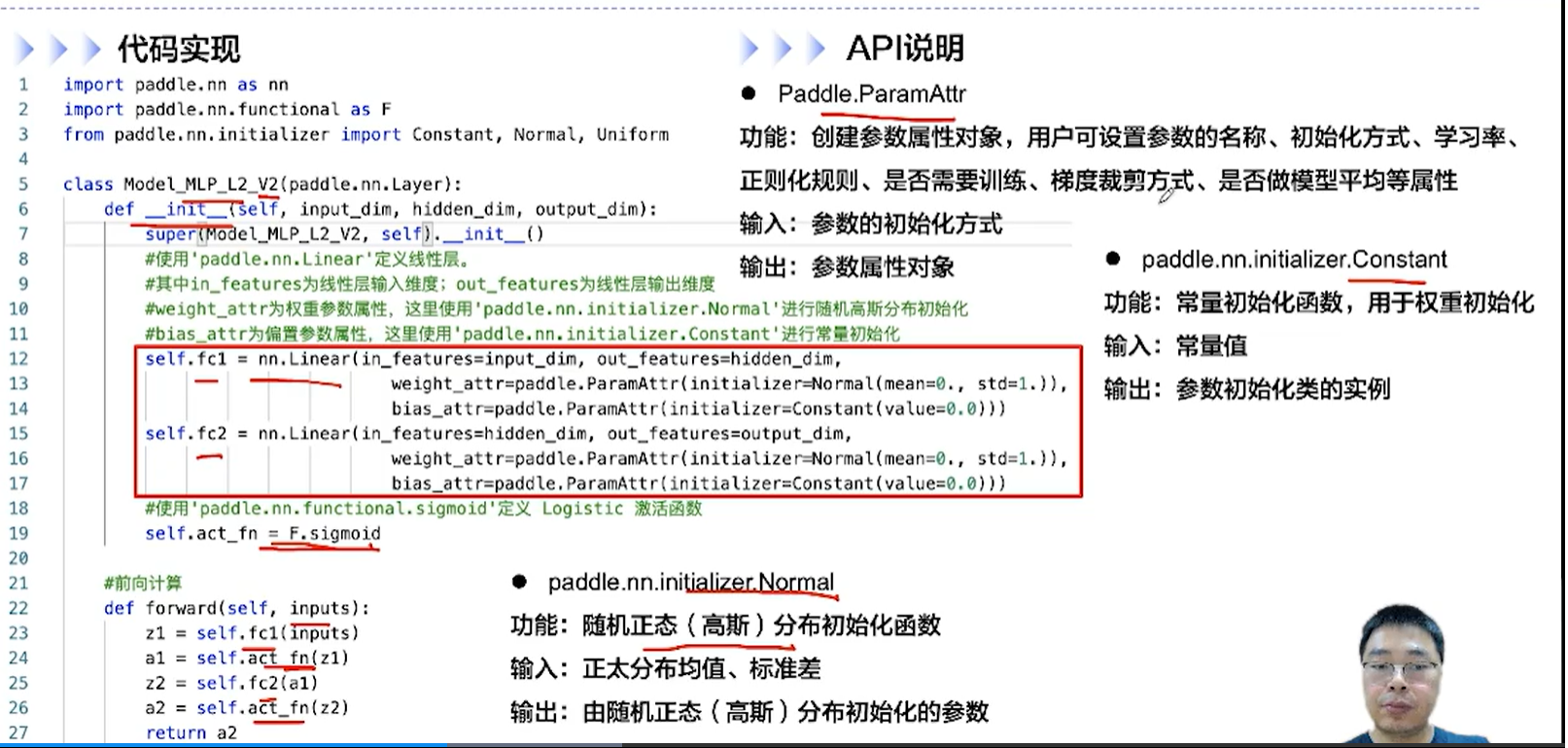
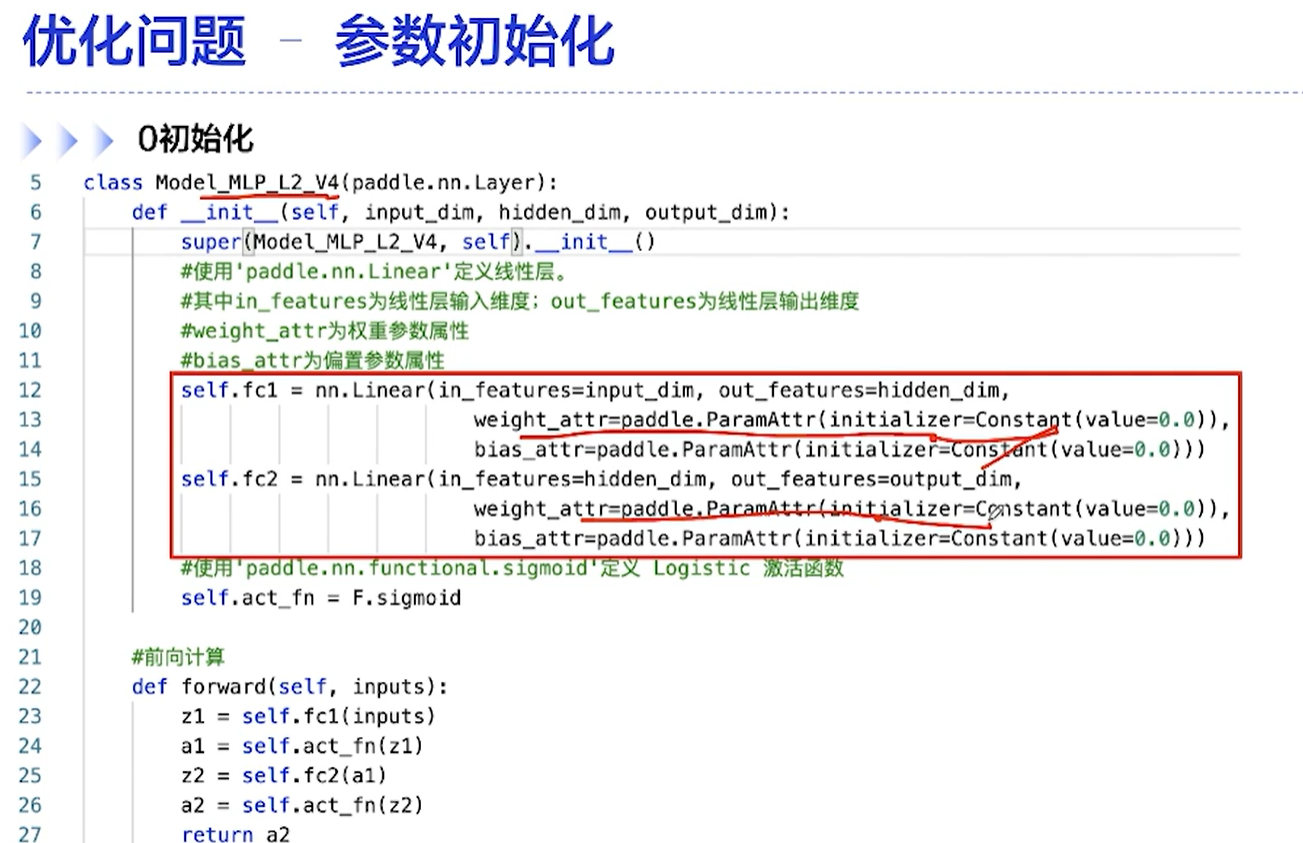
[√] D => 优化问题1 - 参数初始化

[√] F -> 0初始化

image-20221217165833209

0初始化的对称权重现象：所有隐藏层的激活值相同

image-20221217170022786

参数的初始化一般是使用非零的初始化，一般是使用高斯分布和均匀分布来初始化

image-20221217170125398

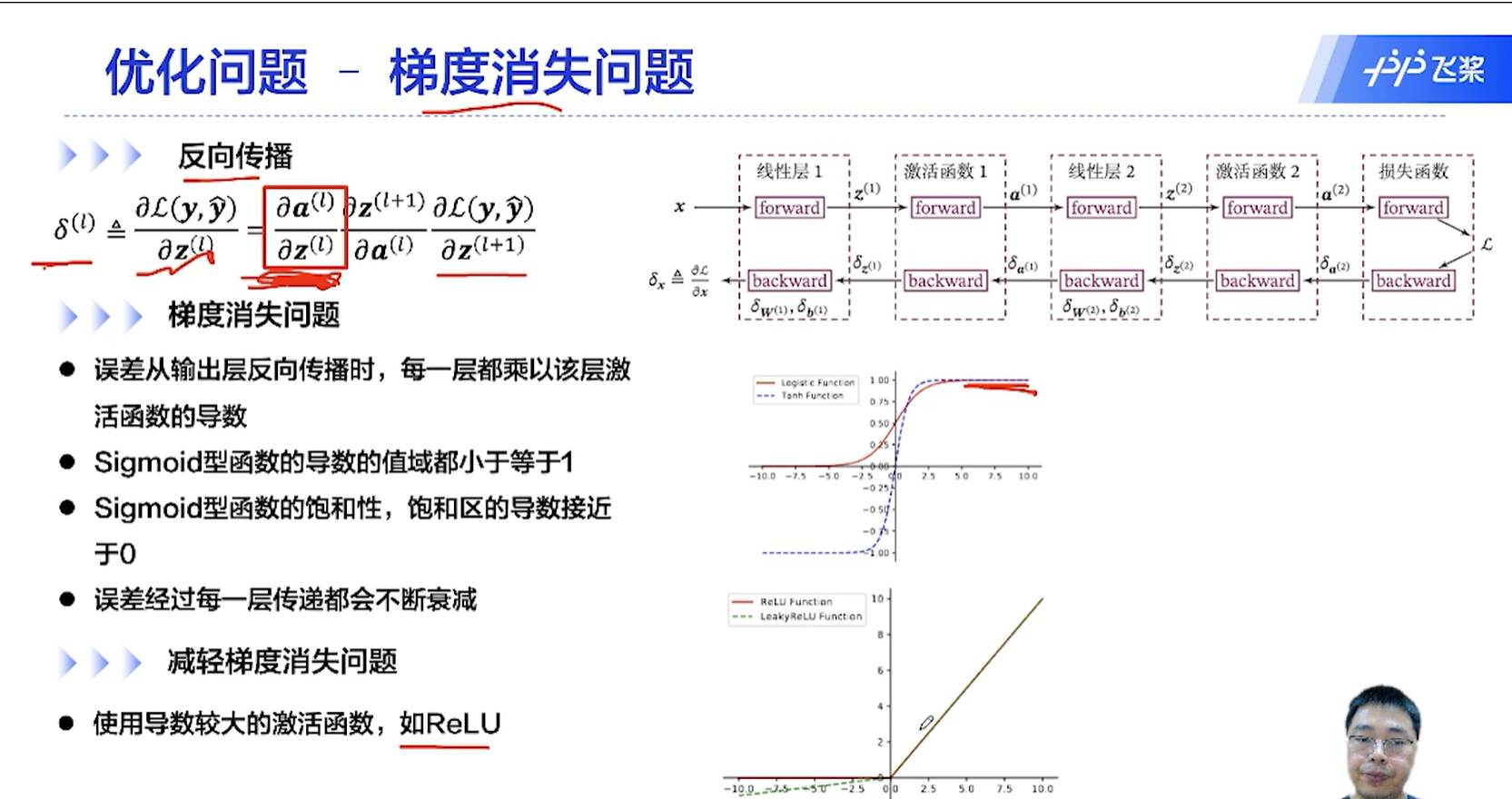
[√] D => 优化问题2 - 梯度消失问题

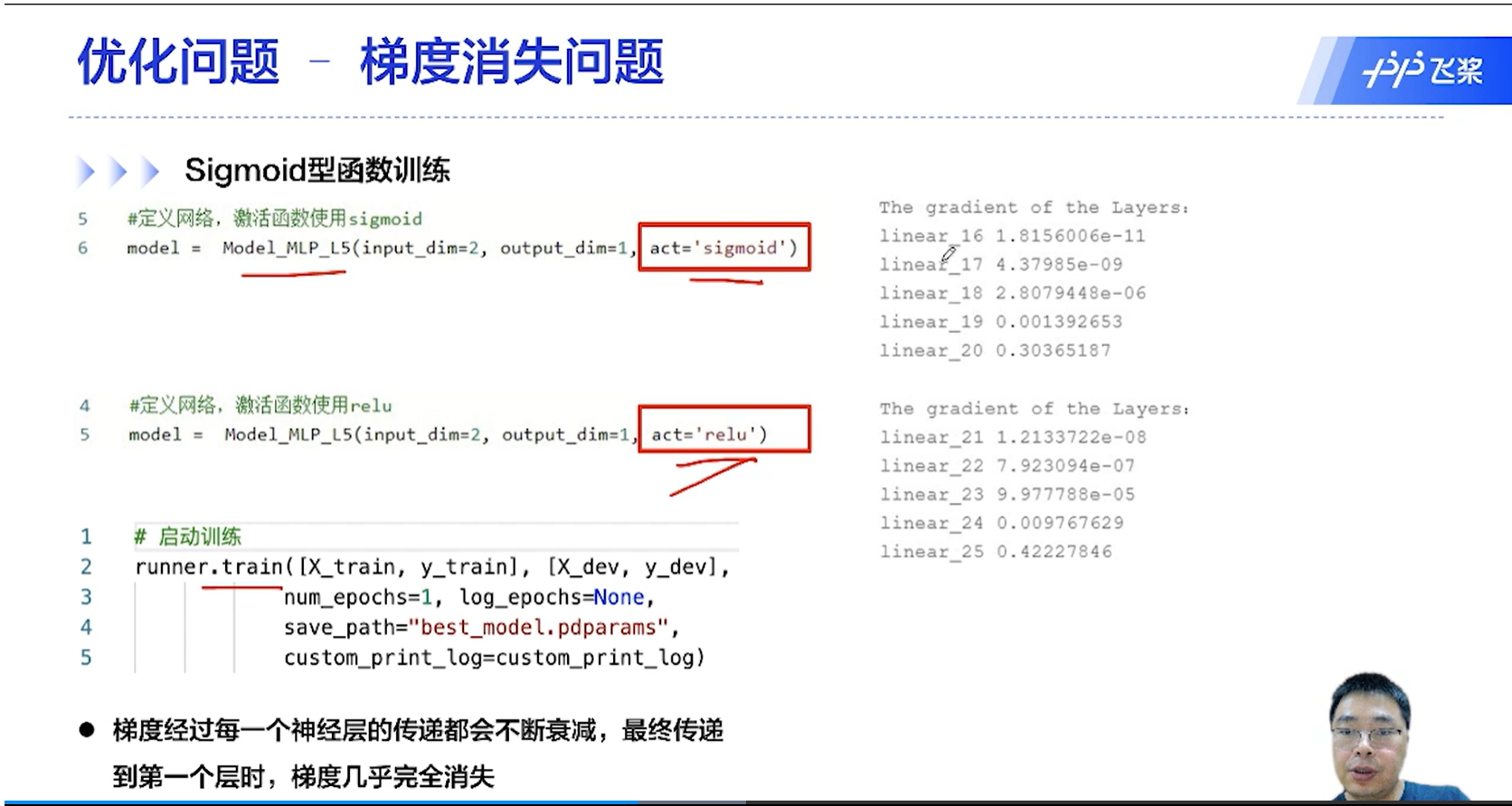
[√] F -> 反向传播 && 梯度消失问题 && 减轻梯度消失问题

image-20221217170358022

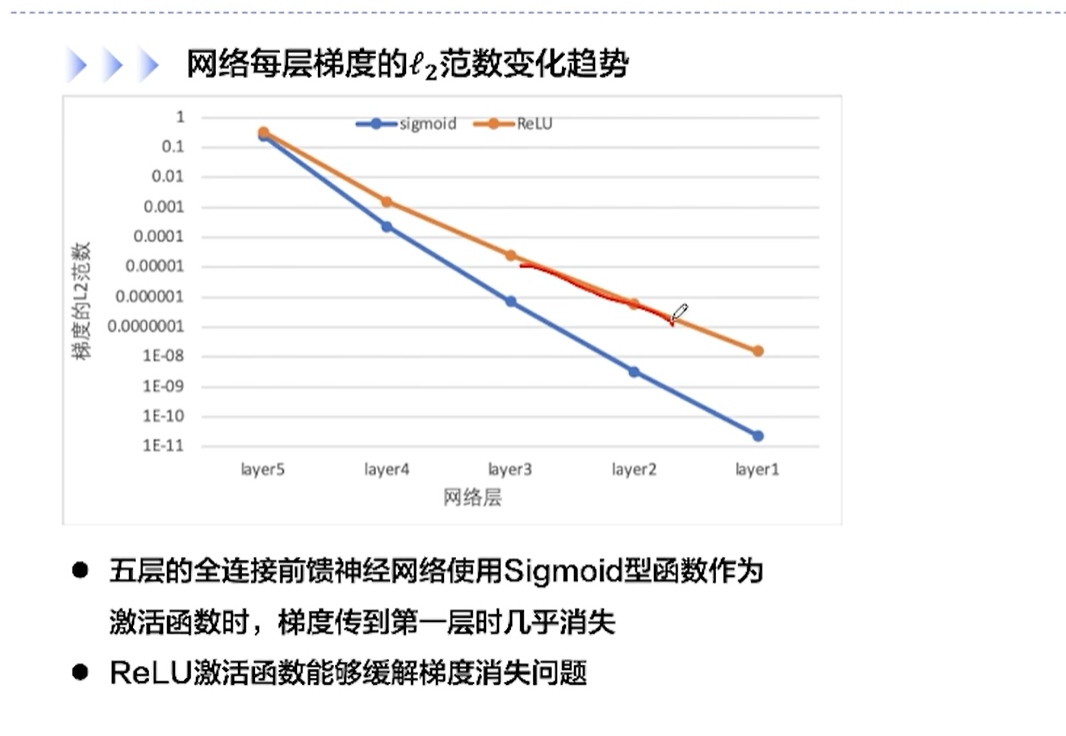
使用梯度比较稳定的激活函数缓解梯度消失问题

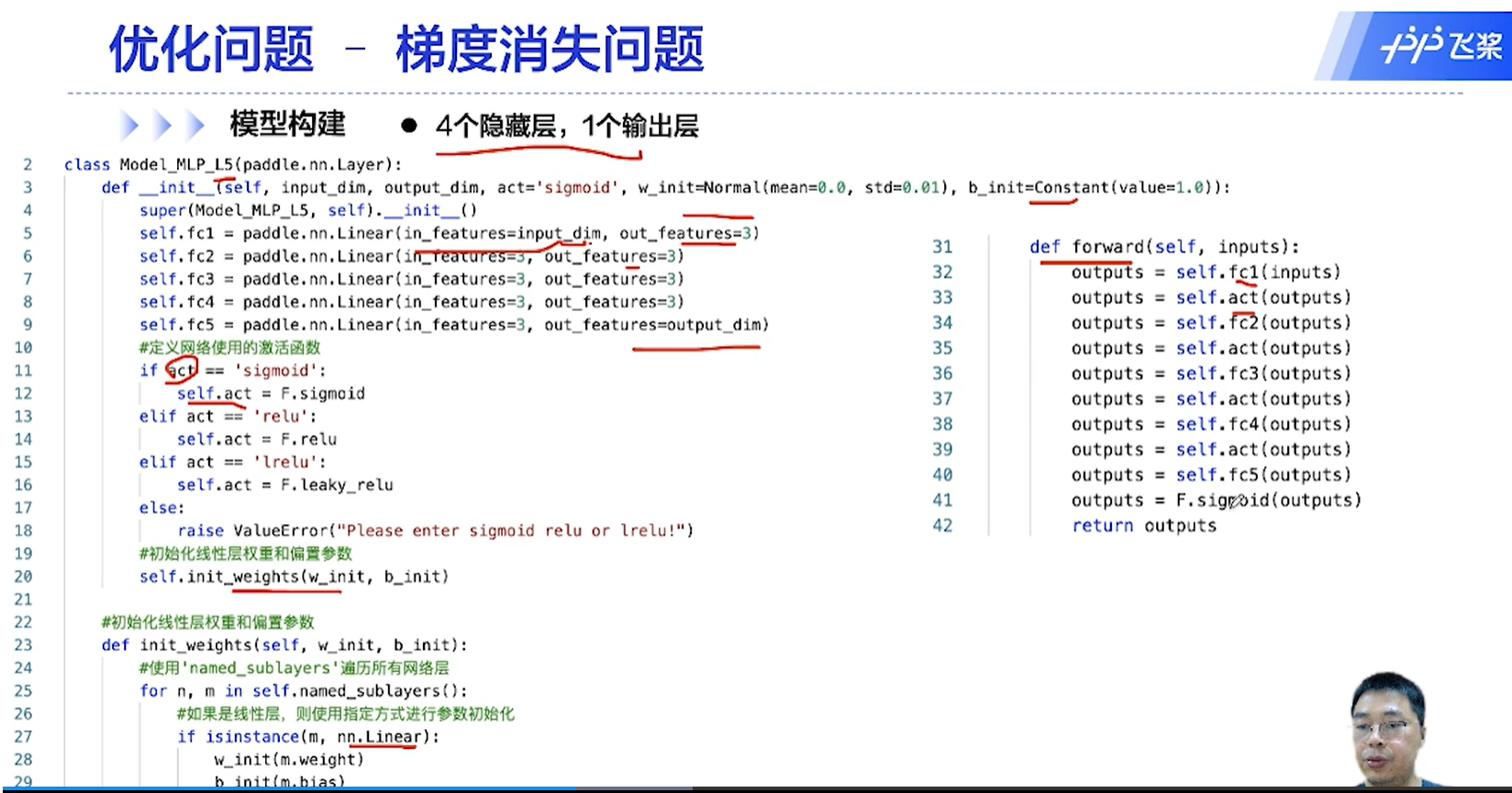
[√] F -> 模型构建

image-20221217170528466

image-20221217170612514

从后往前，梯度逐渐衰减，最前面的几层梯度就很小了。

[√] F -> 网络每层的梯度变化趋势

image-20221217170723956

[√] D => 优化问题3 - 死亡ReLU

image-20221217170841827

image-20221217170938635

[√] 4.5 - 前馈神经网络总结

image-20221217171436228

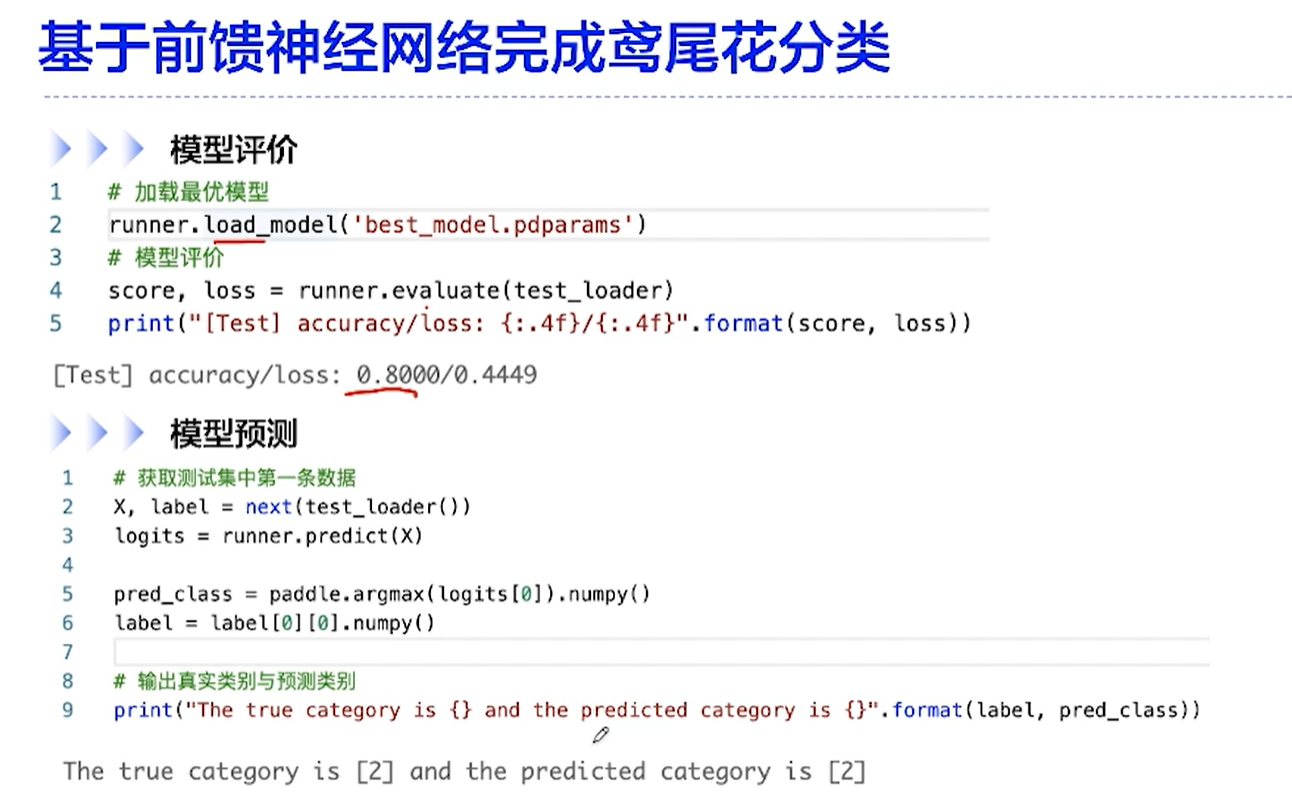
[√] 4.6 - 基于前馈神经网络的鸢尾花分类任务

[√] D => 机器学习实践5要素

image-20221217171755802

[√] D => 小批量梯度下降法

[√] F -> BGD批量梯度下降法 && mini BGD 小批量梯度下降法 && 参数更新

image-20221217172014449

[√] D => 数据处理

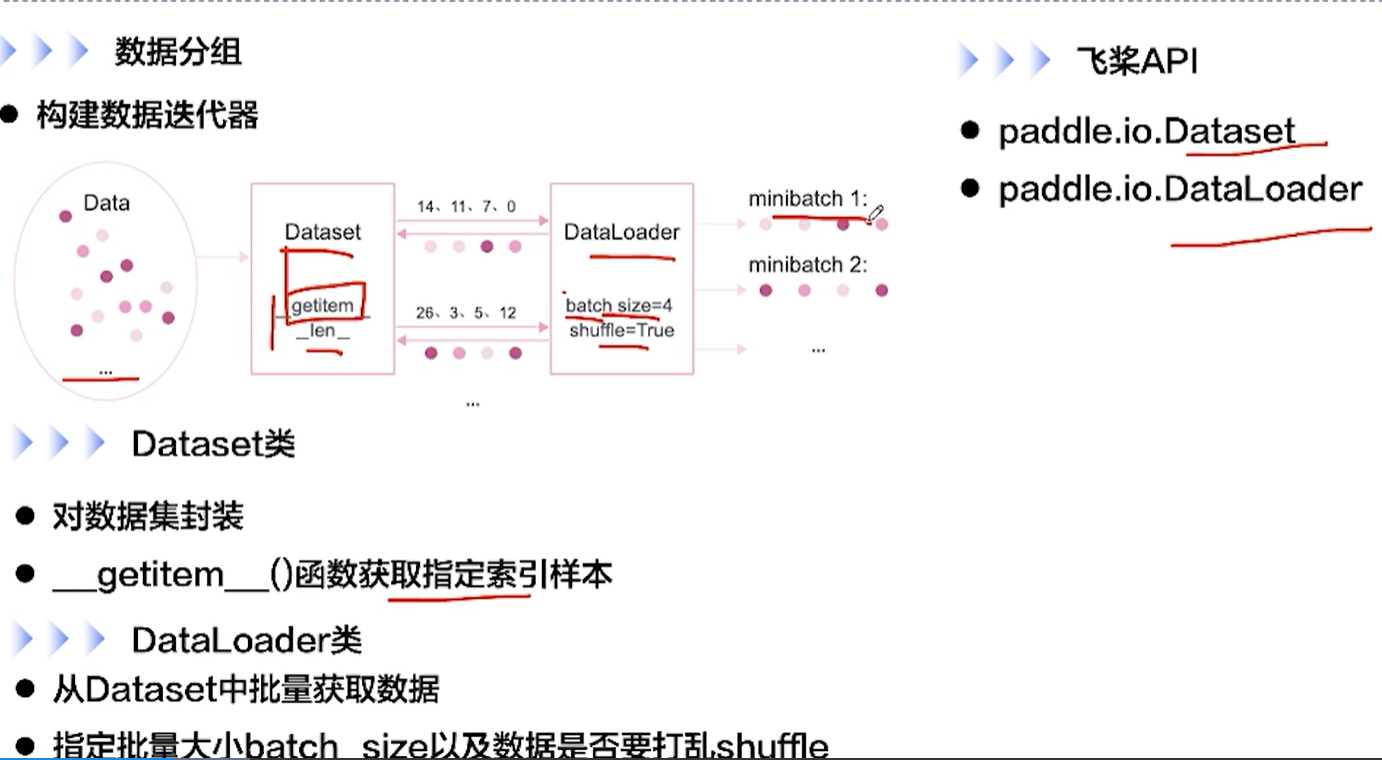
[√] F -> 数据分组 && Dataset类 && DataLoader类

image-20221217172823148

[√] F -> 构建IrisDataset

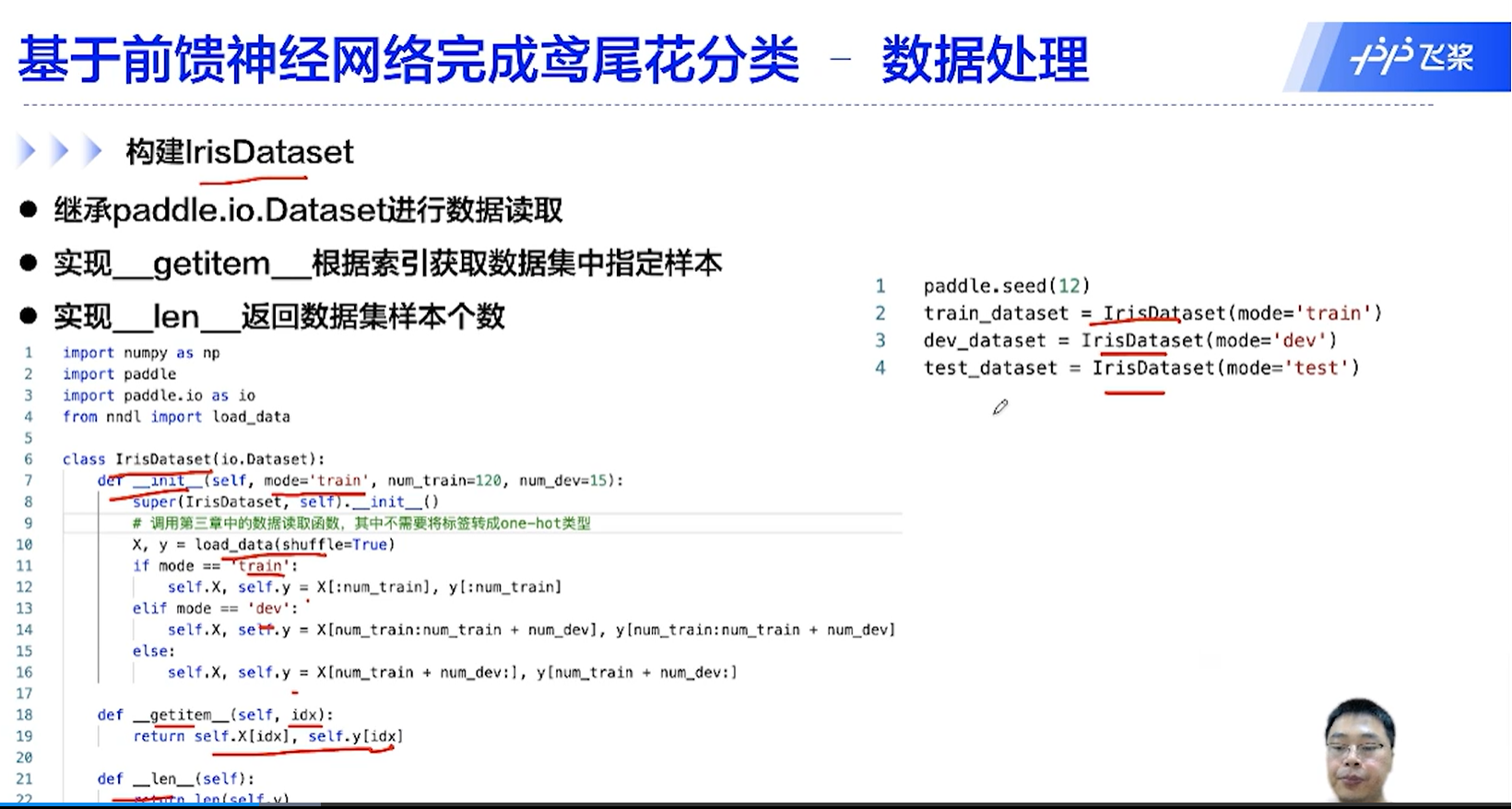
image-20221217173120736

[√] F -> 用DataLoader进行封装

image-20221217173925371

[√] D => 模型构建

[√] F -> 前馈神经网络 && 注意

image-20221217180742986

飞桨的损失函数中集成了softmax激活函数，因此前向传播这里最后没有加激活函数

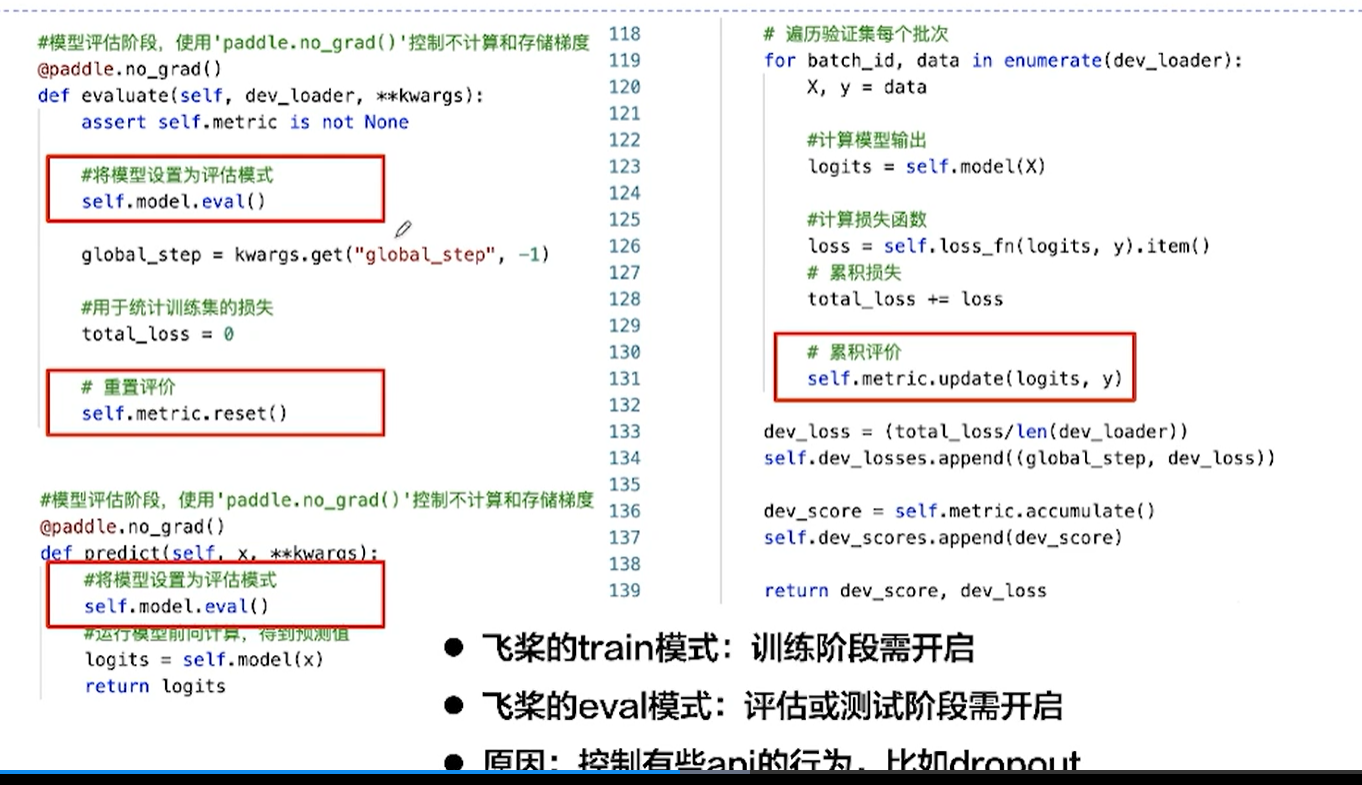
[√] D => RunnerV3

image-20221217181115279

[√] F -> RunnerV3

image-20221217181211275

[√] F -> RunnerV3 - train

image-20221217181306399

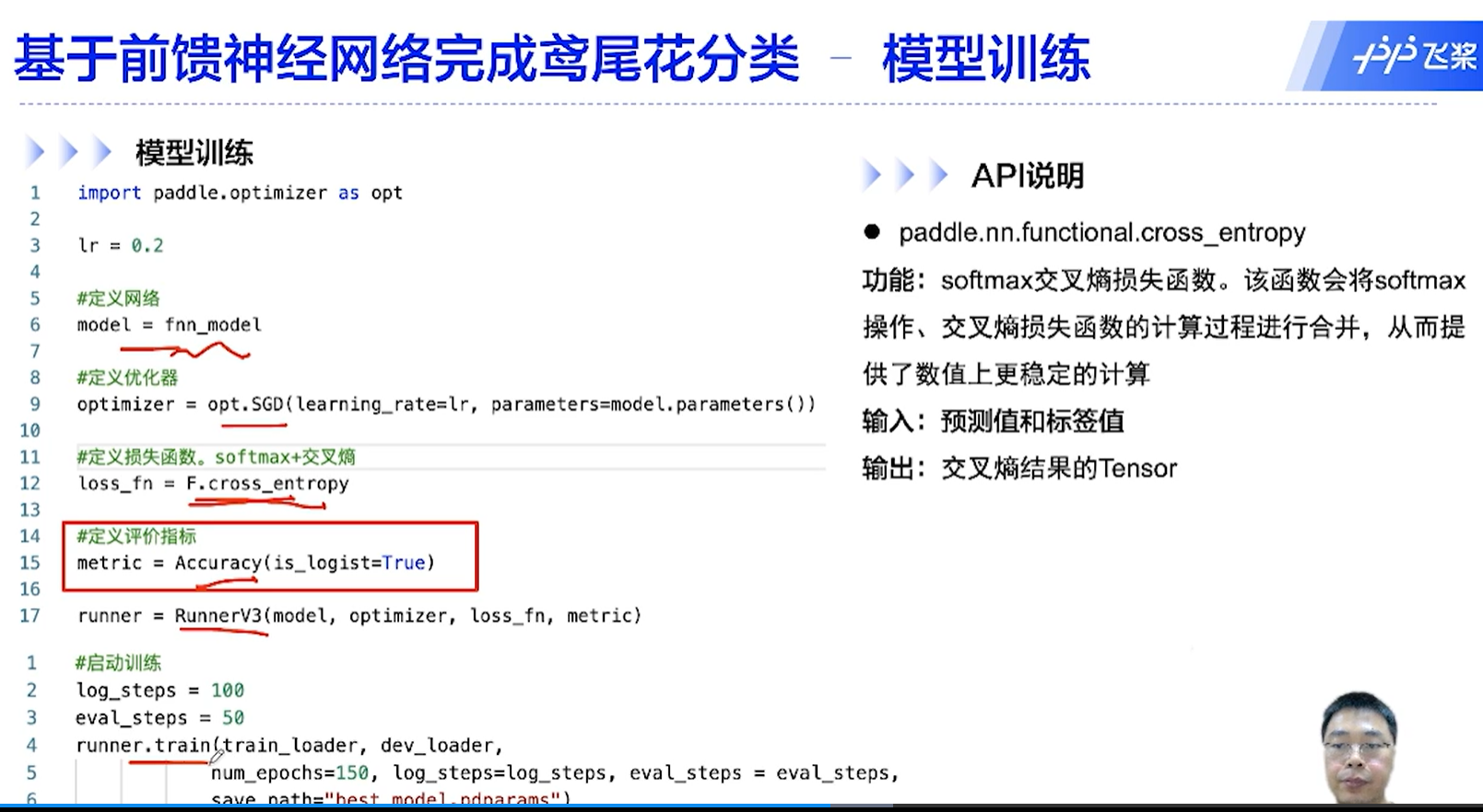
image-20221217181317314

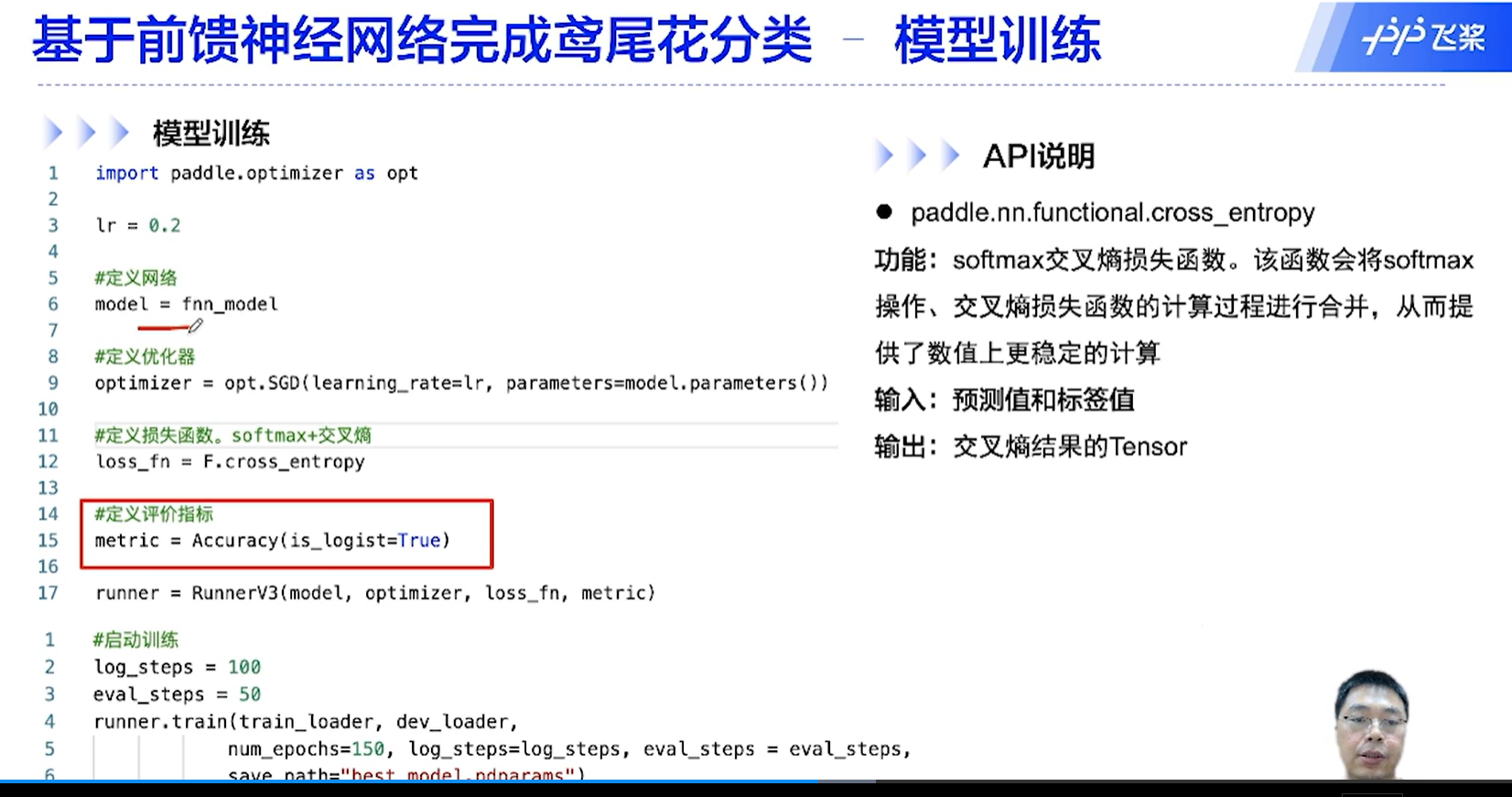
image-20221217181406357

[√] D => 模型训练

[√] F -> 模型训练

image-20221217181627593

损失函数要计算梯度、前向传播网络也要计算损失函数，损失函数只是反向传播的第一步，并不是计算了损失就可以直接进行梯度更新了，而是要计算损失，然后计算损失函数的梯度，然后从这里开始，逐层的往前计算每一层的梯度并根据链式法则计算梯度并保存，然后再根据计算的梯度来更新参数。循环往复。

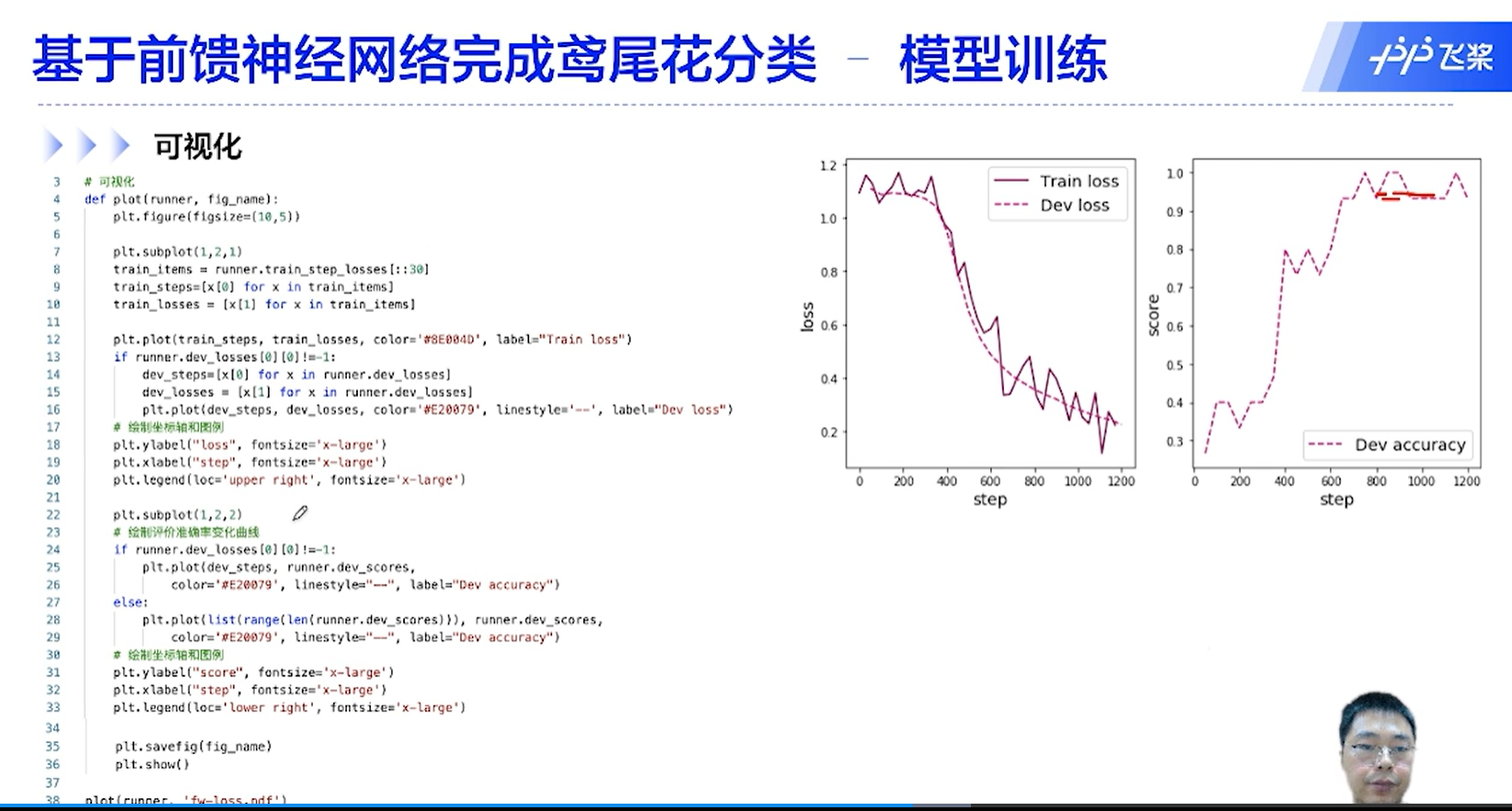
image-20221217181954787

[√] F -> 可视化

image-20221217183658601

image-20221217183719028

深度学习技术栈 > 深度学习 > 实践学习 > 神经网络与深度学习：案例与实践 - 飞桨 - 邱锡鹏
第4章 - 前馈神经网络 - 视频
https://alec-97.github.io/posts/1943031638/
作者
Shuai Zhao
发布于
2022年12月19日
许可协议