034 - 文章阅读笔记:【ENLCA】AAAI2022Efficient Non-Local Contrastive Attention for Image Super-Resolution - CSDN - 专栏:超分辨率 - hbw136
本文最后更新于:3 个月前
转载自:
于 2022-03-29 14:41:01 发表
Effificient Non-Local Contrastive Attention for Image Super-Resolution (用于图像超分辨率的高效非局部对比注意力)
[√] 论文信息
AAAI2022
作者
Shunzhou Wang1*, Tianfei Zhou2∗ , Yao Lu1† , Huijun Di1
所属组织
1 Beijing Key Laboratory of Intelligent Information Technology,
School of Computer Science and Technology, Beijing Institute of Technology, China
2 Computer Vision Laboratory, ETH Zurich, Switzerland、
论文地址:https://arxiv.org/abs/2201.03794
项目地址:https://github.com/Zj-BinXia/ENLCA
[√] 面对的问题
Non-Local Attention (NLA) 通过利用自然图像中的内在特征相关性,为单图像超分辨率 (SISR) 带来了显着的改进。
然而,NLA 赋予噪声信息很大的权重,并且相对于输入大小消耗二次计算资源,限制了其性能和应用。
alec:
- 非本地注意力NLA通过利用图像中的内在相关性,来改善超分的效果。
[√] 解决思路
在本文中,作者提出了一种新颖的高效非局部对比注意 (ENLCA) 来执行远程视觉建模并利用更多相关的非局部特征。
具体来说,ENLCA 由两部分组成,Efficient Non-Local Attention (ENLA) 和 Sparse Aggregation。
alec:
- sparse,稀疏的
- aggregation,聚合
- 稀疏聚合
ENLA采用核方法逼近指数函数,得到线性计算复杂度。对于稀疏聚合,作者将输入乘以放大因子以专注于信息特征,但近似方差呈指数增长。因此,对比学习被应用于进一步分离相关和不相关的特征。
本文的目标是聚合所有重要的相关特征,保持非局部模的稀疏性,并大大降低其计算代价。
[√] 闪光点
- 作者为 SISR 任务提出了一种新颖的高效非局部对比注(ENLCA)。ENLCA的ENLA通过核函数逼近和矩阵乘法的结合律,将计算复杂度从二次到线性显着降低。
- 此外,作者在 ENLA 上应用对比学习,以进一步加强相关特征的效果。
- ENLCA 模块可以将一个相当简单的 ResNet骨干网改进为最先进的。 大量实验证明了 ENLCA 优于标准的非局部注意 (NLA)
和非局部稀疏注意。
alec:
- NLA + 对比学习 + 稀疏聚合
[√] 具体内容
[√] 1)结构设计
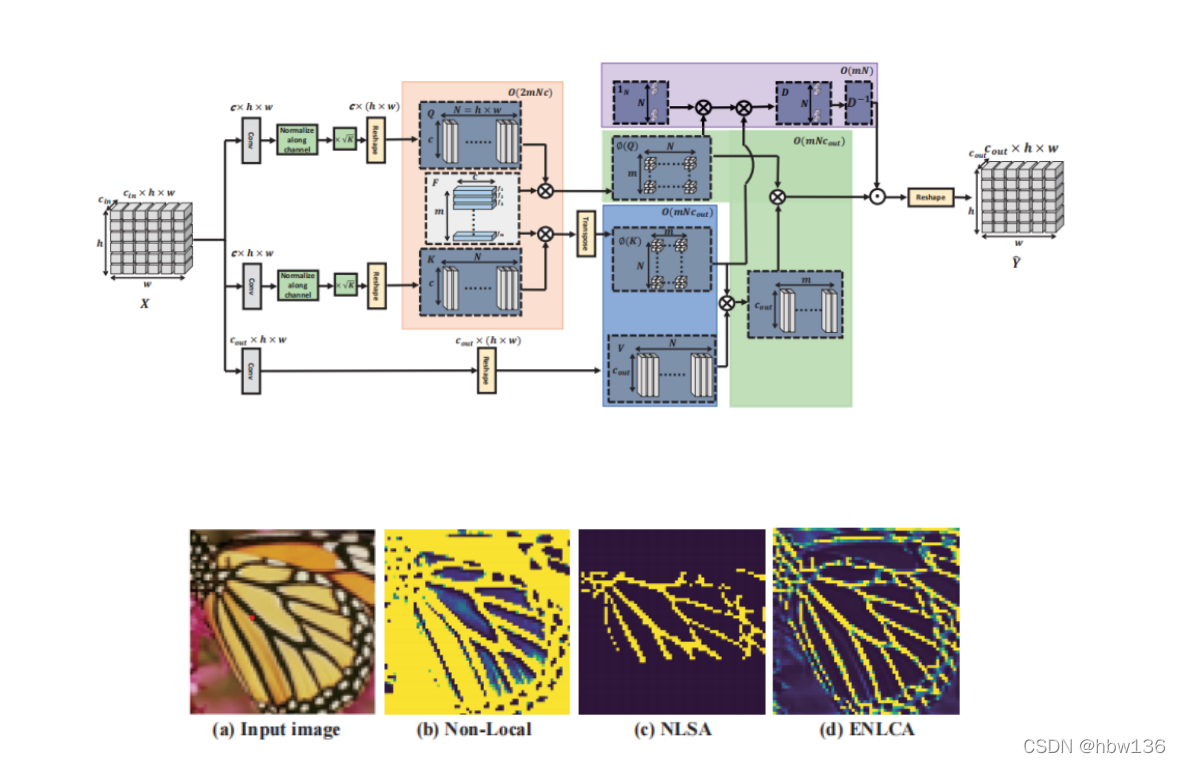
[√] 2)Non-Local Attention的一些介绍
标准非局部注意力聚合所有特征,这些特征可以将不相关的噪声传播到恢复的图像中。NLSA 通过局部敏感哈希 (LSH) 选择可能的相关特征进行聚合,较于NLA,他成功解决了不相关特征所引入的干扰,也减小了复杂度。 然而,LSH 可能会忽略有用的非局部信息,因为它只是在有限的窗口大小内粗略地利用相关信息。为了缓解这个问题,作者提出了高效的非局部注意力来有效地聚合所有特征。
[√] Non-Local Attention
非局部注意力可以通过聚合整个图像的相关特征来探索自我示例。 正式地,非局部注意力被定义为:
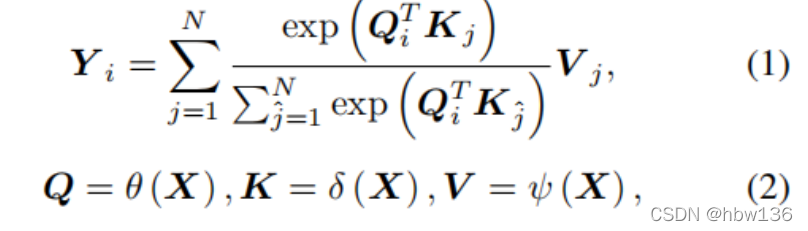
其中 Qi、Kj ∈ Rc 和 V j ∈ Rcout 分别是特征图 Q、K 和 V 上位置 i 或 j 的像素级特征。 Y i ∈ Rcout 是位置 i 的输出,X 是输入,N 是输入大小。 θ(.)、δ(.) 和 ψ(.) 是输入 X 的特征变换函数。
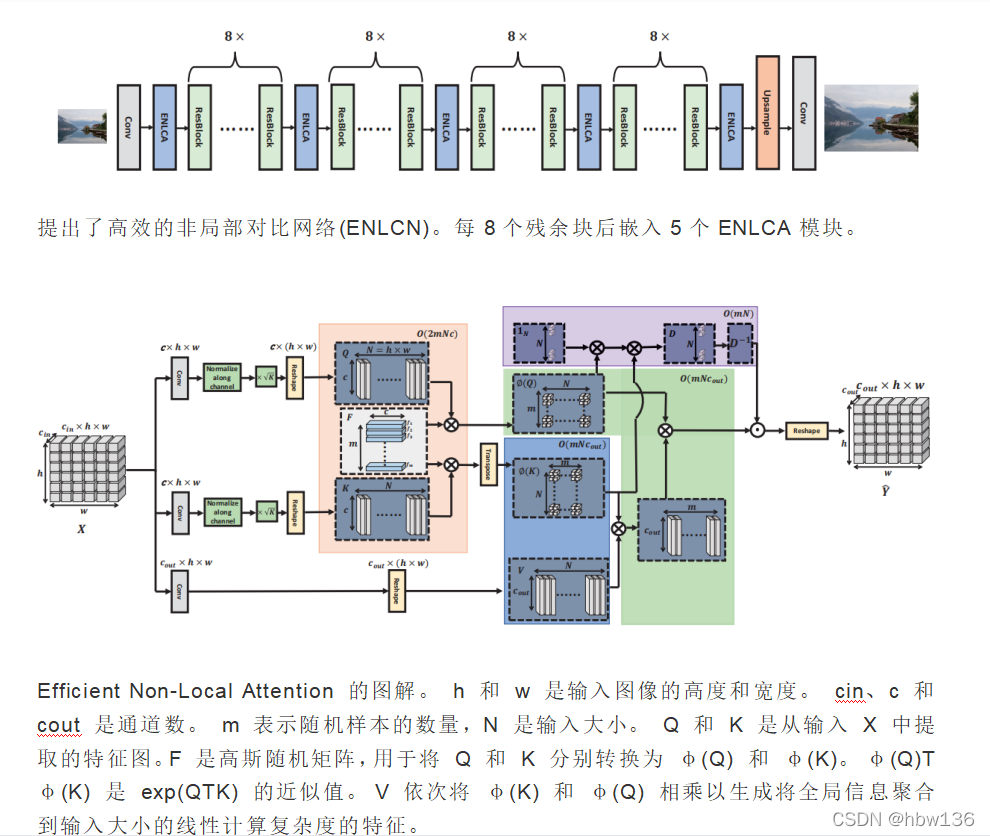
[√] Effificient Non-Local Attention
作者通过高斯随机特征近似分解exp(QTi Kj)并改变乘法顺序以获得相对于图像大小的线性复杂度。 指数核函数的分解推导如下:
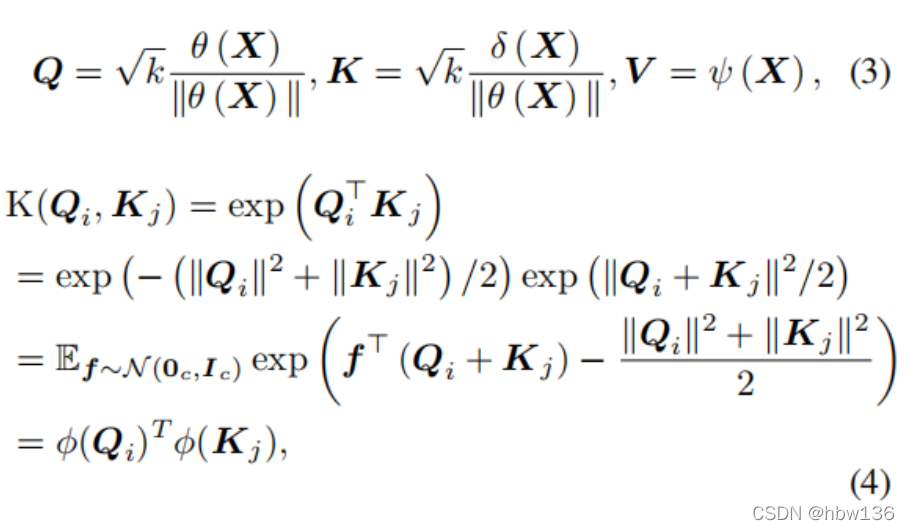
alec:
- X为输入特征图
- K为放大因子,K>1,用于增强非局部稀疏性
- θ(.),δ(.),和ψ(.)都是特征转换
Qi和Kj∈Rc是特征图Q和K∈Rc×N上的位置i或j处的像素级特征。f∈Rc和f∼N(0c,Ic)。
基于上述推断,作者提出的注意力可以被表示为:
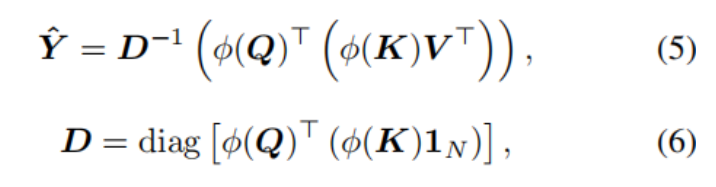
其中,Yˆ代表近似的标准非局部注意,D是softmax操作符中的归一化项目,括号表示计算的顺序。
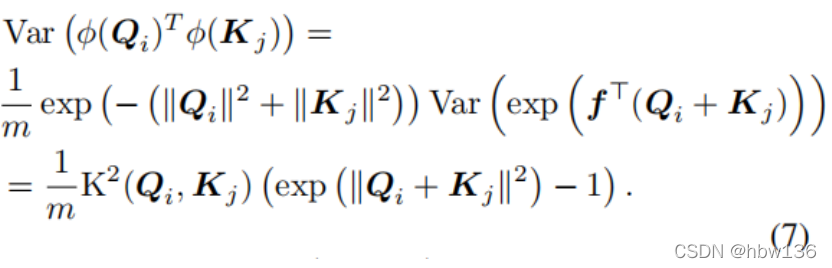
因此,随着K(Qi、Kj)的增加,φ(Qi)Tφ(Kj)的方差呈指数级增长。为了保证近似结果的准确性,不可能将K(Qi,Kj)乘以一个较大的放大因子k。此外,保持高斯随机样本的正交可以减少近似方差。
[√] 3)稀疏聚合
为了进一步提高有效非局部注意的性能,作者过滤掉了无关信息,扩大了相关信息的权重。
直观地说,将输入乘以放大因子 k(k > 1) 可以强制非局部注意力在相关信息上赋予更高的聚合权重,其本质是增强非局部注意力权重的稀疏性。 不好的是,乘以放大因子 k(k > 1) 会导致 ENLA 近似方差的增加。
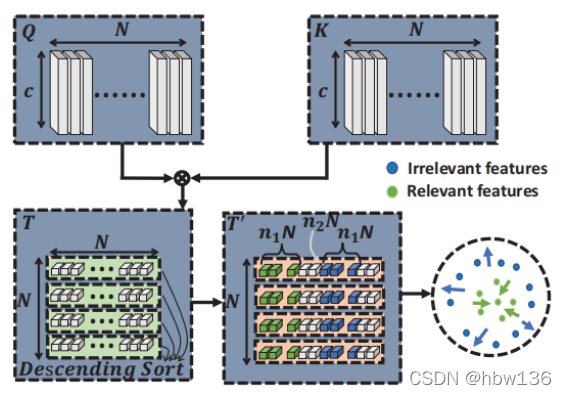
上图为作者的ENLCA对比学习方案的图示。对于每个有序序列,作者将前n1n个相关特征作为相关特征,将从n2n开始的n1n个不相关特征作为不相关特征。
为了缓解这个问题,作者通过应用对比学习进一步开发了高效的非局部对比注意 (ENLCA)。 采用对比学习的目标是增加不相关和相关特征之间的差距。 如图 4 所示,用于训练 ENLCA 的对比学习损失 Lcl 可以表示为:
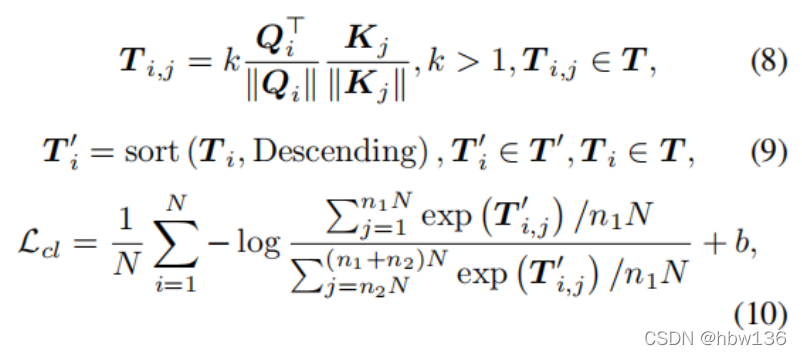
其中,N表示输入的大小。B是一个边际常数。n1表示特征图中相关特征和无关特征的百分比,n2分别为特征图中不相关特征的起始索引百分比。Ti、j用归一化的内积来衡量Qi和Kj之间的相关性。Ti和T0i分别表示T和T0∈RN的第i行×N。另外,t’i是ti的降序排序结果。
因此,作者的模型的整体损失函数最终被设计为:
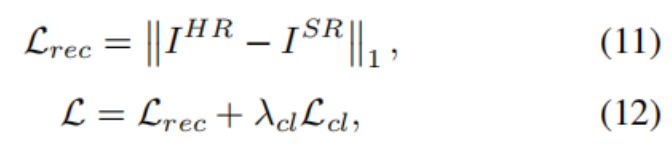
[√] 4)实验设置
训练数据集作者使用 DIV2K ,一个包含 800 个训练图像的数据集来训练作者的模型。 作者在 5 个标准 SISR 基准上测试作者的方法:Set5、Set14、B100、Urban100和 Manga109。 作者仅在转换后的 YCbCr 空间中通过 Y 通道上的 PSNR 和 SSIM 指标评估所有 SR 结果。
对于 ENLCA,作者在每个 epoch 重新生成高斯随机矩阵 F。 此外,放大因子 k 为 6,margin b 为 1。随机样本数 m 设置为 128。作者使用 EDSR 主干构建 ENLCN,其中包含 32 个残差块和 5 个附加 ENLCA 块。 网络中的所有卷积核大小都是 3 × 3。所有中间特征都有 256 个通道,除了注意力模块中的嵌入特征有 64 个通道。 最后一个卷积层有 3 个filter,用于将特征图转换为 3 通道 RGB 图像。
在训练期间,作者将对比学习的 n1 和 n2 分别设置为 2% 和 8%。 此外,作者从 16 幅图像中随机裁剪 28 × 28 和 46 × 46 块,分别形成 ×4 和 ×2 SR 的输入批次。 作者通过随机水平翻转和旋转 90°、180°、270° 来增加训练块。 该模型由 ADAM 优化器 (Kingma and Ba 2014) 优化,β1 = 0.9,β2 = 0.99,初始学习率为 1e-4。 作者在 200 个 epoch 后将学习率降低 0.5,并在 1000 个 epoch 后获得最终模型。 作者首先通过仅使用 Lrec 训练 150 个 epoch 来预热网络,然后使用所有损失函数进行训练。
[√] 5)结果对比
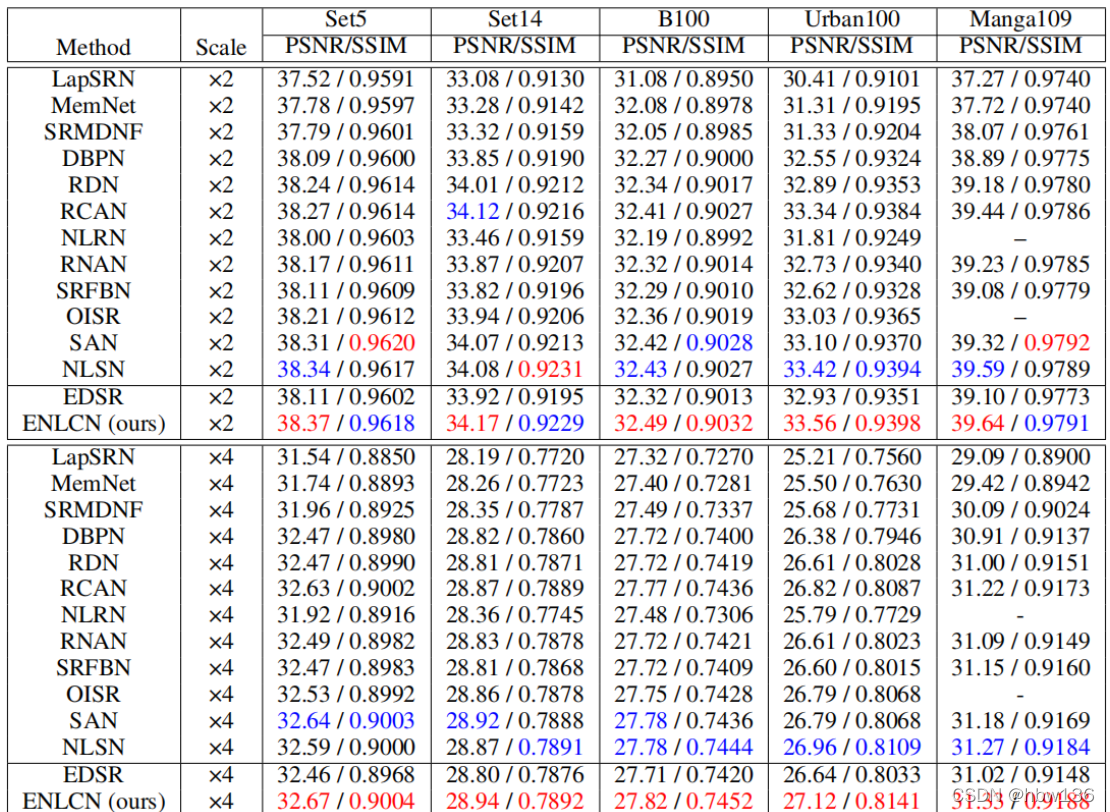
比例因子(scale) ×2 和 ×4 的定量比较。 与其他方法相比,作者的 ENLCN 在几乎所有基准和所有比例因子上都取得了最好的结果。 值得注意的是,添加额外的 ENLCA 带来了显着的改进,甚至驱动主干 EDSR 的性能优于最先进的方法,例如 SAN 和 RCAN。 具体来说,与 EDSR 相比,ENLCN 在 Set5、Set14 和 B100 中提高了约 0.2 dB,而在 Urban100 和 Manga109 中提高了约 0.5 dB。 此外,与以前的基于非局部的方法(如 NLRN 和 RNAN)相比,作者的网络在性能上表现出巨大的优势。 这主要是因为 ENLCA 只关注相关特征的聚合,并从不相关的特征中过滤掉噪声信息,从而产生更准确的预测。 此外,与 NLSN 等基于稀疏非局部注意 (NLSA) 的方法相比,作者的 ENLCN 在几乎所有环境中都体现了进步。

在Urban100数据集上对4×SR的视觉比较。对于所有显示的示例,作者的方法明显优于其他最先进的技术,可以看到特别是在富含重复纹理和结构的图像中。
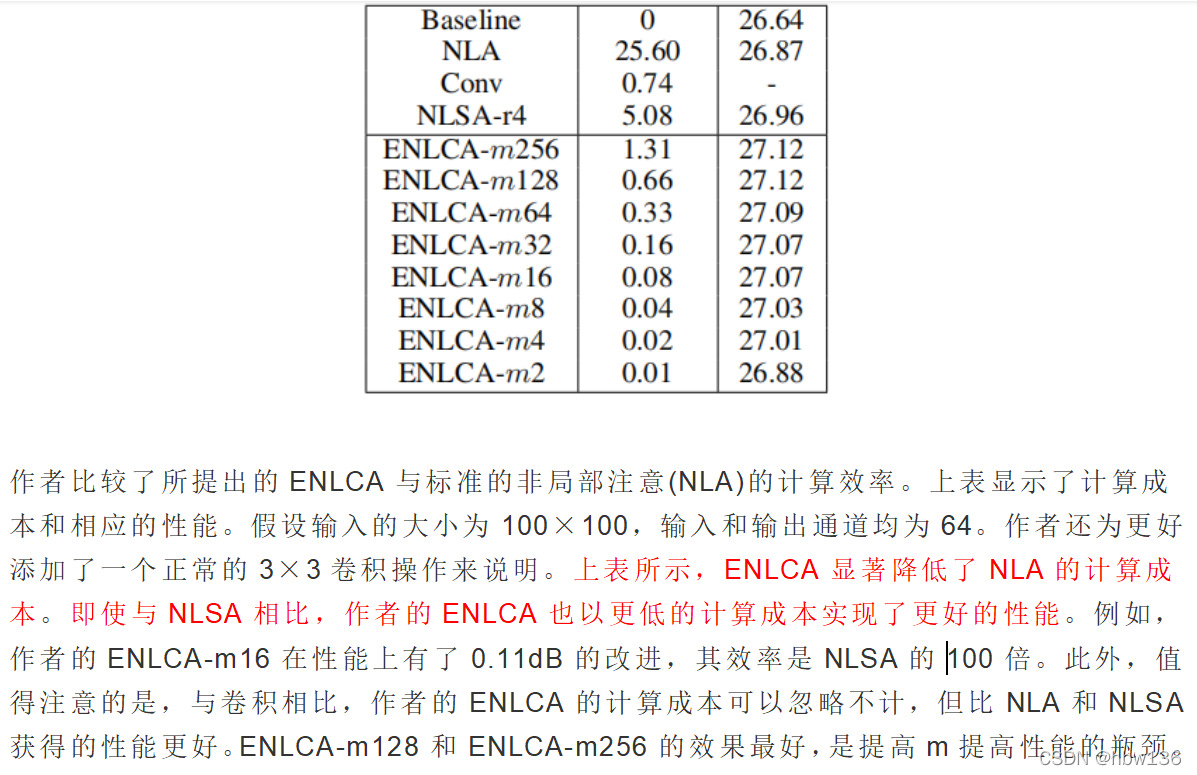
[√] 6)消融实验
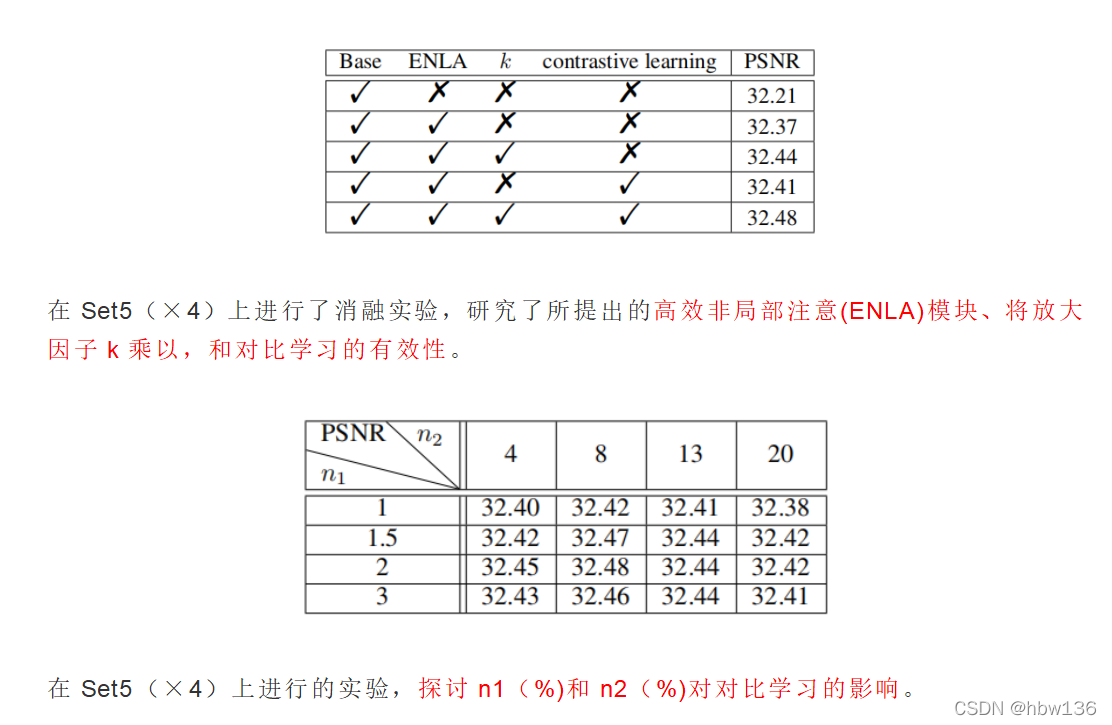
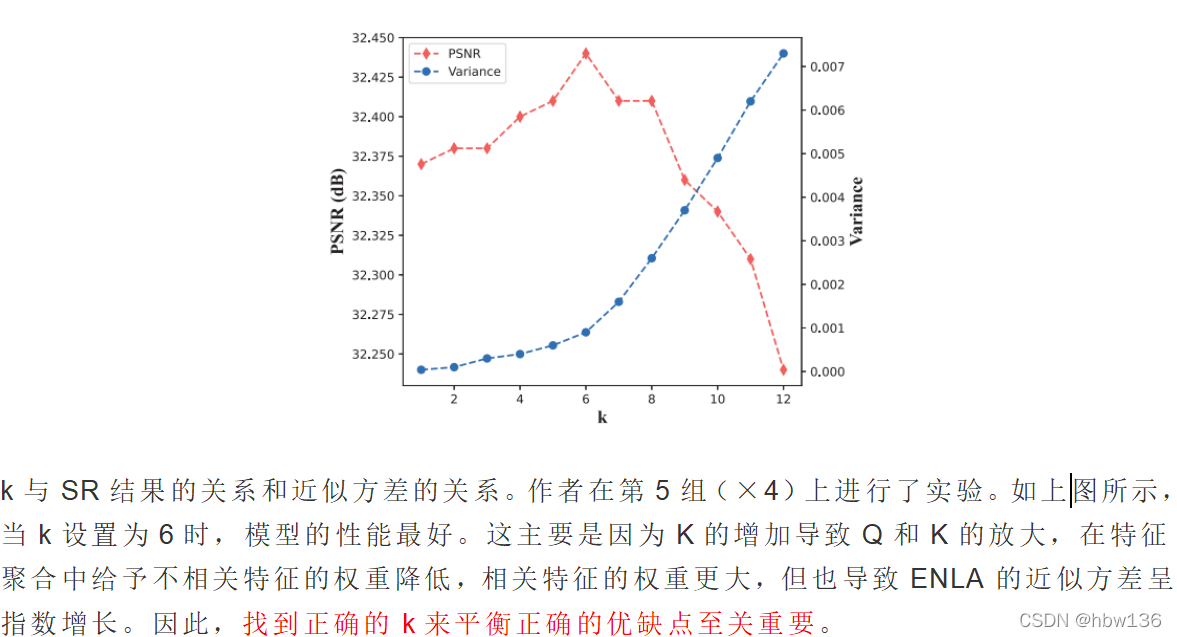
alec:
- 注意力机制中,将QK计算到的注意力,乘以放大因子k,可以提高注意力,找到一个合适的注意力放大因子K对于最终的效果是非常有益的
[√] 启发
1·所提出的Effificient Non-Local Attention部分较传统NLSA不仅性能有所提升执行效率也得到很大的提升,可以拿enlca替换掉nlsa的部分以获取提升。
2·所利用的对比学习的思想也给作者的网络带了提升,它可以有效区分相关与不相关的特征,以增强非局部注意力权重的稀疏性,但注意这会导致近似方差的增加(variance)。