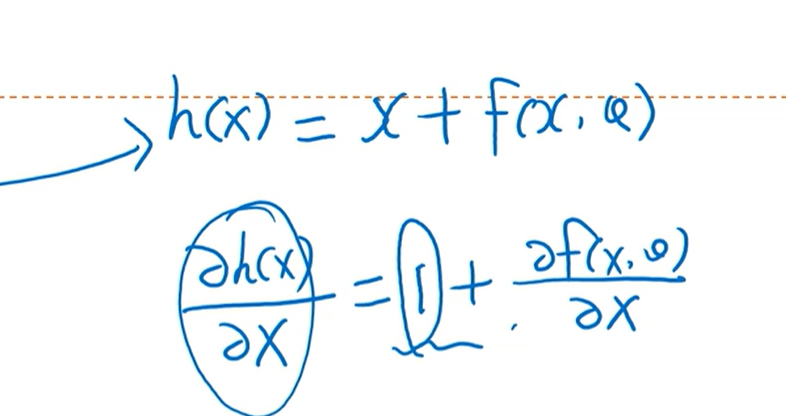5 - 卷积神经网络
本文最后更新于:3 个月前
[√] 5 - 课节5:卷积神经网络
[√] 5.0 - 卷积神经网络概述
卷积神经网络的信息也是单向传递的
[√] 全连接前馈神经网络
alec:
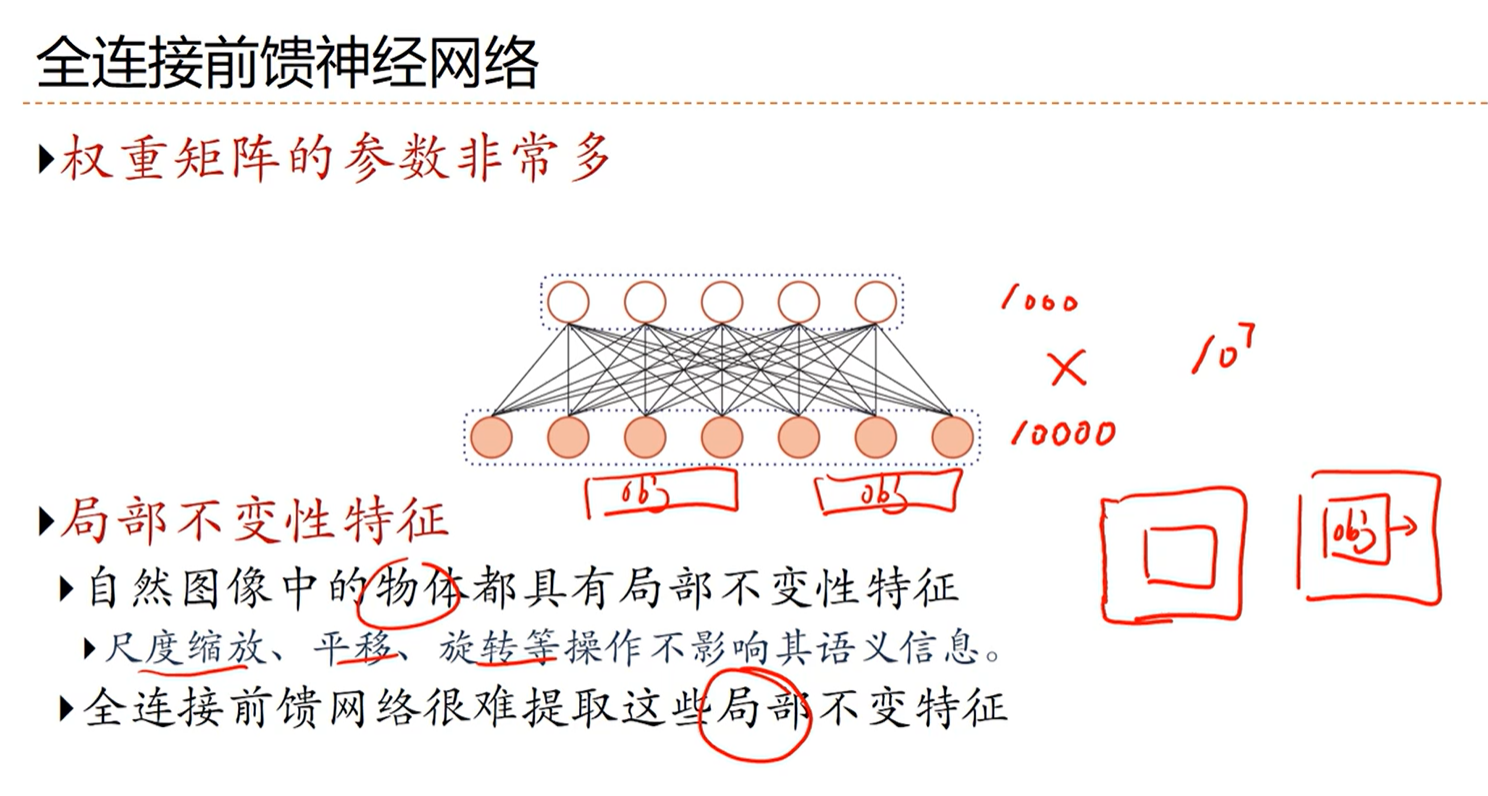
全连接很难提取图像上局部不变的特性
图像上的一些特征是平移、旋转、缩放等不变的
[√] 卷积神经网络

[√] 本章内容

[√] 5.1 - 卷积
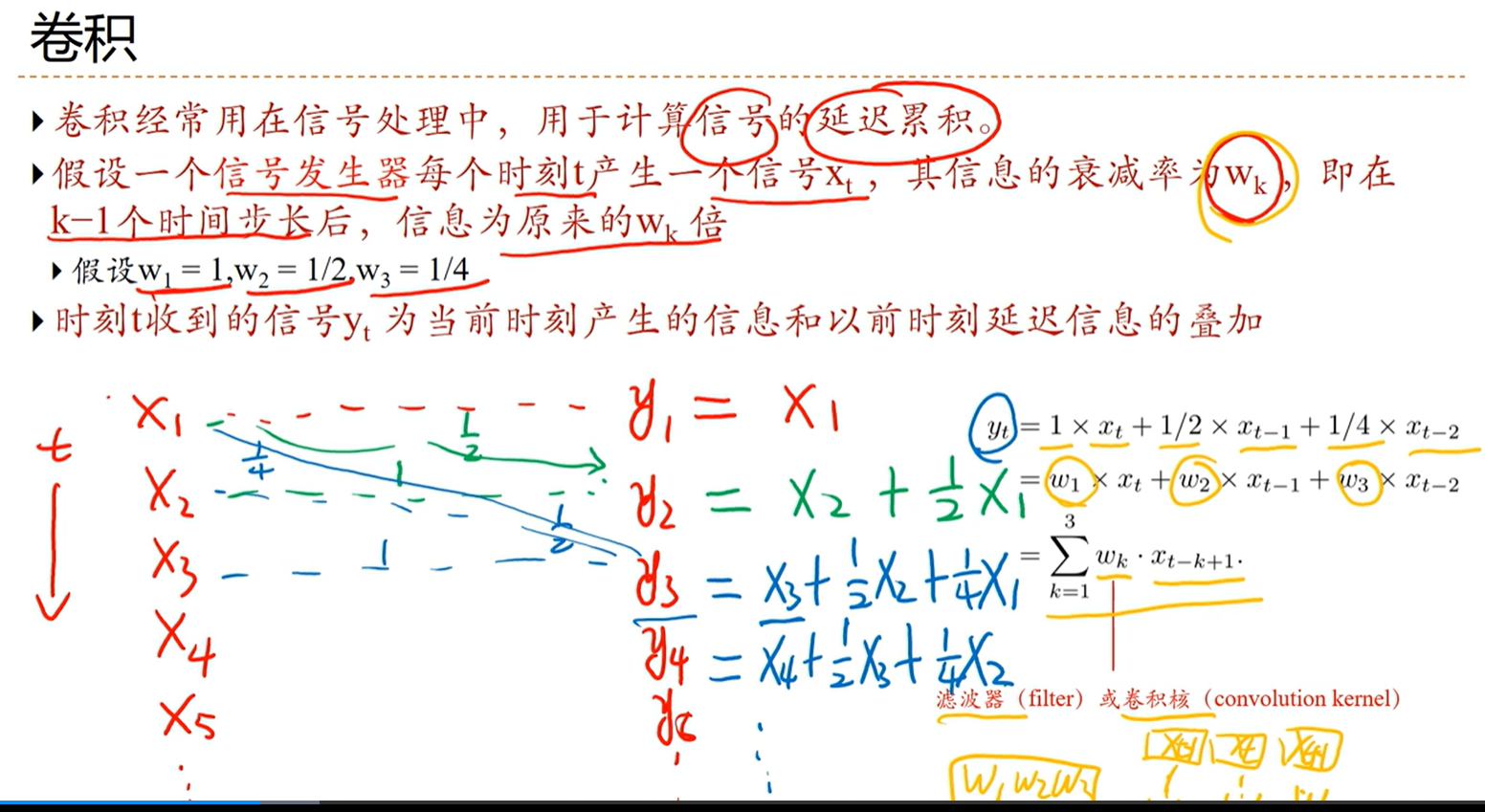
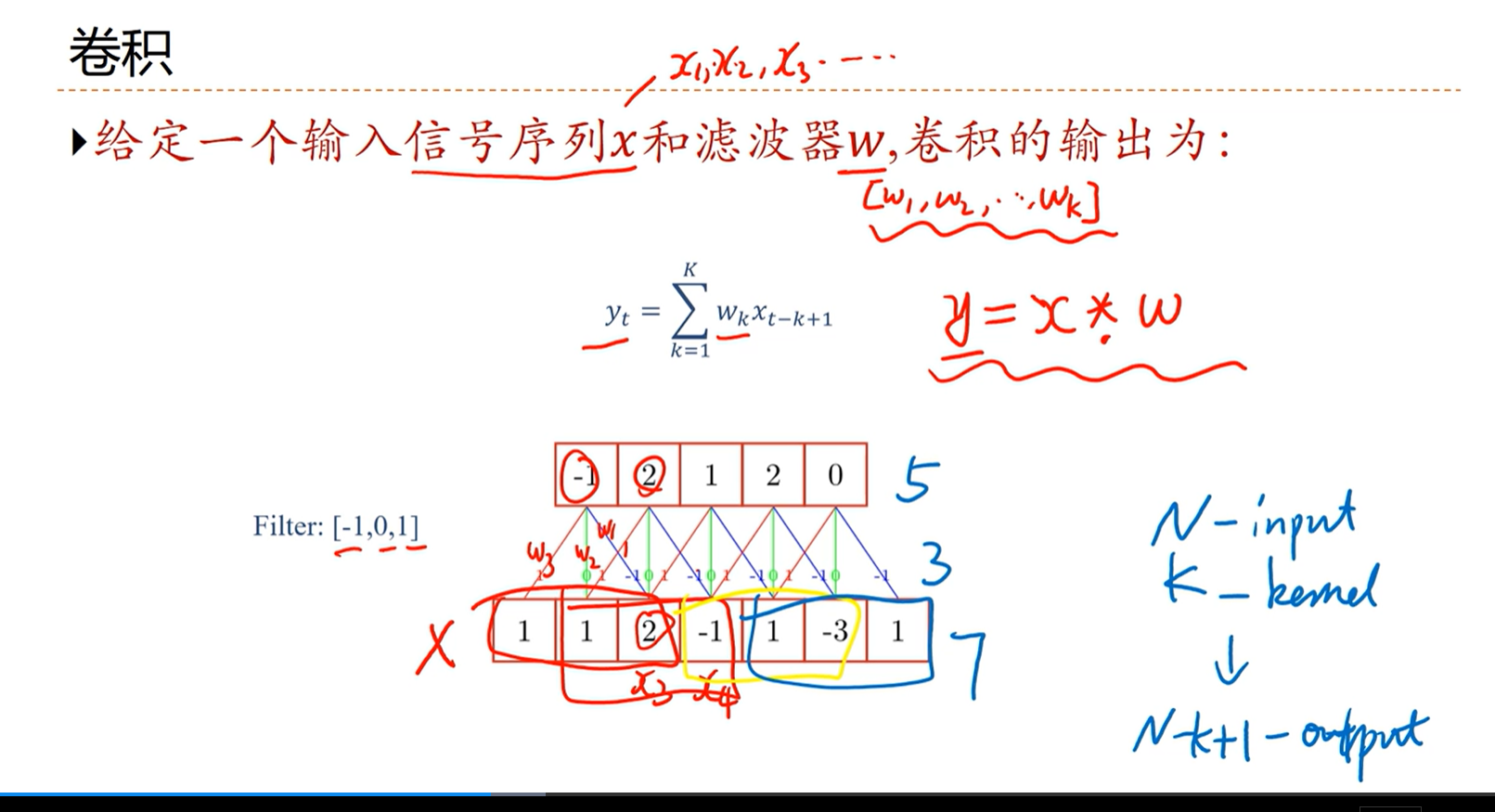
——>[√] 卷积
alec:
卷积输出的长度为:N-K+1,N为数据长度、K为滤波器长度、
——>[√] 卷积的作用
——>[√] 近似微分

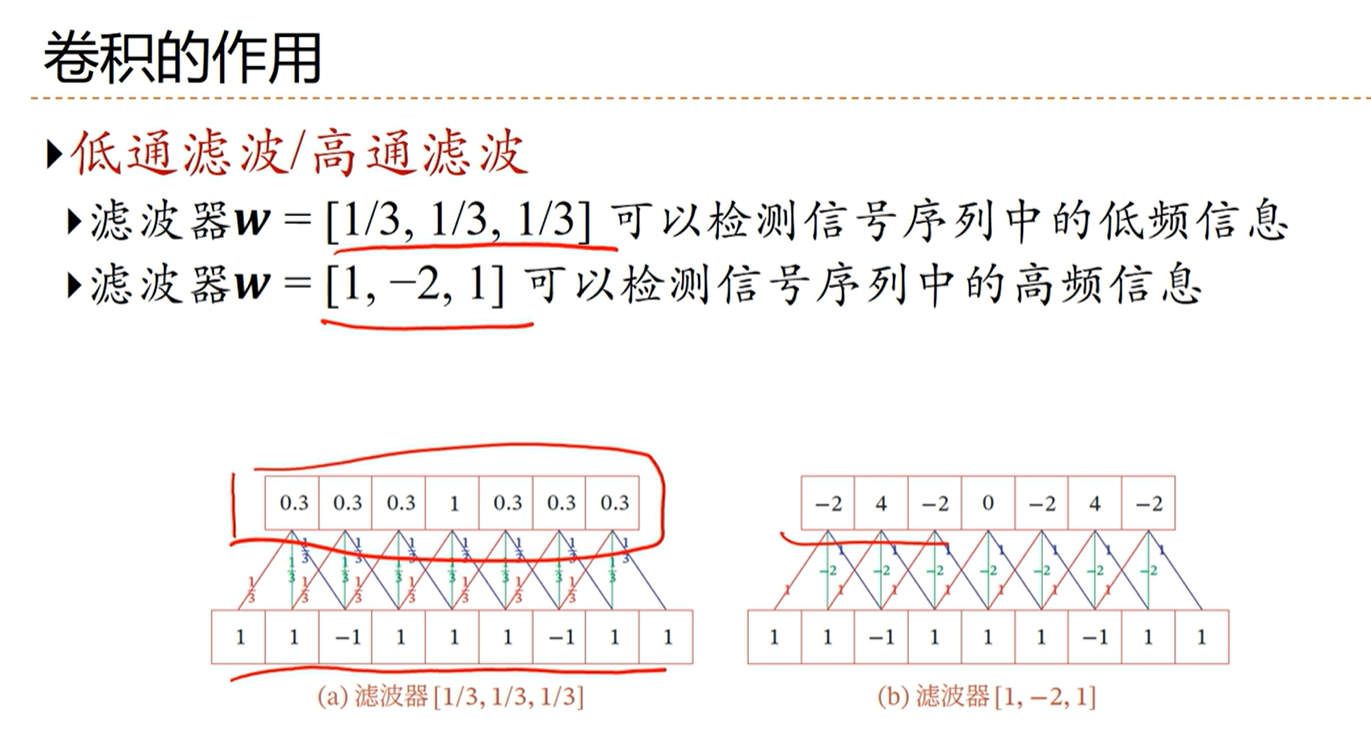
——>[√] 低通滤波/高通滤波
——>[√] 卷积扩展
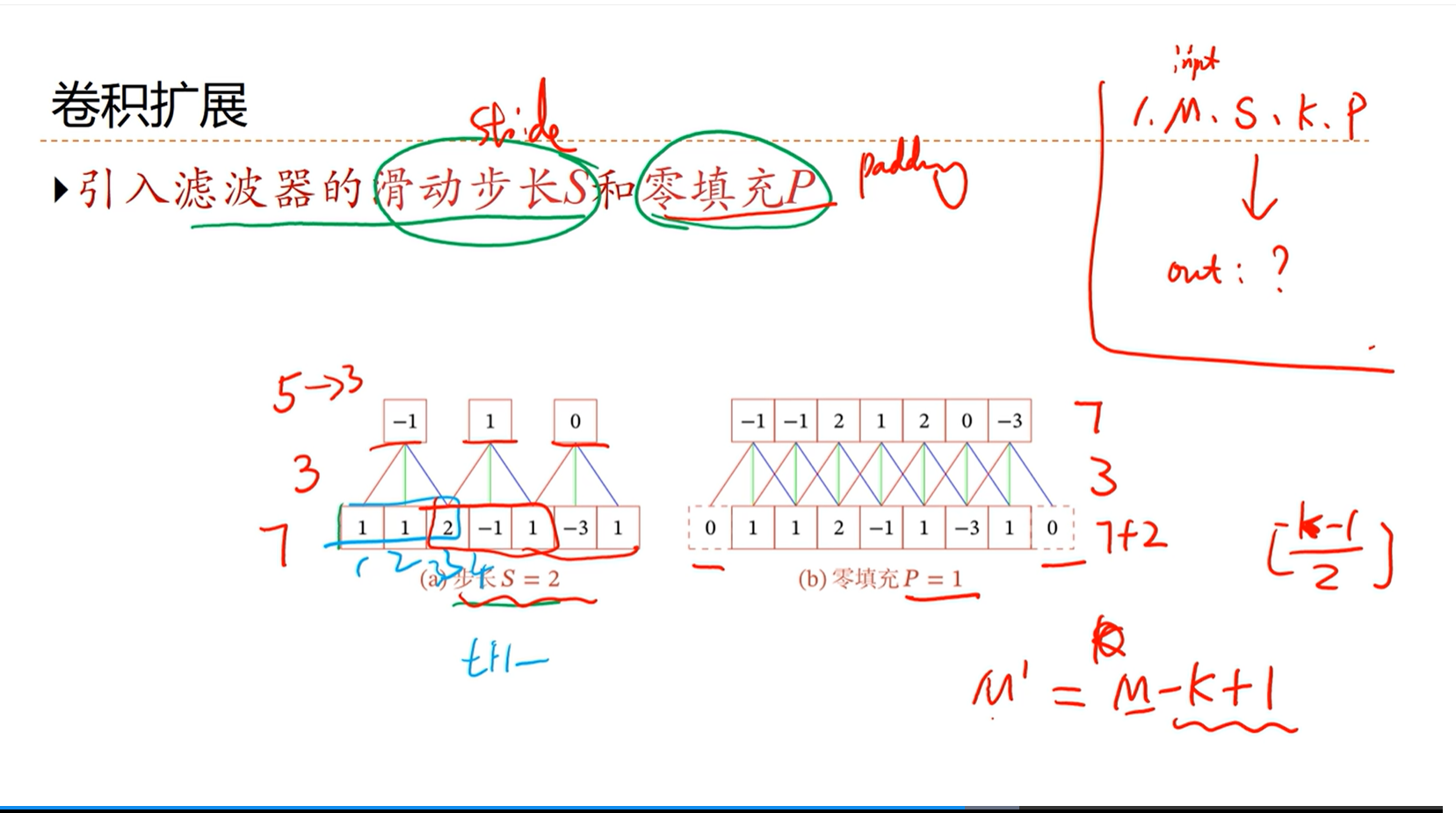
alec:
当想要卷积后尺寸不变的话,那么padding的长度为(k-1)/ 2,其中k为卷积核的长度
卷积输出的长度为:
L = (M+2P-K)/ 2 + 1
——>[√] 卷积类型

——>[√] 二维卷积
alec:
将M-K+1记为1+M-K简单一些
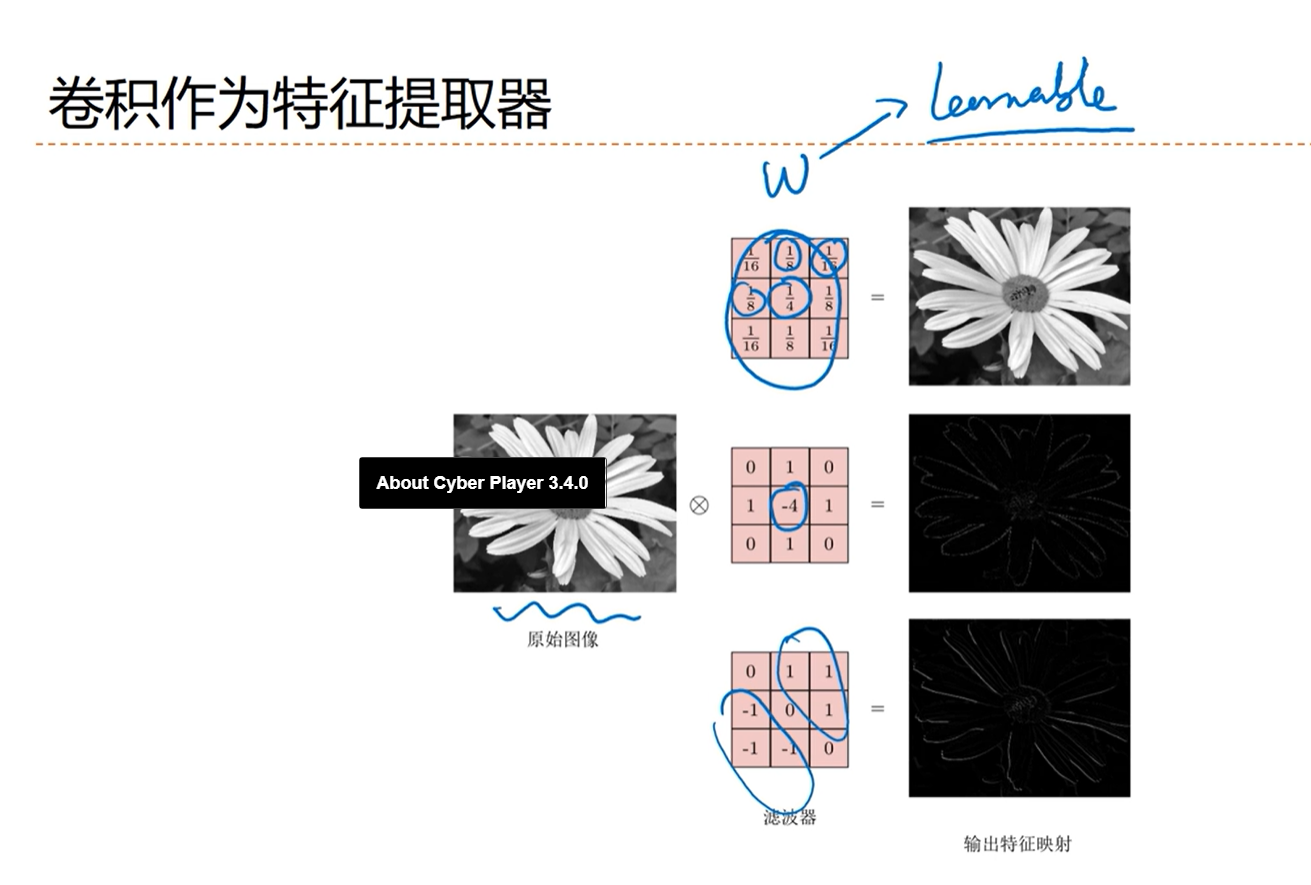
——>[√] 卷积作为特征提取器
alec:
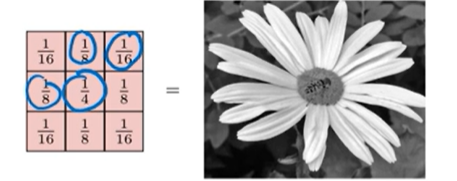
高斯滤波可以去噪,卷积核用周围点的信息来平均当前点的信息,使得图像更加的光滑
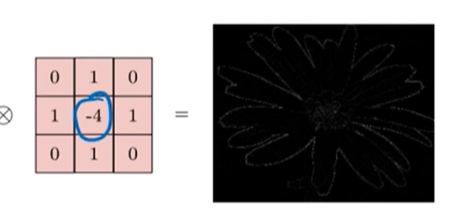
提取高频信息
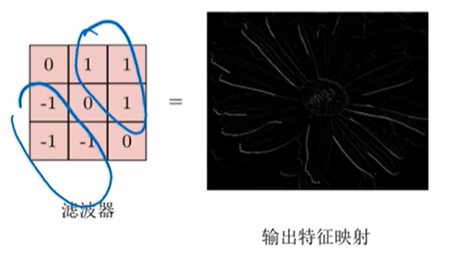
针对性的提取有方向的边缘
[√] 5.2 - 卷积神经网络
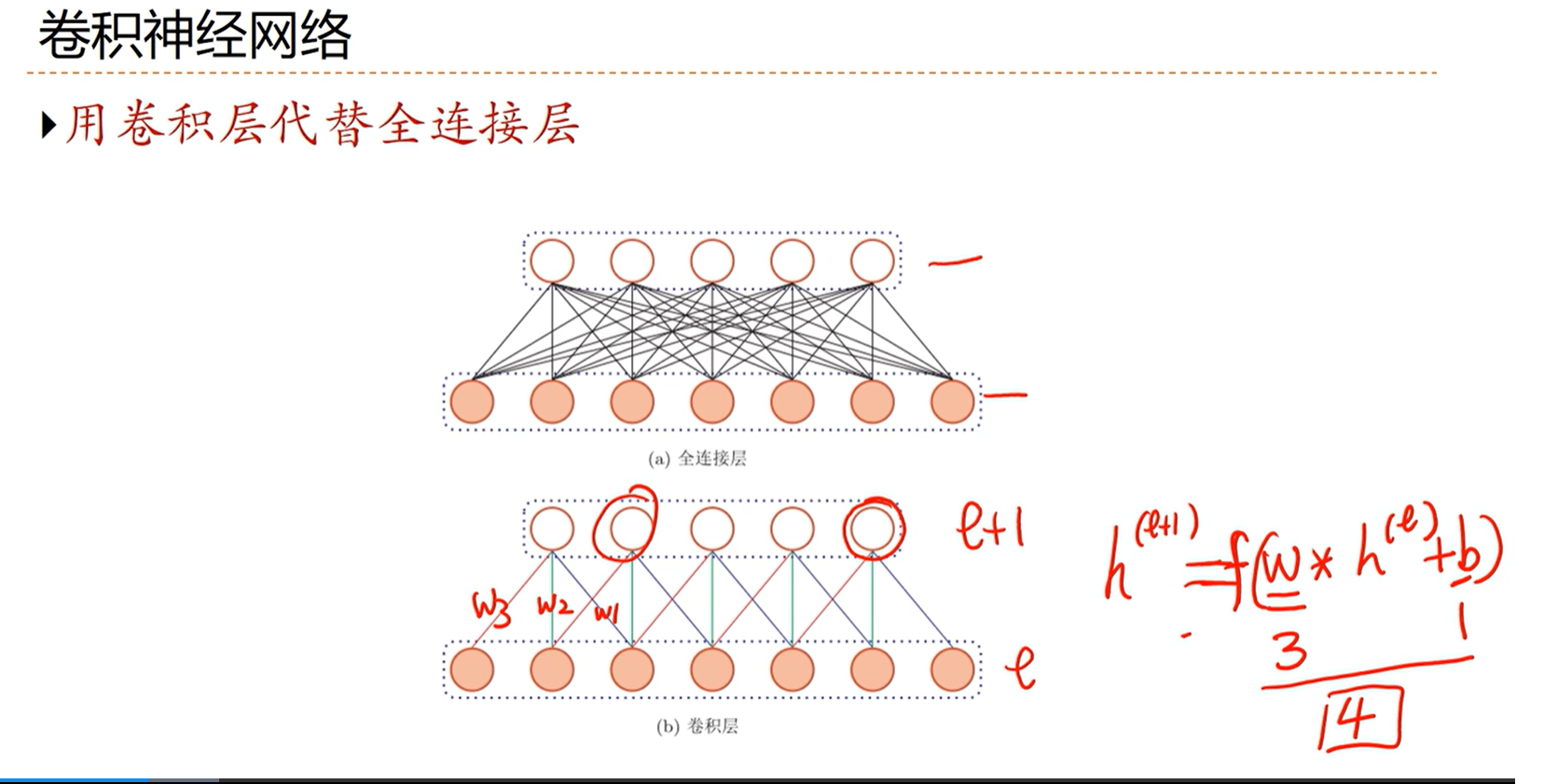
[√] 卷积神经网络
alec:
- 全连接中,下一层的一个神经元信息是收集的前一层的所有神经元的信息
- 卷积中,下一层的一个神经炎信息是收集的在前一层,卷积核当前所在位置对应的神经元信息的信息。即只收集了局部信息。
- 卷积特性:在不同位置的上的参数都是相等的,因此参数量大大减小,且共享权重
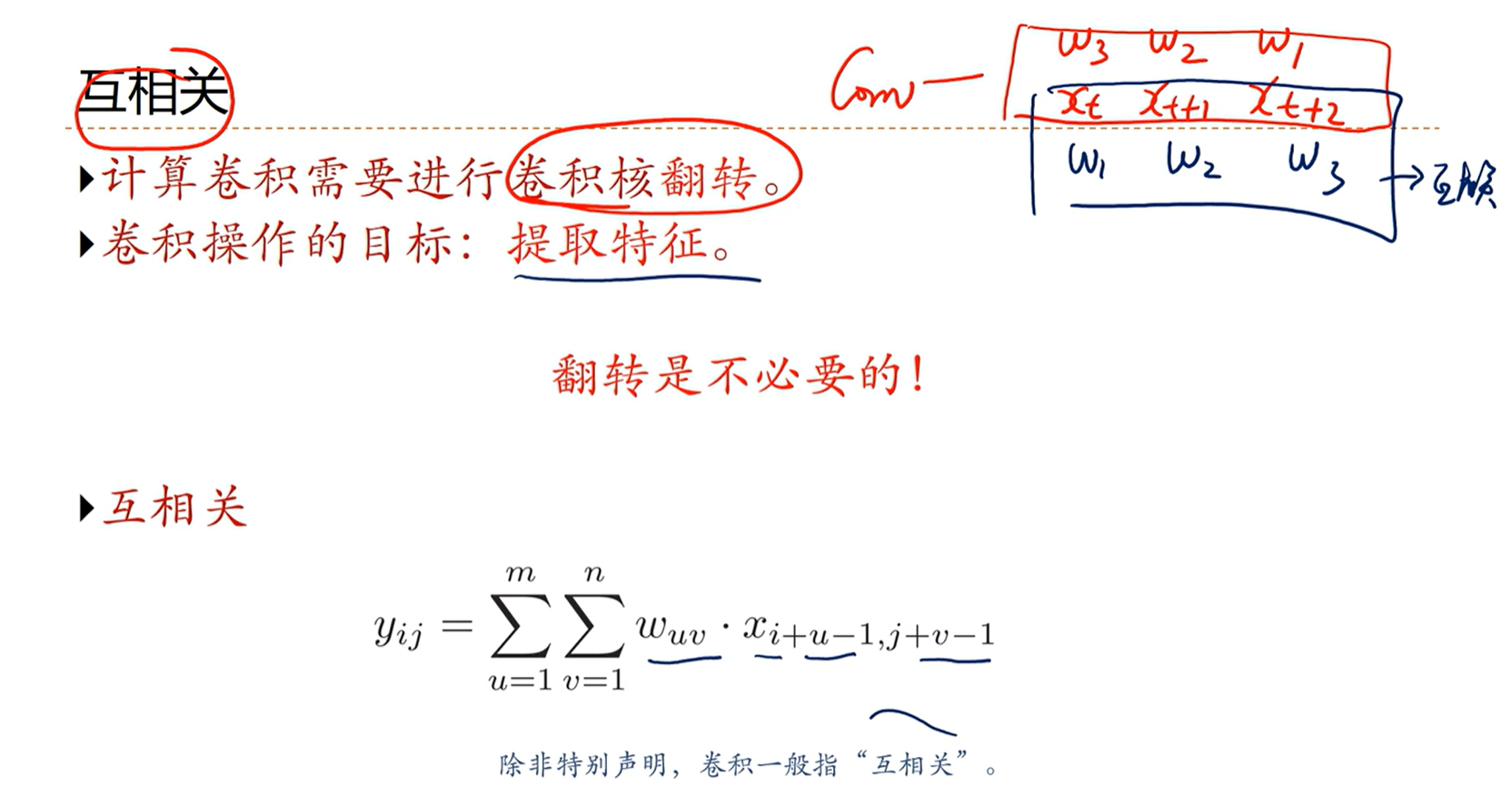
[√] 互相关
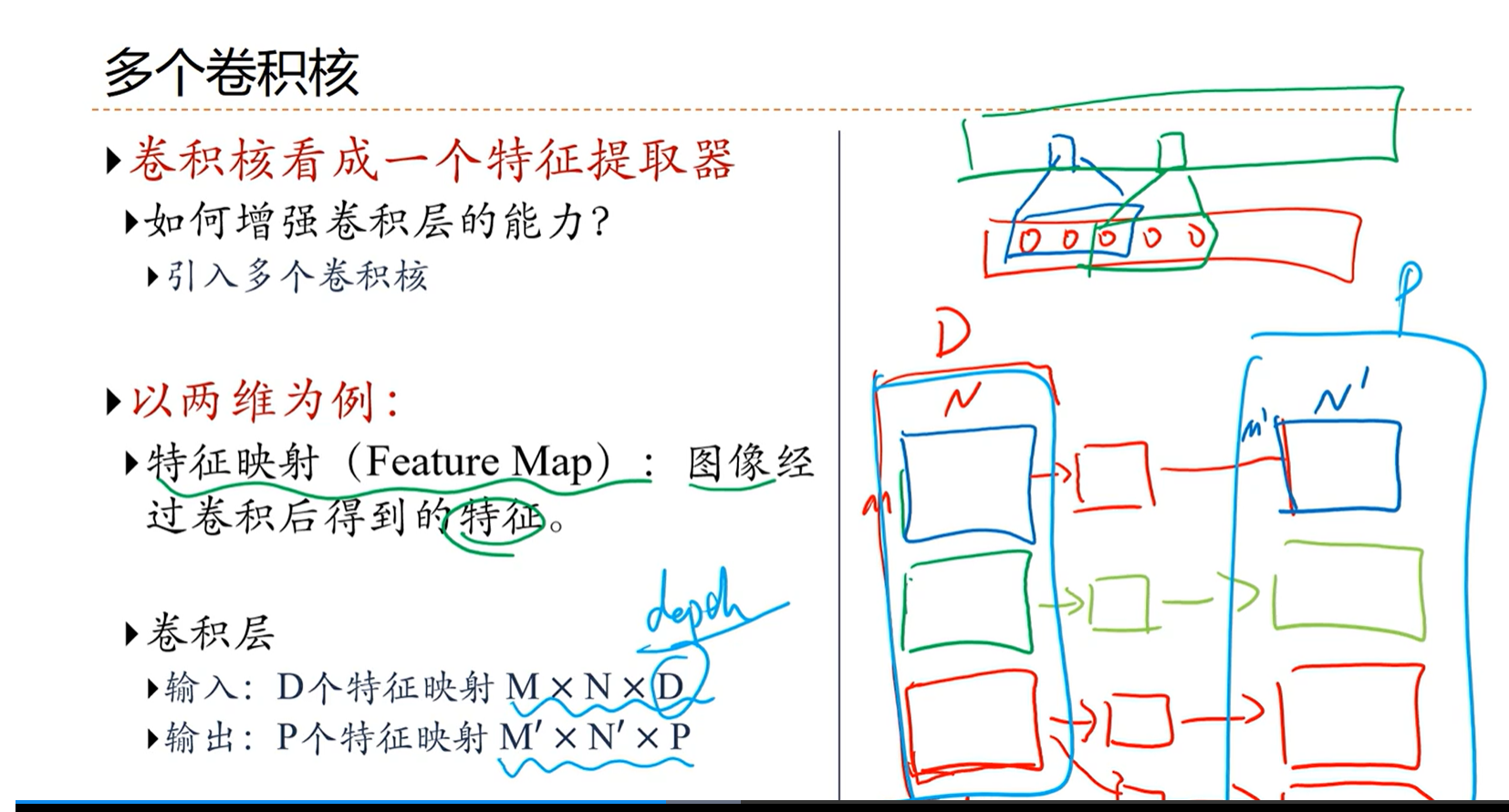
[√] 多个卷积核
alec:
单个卷积的参数量非常少,因此很自然的能力就会下降
因此通过在一层放多个卷积核,提取不同的特征,来提高网络的能力
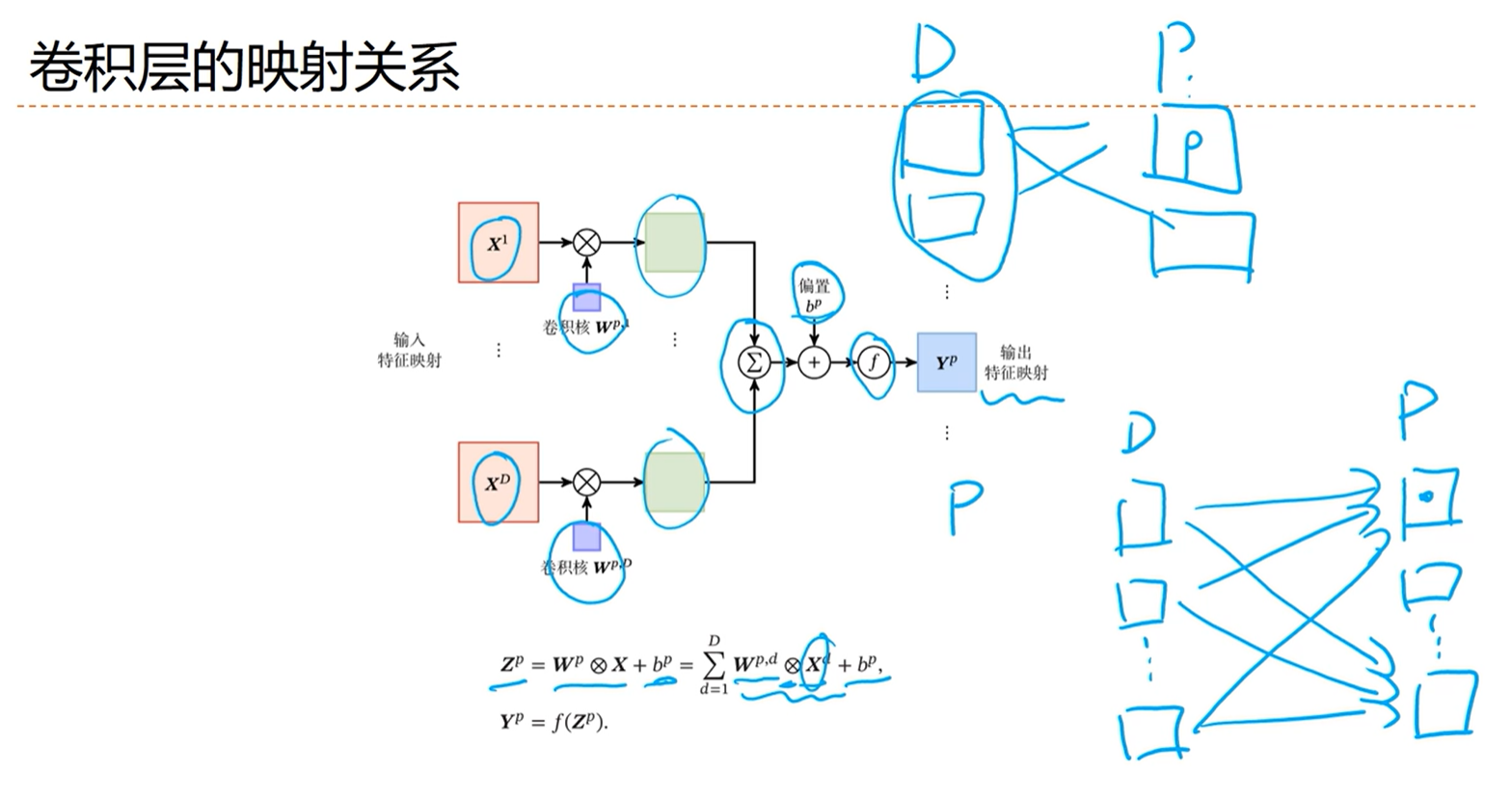
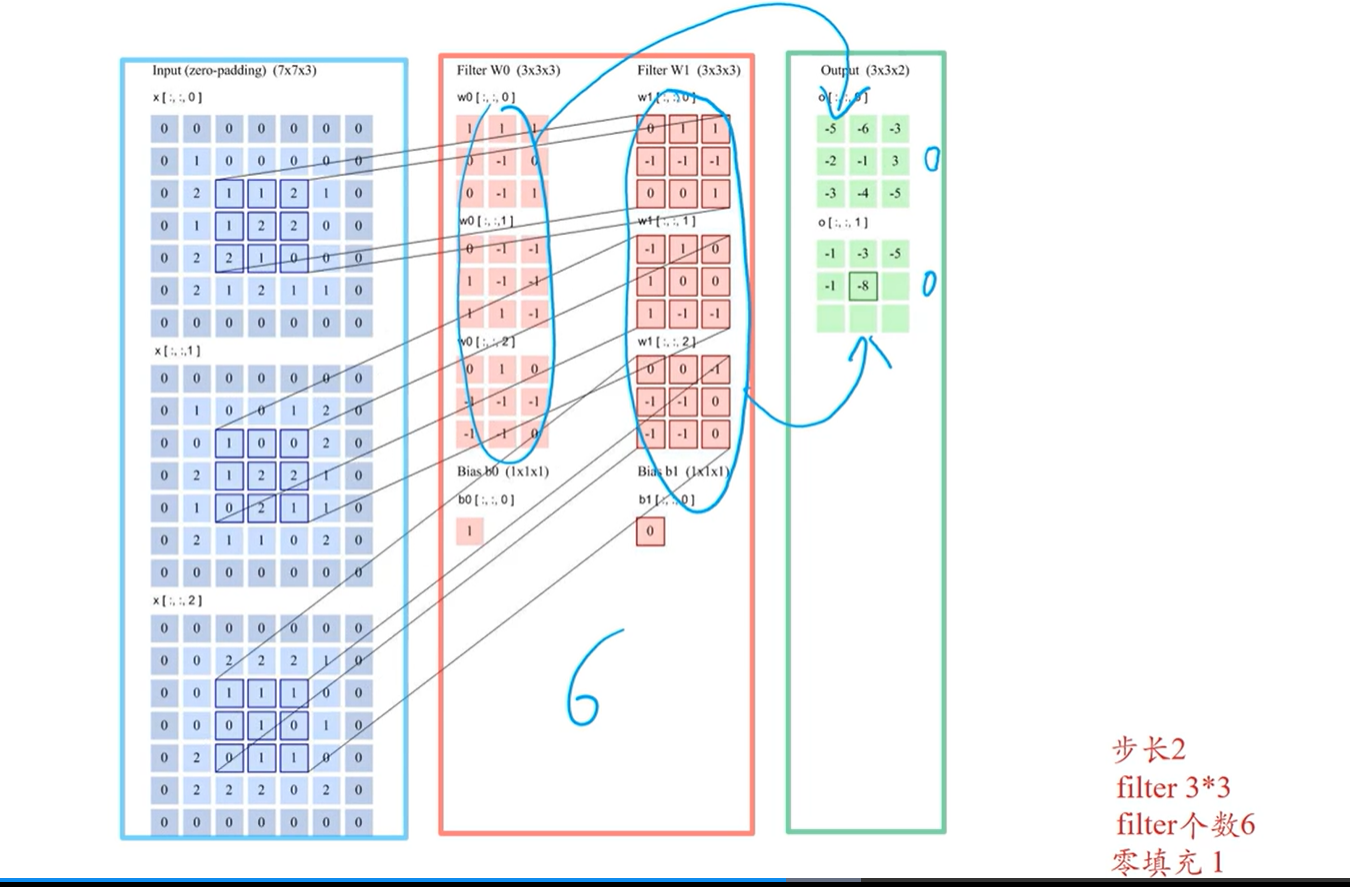
[√] 卷积层的映射关系
alec:
三个通道对应三组卷积核,每组卷积核中的卷积核不一定是相等的
[√] 卷积层
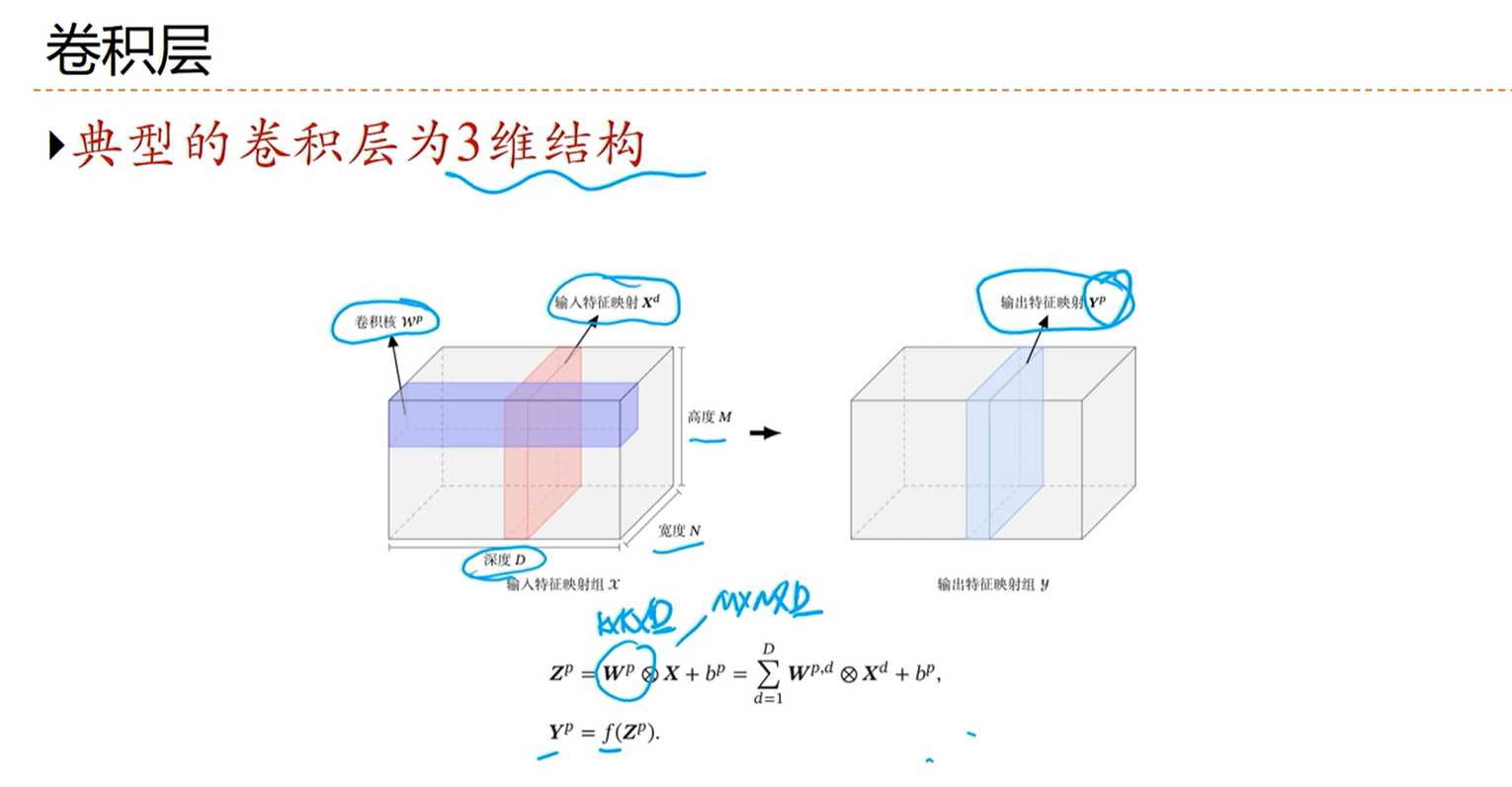
[√] 汇聚层
alec:
- 卷积层只是减少了连接的个数,但是神经元的个数并没有显著减少,下一层的神经元的个数是1+(M+2P-K)/ S
- 引入汇聚层减少神经元的个数
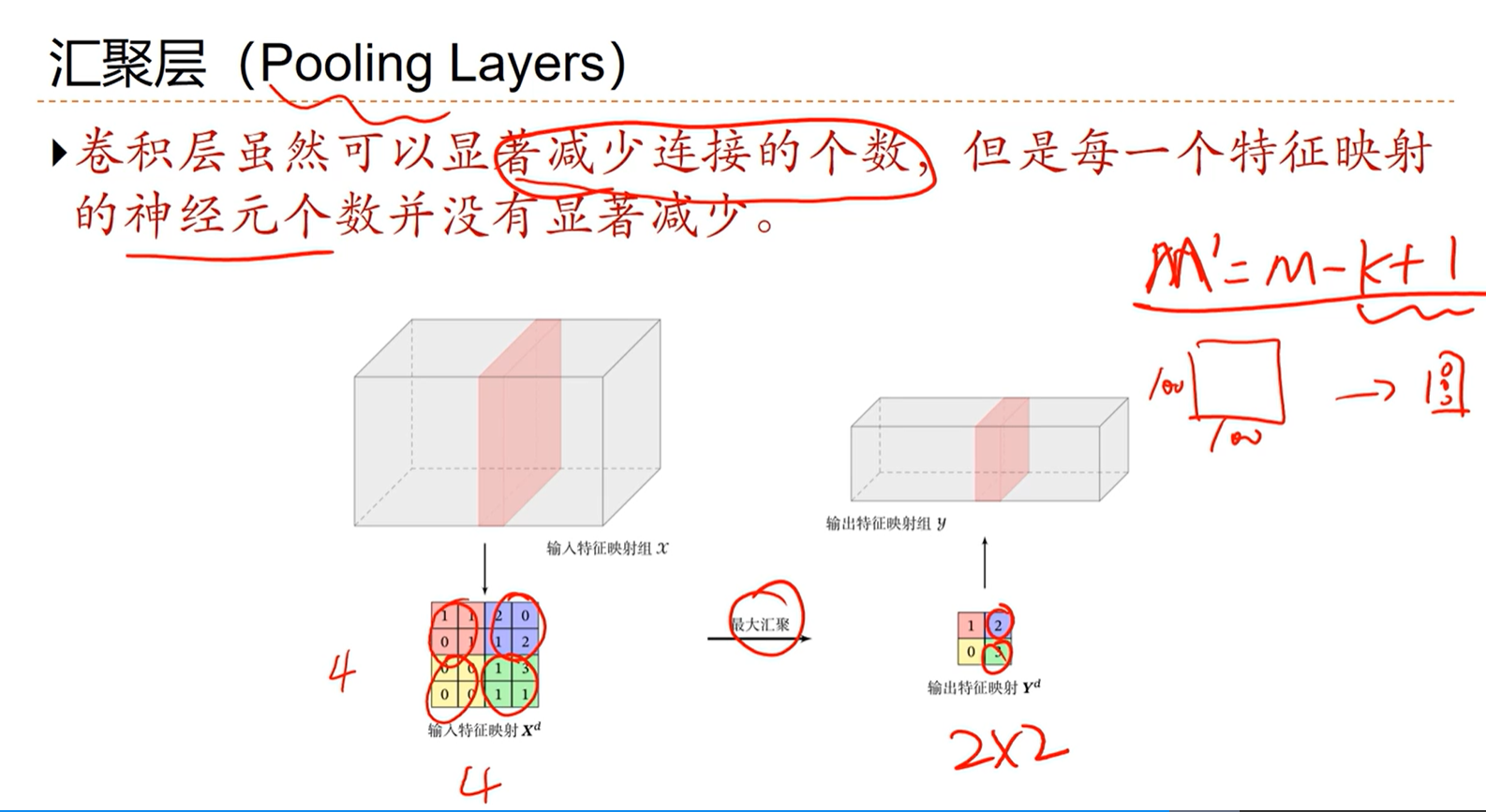
[√] 卷积网络结构
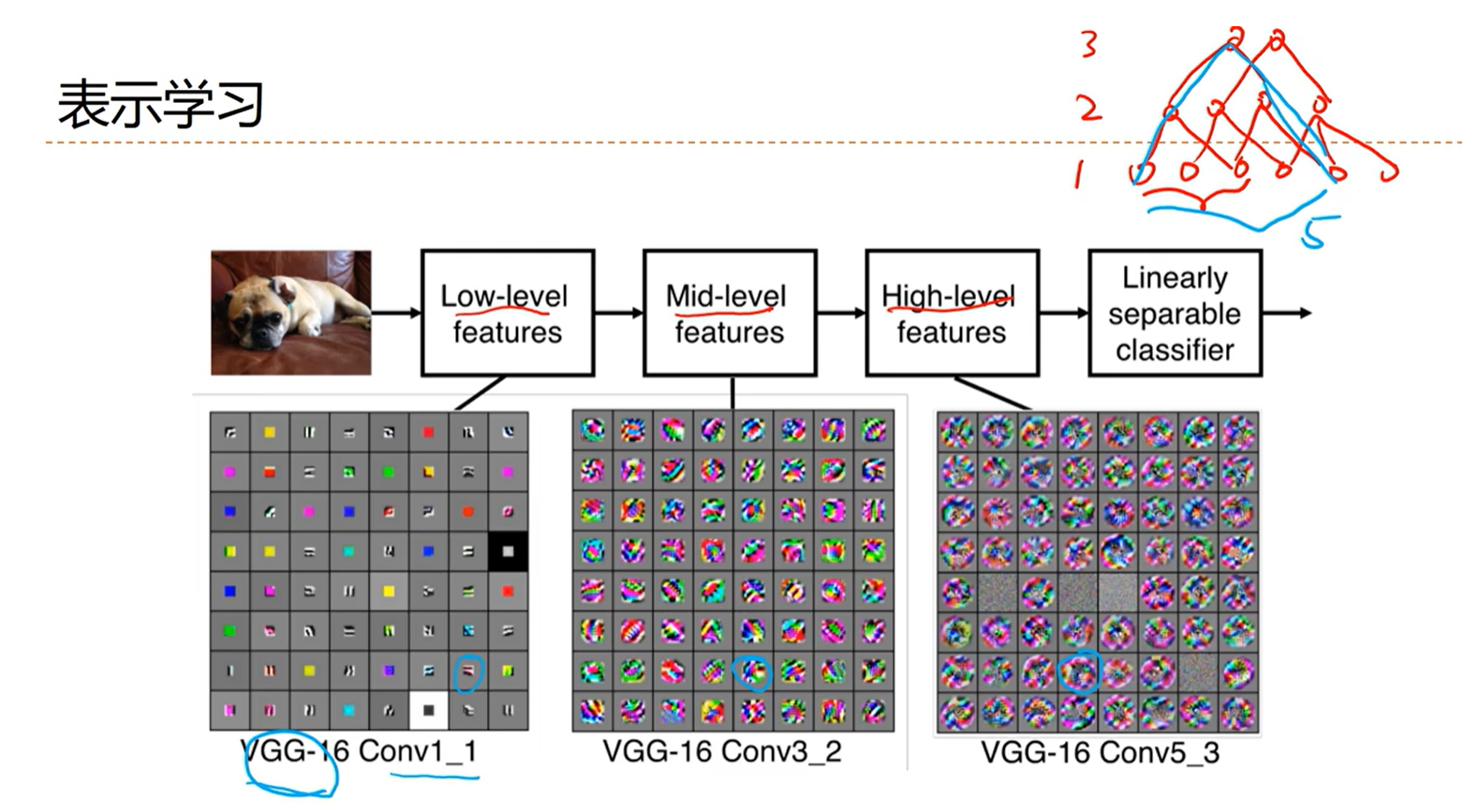
[√] 表示学习
alec:
卷积和表示学习是非常像的,用来学习特征。然后通过线性的分类器全连接网络进行特征的分类。
卷积的深层的神经元,视野更宽。
[√] 5.3 - 其它卷积种类
[√] 空洞卷积
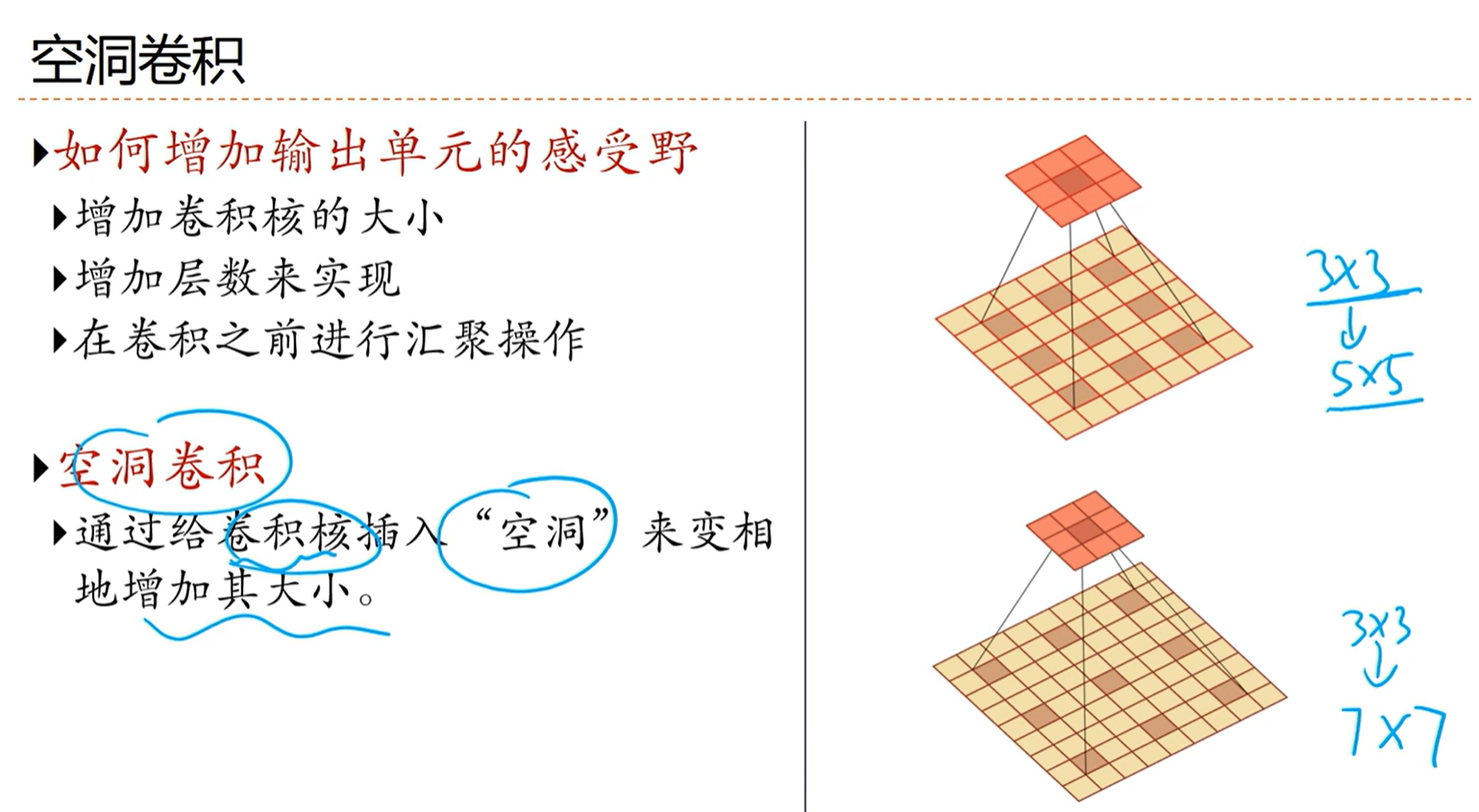
alec:
空洞卷积的作用是增加感受野
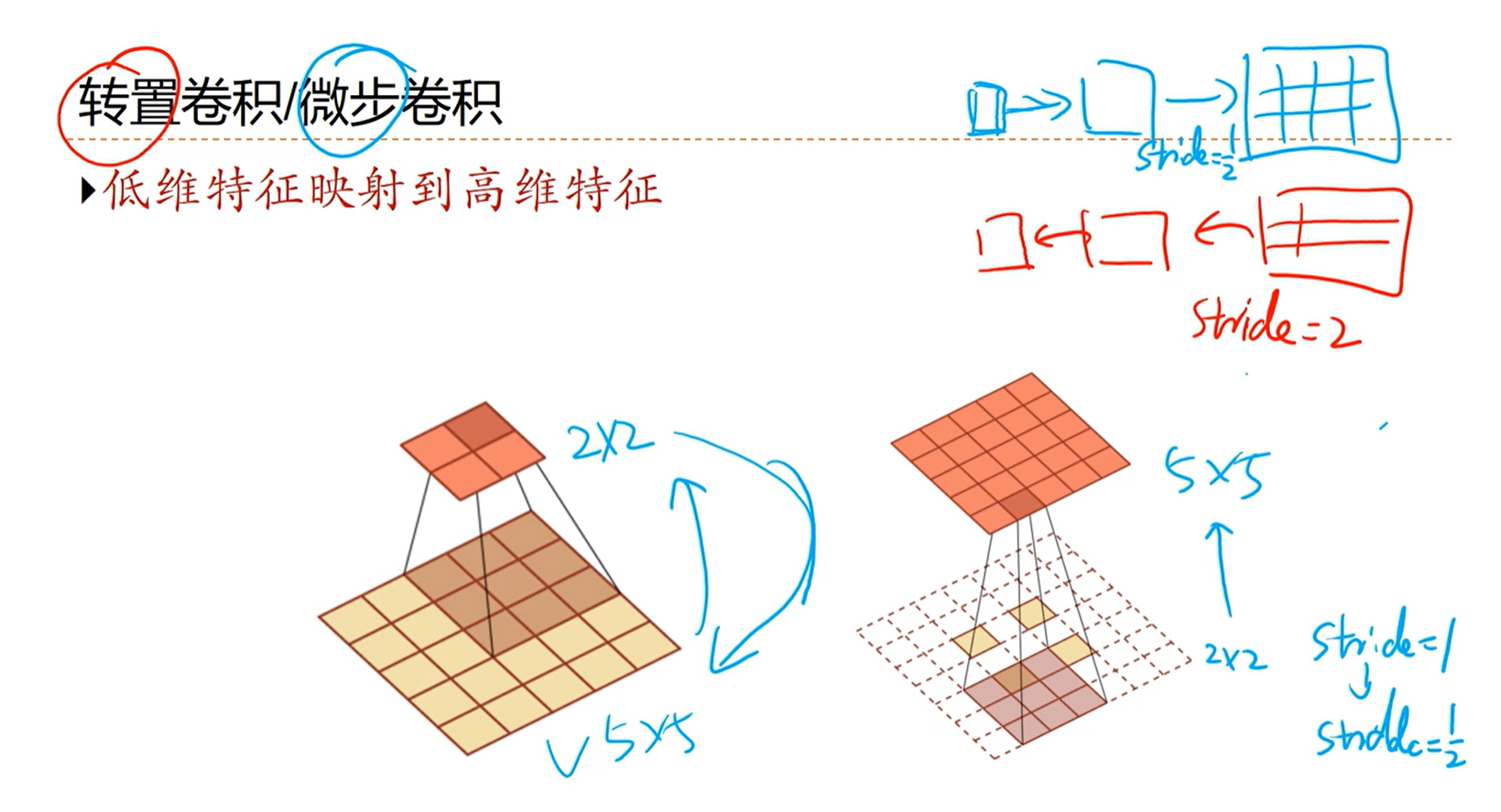
[√] 微步卷积/转置卷积
alec:
正常思路,随着卷积的进行,feature map会越来越小;当S>=1的是时候,输出会变小。因此当S≤1,输出就会变大。办法是对输入插0值,然后再卷积。
当想要输出比输入更大的时候,按照相反的思路来就可以,比如可以给输入进行补零,放大输入,然后再卷积,这样就能得到大的输出
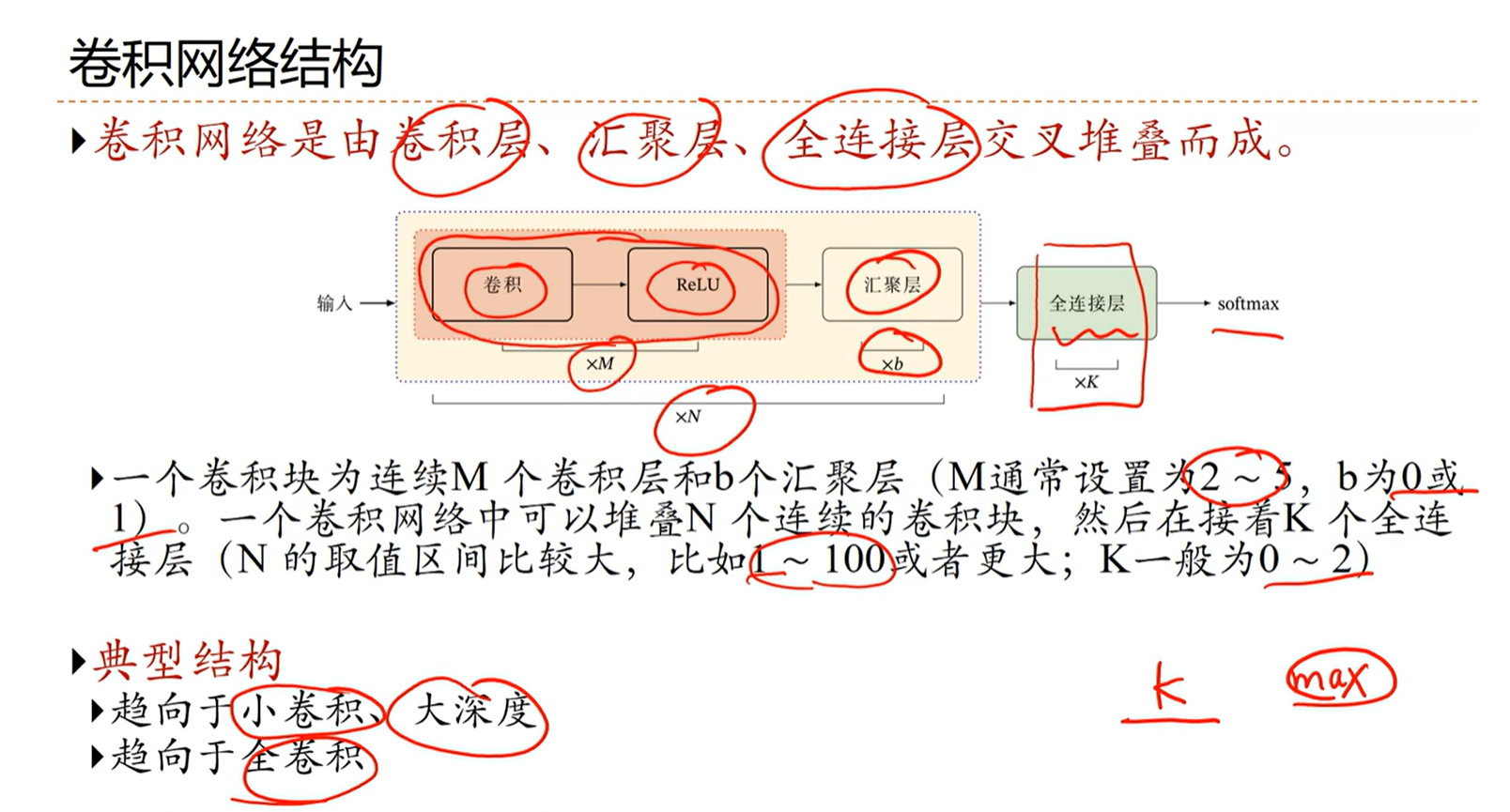
[√] 5.4 - 典型的卷积网络
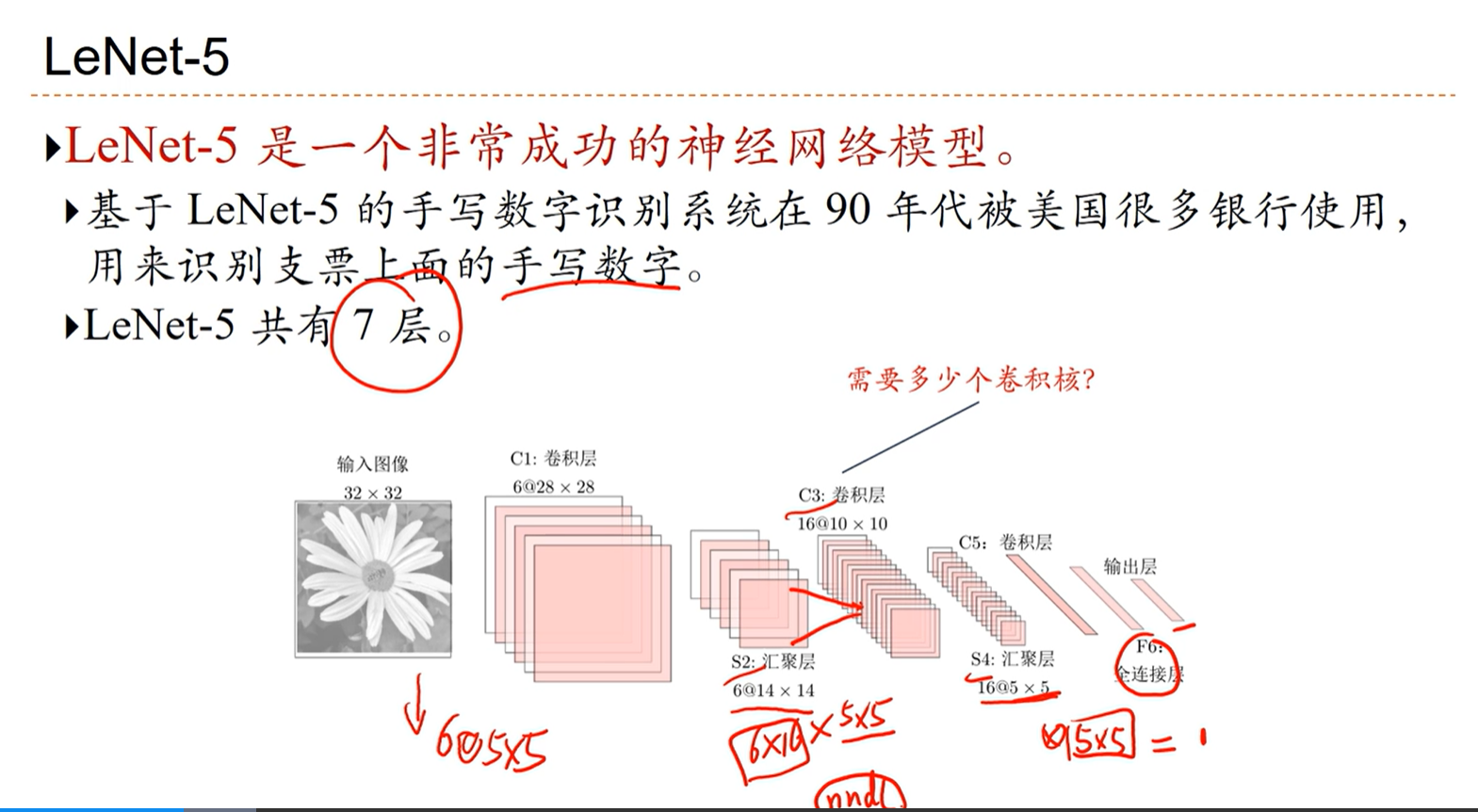
[√] LeNet-5
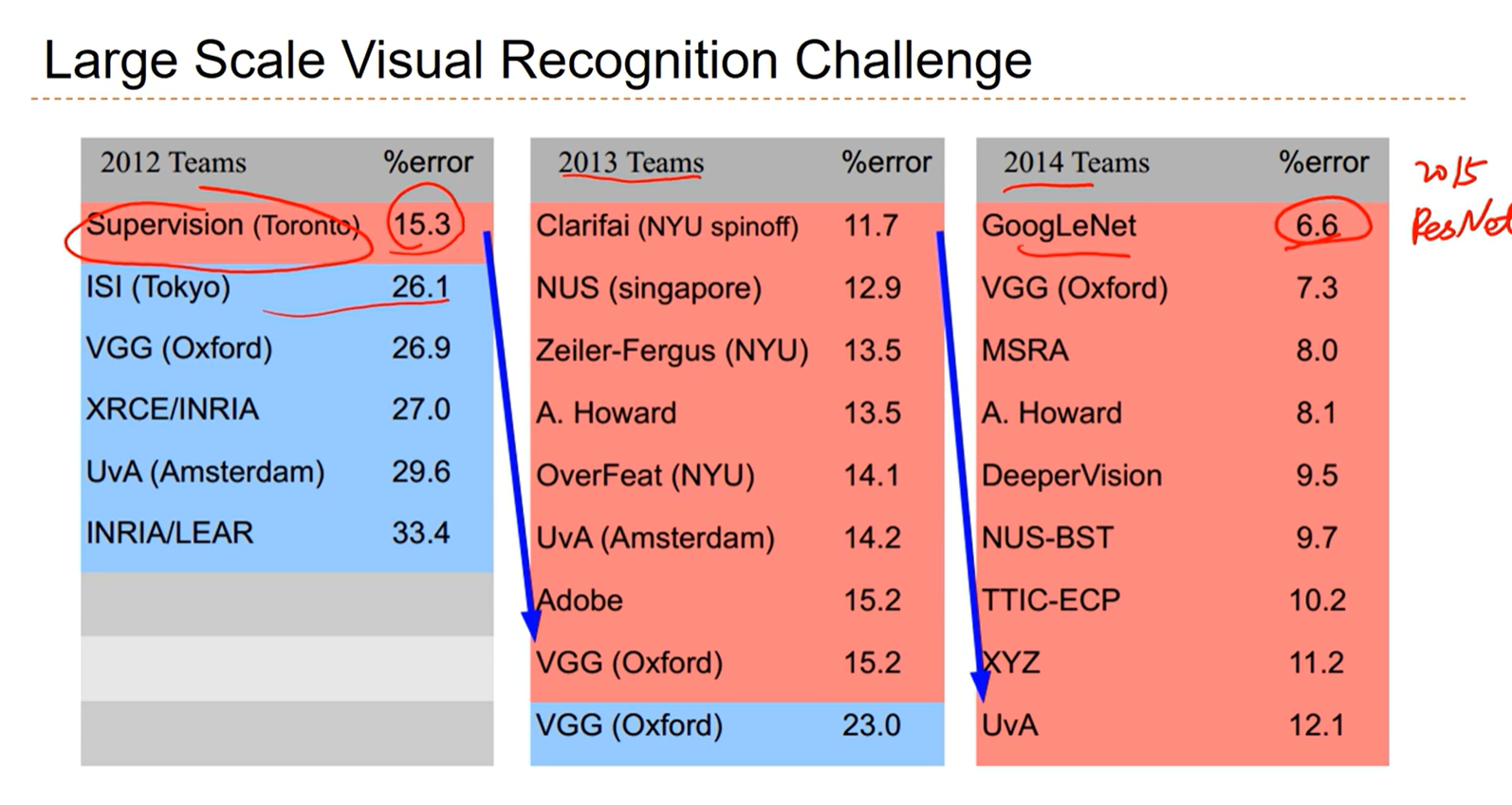
[√] 大规模视觉识别挑战
alec:
2015年何凯明提出的resnet在这个上面的准确率降到了3.几%,这个准确率已经超过了人的准确率。因此后面这个分类比赛就停办了。
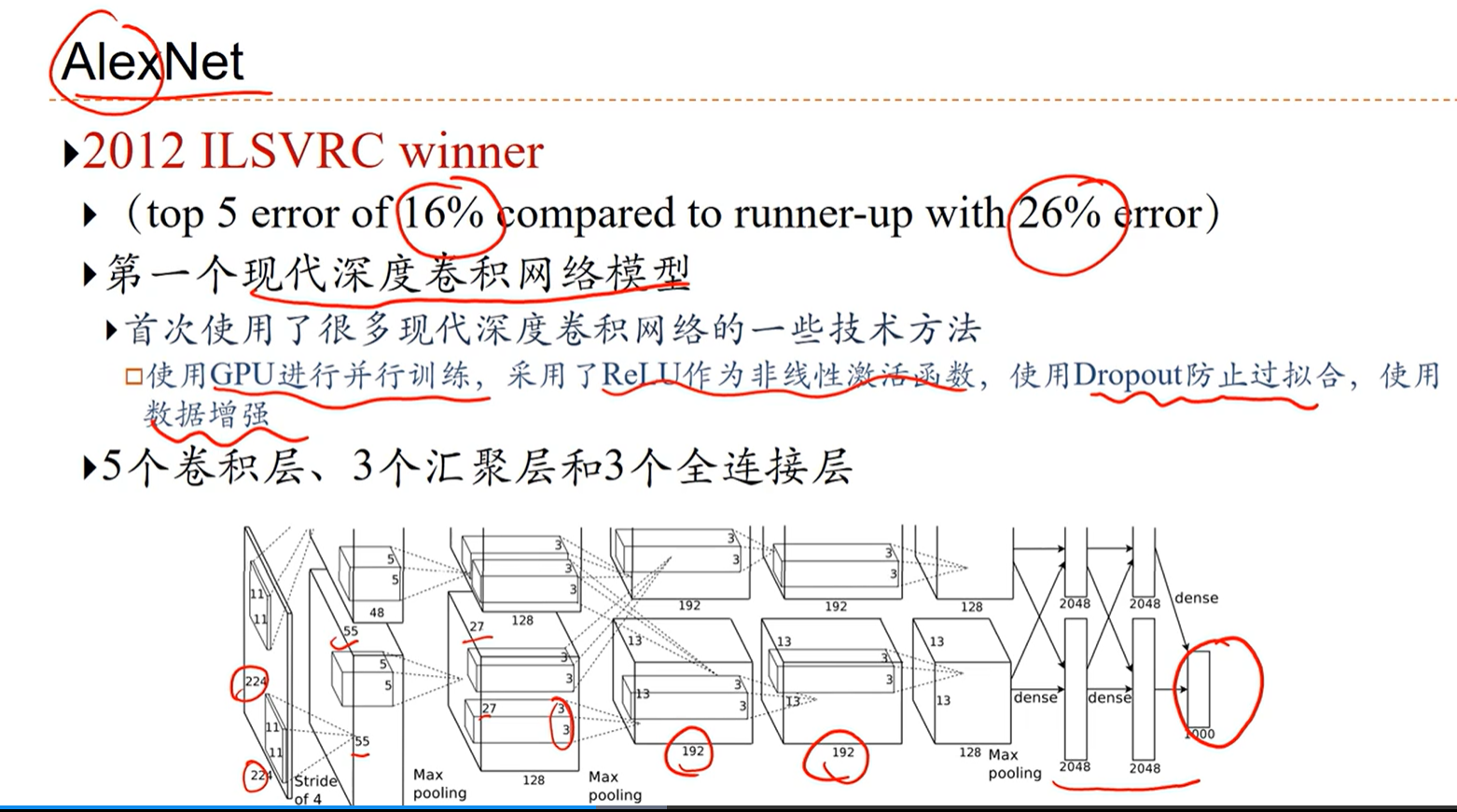
[√] AlexNet
alec:
卷积的起点就是AlexNet,Alex就是作者的名字
使用Dropout来防止过拟合
AlexNet是一个1000个分类的分类网络
[√] CNN可视化:滤波器

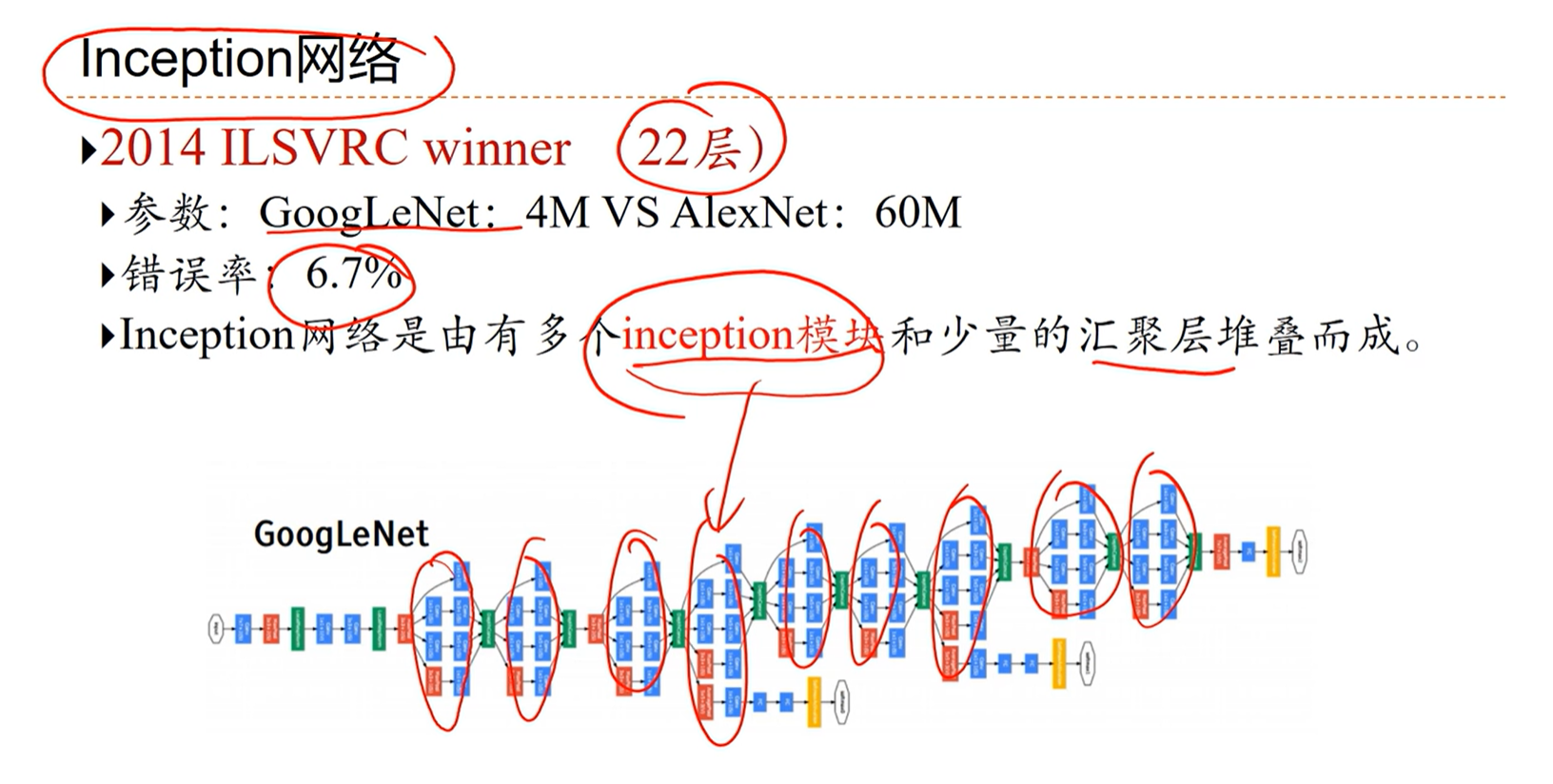
[√] Inception网络
alec:
Googlenet是属于inception网络的第一版
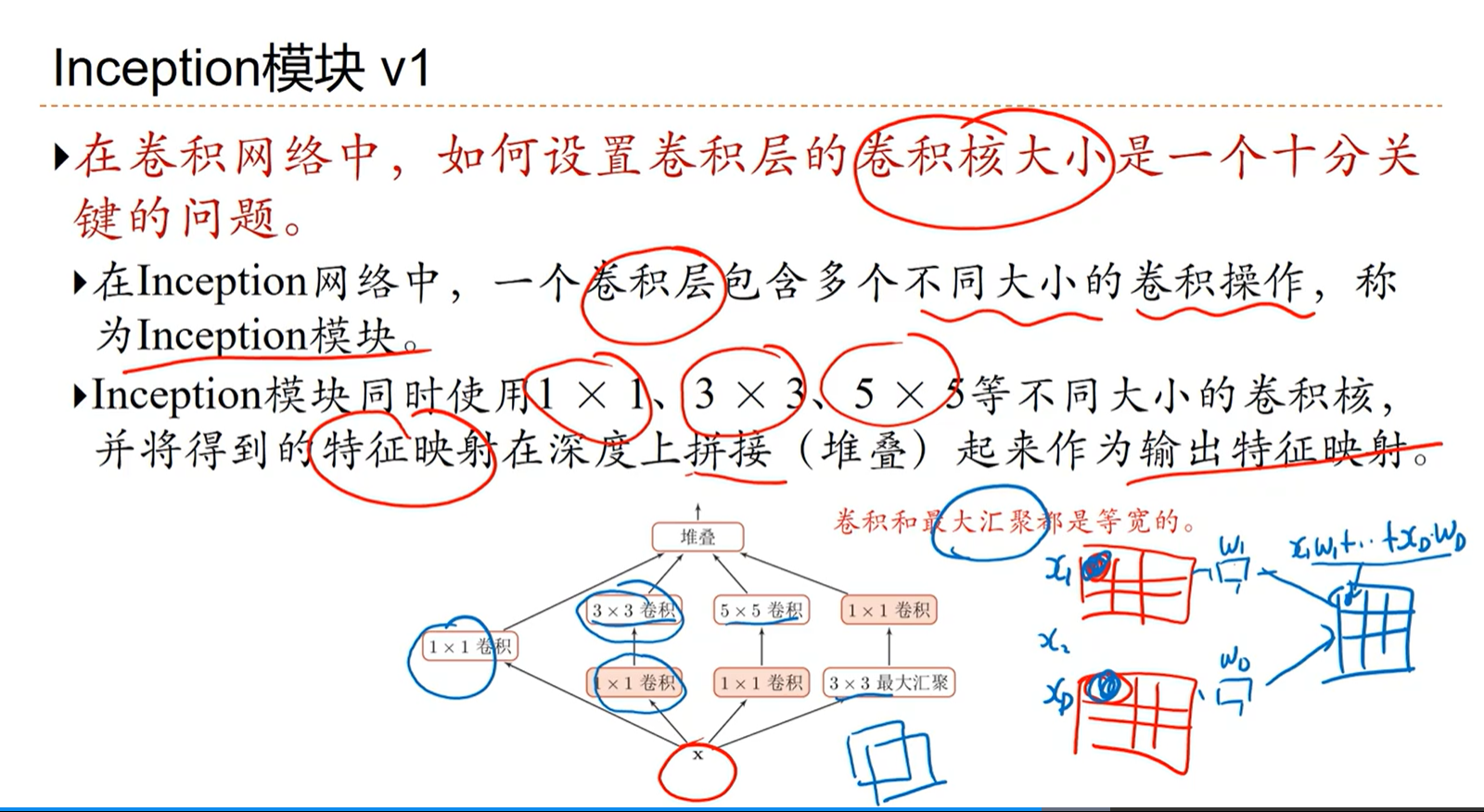
[√] Inception模块V1
alec:
- 在卷积中,卷积核选择多大的尺寸是一个非常难的问题。因此在Inception中,在同一层卷积中,选择多个不同大小的卷积核放在同一层,这种模块成为Inception模块。
- 同一层中不同尺寸的卷积核,卷积(等宽卷积)和最大汇聚后的特征图都是等宽的,因此在同一层之后,可以将特征图汇聚堆叠到一起,然后传给下一层。
- 穷举各种大小的卷积核,极大的提高了特征的丰富程度。因此网络的能力会变得更强。
- 1×1卷积其实就是在深度(通道数)这个方向对元素做了加权组合。看成是不同通道上的特征融合。1×1卷积不改变大小,因此不需要padding
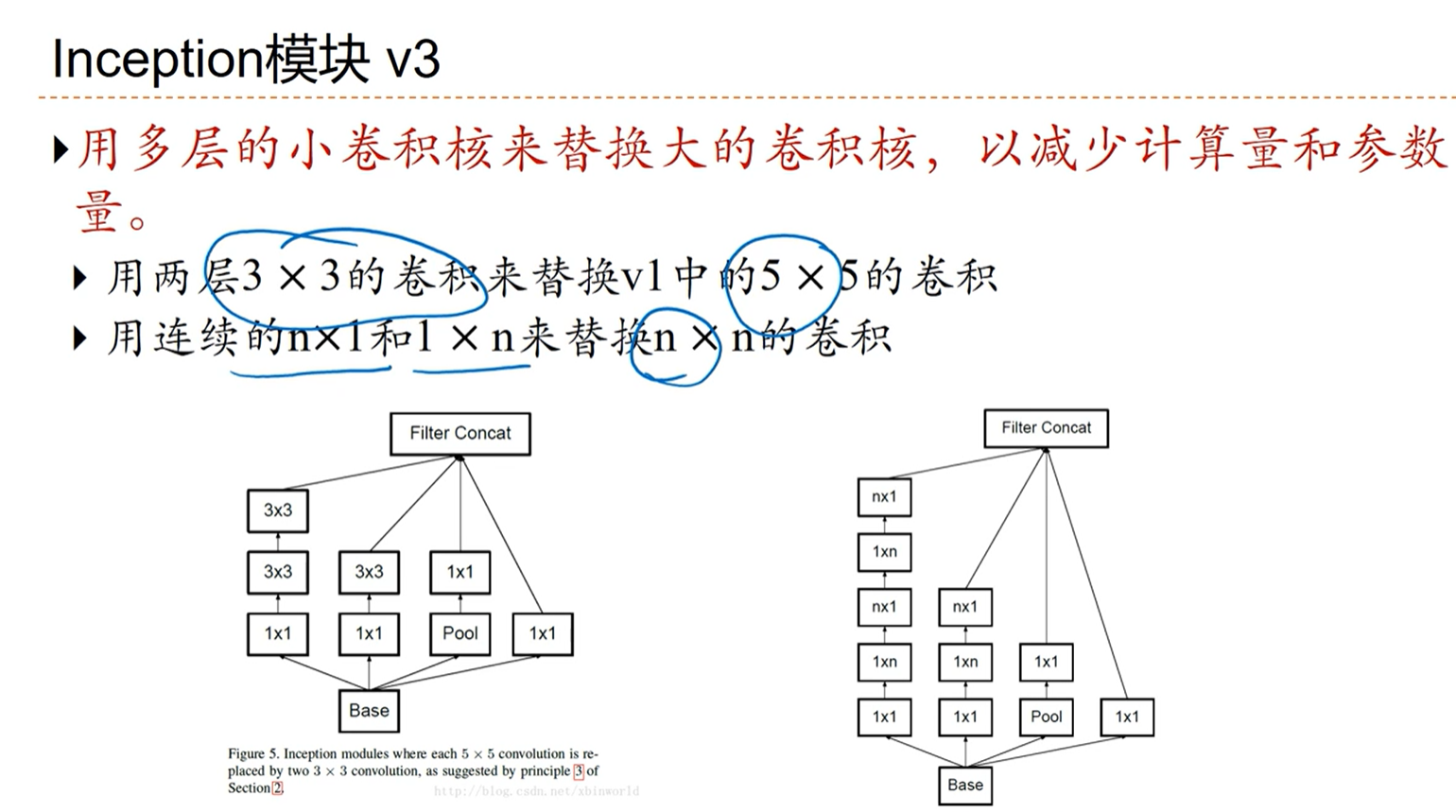
[√] Inception模块V3
alec:
3×3的感受野小于5×5的感受野,但是3×3串联3×3,那么感受野就变大了。因此通过串联小卷积核替代大卷积核,这样可以减少参数量。
[√] 残差网络
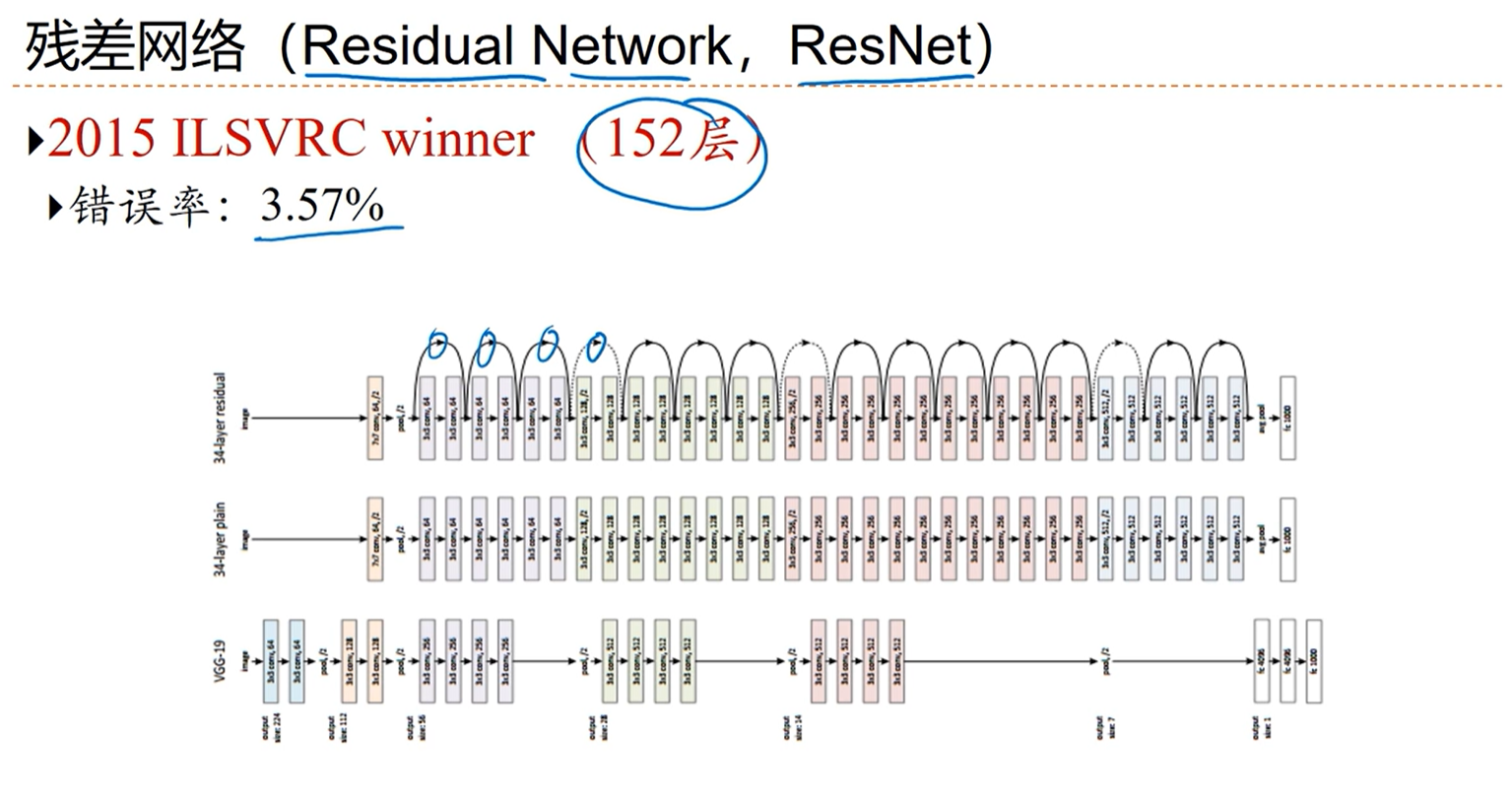
alec:
当f(x)是一个恒等函数的时候,反而用卷积神经网络模拟非线性的函数很难逼近这个函数。因此通过残差网络直连边的方式,能够优化这个问题。
h(x)= x + f(x), x是线性部分,f(x)是非线性部分
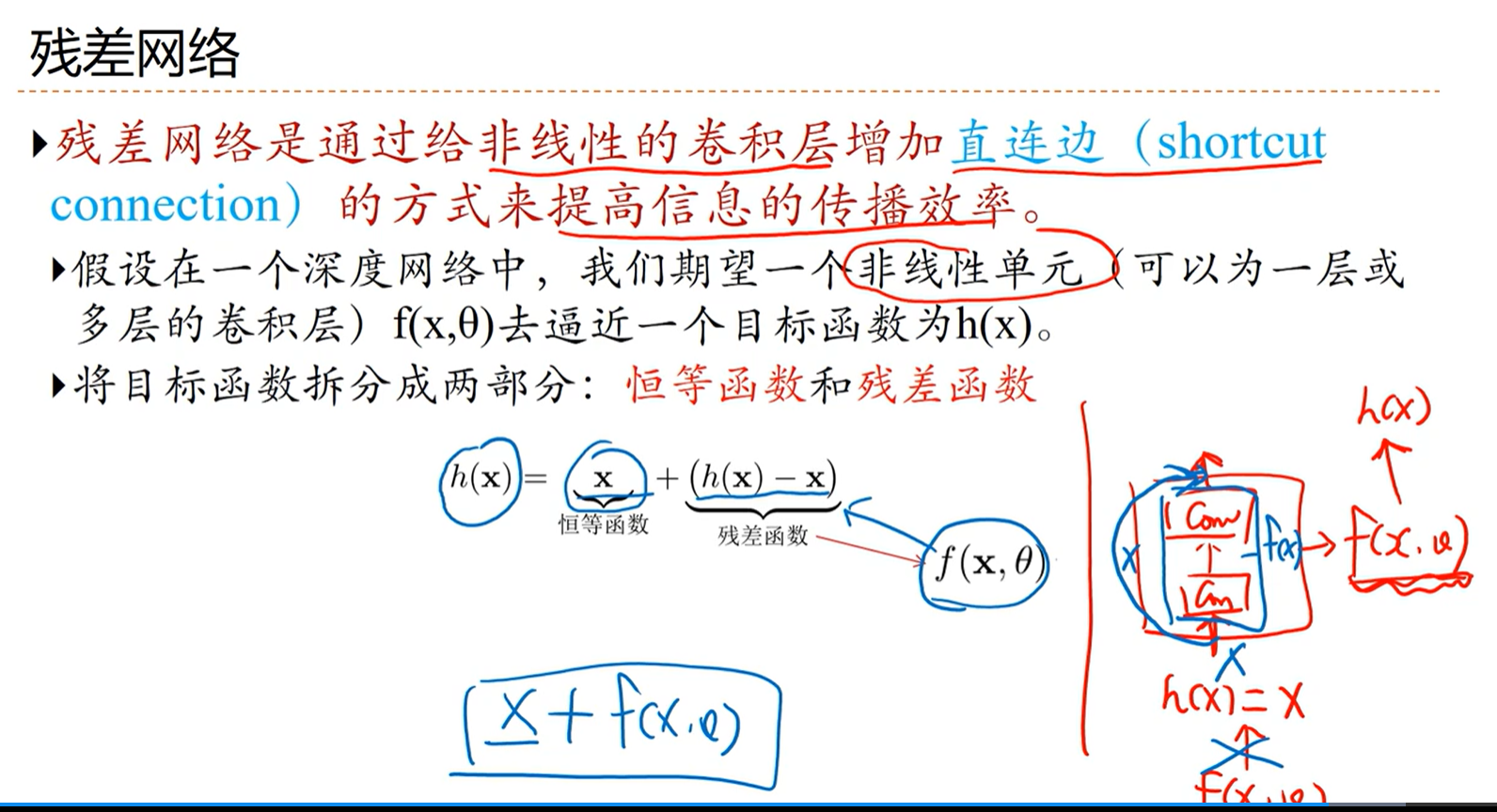
[√] 残差单元
alec:
- 残差单元,等宽卷积边和直连边相加之后,再激活
- 一个block中的卷积怎么搭配,是一个非常灵活的事情
为什么残差网络能够深度非常深?
- 深层网络存在的一个问题是层数太深、梯度消失问题。残差网络的导数为(x+f(x))‘ = 1 + f‘(x)
- 因为这个1的存在,所以梯度不会变的很小,所以能够缓解梯度消失问题
- 因此,现在对于任意一个比较深的网络,即使不是残差网络,这种残差直连边的连接方式,已经成为了一种必不可少的技术
[√] 5.5 - 卷积网络的应用
[√] AlphaGo
alec:
强化学习中决策网络,下棋相当于在19×19的棋盘中,确定棋盘中下棋的位置,相当于一个输入是一张图像,输出是一个19×19的分类问题。
强化学习中的价值网络,用来判断走每一步对于后面的平均收益是多少。
这两种网络都是通过卷积网络来实现的。
等宽卷积:
- 填充 P = (K - 1)/2
等宽卷积的目的是为了适应残差网络中残差边和直连边的相加
残差网络的目的是为了优化梯度消失问题

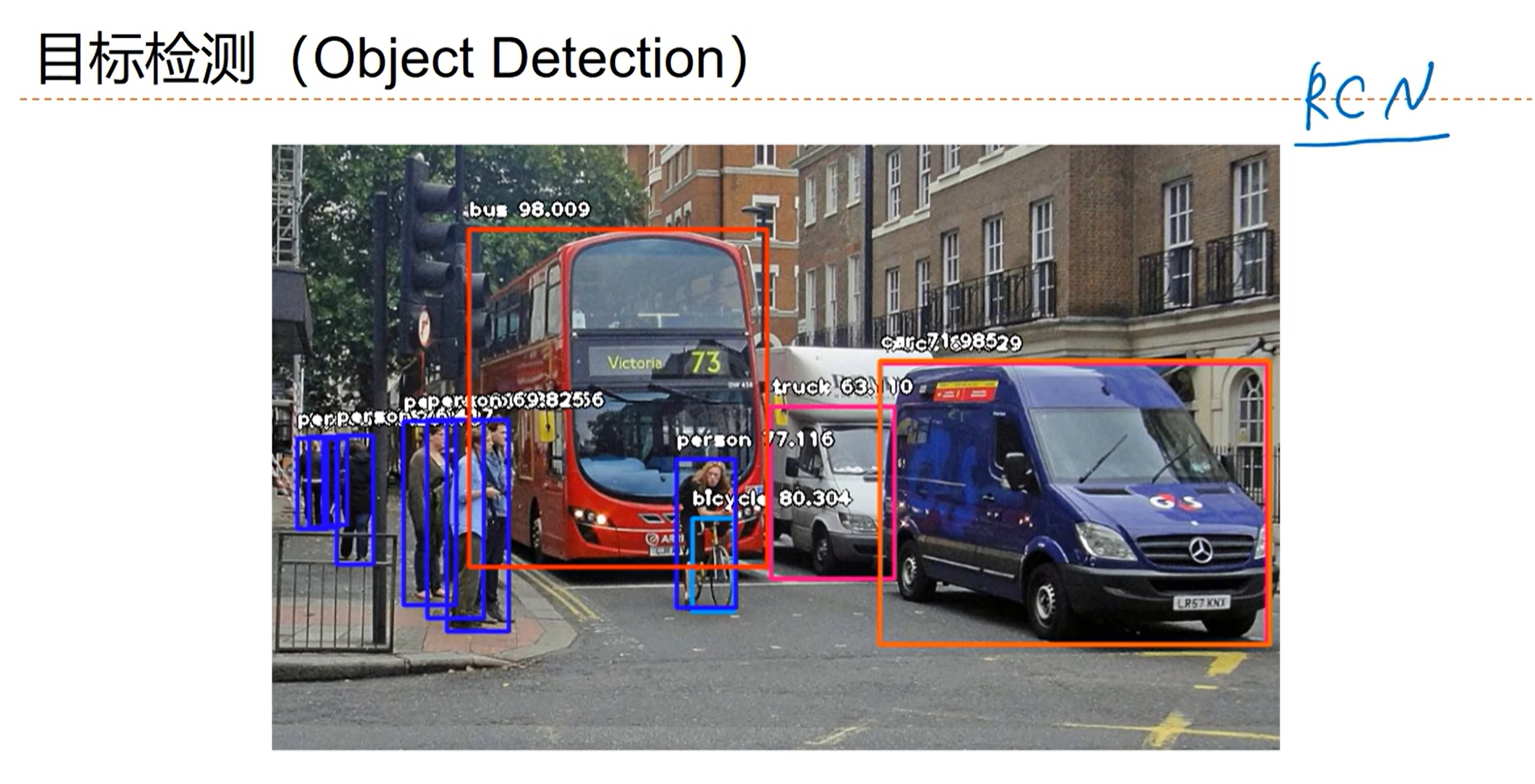
[√] 目标检测(Object Detection)
alec:
目标检测中有自己专门的卷积网络:RCN、区域卷积网络
[√] Mask RCNN
alec:
更细粒度的,像素级的图像分割,将轮廓找出来。
思想类似于讲图像中的某个区域拿出来,然后做像素级别的分类,从而找到目标轮廓。

[√] OCR

[√] 5.6 - 卷积网络应用到文本数据
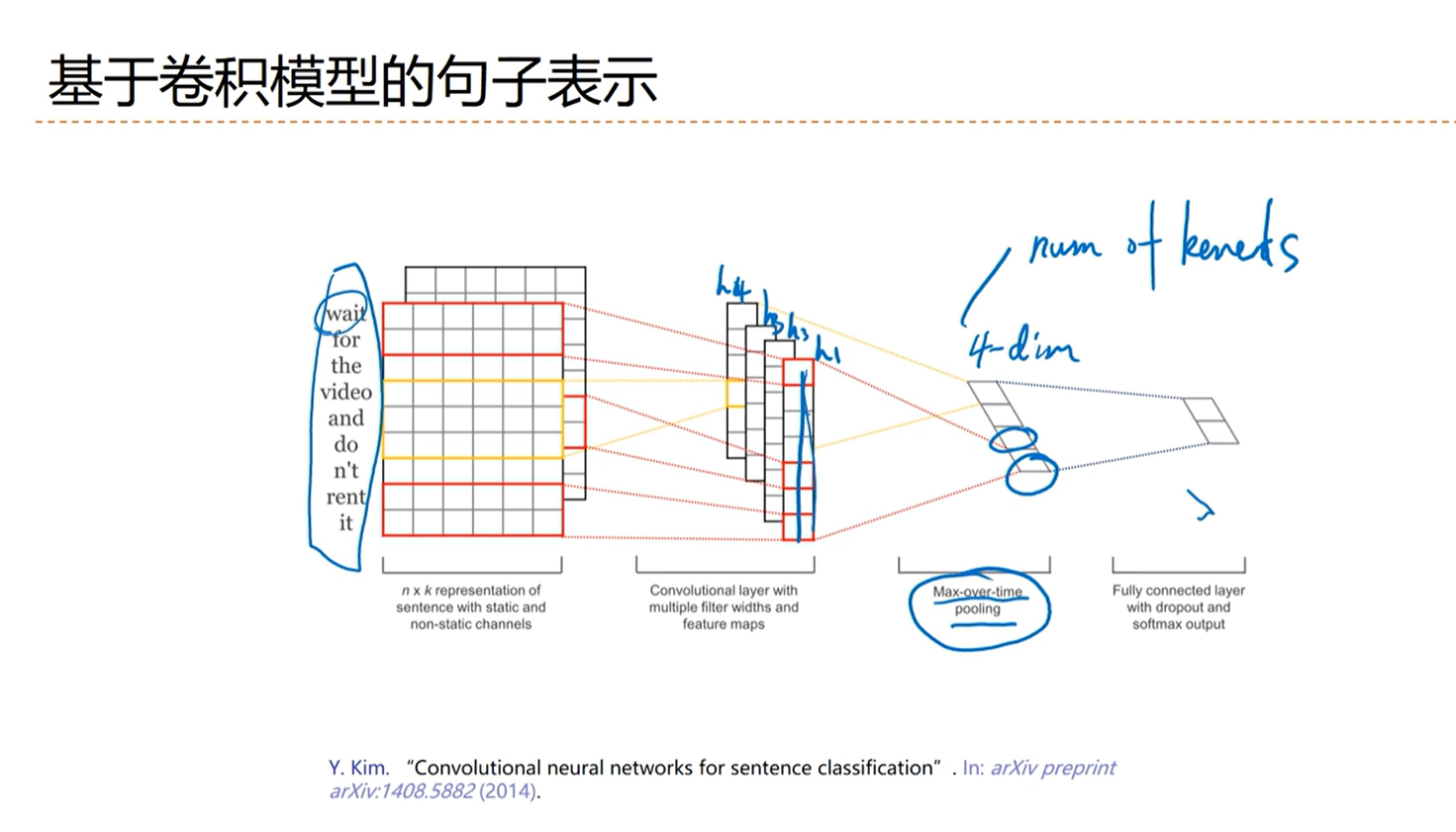
[√] Ngram特征与卷积
alec:
卷积是从信号序列提取特征,文本本身就是信号序列,因此使用卷积提取文本信息是自然的
单个词语的提取,会丢失数据的顺序(unigrams)
因此可以两个、三个词语的提取(bigrams、trigrams)
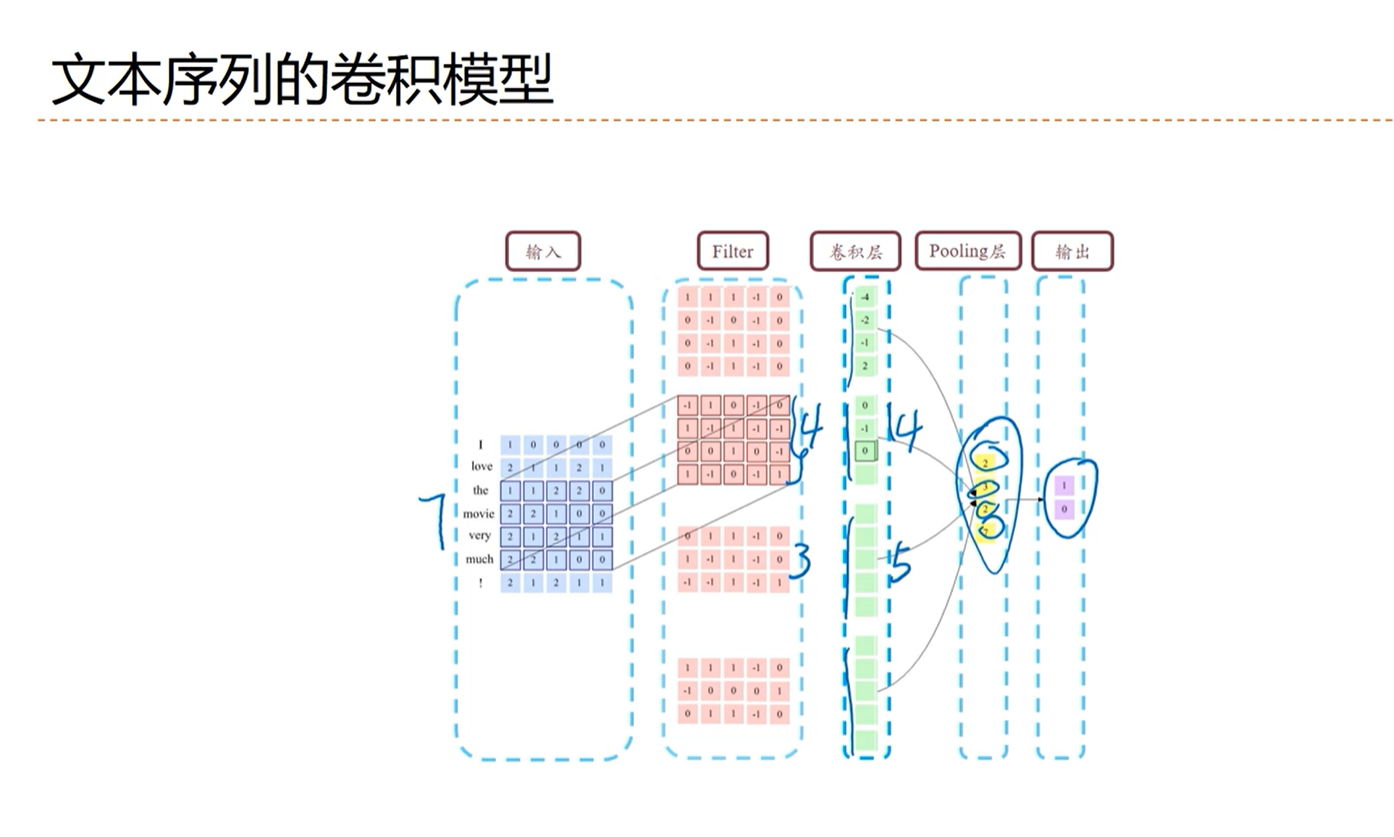
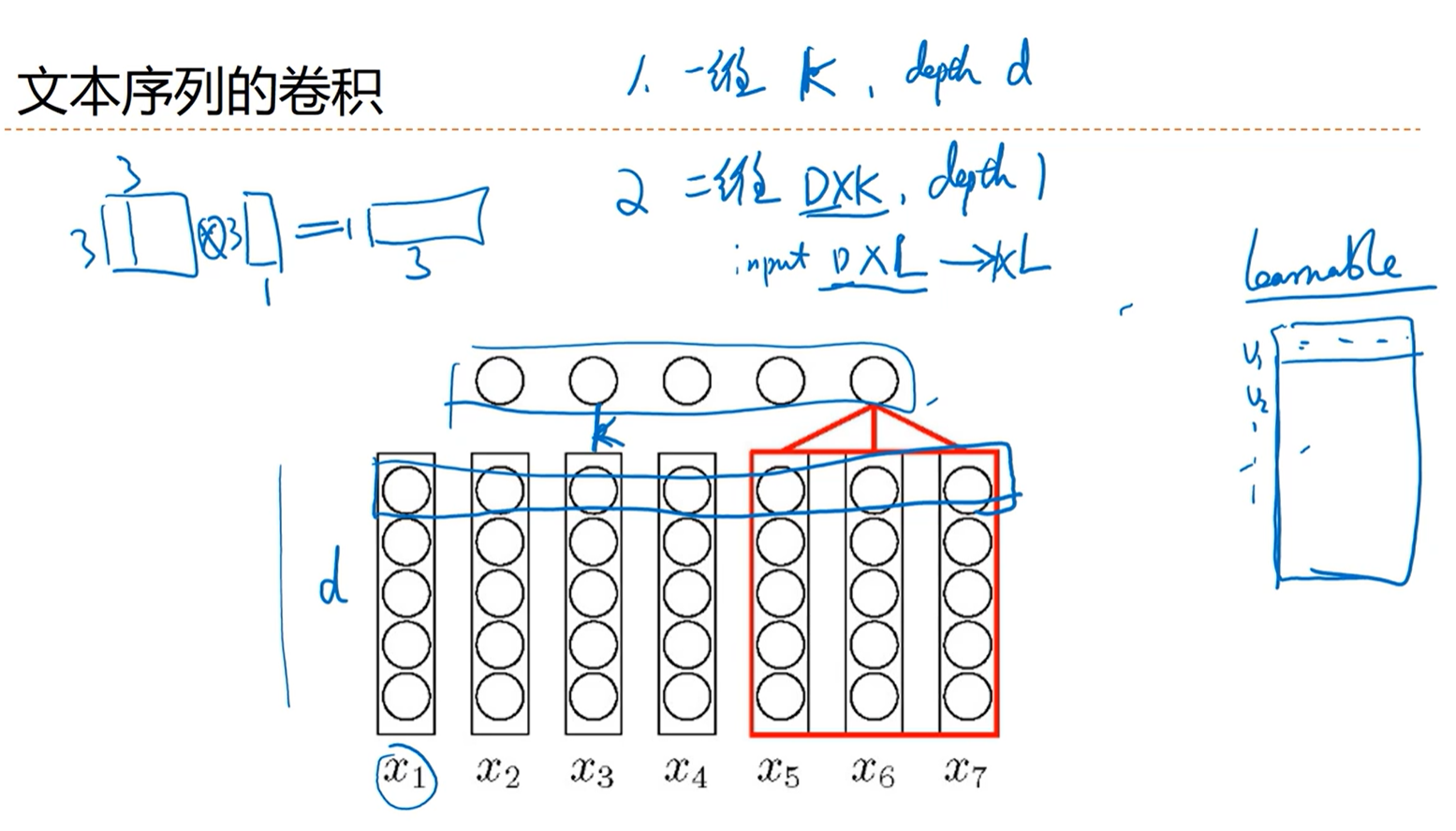
[√] 文本序列的卷积
[√] 基于卷积模型的句子表示
[√] 文本序列的卷积模型
alec:
卷积层是指的使用卷积核卷积前一层数据之后,得到的新的特征图,这些特征图是通过卷积得到的,所以叫卷积层;这一层是卷积的结果,而不是说这一层是进行卷积的过程。