第1章 - 实践基础1

本文最后更新于：3 个月前

[√] 课节1: 实践基础

1.1 - [视频] 直播回放——邱锡鹏老师

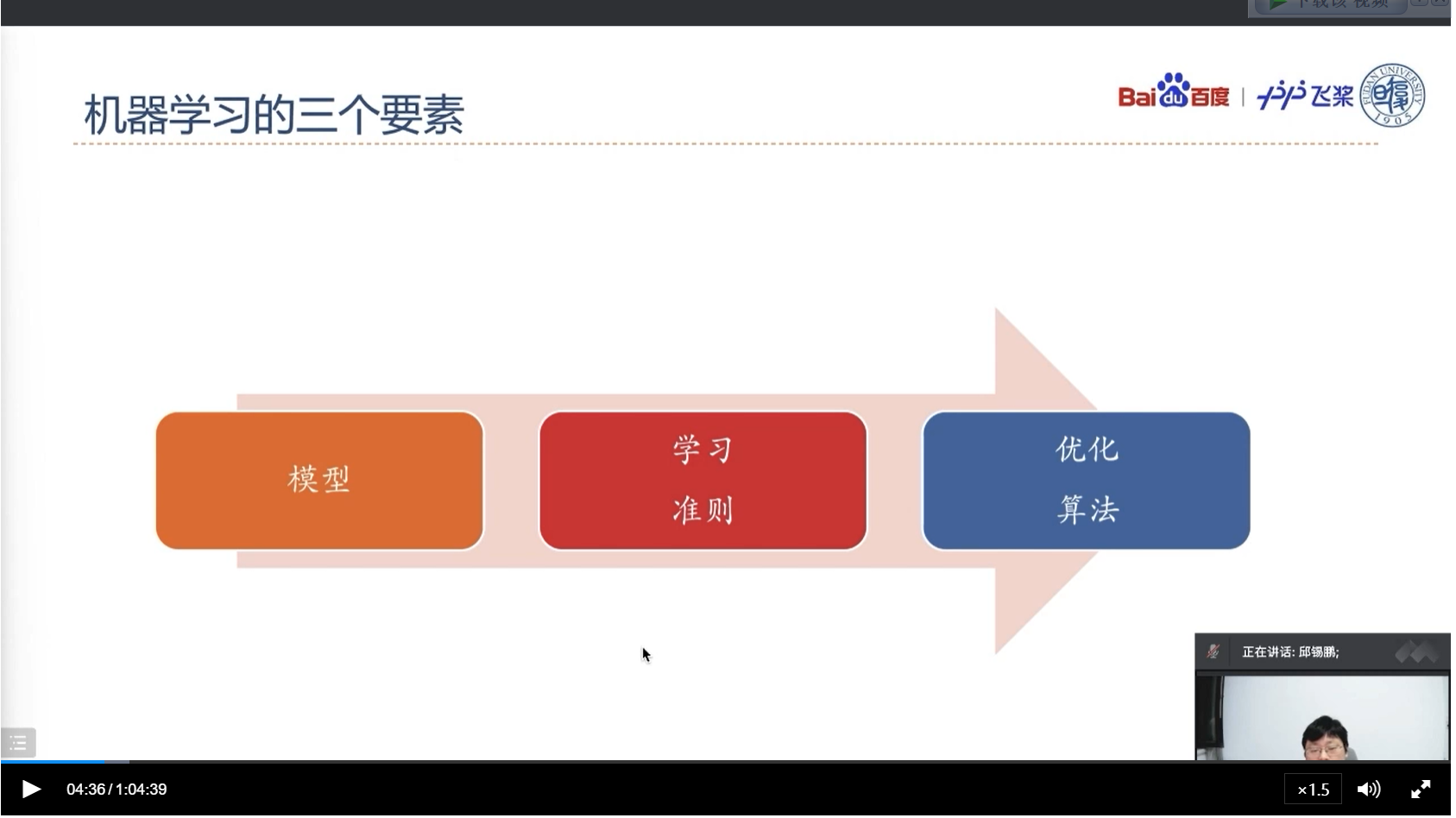
image-20221209164905028

image-20221209164937541

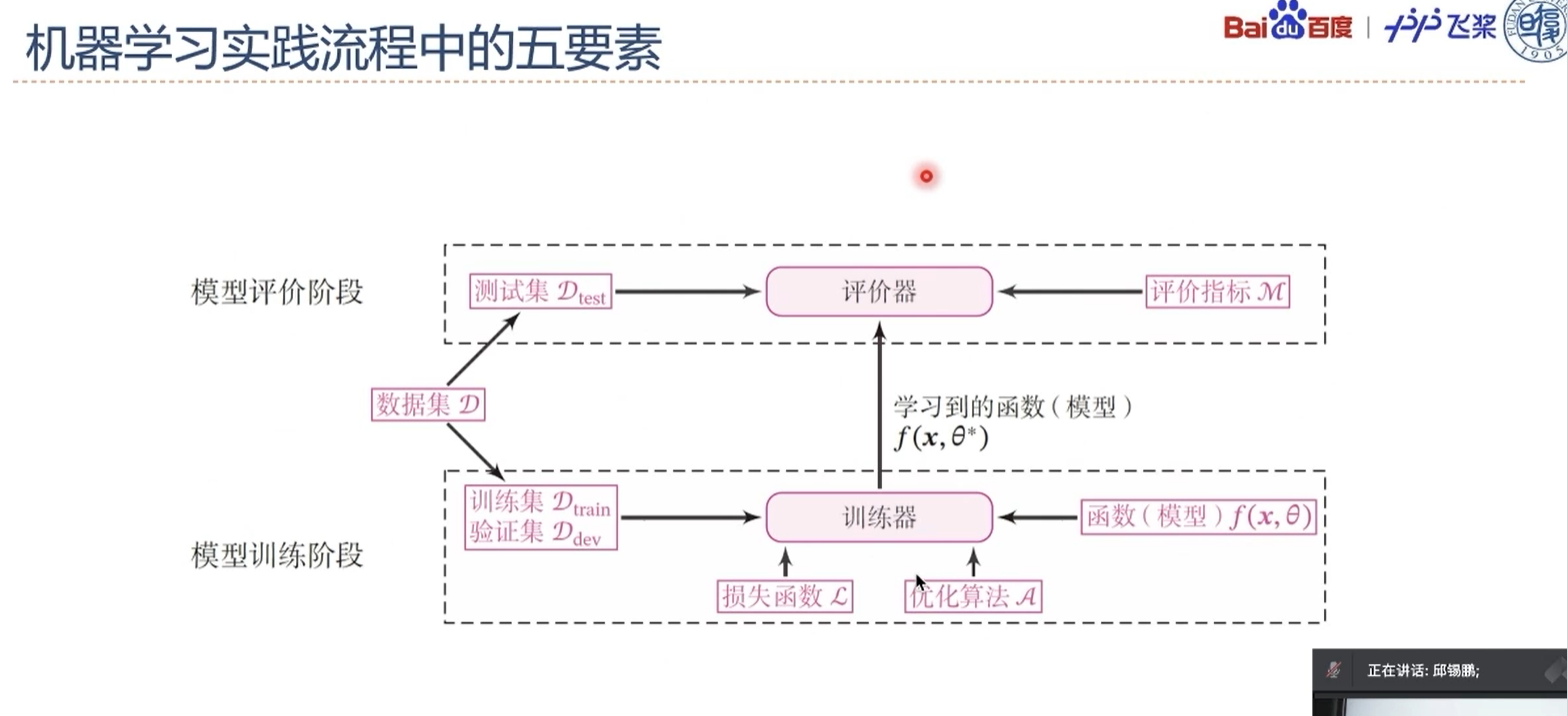
模型需要自己构建，其中线性模型可以看做浅层学习，非线性函数可以看成深层学习或深度学习

学习准则可以定义为一些损失函数来评判学习的好坏

有了学习准则之后可以通过一些优化算法来优化，让其在学习准则下达到最优

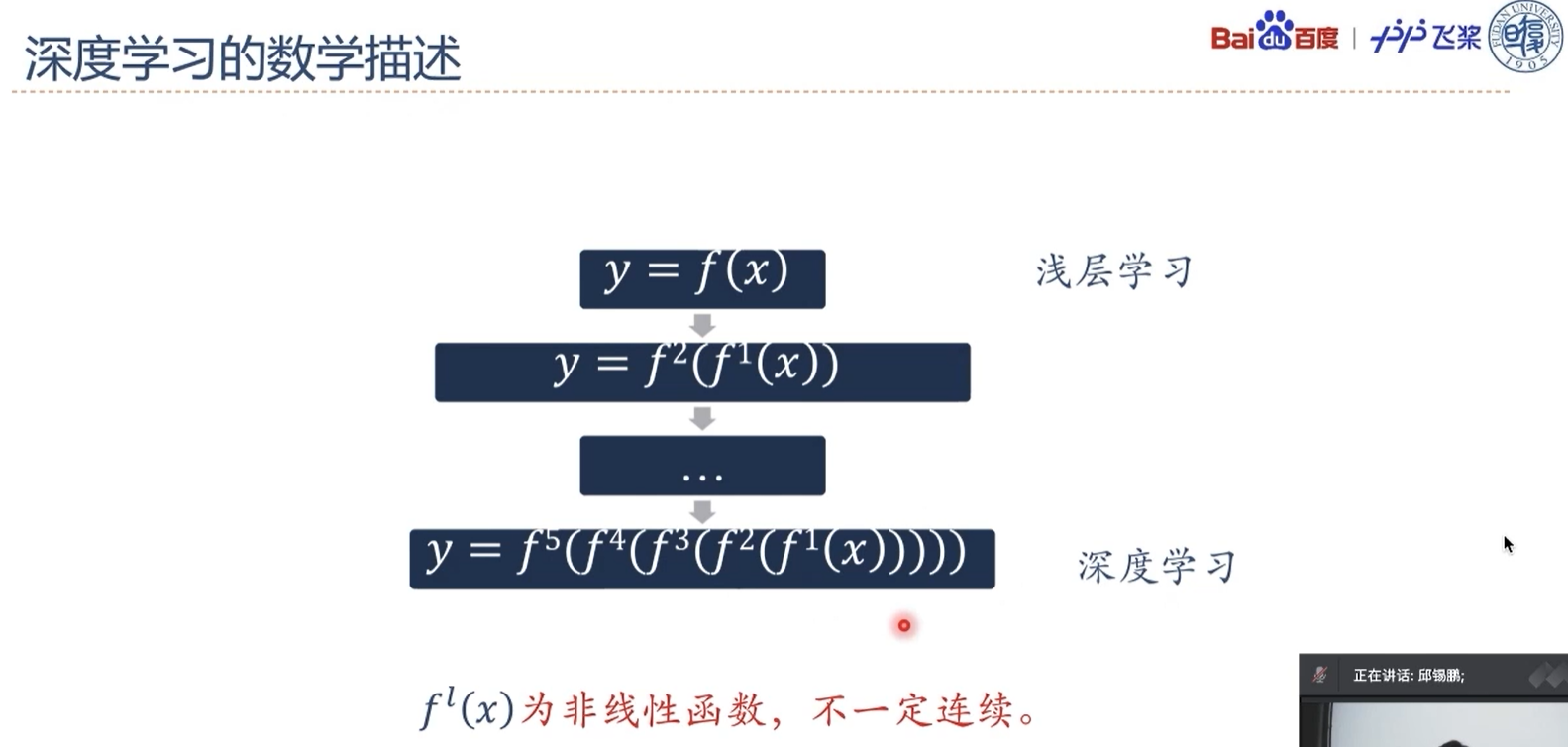
image-20221209165332527

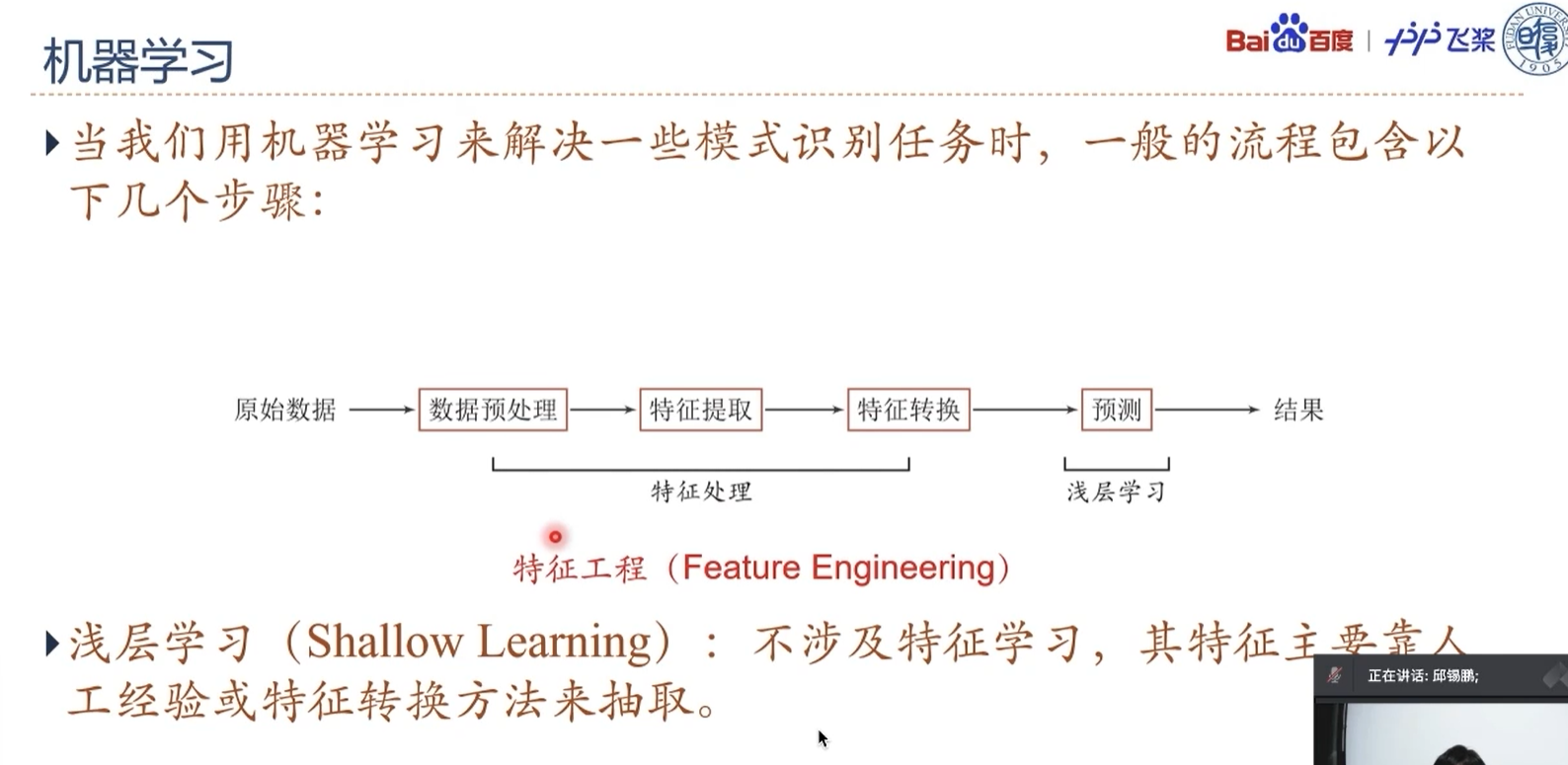
image-20221209165554684

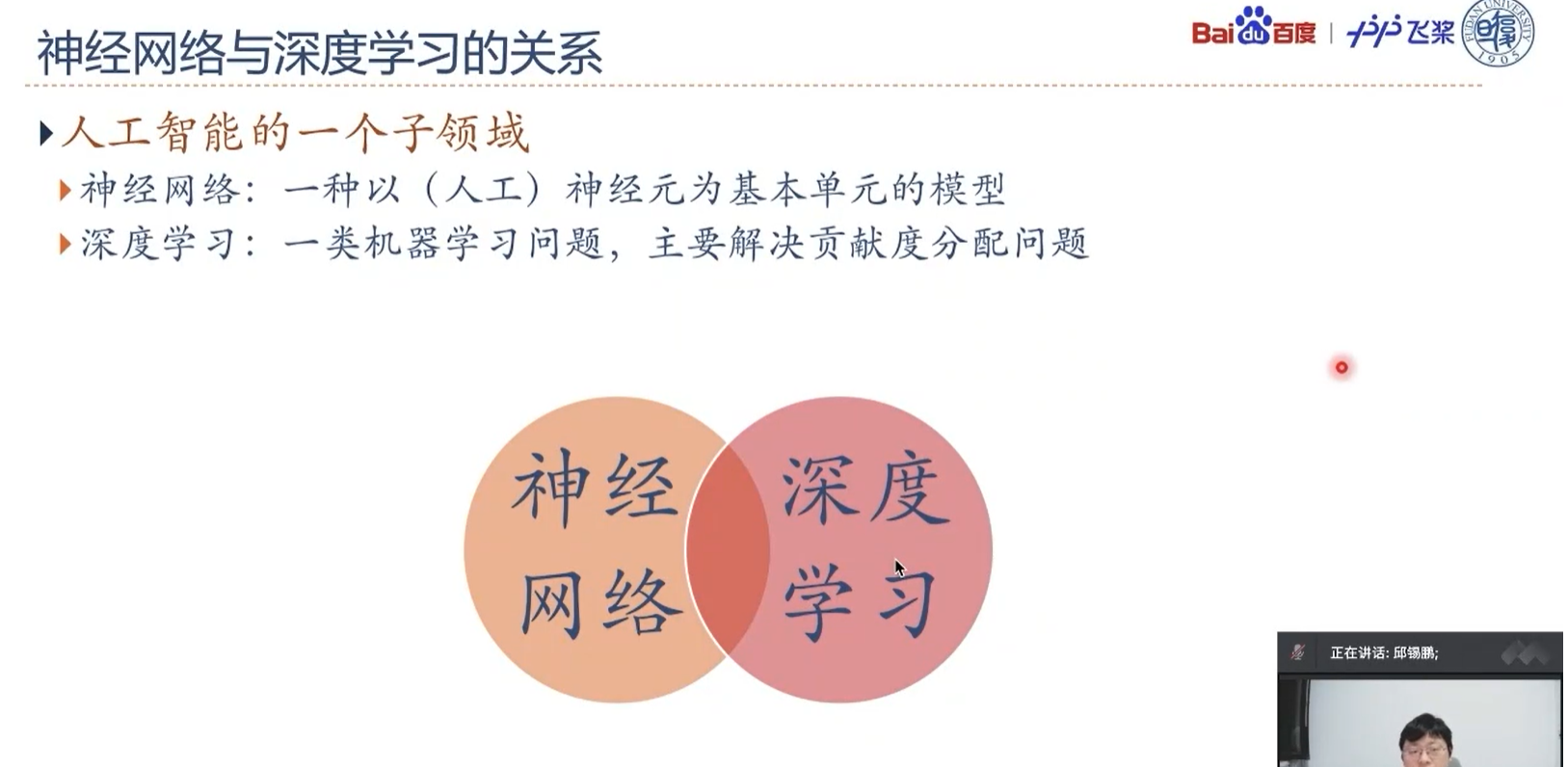
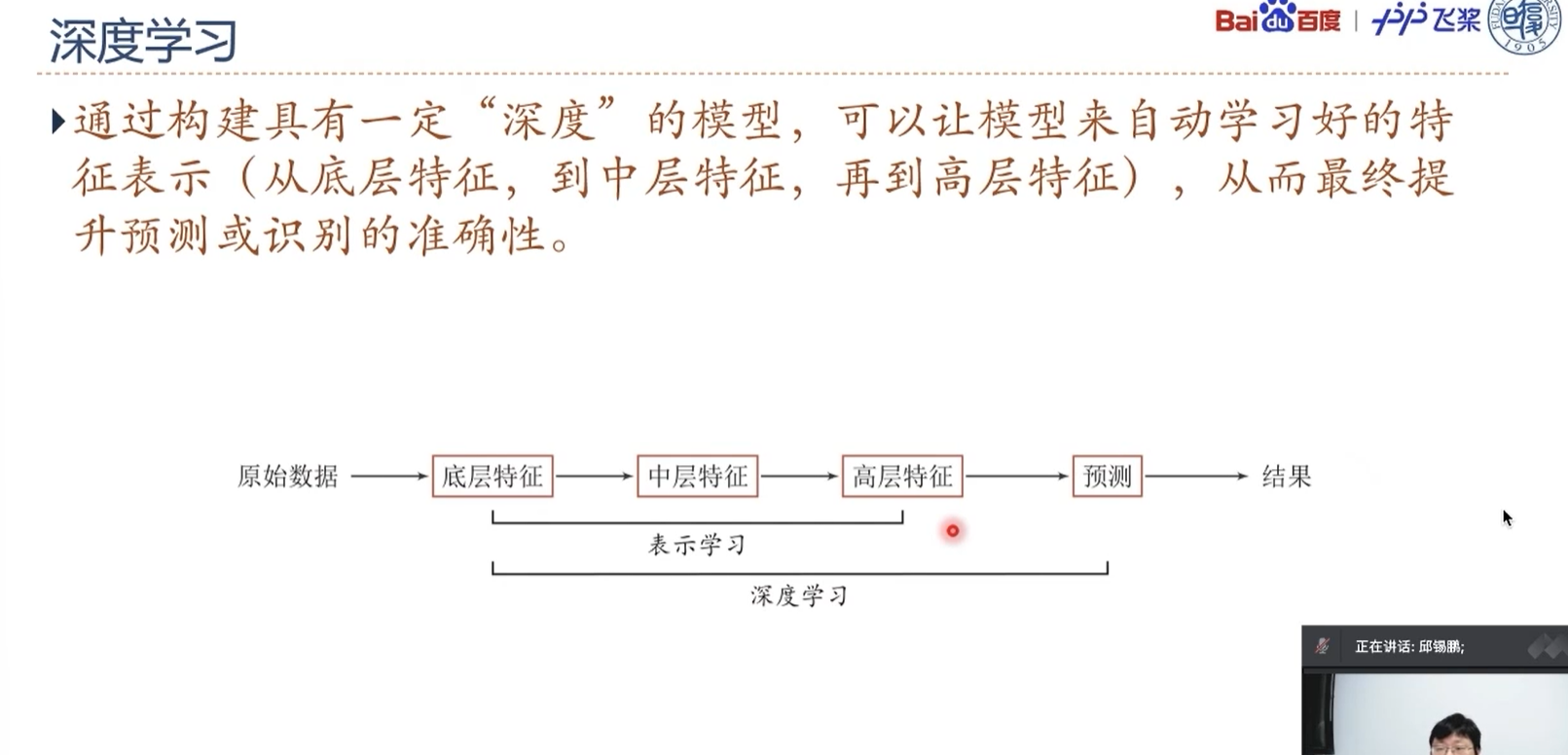
深度学习 = 表示学习 + 预测

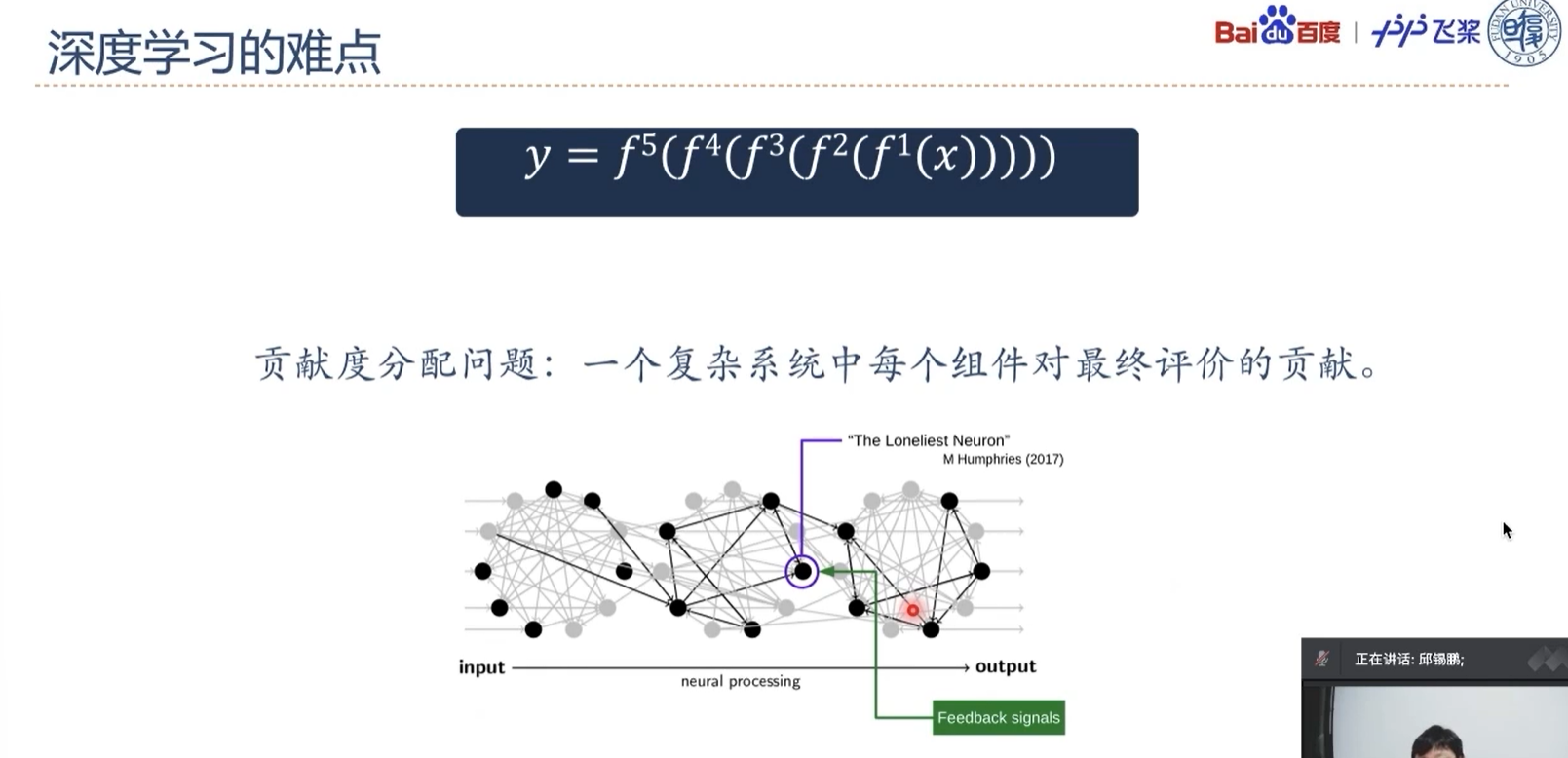
image-20221209165732312

image-20221209165820537

image-20221209170102382

通过偏导数，在机器学习中，对参数稍微调整一下，看一下这个调整对最终结果的影响是多少，从而确定这个参数是否重要已经应该怎样调整这个参数。

image-20221209170339498

深度学习是一类机器学习问题，主要解决贡献度分配问题，此处的贡献度分配就是指的神经网络模型中的权重参数w。

image-20221209170519833

image-20221209170617176

image-20221209170913255

image-20221209171050706

image-20221209171152826

image-20221209171517443

image-20221209171719637

image-20221209171807581

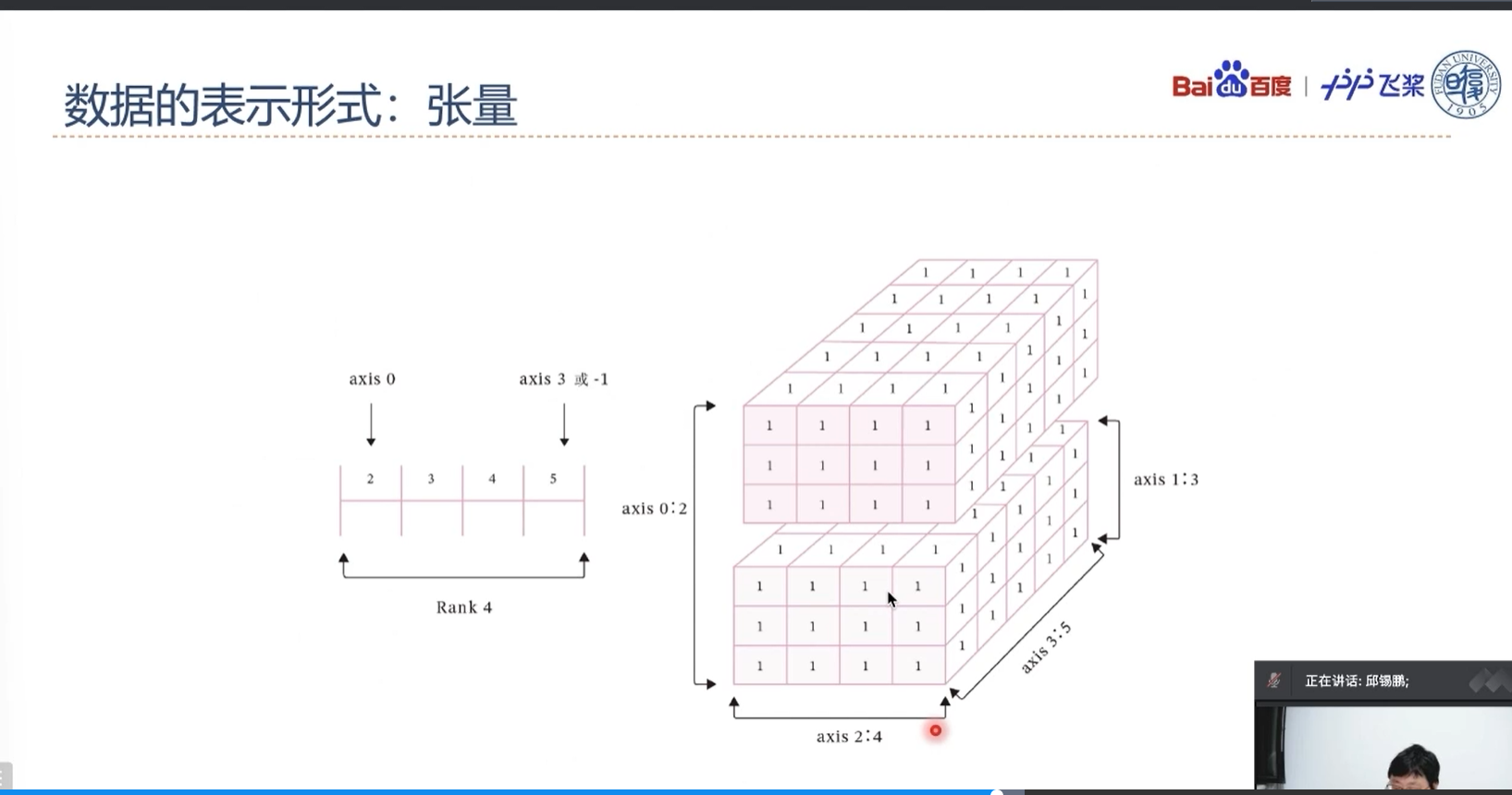
数据的表示形式：张量

image-20221209171932632

模型的基本单位：算子

image-20221209172120885

image-20221209172155193

image-20221209172243261

image-20221209172334081

image-20221209172402042

image-20221209172413995

image-20221209172451113

image-20221209184636787

image-20221209184730941

image-20221209184904577

1.2 - [视频] 直播回放——程军老师

image-20221209190201310

image-20221209190403077

image-20221209190439105

image-20221209190912554

image-20221209191043045

image-20221209191142578

resnet最常用的版本是resnet50，resnet后续的一些改进的版本有一些是对步长做优化。

image-20221209203557361

image-20221209203902367

image-20221209204026855

image-20221209204211326

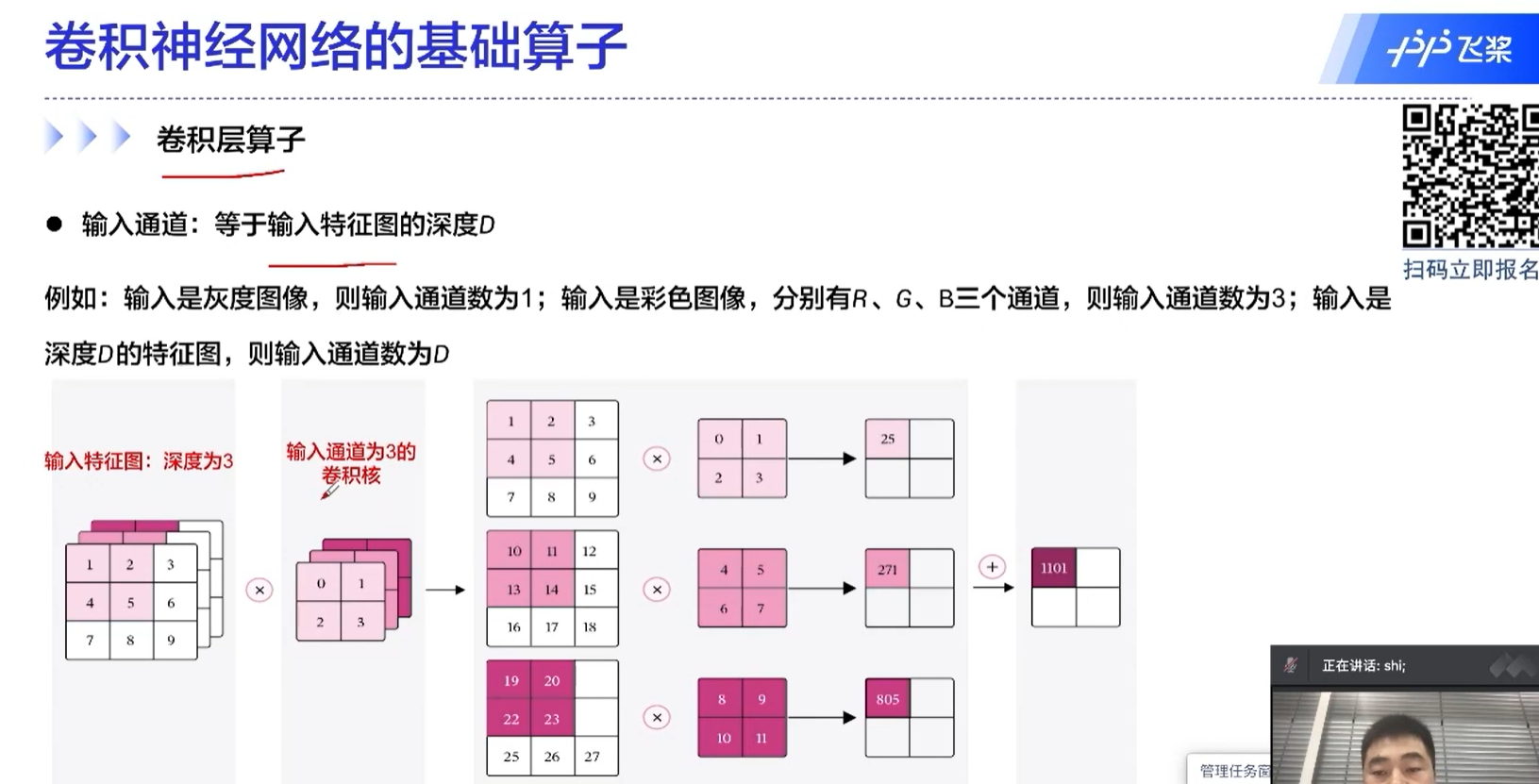
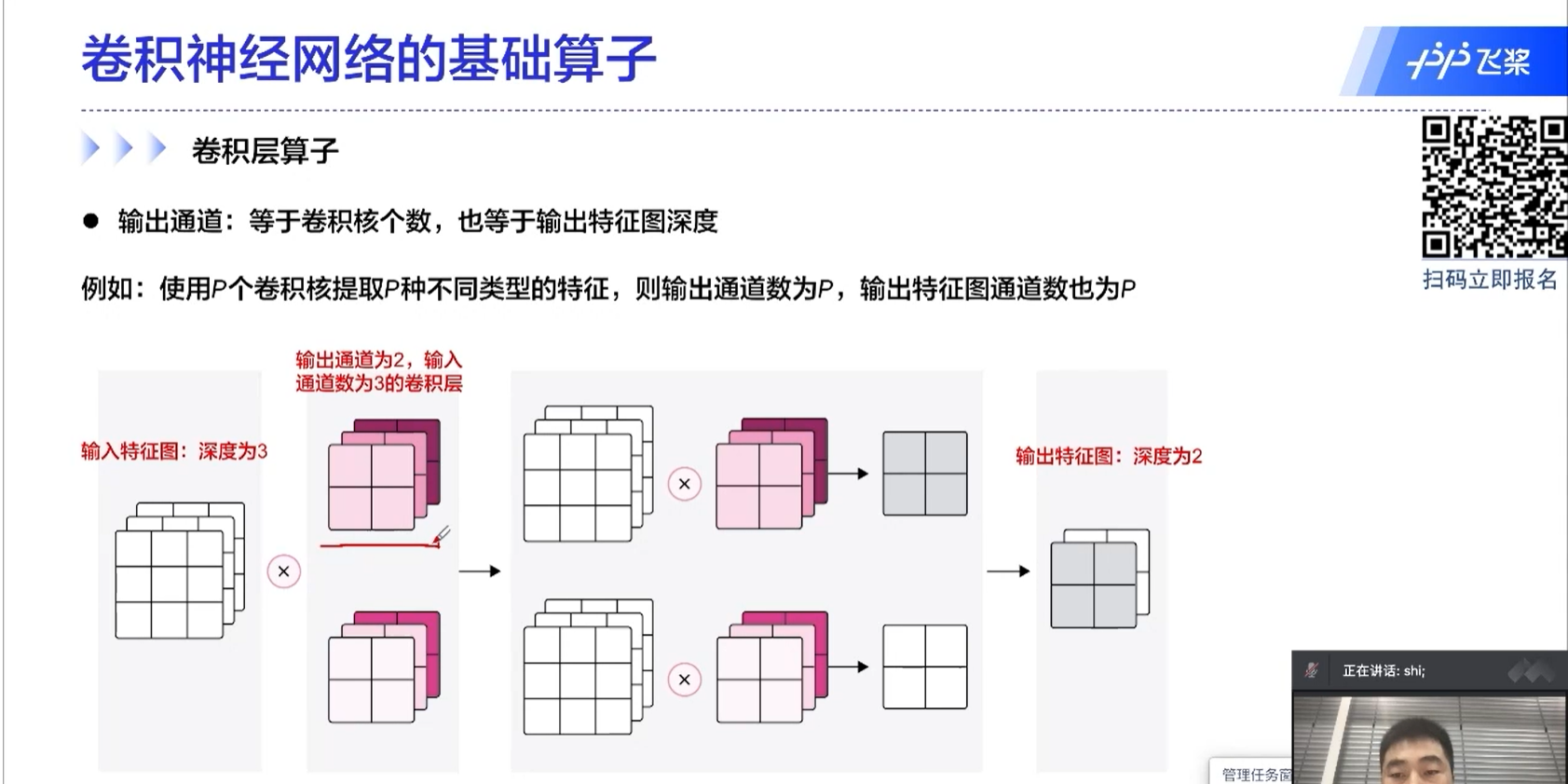
输出通道：等于卷积核的个数，也等于输出特征图的深度。

多通道卷积层算子的代码

image-20221209204457431

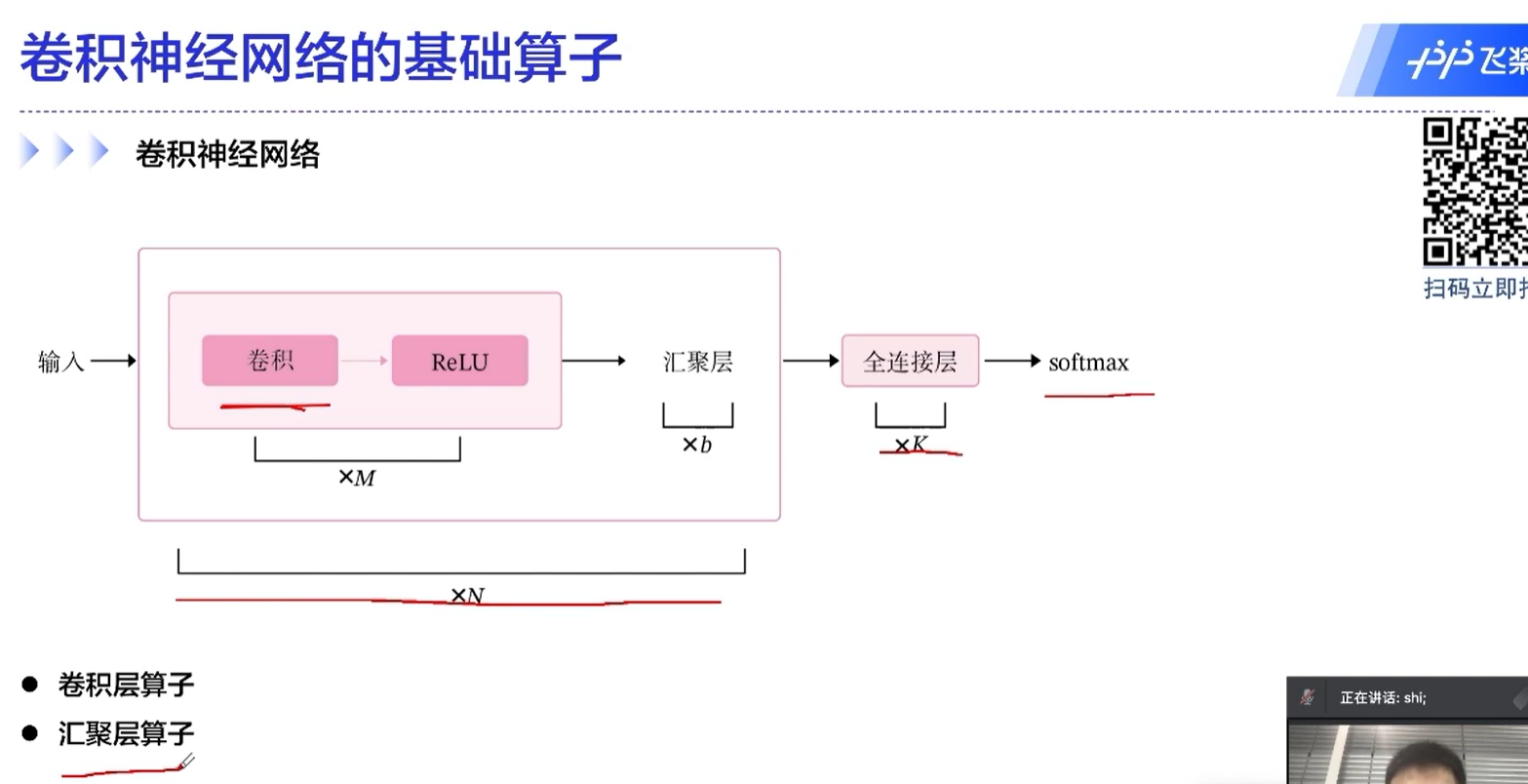
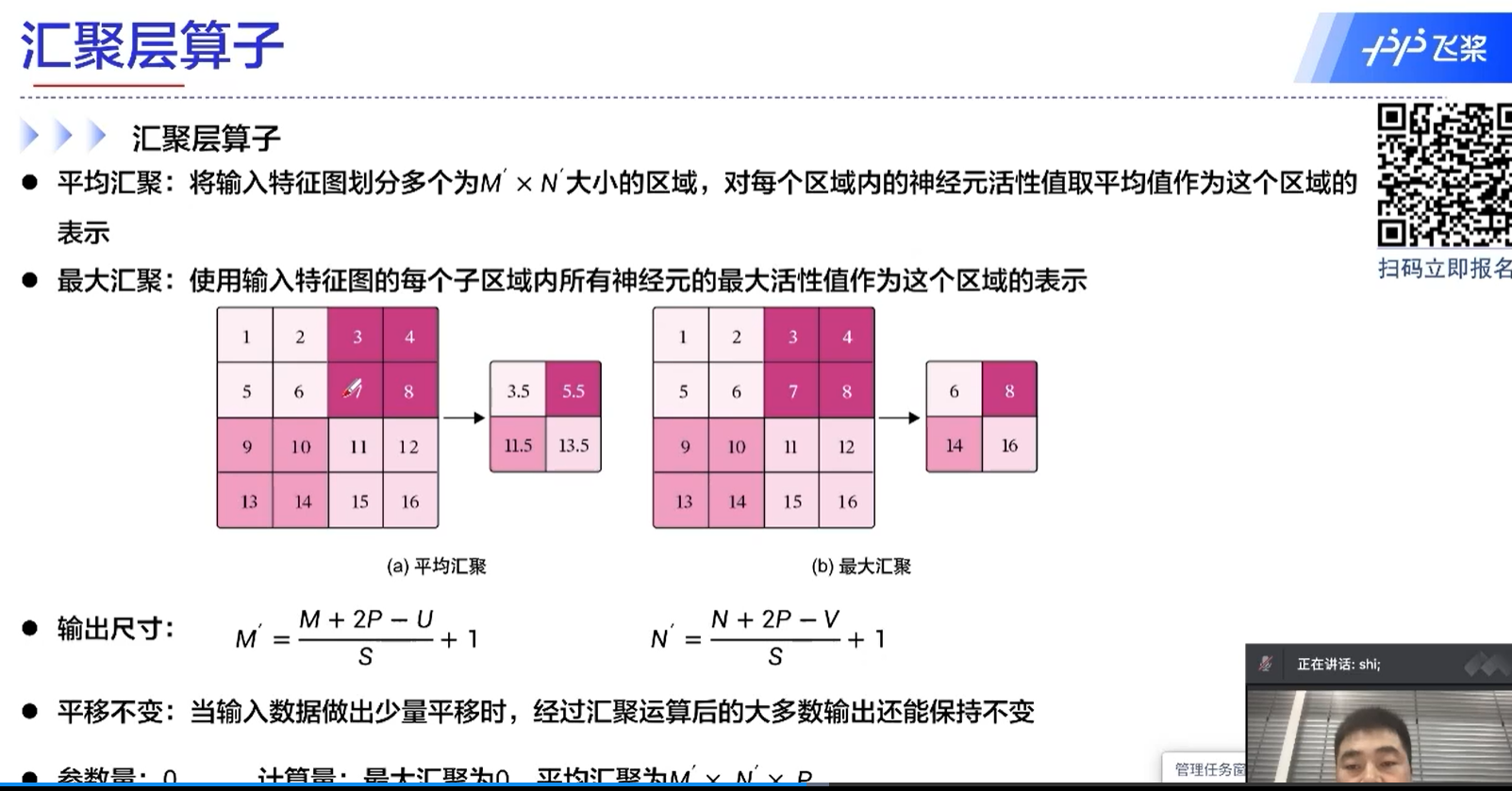
汇聚层算子

image-20221209204701684

汇聚层 = 池化层？

平均池化、最大池化

image-20221209205003669

image-20221209205908083

image-20221209210046272

image-20221209210241288

image-20221209210309555

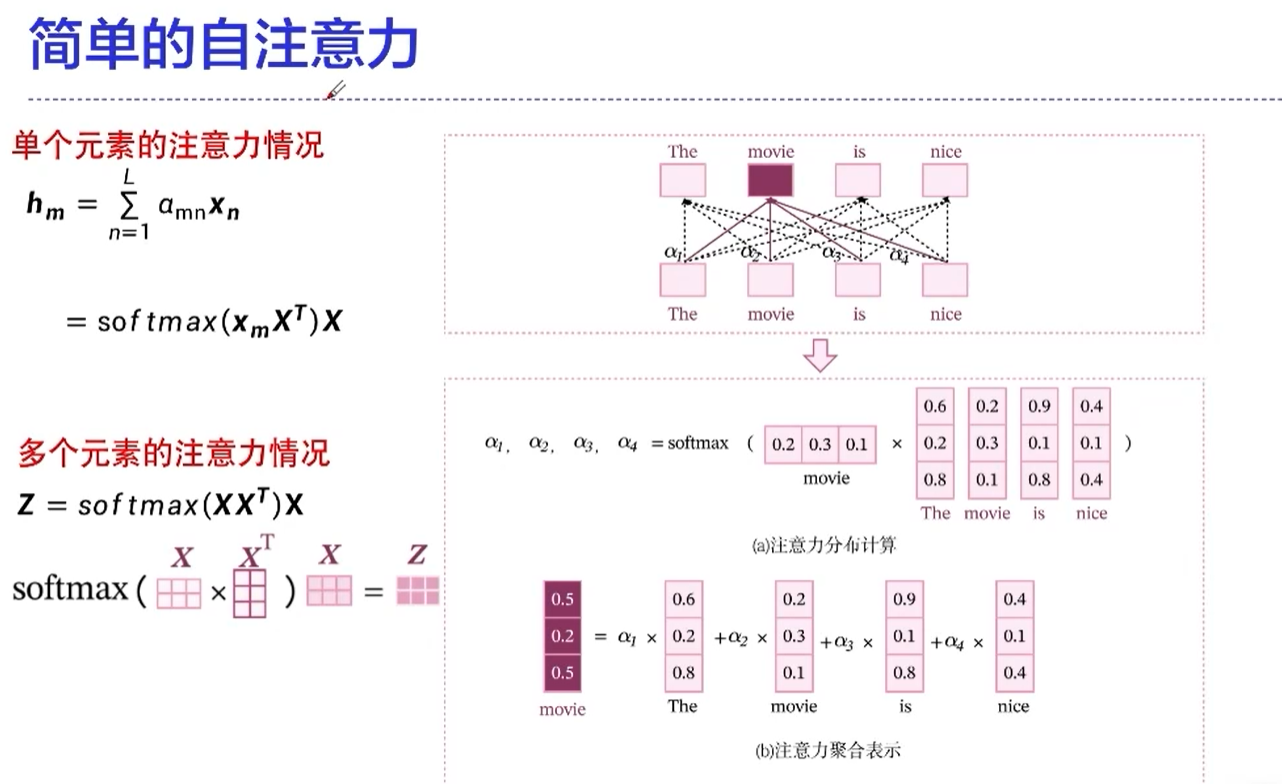
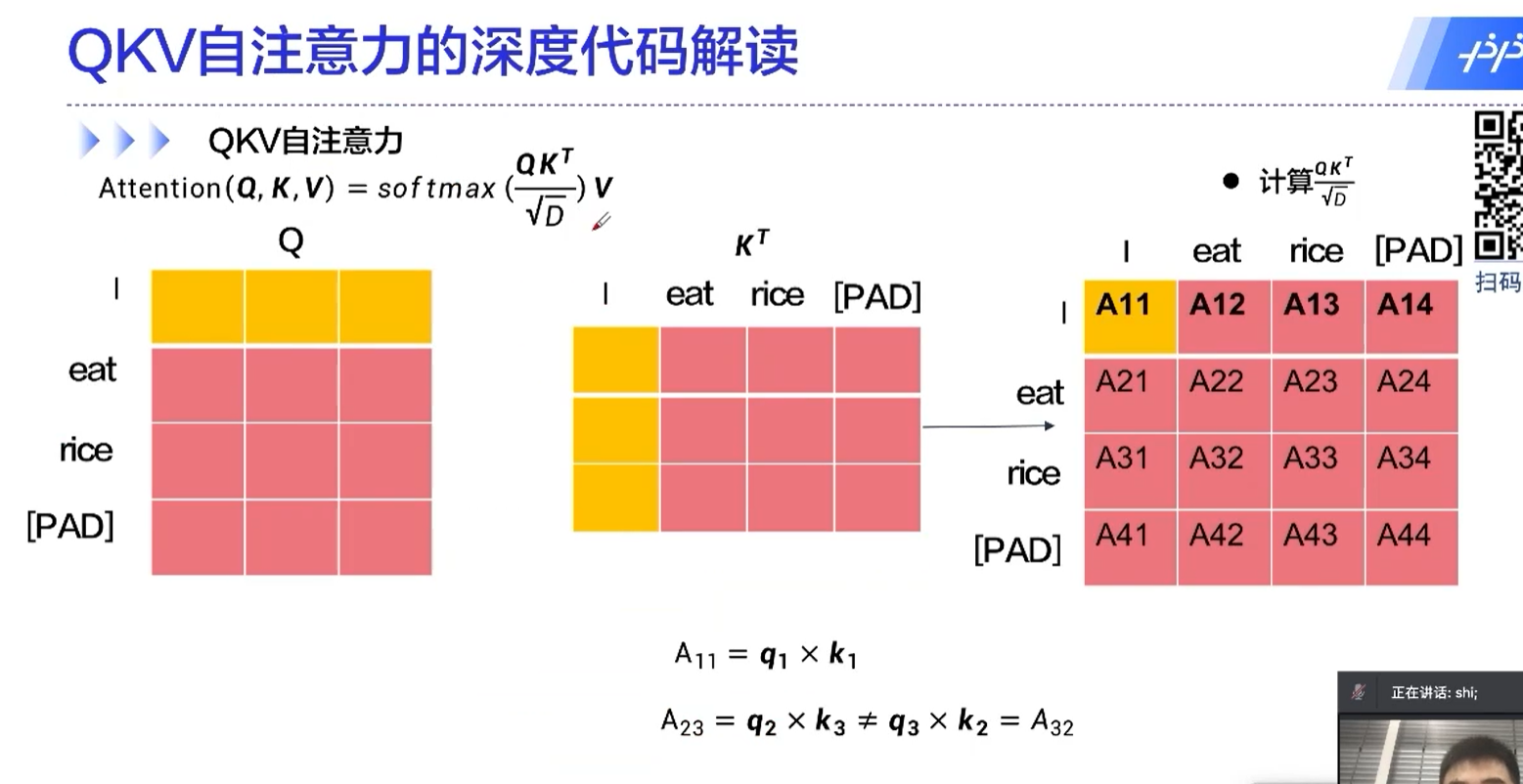
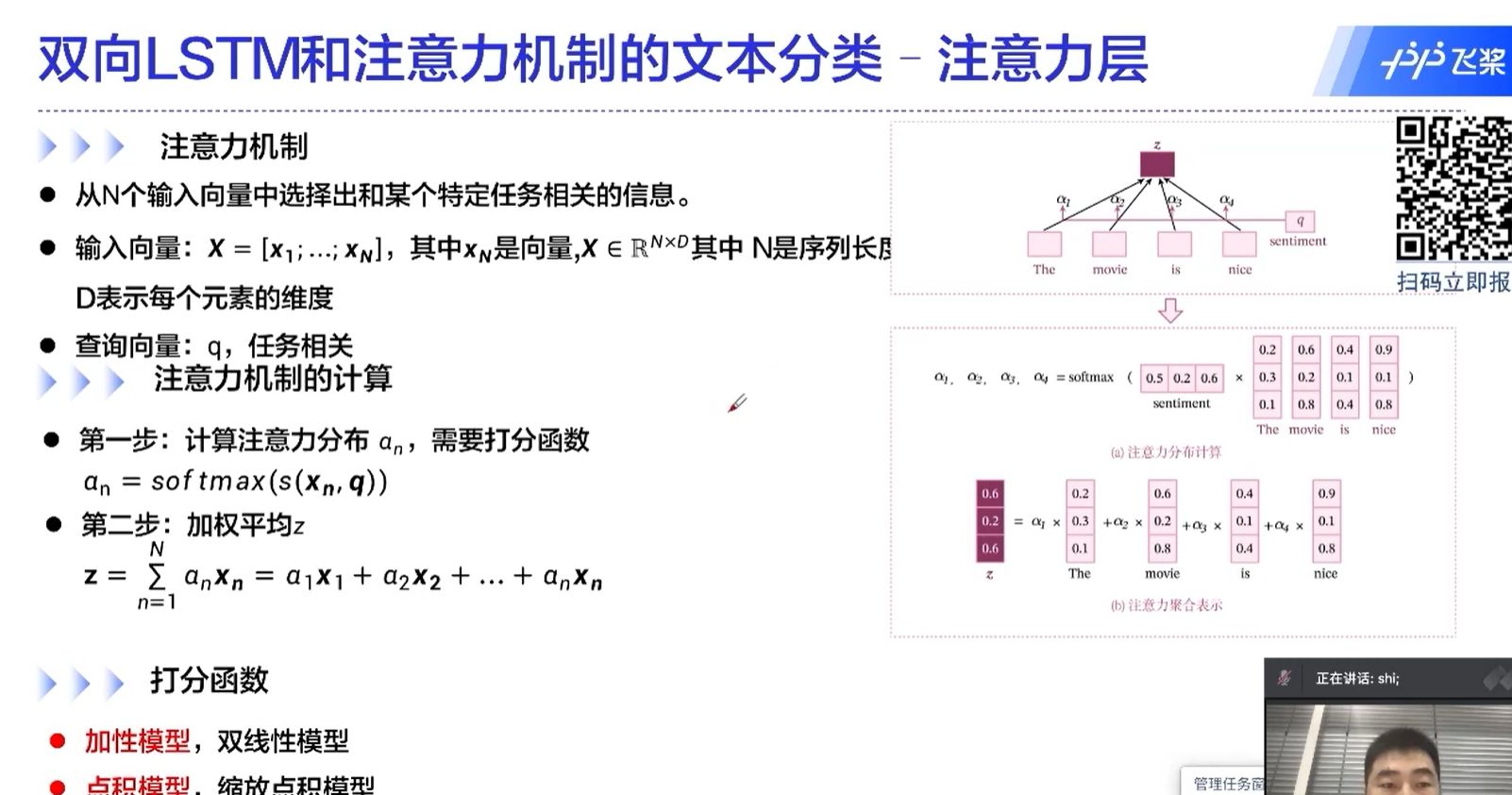
transformer的核心

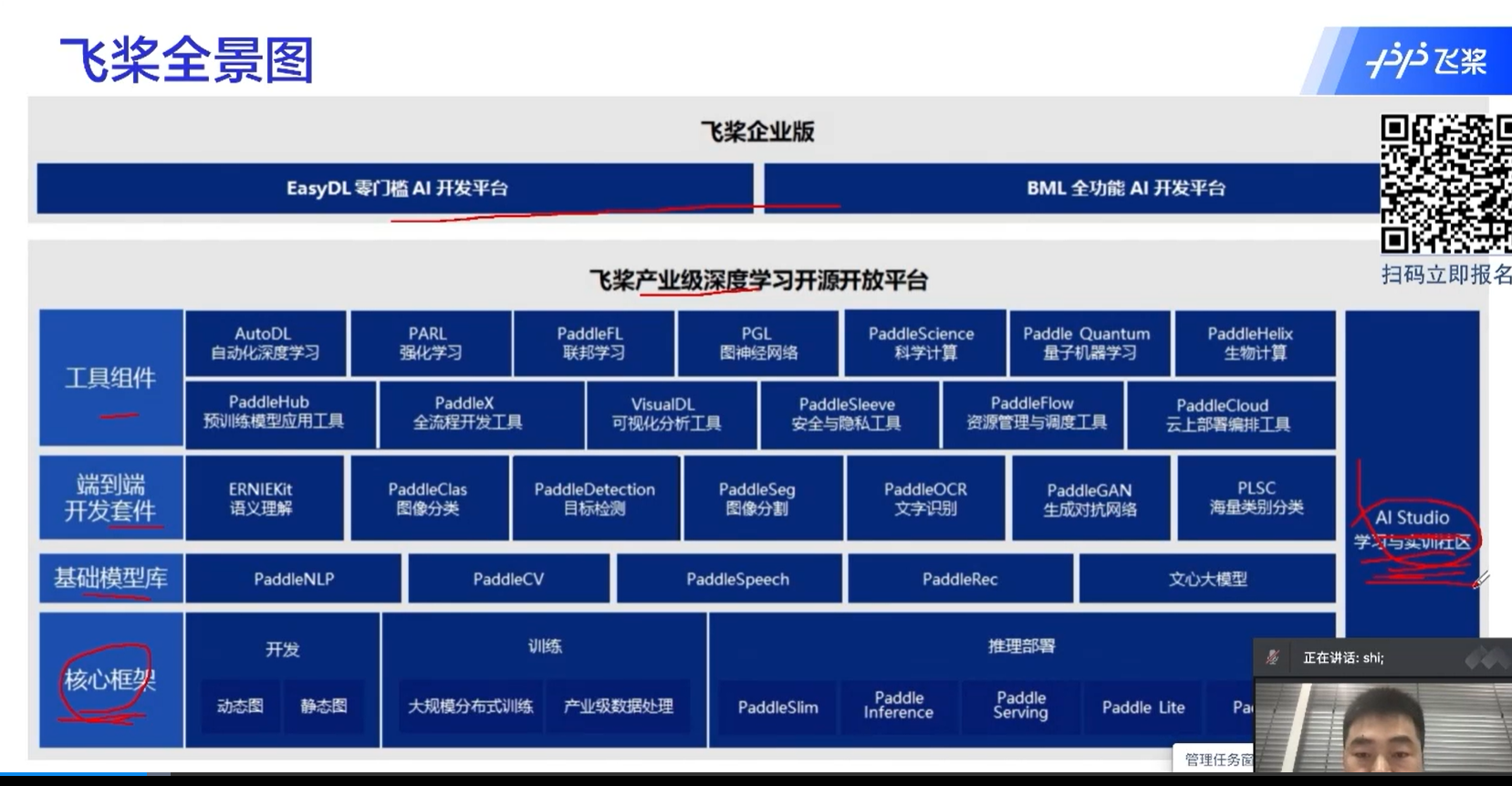
image-20221209210516027

image-20221209210809368

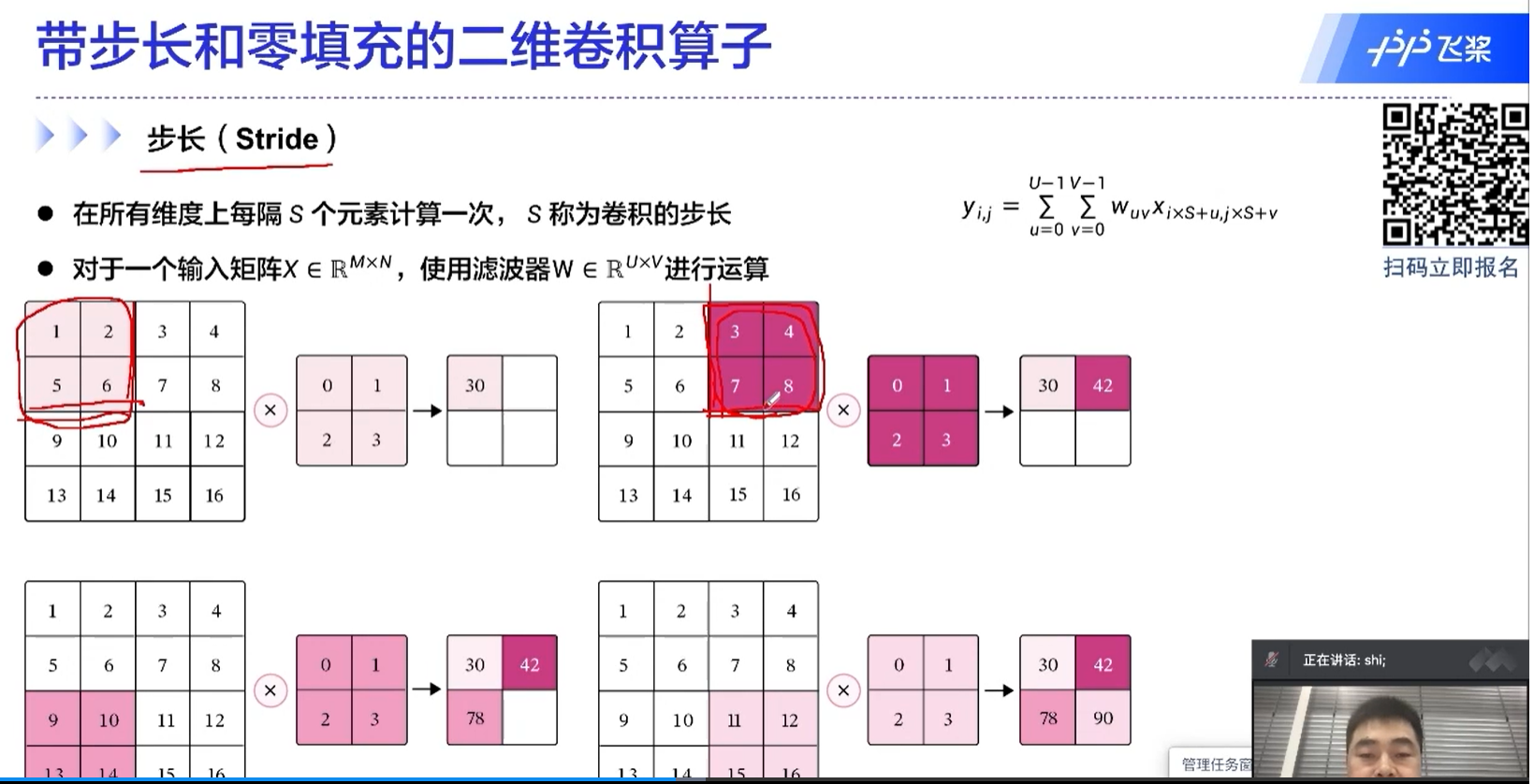
image-20221209210857085

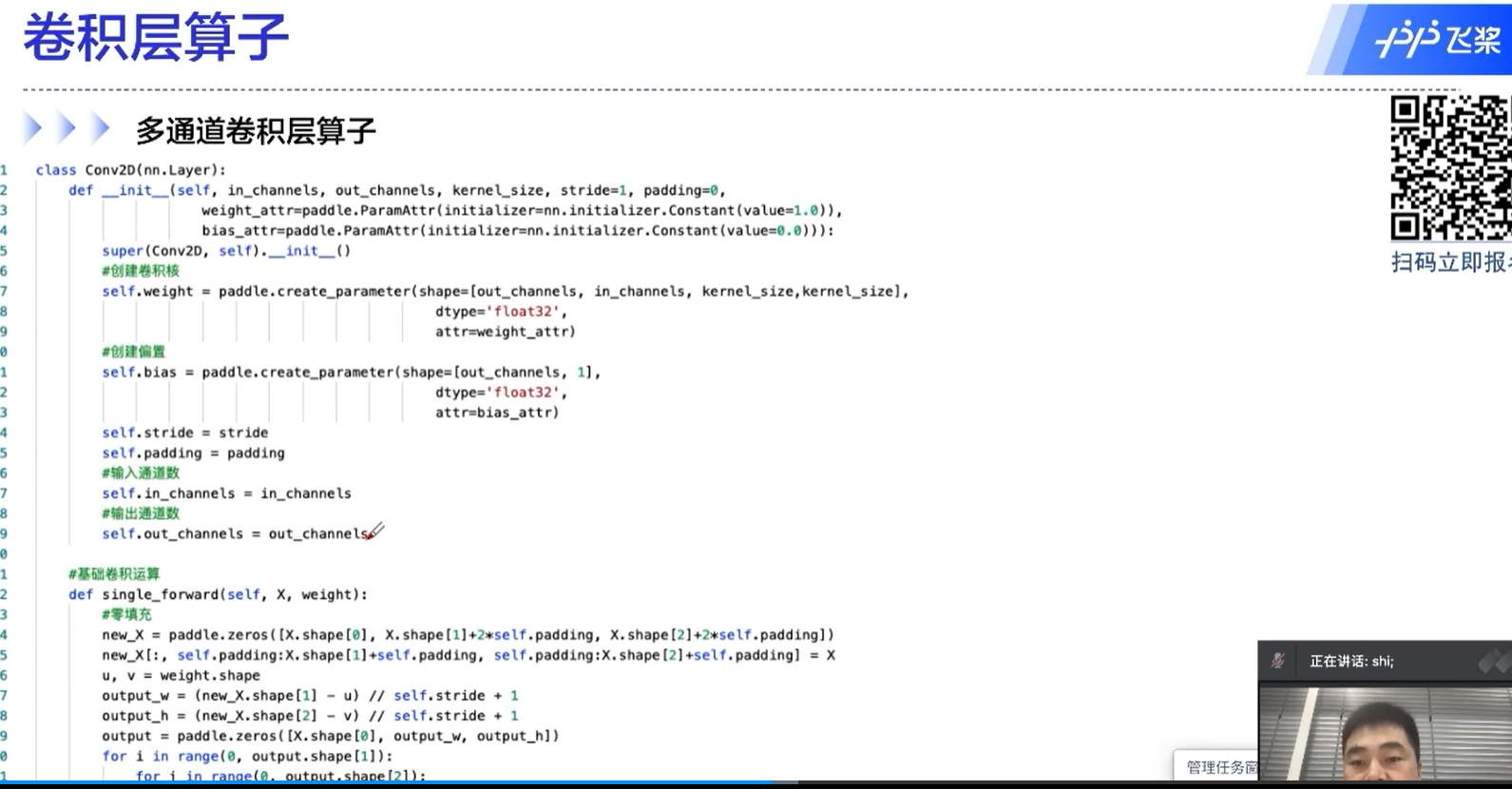
image-20221209211255275

image-20221209211448984

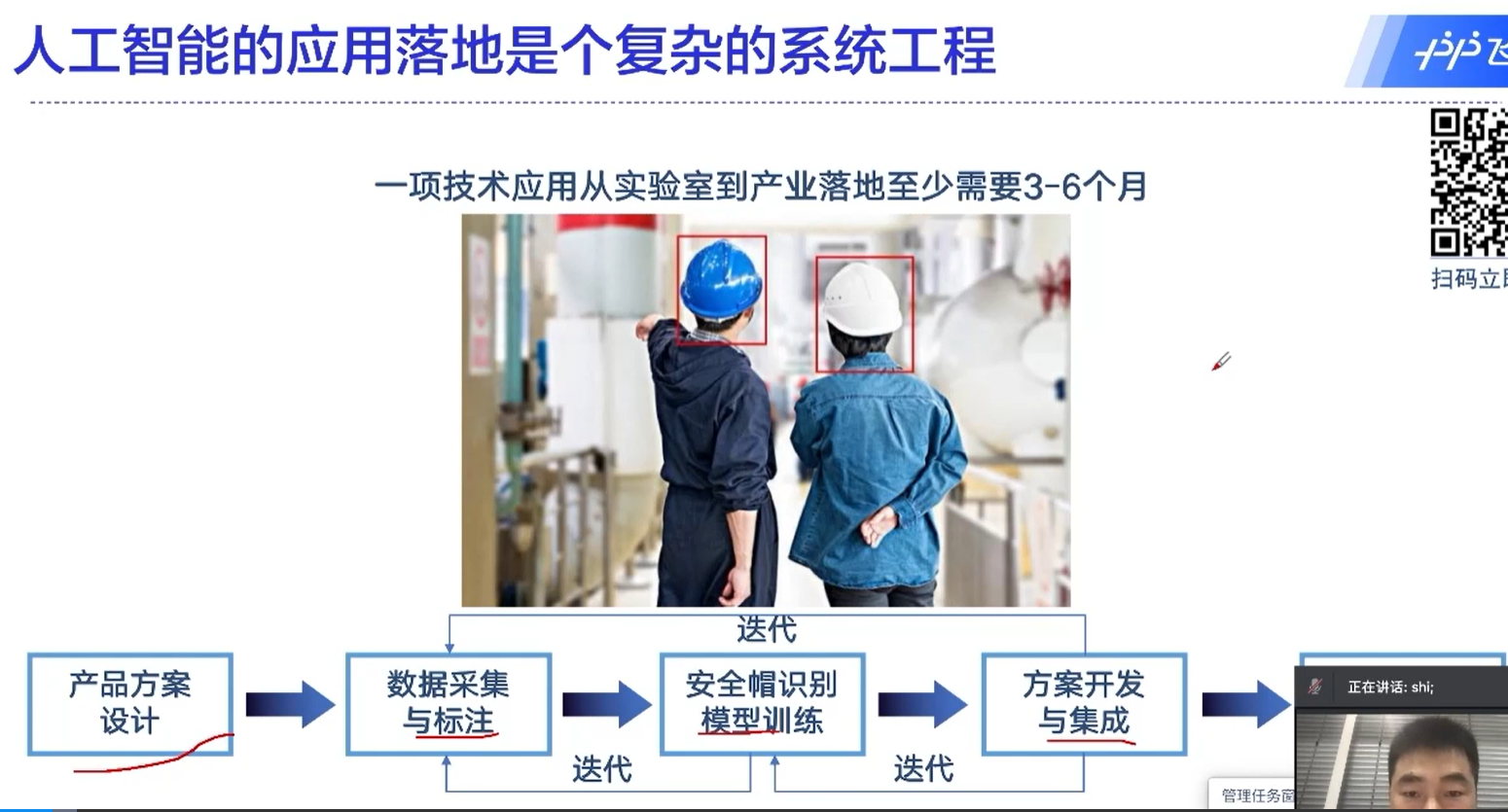
image-20221209211723963

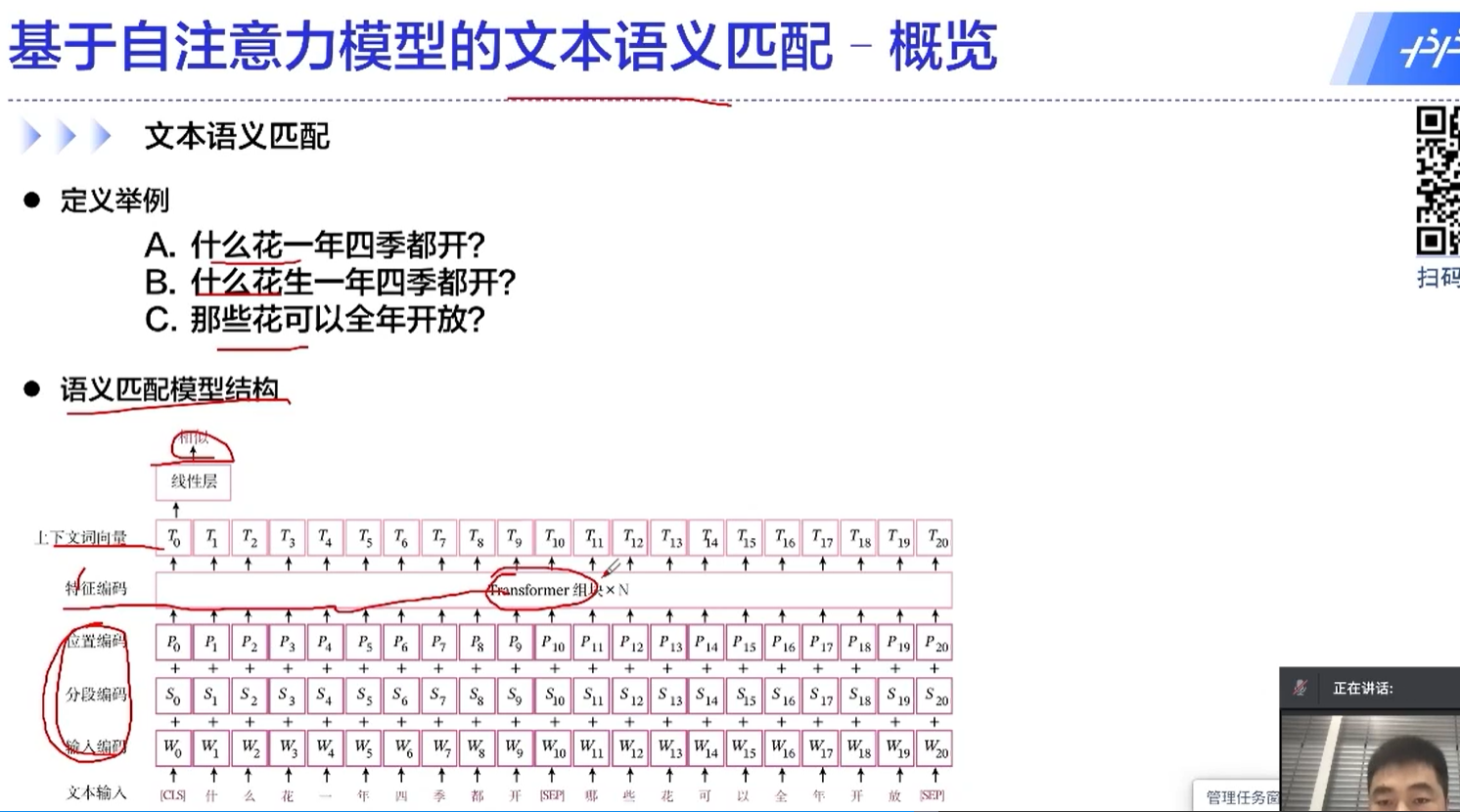
image-20221209211809857

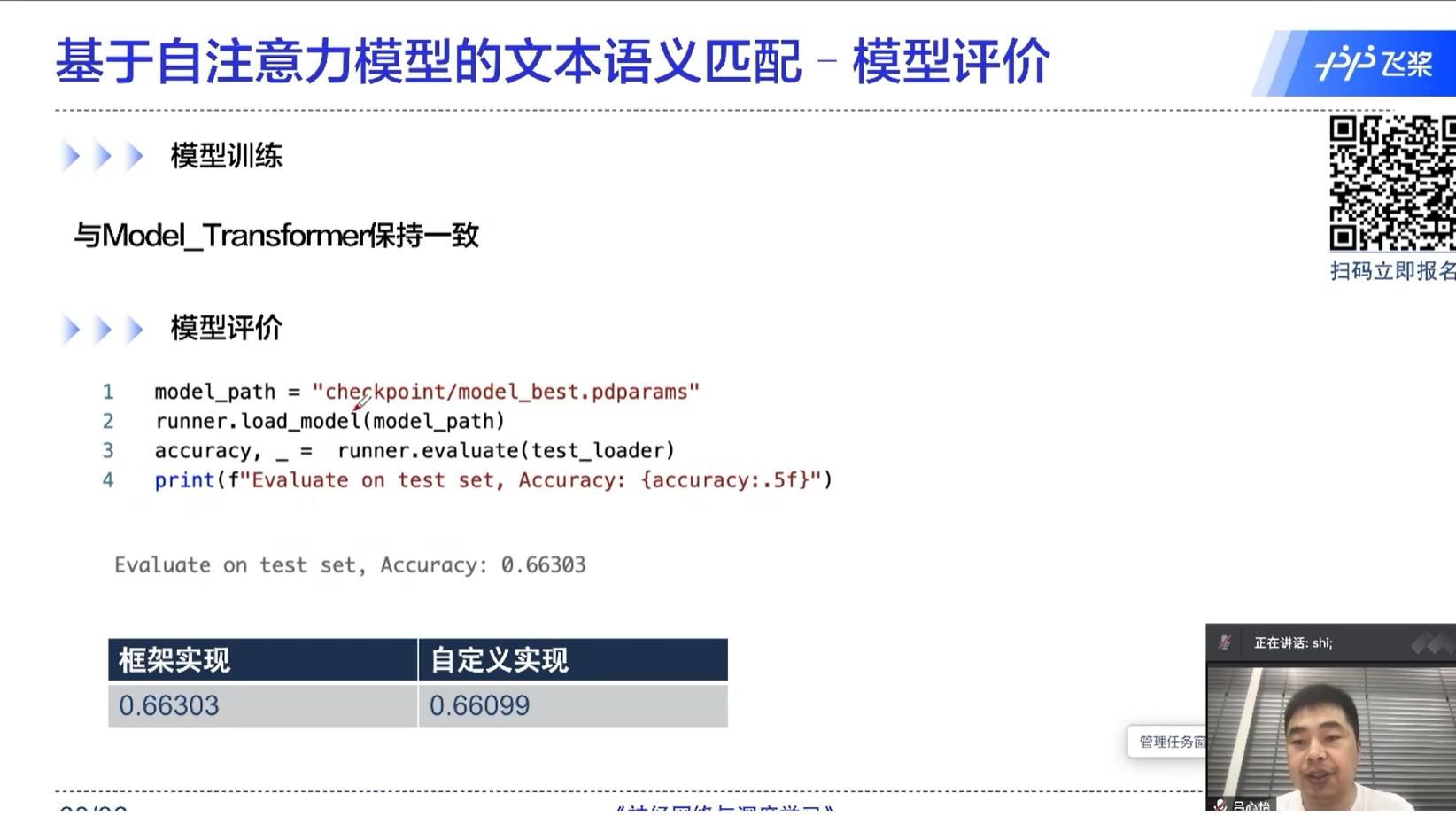
image-20221209212008942

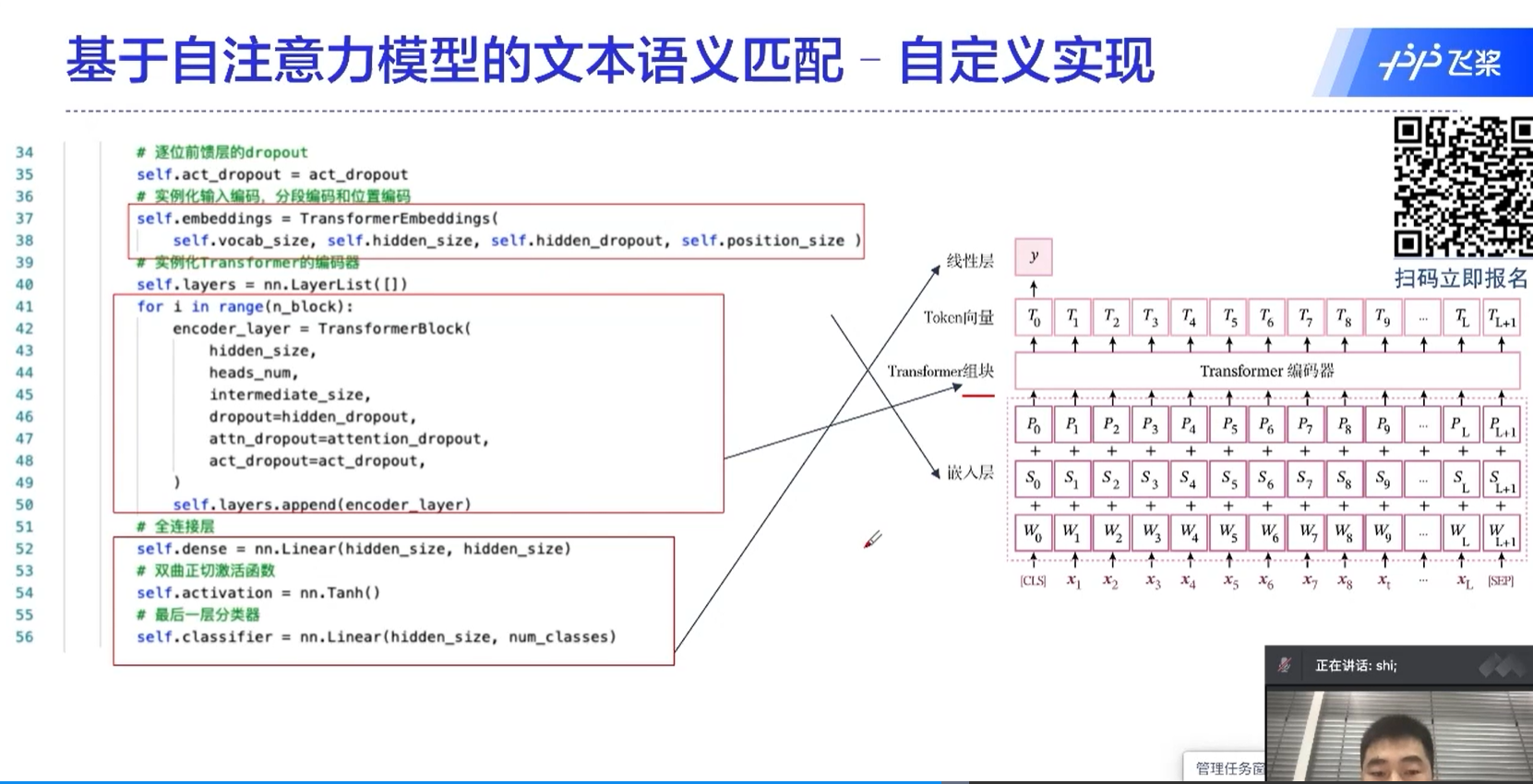
image-20221209213426769

自注意力机制中，一个元素是和所有的元素做运算的，这也是transformer为什么能够取得很好的效果的原因。

通过这种方式，不同于RNN的地方在于，不同的时间序列能够做信息的传递、融合；还有一个好处是这里面的运算是可以并行的

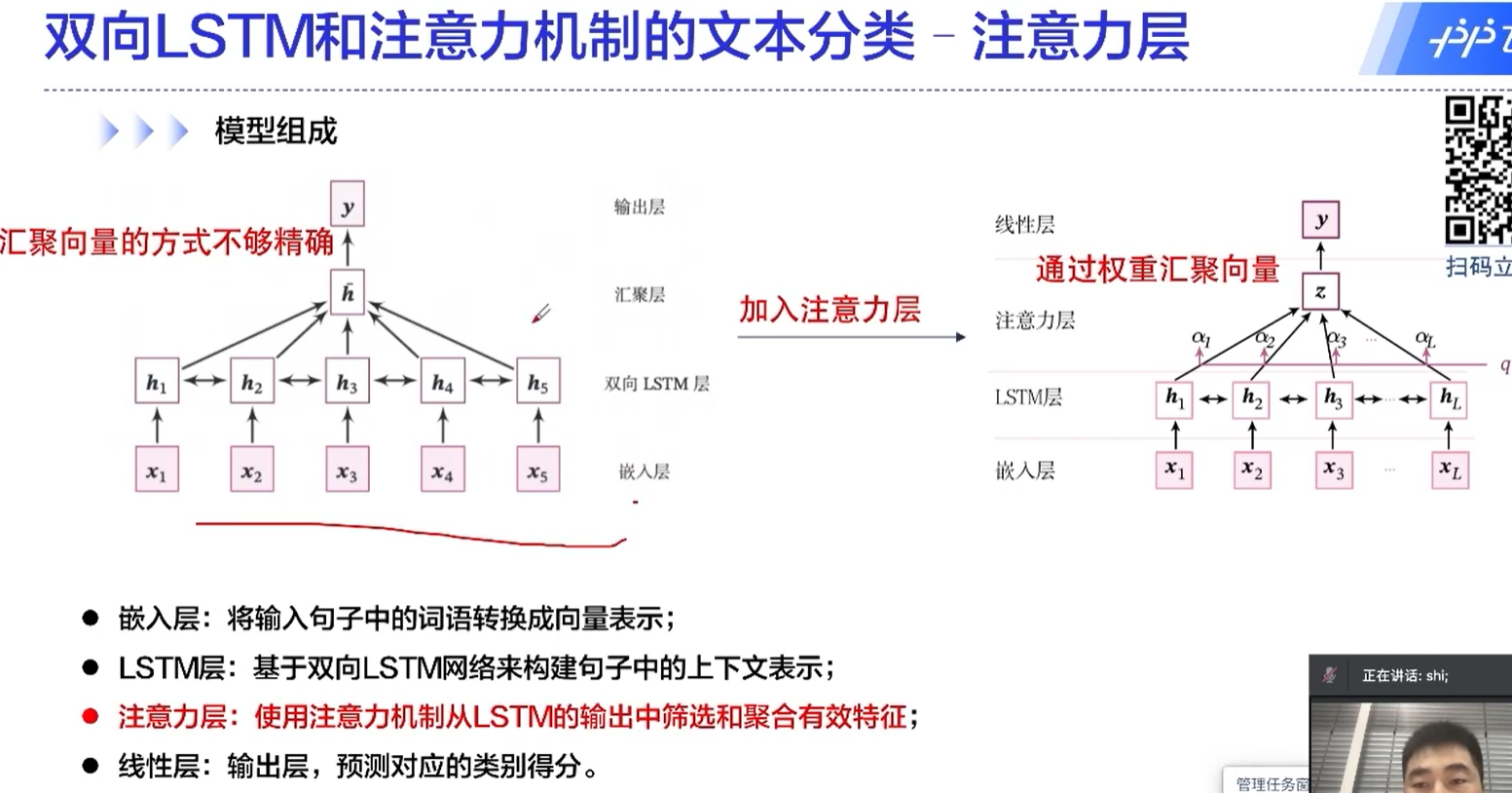
image-20221209213544884

image-20221209213957385

##↓↓↓############################↓↓↓

1.3 - [项目] 第1章：实践基础

在讲解本书主要内容之前，本章先对实践环节的基础知识进行介绍，主要介绍以下内容：

  • 张量（Tensor）：深度学习中表示和存储数据的主要形式。在动手实践机器学习之前，需要熟悉张量的概念、性质和运算规则，以及了解飞桨中张量的各种API。
  • 算子（Operator）：构建神经网络模型的基础组件。每个算子有前向和反向计算过程，前向计算对应一个数学函数，而反向计算对应这个数学函数的梯度计算。有了算子，我们就可以很方便地通过算子来搭建复杂的神经网络模型，而不需要手工计算梯度。

此外，本章还汇总了在本书中自定义的一些算术、数据集以及轻量级训练框架Runner类。

D（√）1.1 如何运行本书的代码

本书中代码有两种运行方式：本地运行AI Studio运行。下面我们分别介绍两种运行方式的环境准备及操作方法。

（√）1.1.1 本地运行
（√）1.1.2 AI studio运行√

AI Studio是基于飞桨的人工智能学习与实训社区，提供免费的算力支持，本书的内容在AI Studio上提供配套的BML Codelab项目。BML Codelab是面向个人和企业开发者的AI开发工具，基于Jupyter提供了在线的交互式开发环境。

BML Codelab目前默认使用飞桨2.2.2版本，无须额外安装。如图1.1所示，通过选择“启动环境”→\rightarrow→“基础版”即可在CPU环境下运行，选择“至尊版GPU”即可在32G RAM的Tesla V100上运行代码，至尊版GPU每天有8小时的免费使用时间。

D（√）1.2 张量

在深度学习框架中，数据经常用张量(Tensor)的形式来存储。张量是矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量为向量，2阶张量为矩阵。如果你对

Numpy熟悉，那么张量是类似于Numpy的多维数组(ndarray)的概念，可以具有任意多的维度。

张量中元素的类型可以是布尔型数据、整数、浮点数或者复数，但同一张量中所有元素的数据类型均相同。因此我们可以给张量定义一个数据类型(dtype)来表

示其元素的类型。

E（√）1.2.1 创建张量
F（√）1.2.1.1 指定数据创建张量

（1）指定数据，创建一维张量

1
2
3
4
5
# 导入PaddlePaddle
import paddle
# 创建一维Tensor
ndim_1_Tensor = paddle.to_tensor([2.0, 3.0, 4.0])
print(ndim_1_Tensor)

（2）指定数据，创建二维矩阵

1
2
3
4
# 创建二维Tensor
ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0, 3.0],
                                  [4.0, 5.0, 6.0]])
print(ndim_2_Tensor)

（3）指定数据，创建多维张量

1
2
3
4
5
6
# 创建多维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)

注意：张量在任何一个维度上的元素数量必须相等

F（√）1.2.1.2 指定形状创建

如果要创建一个指定形状、元素数据相同的张量，可以使用paddle.zeros、paddle.ones、paddle.full等API。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
m, n = 2, 3

# 使用paddle.zeros创建数据全为0，形状为[m, n]的Tensor
zeros_Tensor = paddle.zeros([m, n])

# 使用paddle.ones创建数据全为1，形状为[m, n]的Tensor
ones_Tensor = paddle.ones([m, n])

# 使用paddle.full创建数据全为指定值，形状为[m, n]的Tensor，这里我们指定数据为10
full_Tensor = paddle.full([m, n], 10)

print('zeros Tensor: ', zeros_Tensor)
print('ones Tensor: ', ones_Tensor)
print('full Tensor: ', full_Tensor)
F（√）1.2.1.3 指定区间创建

如果要在指定区间内创建张量，可以使用paddle.arange、paddle.linspace等API。

1
2
3
4
5
6
7
8
# 使用paddle.arange创建以步长step均匀分隔数值区间[start, end)的一维Tensor
arange_Tensor = paddle.arange(start=1, end=5, step=1)

# 使用paddle.linspace创建以元素个数num均匀分隔数值区间[start, stop]的Tensor
linspace_Tensor = paddle.linspace(start=1, stop=5, num=5)

print('arange Tensor: ', arange_Tensor)
print('linspace Tensor: ', linspace_Tensor)
E（√）1.2.2 张量的属性
F（√）1.2.2.1 张量的形状
1
2
3
4
5
6
7
ndim_4_Tensor = paddle.ones([2, 3, 4, 5])

print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])
print('Number of elements in Tensor: ', ndim_4_Tensor.size)
1
2
3
4
5
Number of dimensions: 4
Shape of Tensor: [2, 3, 4, 5]
Elements number along axis 0 of Tensor: 2
Elements number along the last axis of Tensor: 5
Number of elements in Tensor:  120
F（√）1.2.2.2 形状的改变

总结：

使用reshape方法和unsqueeze方法改变张量的shape

除了查看张量的形状外，重新设置张量的在实际编程中也具有重要意义，飞桨提供了paddle.reshape接口来改变张量的形状。

1
2
3
4
5
6
7
8
9
10
11
12
# 定义一个shape为[3,2,5]的三维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]],
                                  [[21, 22, 23, 24, 25],
                                   [26, 27, 28, 29, 30]]])
print("the shape of ndim_3_Tensor:", ndim_3_Tensor.shape)

# paddle.reshape 可以保持在输入数据不变的情况下，改变数据形状。这里我们设置reshape为[2,5,3]
reshape_Tensor = paddle.reshape(ndim_3_Tensor, [2, 5, 3])
print("After reshape:", reshape_Tensor)
1
2
3
4
5
6
7
8
9
10
11
12
13
the shape of ndim_3_Tensor: [3, 2, 5]
After reshape: Tensor(shape=[2, 5, 3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [[[1 , 2 , 3 ],
         [4 , 5 , 6 ],
         [7 , 8 , 9 ],
         [10, 11, 12],
         [13, 14, 15]],

        [[16, 17, 18],
         [19, 20, 21],
         [22, 23, 24],
         [25, 26, 27],
         [28, 29, 30]]])

从输出结果看，将张量从[3, 2, 5]的形状reshape为[2, 5, 3]的形状时，张量内的数据不会发生改变，元素顺序也没有发生改变，只有数据形状发生了改变。

笔记

使用reshape时存在一些技巧，比如：

  • -1表示这个维度的值是从张量的元素总数和剩余维度推断出来的。因此，有且只有一个维度可以被设置为-1。
  • 0表示实际的维数是从张量的对应维数中复制出来的，因此shape中0所对应的索引值不能超过张量的总维度。

分别对上文定义的ndim_3_Tensor进行reshape为[-1]和reshape为[0, 5, 2]两种操作，观察新张量的形状。

1
2
3
4
new_Tensor1 = ndim_3_Tensor.reshape([-1])
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Tensor2 = ndim_3_Tensor.reshape([0, 5, 2])
print('new Tensor 2 shape: ', new_Tensor2.shape)
1
2
new Tensor 1 shape:  [30]
new Tensor 2 shape:  [3, 5, 2]

从输出结果看，第一行代码中的第一个reshape操作将张量reshape为元素数量为30的一维向量；第四行代码中的第二个reshape操作中，0对应的维度的元素个数与原张量在该维度上的元素个数相同。

除使用paddle.reshape进行张量形状的改变外，还可以通过paddle.unsqueeze将张量中的一个或多个维度中插入尺寸为1的维度。

1
2
3
4
5
ones_Tensor = paddle.ones([5, 10])
new_Tensor1 = paddle.unsqueeze(ones_Tensor, axis=0)
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Tensor2 = paddle.unsqueeze(ones_Tensor, axis=[1, 2])
print('new Tensor 2 shape: ', new_Tensor2.shape)
1
2
new Tensor 1 shape:  [1, 5, 10]
new Tensor 2 shape:  [5, 1, 1, 10]
F（√）1.2.2.3 张量的数据类型

飞桨中可以通过Tensor.dtype来查看张量的数据类型，类型支持bool、float16、float32、float64、uint8、int8、int16、int32、int64和复数类型数据。

1）通过Python元素创建的张量，可以通过dtype来指定数据类型，如果未指定：

  • 对于Python整型数据，则会创建int64型张量。
  • 对于Python浮点型数据，默认会创建float32型张量。

2）通过Numpy数组创建的张量，则与其原来的数据类型保持相同。通过paddle.to_tensor()函数可以将Numpy数组转化为张量。

1
2
3
# 使用paddle.to_tensor通过已知数据来创建一个Tensor
print("Tensor dtype from Python integers:", paddle.to_tensor(1).dtype)
print("Tensor dtype from Python floating point:", paddle.to_tensor(1.0).dtype)
1
2
Tensor dtype from Python integers: paddle.int64
Tensor dtype from Python floating point: paddle.float32

如果想改变张量的数据类型，可以通过调用paddle.castAPI来实现。

1
2
3
4
5
# 定义dtype为float32的Tensor
float32_Tensor = paddle.to_tensor(1.0)
# paddle.cast可以将输入数据的数据类型转换为指定的dtype并输出。支持输出和输入数据类型相同。
int64_Tensor = paddle.cast(float32_Tensor, dtype='int64')
print("Tensor after cast to int64:", int64_Tensor.dtype)
1
Tensor after cast to int64: paddle.int64
F（√）1.2.2.4 张量的设备位置

初始化张量时可以通过place来指定其分配的设备位置，可支持的设备位置有三种：CPU、GPU和固定内存。

固定内存也称为不可分页内存或锁页内存，它与GPU之间具有更高的读写效率，并且支持异步传输，这对网络整体性能会有进一步提升，但它的缺点是分配空间过多时可能会降低主机系统的性能，因为它减少了用于存储虚拟内存数据的可分页内存。当未指定设备位置时，张量默认设备位置和安装的飞桨版本一致，如安装了GPU版本的飞桨，则设备位置默认为GPU。

如下代码分别创建了CPU、GPU和固定内存上的张量，并通过Tensor.place查看张量所在的设备位置。

1
2
3
4
5
6
7
8
9
10
# 创建CPU上的Tensor
cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
# 通过Tensor.place查看张量所在设备位置
print('cpu Tensor: ', cpu_Tensor.place)
# 创建GPU上的Tensor
gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print('gpu Tensor: ', gpu_Tensor.place)
# 创建固定内存上的Tensor
pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print('pin memory Tensor: ', pin_memory_Tensor.place)
1
2
3
cpu Tensor:  CPUPlace
gpu Tensor:  CUDAPlace(0)
pin memory Tensor:  CUDAPinnedPlace
E（√）1.2.3 张量与Numpy数组转换

张量和Numpy数组可以相互转换。第1.2.2.3节中我们了解到paddle.to_tensor()函数可以将Numpy数组转化为张量，也可以通过Tensor.numpy()函数将张量转化为Numpy数组。

1
2
3
4
ndim_1_Tensor = paddle.to_tensor([1., 2.])
# 将当前 Tensor 转化为 numpy.ndarray
print('Tensor to convert: ', ndim_1_Tensor.numpy())
print(type(ndim_1_Tensor.numpy()))
1
2
Tensor to convert:  [1. 2.]
<class 'numpy.ndarray'>
E（√）1.2.4 张量的访问
F（√）1.2.4.1 索引和切片

我们可以通过索引或切片方便地访问或修改张量。飞桨使用标准的Python索引规则与Numpy索引规则，具有以下特点：

  • 基于0−n0-n0−n的下标进行索引，如果下标为负数，则从尾部开始计算。
  • 通过冒号“:”分隔切片参数start:stop:step来进行切片操作，也就是访问start到stop范围内的部分元素并生成一个新的序列。其中start为切片的起始位置，stop为切片的截止位置，step是切片的步长，这三个参数均可缺省。
F（√）1.2.4.2 访问张量
1
2
3
4
5
6
7
8
9
10
# 定义1个一维Tensor
ndim_1_Tensor = paddle.to_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])

print("Origin Tensor:", ndim_1_Tensor)
print("First element:", ndim_1_Tensor[0])
print("Last element:", ndim_1_Tensor[-1])
print("All element:", ndim_1_Tensor[:])
print("Before 3:", ndim_1_Tensor[:3])
print("Interval of 3:", ndim_1_Tensor[::3])
print("Reverse:", ndim_1_Tensor[::-1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Origin Tensor: Tensor(shape=[9], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2, 3, 4, 5, 6, 7, 8])
First element: Tensor(shape=[1], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0])
Last element: Tensor(shape=[1], dtype=int64, place=CPUPlace, stop_gradient=True,
       [8])
All element: Tensor(shape=[9], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2, 3, 4, 5, 6, 7, 8])
Before 3: Tensor(shape=[3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 1, 2])
Interval of 3: Tensor(shape=[3], dtype=int64, place=CPUPlace, stop_gradient=True,
       [0, 3, 6])
Reverse: Tensor(shape=[9], dtype=int64, place=CPUPlace, stop_gradient=True,
       [8, 7, 6, 5, 4, 3, 2, 1, 0])

针对二维及以上维度的张量，在多个维度上进行索引或切片。索引或切片的第一个值对应第0维，第二个值对应第1维，以此类推，如果某个维度上未指定索引，则默认为“:”。

1
2
3
4
5
6
7
8
9
10
11
# 定义1个二维Tensor
ndim_2_Tensor = paddle.to_tensor([[0, 1, 2, 3],
                                  [4, 5, 6, 7],
                                  [8, 9, 10, 11]])
print("Origin Tensor:", ndim_2_Tensor)
print("First row:", ndim_2_Tensor[0])# 第一行
print("First row:", ndim_2_Tensor[0, :])# 第一行
print("First column:", ndim_2_Tensor[:, 0]) # 第一列
print("Last column:", ndim_2_Tensor[:, -1]) # 最后一列
print("All element:", ndim_2_Tensor[:]) # 全部
print("First row and second column:", ndim_2_Tensor[0, 1]) # 第一行，第二列
F（√）1.2.4.3 修改张量

与访问张量类似，可以在单个或多个轴上通过索引或切片操作来修改张量。

提醒
慎重通过索引或切片操作来修改张量，此操作仅会原地修改该张量的数值，且原值不会被保存。如果被修改的张量参与梯度计算，将仅会使用修改后的数值，这可能会给梯度计算引入风险。

1
2
3
4
5
6
7
8
9
10
11
12
# 定义1个二维Tensor
ndim_2_Tensor = paddle.ones([2, 3], dtype='float32')
print('Origin Tensor: ', ndim_2_Tensor)
# 修改第1维为0
ndim_2_Tensor[0] = 0
print('change Tensor: ', ndim_2_Tensor)
# 修改第1维为2.1
ndim_2_Tensor[0:1] = 2.1
print('change Tensor: ', ndim_2_Tensor)
# 修改全部Tensor
ndim_2_Tensor[...] = 3
print('change Tensor: ', ndim_2_Tensor)
1
2
3
4
5
6
7
8
9
10
11
12
Origin Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[1., 1., 1.],
        [1., 1., 1.]])
change Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0., 0., 0.],
        [1., 1., 1.]])
change Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[2.09999990, 2.09999990, 2.09999990],
        [1.        , 1.        , 1.        ]])
change Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[3., 3., 3.],
        [3., 3., 3.]])
E（√）1.2.5 张量的运算

张量支持包括基础数学运算、逻辑运算、矩阵运算等100余种运算操作，以加法为例，有如下两种实现方式：
1）使用飞桨API paddle.add(x,y)。
2）使用张量类成员函数x.add(y)。

1
2
3
4
5
6
7
# 定义两个Tensor
x = paddle.to_tensor([[1.1, 2.2], [3.3, 4.4]], dtype="float64")
y = paddle.to_tensor([[5.5, 6.6], [7.7, 8.8]], dtype="float64")
# 第一种调用方法，paddle.add逐元素相加算子，并将各个位置的输出元素保存到返回结果中
print('Method 1: ', paddle.add(x, y))
# 第二种调用方法
print('Method 2: ', x.add(y))
1
2
3
4
5
6
Method 1:  Tensor(shape=[2, 2], dtype=float64, place=CPUPlace, stop_gradient=True,
       [[6.60000000 , 8.80000000 ],
        [11.        , 13.20000000]])
Method 2:  Tensor(shape=[2, 2], dtype=float64, place=CPUPlace, stop_gradient=True,
       [[6.60000000 , 8.80000000 ],
        [11.        , 13.20000000]])
F（√）1.2.5.1 数学运算

张量类的基础数学函数运算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
x.add(y)                      # 逐元素加
x.subtract(y)                 # 逐元素减
x.multiply(y)                 # 逐元素乘（积）
x.divide(y)                   # 逐元素除
x.mod(y)                      # 逐元素除并取余
x.pow(y)                      # 逐元素幂
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()                       # 指定维度上元素的和，默认为全部维度
F（√）1.2.5.2 逻辑运算

张量类的逻辑运算函数：

1
2
3
4
5
6
7
8
9
x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                # 判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less_than(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近
F（√）1.2.5.3 矩阵运算
1
2
3
4
5
x.t()                         # 矩阵转置
x.transpose([1, 0])           # 交换第 0 维与第 1 维的顺序
x.norm('fro')                 # 矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                # 矩阵（x-y）的2范数
x.matmul(y)                   # 矩阵乘法

有些矩阵运算中也支持大于两维的张量，比如matmul函数，对最后两个维度进行矩阵乘。比如x是形状为[j,k,n,m]的张量，另一个y是[j,k,m,p]的张量，则x.matmul(y)输出的张量形状为[j,k,n,p]。

F（√）1.2.5.4 广播机制

飞桨的一些API在计算时支持广播(Broadcasting)机制，允许在一些运算时使用不同形状的张量。通常来讲，如果有一个形状较小和一个形状较大的张量，会希望多次使用较小的张量来对较大的张量执行某些操作，看起来像是形状较小的张量首先被扩展到和较大的张量形状一致，然后再做运算。

广播机制的条件

飞桨的广播机制主要遵循如下规则（参考Numpy广播机制）：

1）每个张量至少为一维张量。

2）从后往前比较张量的形状，当前维度的大小要么相等，要么其中一个等于1，要么其中一个不存在。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 当两个Tensor的形状一致时，可以广播
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 4))
z = x + y
print('broadcasting with two same shape tensor: ', z.shape)

x = paddle.ones((2, 3, 1, 5))
y = paddle.ones((3, 4, 1))
# 从后往前依次比较：
# 第一次：y的维度大小是1
# 第二次：x的维度大小是1
# 第三次：x和y的维度大小相等，都为3
# 第四次：y的维度不存在
# 所以x和y是可以广播的
z = x + y
print('broadcasting with two different shape tensor:', z.shape)
1
2
broadcasting with two same shape tensor:  [2, 3, 4]
broadcasting with two different shape tensor: [2, 3, 4, 5]

广播机制的计算规则

现在我们知道在什么情况下两个张量是可以广播的。两个张量进行广播后的结果张量的形状计算规则如下：

1）如果两个张量shape的长度不一致，那么需要在较小长度的shape前添加1，直到两个张量的形状长度相等。

2） 保证两个张量形状相等之后，每个维度上的结果维度就是当前维度上较大的那个。

以张量x和y进行广播为例，x的shape为[2, 3, 1，5]，张量y的shape为[3，4，1]。首先张量y的形状长度较小，因此要将该张量形状补齐为[1, 3, 4, 1]，再对两个张量的每一维进行比较。从第一维看，x在一维上的大小为2，y为1，因此，结果张量在第一维的大小为2。以此类推，对每一维进行比较，得到结果张量的形状为[2, 3, 4, 5]。

由于矩阵乘法函数paddle.matmul在深度学习中使用非常多，这里需要特别说明一下它的广播规则：

1）如果两个张量均为一维，则获得点积结果。

2） 如果两个张量都是二维的，则获得矩阵与矩阵的乘积。

3） 如果张量x是一维，y是二维，则将x的shape转换为[1, D]，与y进行矩阵相乘后再删除前置尺寸。

4） 如果张量x是二维，y是一维，则获得矩阵与向量的乘积。

5） 如果两个张量都是N维张量（N > 2），则根据广播规则广播非矩阵维度（除最后两个维度外其余维度）。比如：如果输入x是形状为[j,1,n,m]的张量，另一个y是[k,m,p]的张量，则输出张量的形状为[j,k,n,p]。

矩阵乘法示例

1
2
3
4
x = paddle.ones([10, 1, 5, 2])
y = paddle.ones([3, 2, 5])
z = paddle.matmul(x, y)
print('After matmul: ', z.shape)
1
After matmul:  [10, 3, 5, 5]

笔记
飞桨的API有原位（inplace）操作和非原位操作之分。原位操作即在原张量上保存操作结果，非原位操作则不会修改原张量，而是返回一个新的张量来表示运算结果。在飞桨框架V2.1及之后版本，部分API有对应的原位操作版本，在API后加上’_‘表示，如：x.add(y)是非原位操作，x.add_(y)为原位操作。

D（√）1.3 算子

一个复杂的机器学习模型（比如神经网络）可以看作一个复合函数，输入是数据特征，输出是标签的值或概率。简单起见，假设一个由$L$个函数复合的神经网络定义为：
$$
y=f_L(\cdots f_2(f_1(x))),
$$

其中$f_l(\cdot)$可以为带参数的函数，也可以为不带参数的函数，$x$为输入特征，$y$为某种损失。
我们将从$x$到$y$的计算看作一个前向计算过程。而神经网络的参数学习需要计算损失关于所有参数的偏导数（即梯度）。假设函数$f_l(\cdot)$包含参数$\theta_l$，根据链式法则，

$$
\begin{aligned}
\frac{\partial y}{\partial \theta_l} &= {\frac{\partial f_l}{\partial \theta_l}} \frac{\partial y}{\partial f_l} \
&= \frac{\partial f_l}{\partial \theta_l} \frac{\partial f_{l+1}}{\partial f_l} \cdots \frac{\partial f_L}{\partial f_{L-1}} .
\end{aligned}
$$

在实践中，一种比较高效的计算$y$关于每个函数$f_l$的偏导数的方式是利用递归进行反向计算。令$\delta_l\triangleq \frac{\partial y}{\partial f_l}$，则有
$$
\delta_{l-1} = \frac{\partial f_l}{\partial f_{l-1}} \delta_{l}.
$$

如果将函数$f_l(\cdot)$称为前向函数，则$\delta_{l-1}$的计算称为函数$f(x)$的反向函数。

如果我们实现每个基础函数的前向函数和反向函数，就可以非常方便地通过这些基础函数组合出复杂函数，并通过链式法则反向计算复杂函数的偏导数。
在深度学习框架中，这些基本函数的实现称为算子(Operator，Op)。有了算子，就可以像搭积木一样构建复杂的模型。

E（√）1.3.1 算子定义

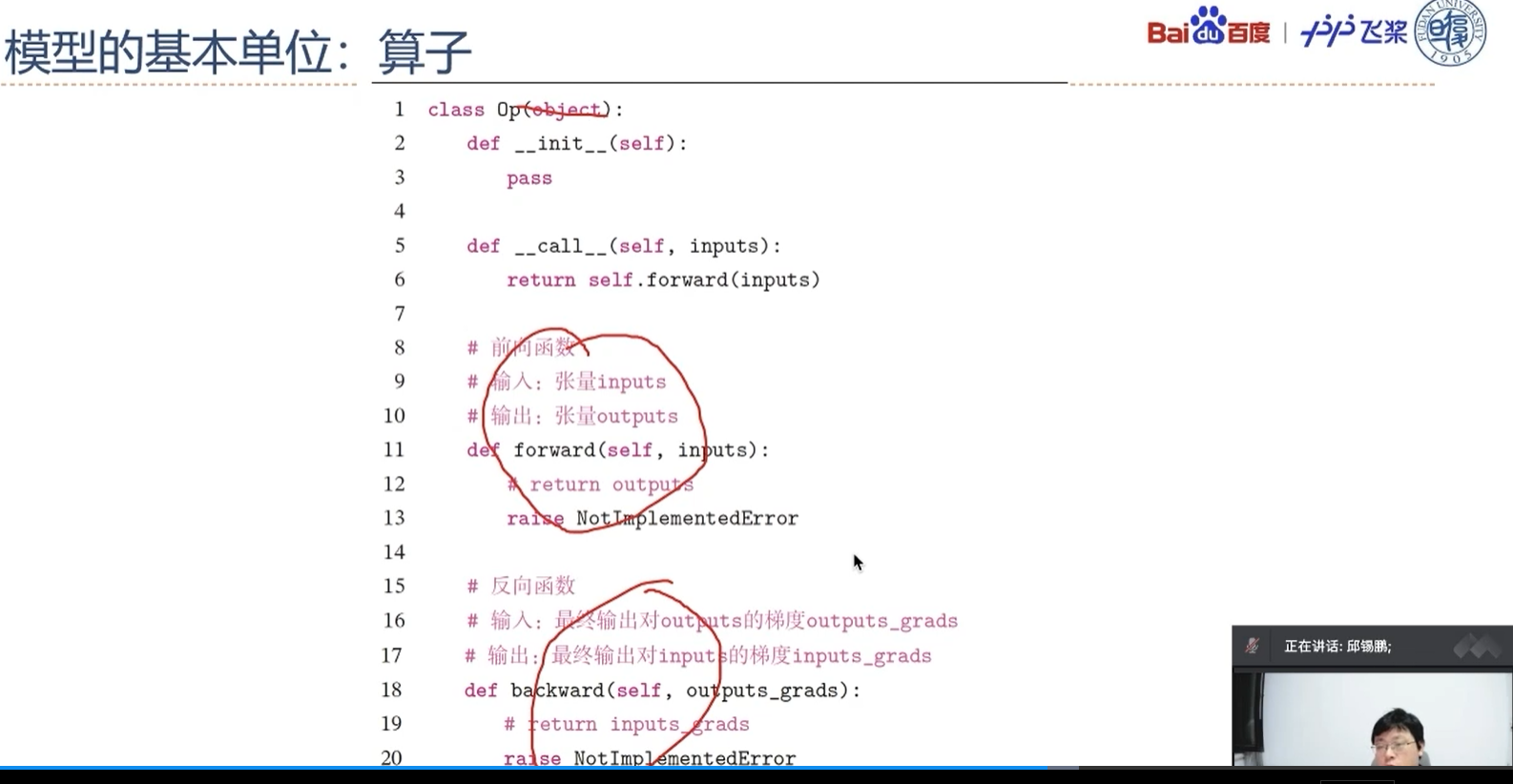
算子是构建复杂机器学习模型的基础组件，包含一个函数f(x)f(x)f(x)的前向函数和反向函数。为了可以更便捷地进行算子组合，本书中定义算子Op}的接口如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    # 前向函数
    # 输入：张量inputs
    # 输出：张量outputs
    def forward(self, inputs):
        # return outputs
        raise NotImplementedError

    # 反向函数
    # 输入：最终输出对outputs的梯度outputs_grads
    # 输出：最终输出对inputs的梯度inputs_grads
    def backward(self, outputs_grads):
        # return inputs_grads
        raise NotImplementedError

在上面的接口中，forward是自定义Op的前向函数，必须被子类重写，它的参数为输入对象，参数的类型和数量任意；backward是自定义Op的反向函数，必须被子类重写，它的参数为forward输出张量的梯度outputs_grads，它的输出为forward输入张量的梯度inputs_grads。

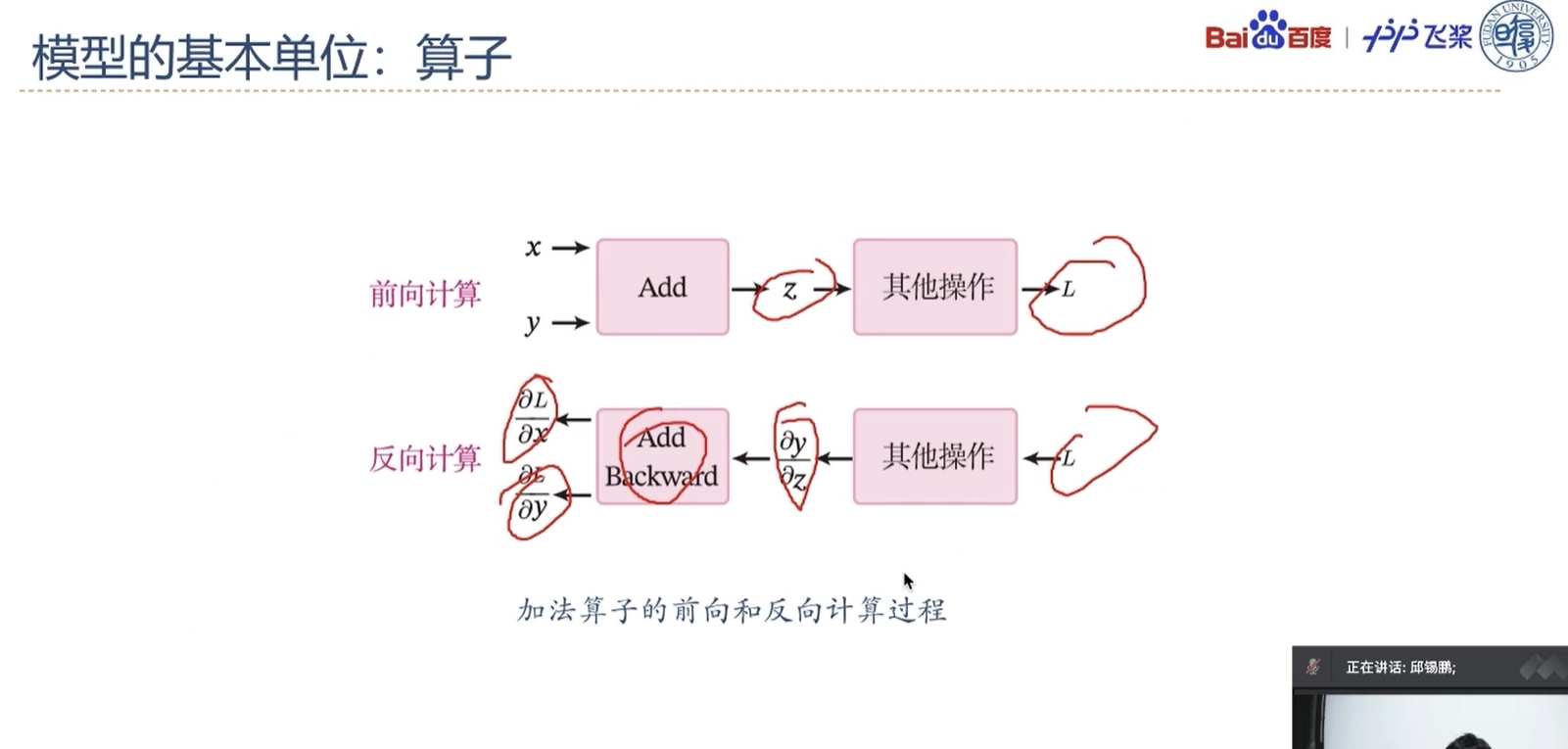
F（√）1.3.1.1 加法算子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class add(Op):
    def __init__(self):
        super(add, self).__init__()

    def __call__(self, x, y):
        return self.forward(x, y)

    def forward(self, x, y):
        self.x = x
        self.y = y
        outputs = x + y
        return outputs

    def backward(self, grads):
        grads_x = grads * 1
        grads_y = grads * 1
        return grads_x, grads_y

定义x=1、y=4，根据反向计算，得到x、y的梯度。

1
2
3
4
5
6
7
x = 1
y = 4
add_op = add()
z = add_op(x, y)
grads_x, grads_y = add_op.backward(grads=1)
print("x's grad is: ", grads_x)
print("y's grad is: ", grads_y)
1
2
x's grad is:  1
y's grad is:  1
F（√）1.3.1.2 乘法算子

乘法算子的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class multiply(Op):
    def __init__(self):
        super(multiply, self).__init__()

    def __call__(self, x, y):
        return self.forward(x, y)

    def forward(self, x, y):
        self.x = x
        self.y = y
        outputs = x * y
        return outputs

    def backward(self, grads):
        grads_x = grads * self.y
        grads_y = grads * self.x
        return grads_x, grads_y
F（√）1.3.1.3 指数算子

指数算子的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import math

class exponential(Op):
    def __init__(self):
        super(exponential, self).__init__()

    def forward(self, x):
        self.x = x
        outputs = math.exp(x)
        return outputs

    def backward(self, grads):
        grads = grads * math.exp(self.x)
        return grads

分别指定a、b、c、d的值，通过实例化算子，调用加法、乘法和指数运算算子，计算得到y。

1
2
3
4
5
6
7
a, b, c, d = 2, 3, 2, 2
# 实例化算子
multiply_op = multiply()
add_op = add()
exp_op = exponential()
y = exp_op(add_op(multiply_op(a, b), multiply_op(c, d)))
print('y: ', y)
1
22026.465794806718
E（√）1.3.2 自动微分机制

目前大部分深度学习平台都支持自动微分（Automatic Differentiation），即根据forward()函数来自动构建backward()函数。

笔记

自动微分的原理是将所有的数值计算都分解为基本的原子操作，并构建\mykey{计算图}{Computational Graph}。计算图上每个节点都是一个原子操作，保留前向和反向的计算结果，很方便通过链式法则来计算梯度。自动微分的详细介绍可以参考《神经网络与深度学习》第4.5节。

飞桨的自动微分是通过trace的方式，记录各种算子和张量的前向计算，并自动创建相应的反向函数和反向变量，来实现反向梯度的计算。

在飞桨中，可以通过paddle.grad()API或张量类成员函数x.grad来查看张量的梯度。

下面用一个比较简单的例子来了解整个过程。定义两个张量a和b，并用stop_gradient属性用来设置是否传递梯度。将a的stop_gradient属性设为False，会自动为a创建一个反向张量，将b的stop_gradient属性设为True，即不会为b创建反向张量。

1
2
3
4
5
6
7
8
9
10
# 定义张量a，stop_gradient=False代表进行梯度传导
a = paddle.to_tensor(2.0, stop_gradient=False)
# 定义张量b，stop_gradient=True代表不进行梯度传导
b = paddle.to_tensor(5.0, stop_gradient=True)
c = a * b
# 自动计算反向梯度
c.backward()
print("Tensor a's grad is: {}".format(a.grad))
print("Tensor b's grad is: {}".format(b.grad))
print("Tensor c's grad is: {}".format(c.grad))
1
2
3
4
5
Tensor a's grad is: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [5.]) # a的梯度是b
Tensor b's grad is: None # b关闭了梯度，因此没有梯度
Tensor c's grad is: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
       [1.]) # c的梯度是1
F（√）1.3.2.1 前向执行

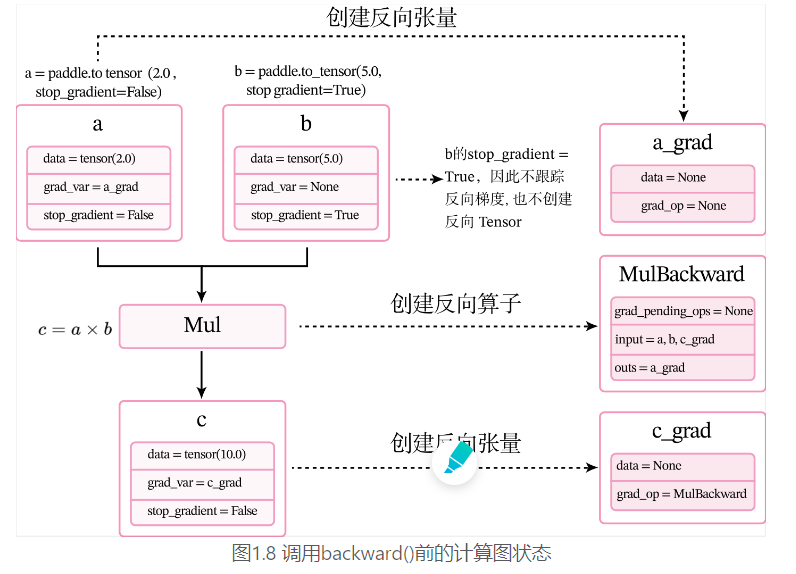
在上面代码中，第7行c.backward()被执行前，会为每个张量和算子创建相应的反向张量和反向函数。

当创建张量或执行算子的前向计算时，会自动创建反向张量或反向算子。这里以上面代码中乘法为例来进行说明。

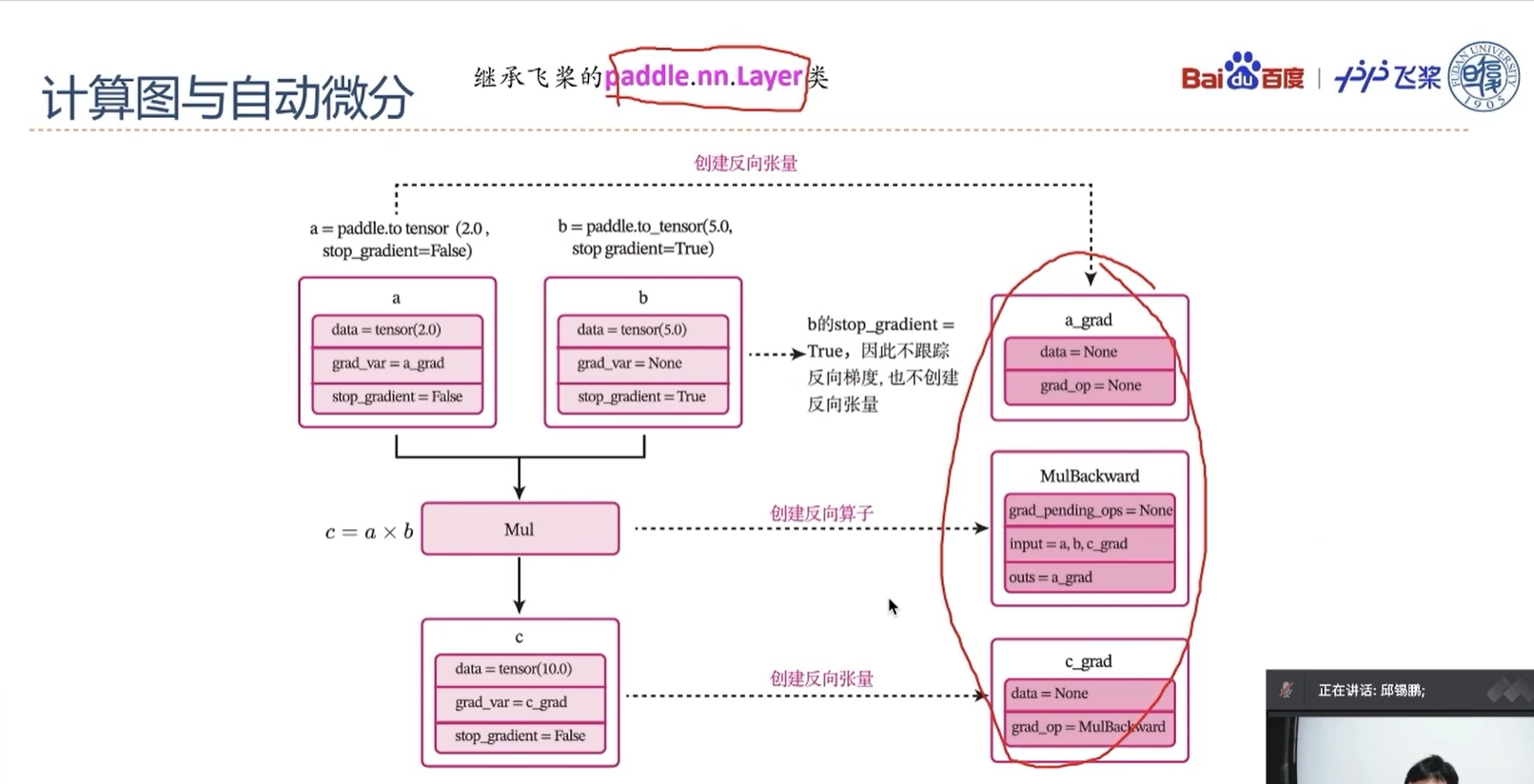
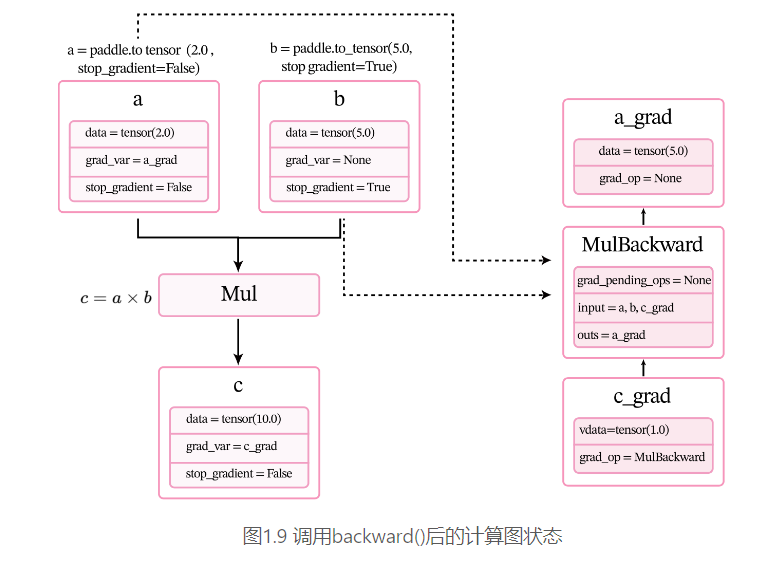
  1. 当创建张量a时，由于其属性stop_gradient=False，因此会自动为a创建一个反向张量，也就是图1.8中的a_grad。由于a不依赖其它张量或算子，a_grad的grad_op为None。
  2. 当创建张量b时，由于其属性stop_gradient=True，因此不会为b创建一个反向张量。
  3. 执行乘法c=a×bc=a\times bc=a×b 时，×\times×是一个前向算子Mul，为其构建反向算子MulBackward。由于Mul的输入是a和b，输出是c，对应反向算子MulBackward的输入是张量c的反向张量c_grad，输出是a和b的反向张量。如果输入定义stop_gradient=True，反向张量即为None。在此例子中就是a_grad和None。
  4. 反向算子MulBackward中的grad_pending_ops用于在自动构建反向网络时，明确该反向算子的下一个可执行的反向算子。可以理解为在反向计算中，该算子衔接的下一个反向算子。
  5. 当c通过乘法算子Mul被创建后，c会创建一个反向张量c_grad，它的grad_op为该乘法算子的反向算子，即MulBackward。

由于此时还没有进行反向计算，因此这些反向张量和反向算子中的具体数值为空(data = None)。

image-20221211203408158

F（√）1.3.2.2 反向执行

调用backward()后，执行计算图上的反向过程，即通过链式法则自动计算每个张量或算子的微分，计算过程如图1.9所示。经过自动反向梯度计算，获得c_grad和a_grad的值。

image-20221211203606088

E（√）1.3.3 预定义的算子

从零开始构建各种复杂的算子和模型是一个很复杂的过程，在开发的过程中也难以避免地会出现很多冗余代码，因此飞桨提供了基础算子和中间算子，可以便捷地实现复杂模型。

在深度学习中，大多数模型都是以各种神经网络为主，由一系列层(Layer)组成，层是模型的基础逻辑执行单元。飞桨提供了paddle.nn.Layer类来方便快速地实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。

当我们实现的算子继承paddle.nn.Layer类时，就不用再定义backward函数。飞桨的自动微分机制可以自动完成反向传播过程，让我们只关注模型构建的前向过程，不必再进行烦琐的梯度求导。

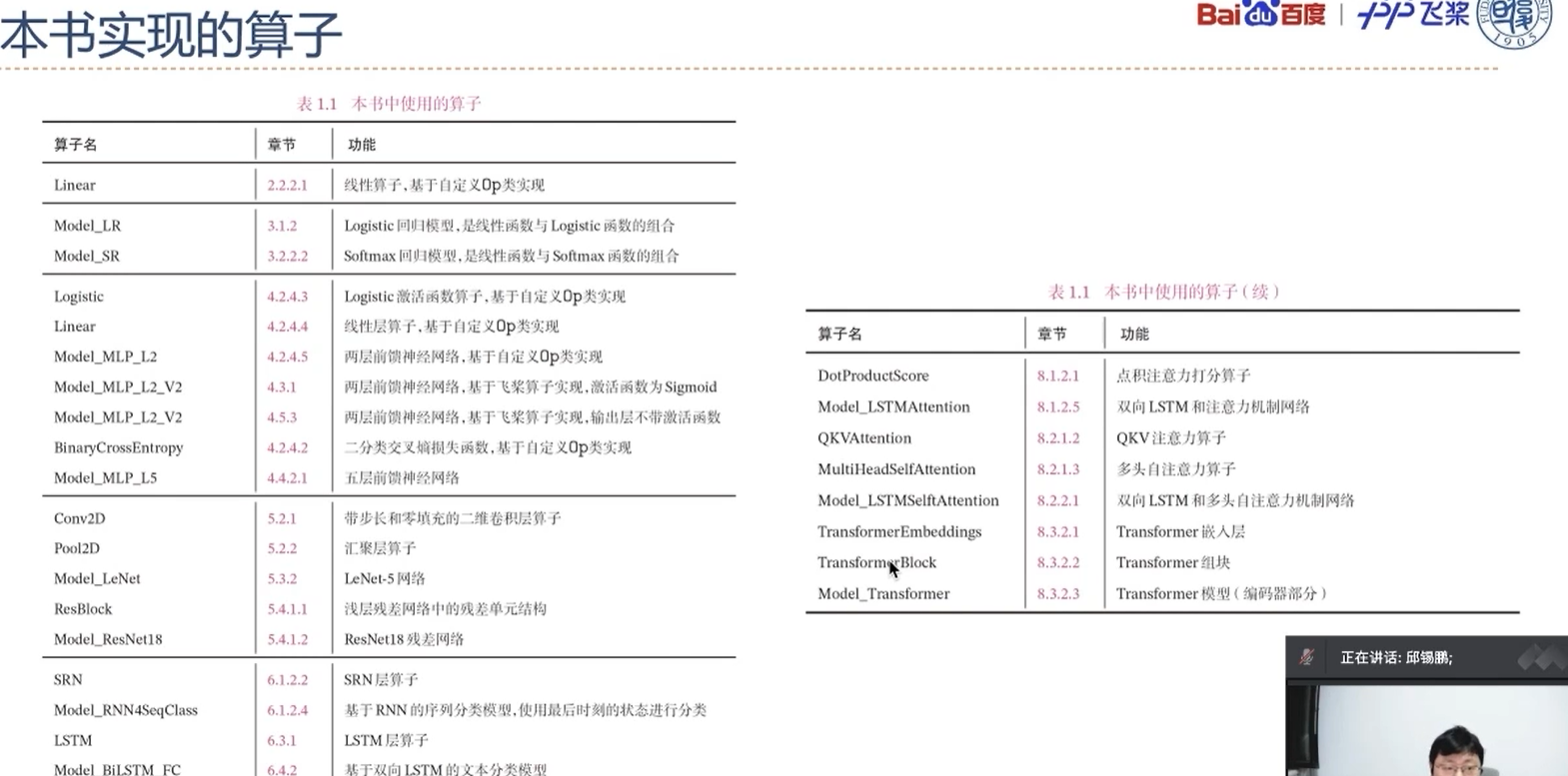
E（√）1.3.4 本书中实现的算子

更深入的理解深度学习的模型和算法，在本书中，我们也手动实现自己的算子库：nndl，并基于自己的算子库来构建机器学习模型。本书中的自定义算子分为两类：一类是继承在第1.3.1节中定义Op类，这些算子是为了进行更好的展示模型的实现细节，需要自己动手计算并实现其反向函数；另一类是继承飞桨的paddle.nn.Layer类，更方便地搭建复杂算子，并和飞桨预定义算子混合使用。

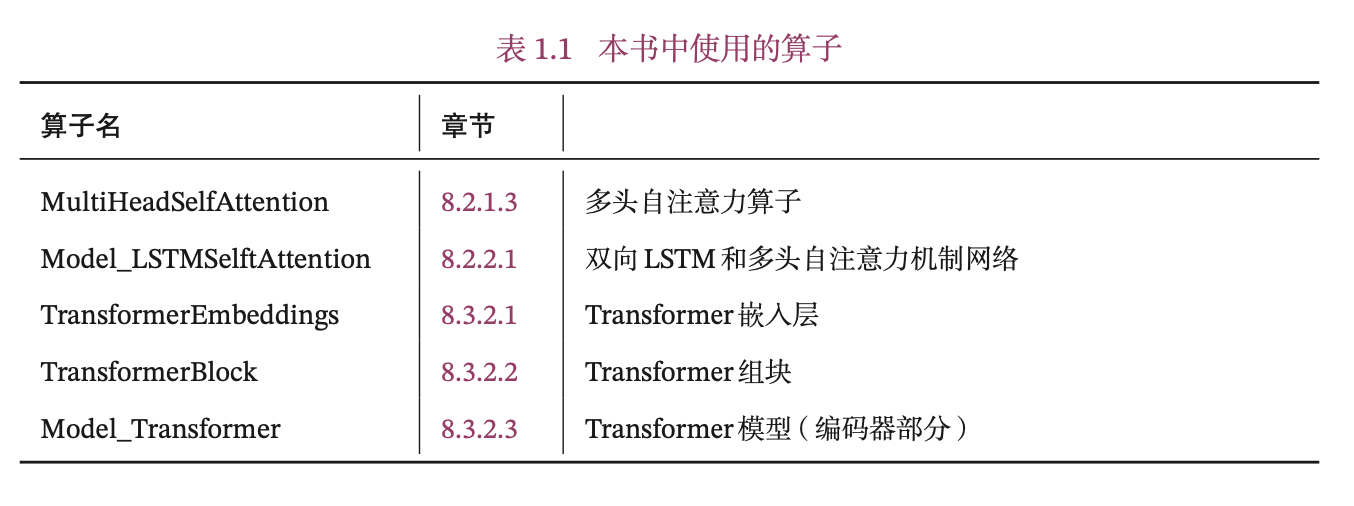
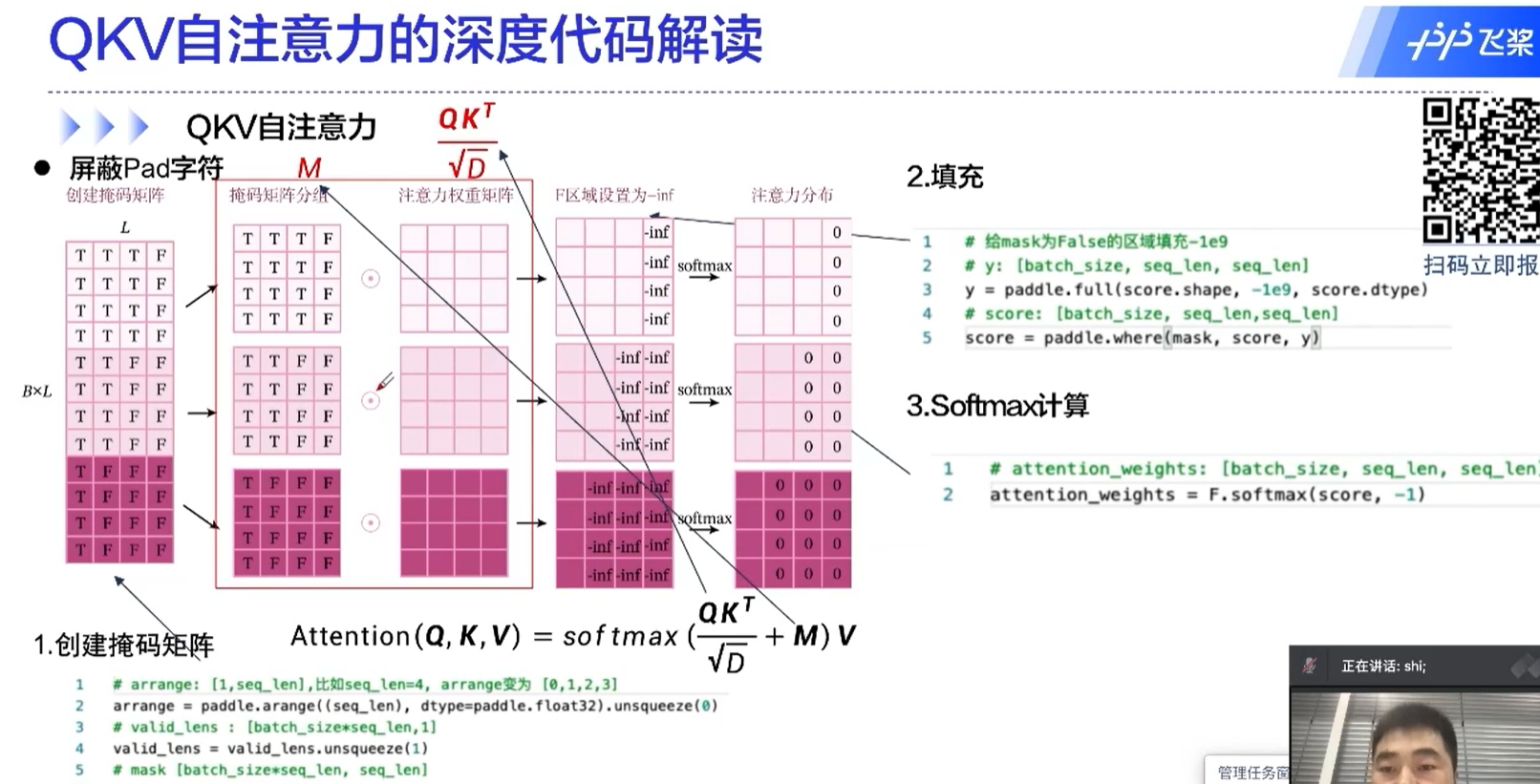
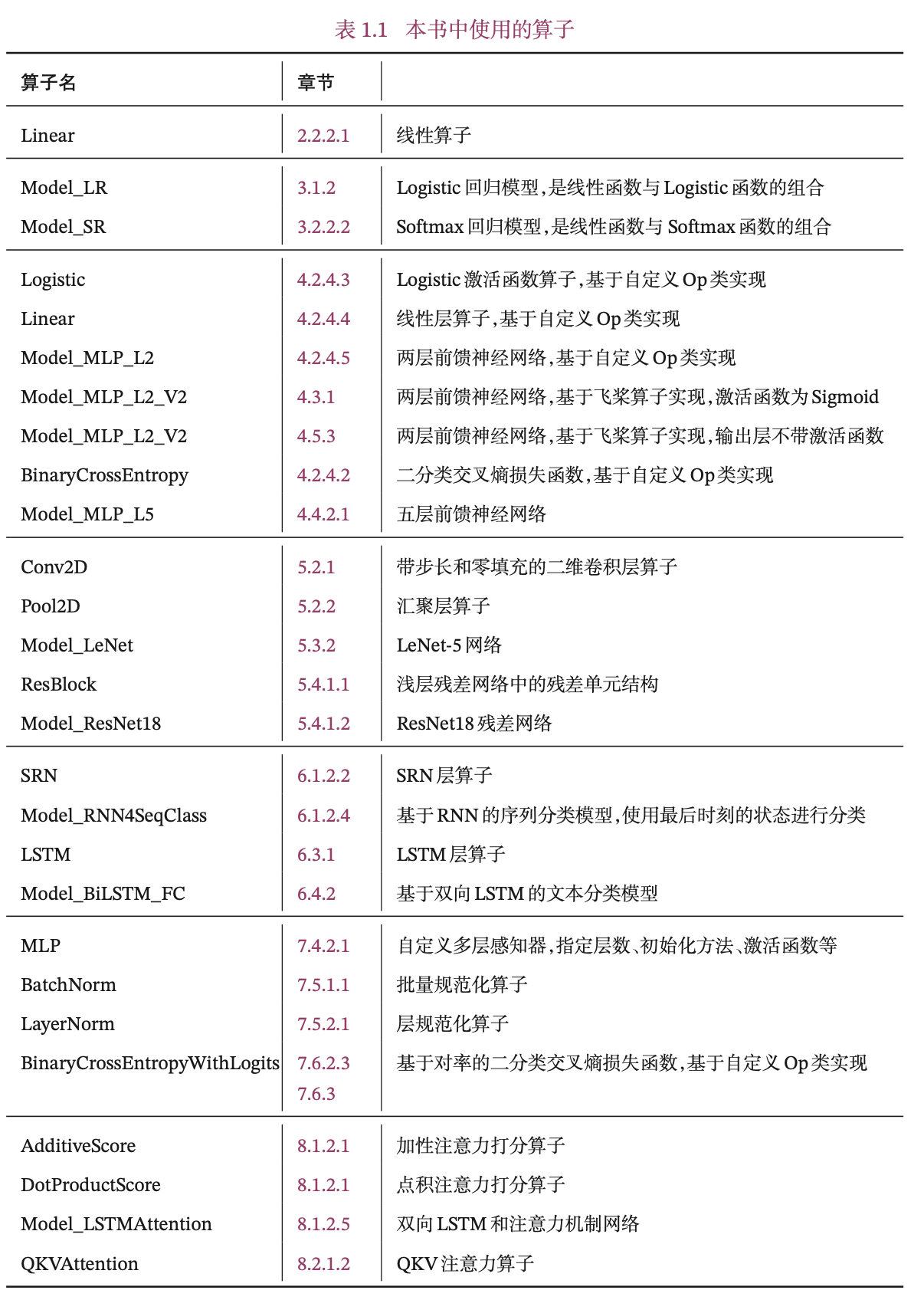
本书中实现的算子见表1.1所示，其中Model_开头为完整的模型。

img

img

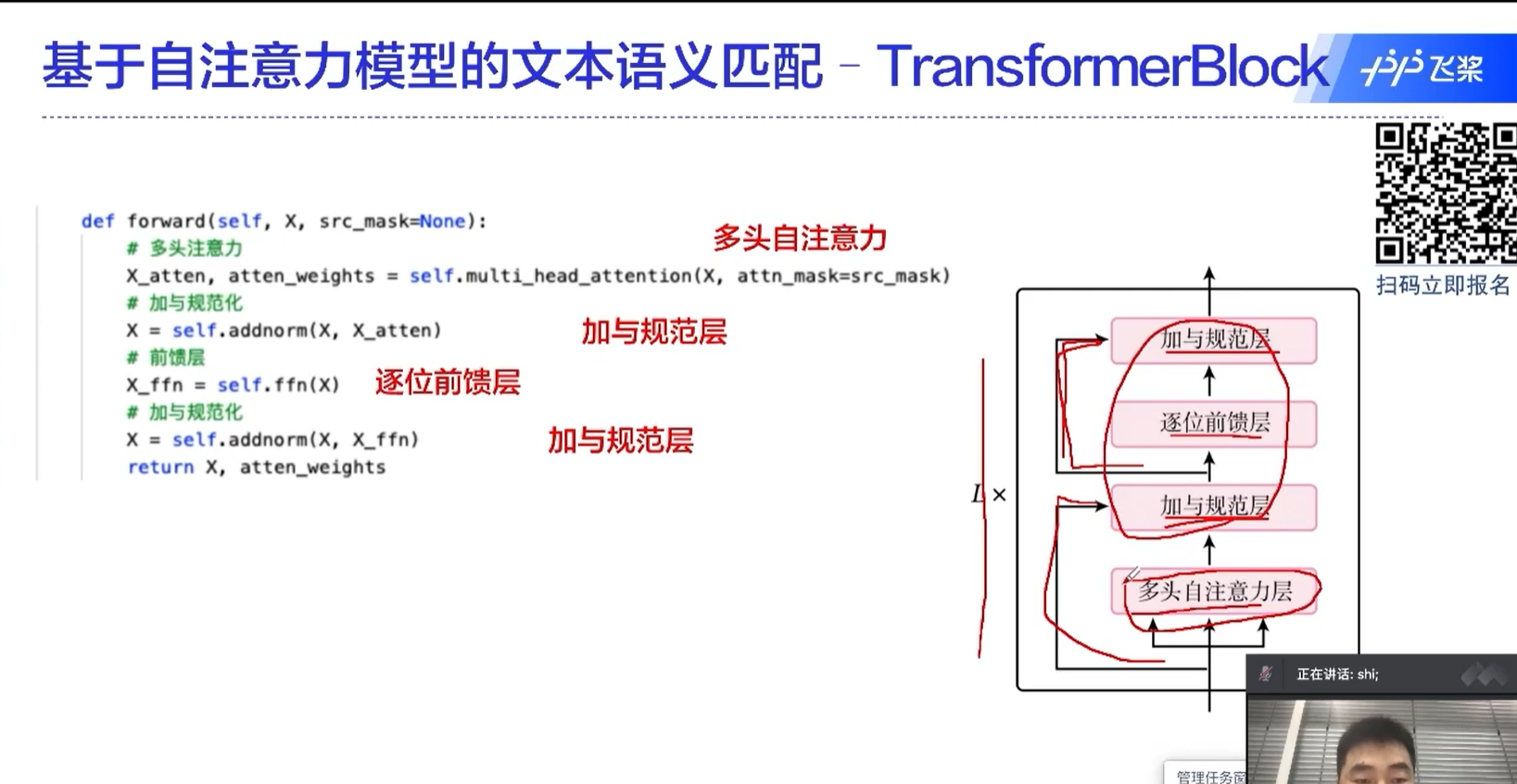
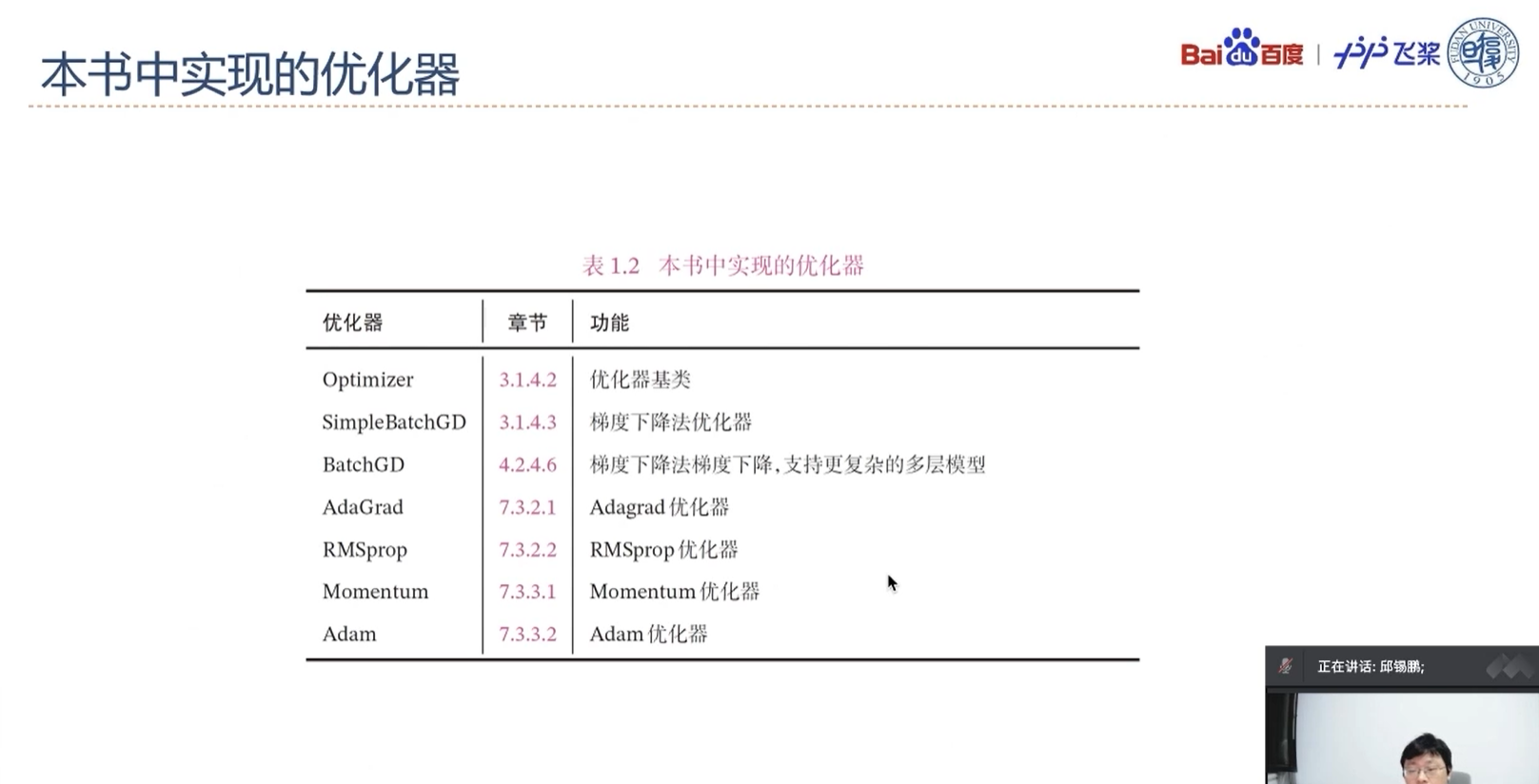
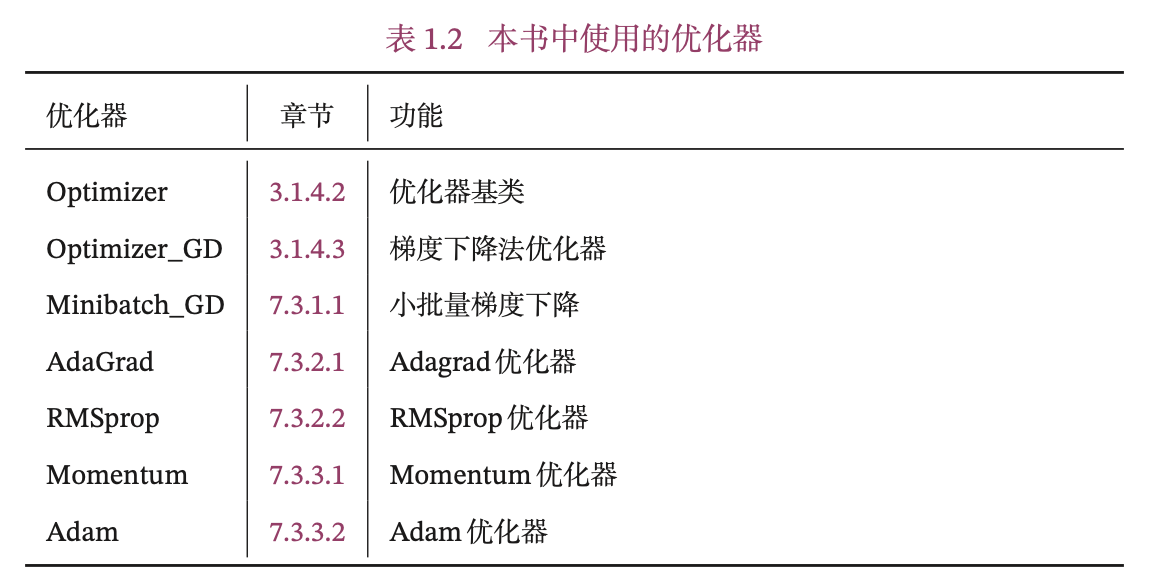
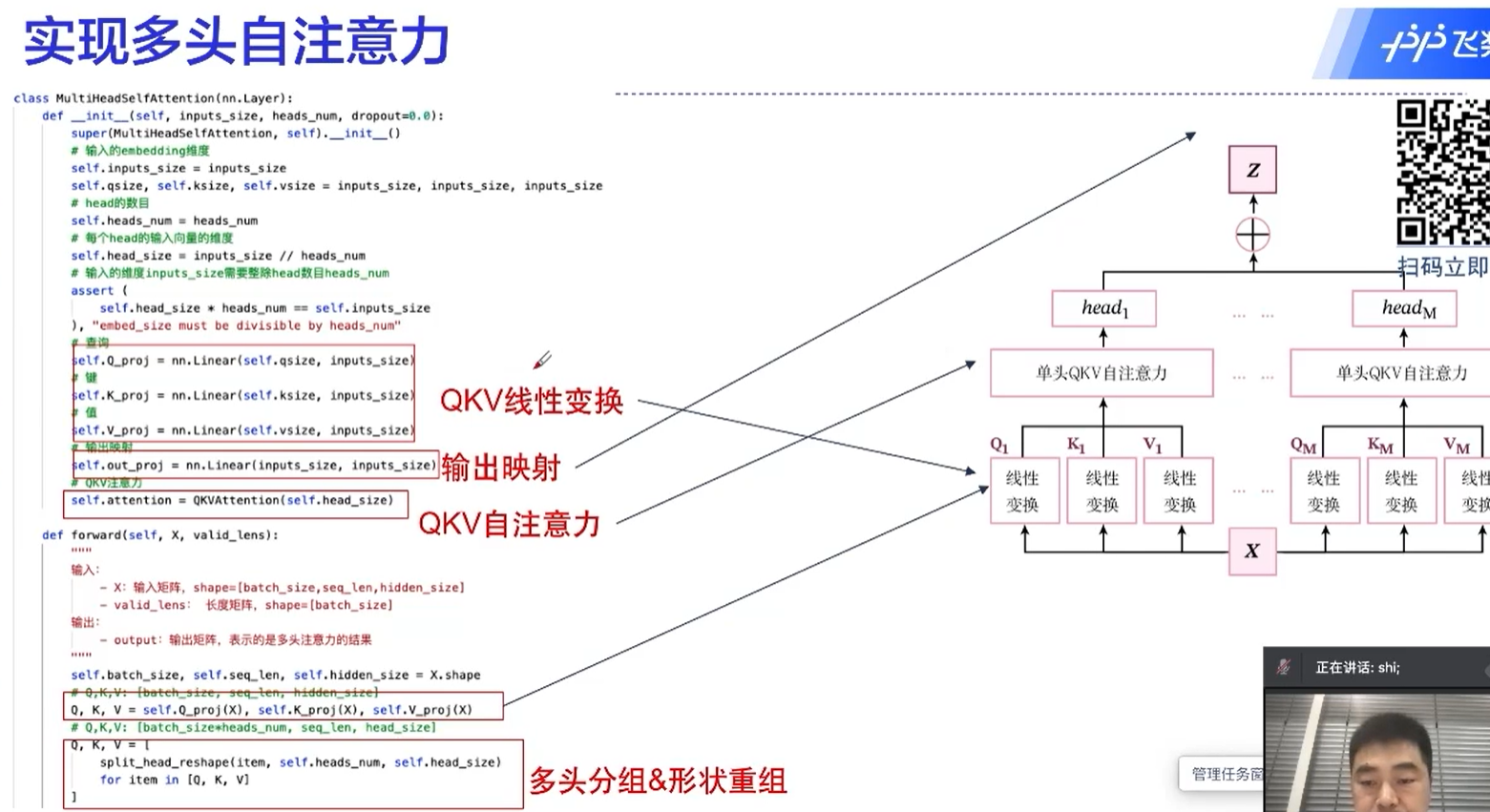
E（√）1.3.6 本书中实现的优化器

img

D（√）1.4 本书中实现的DataSet类

为了更好地实践，本书在模型解读部分主要使用简单任务和数据集，在案例实践部分主要使用公开的实际案例数据集。下面介绍我们用到的数据集以及对应构建的DataSet类。

E（√）1.4.1 数据集

本书中使用的数据集如下：

  1. 线性回归数据集ToyLinear150：在第2.2.1.2节中构建，用于简单的线性回归任务。ToyLinear150数据集包含150条带噪音的样本数据，其中训练集100条、测试集50条，由在第2.2.1.2节中create_toy_data函数构建。
  2. 非线性回归数据集ToySin25：在第2.3.1节中构建，用于简单的多项式回归任务.ToySin25数据集包含25条样本数据，其中训练集15条、测试集10条。ToySin25数据集同样使用在第2.2.1.1节中create_toy_data函数进行构建。
  3. 波士顿房价预测数据集：波士顿房价预测数据集共506条样本数据，每条样本包含了12种可能影响房价的因素和该类房屋价格的中位数。该数据集在第2.5节中使用。
  4. 二分类数据集Moon1000：在第3.1中构建，二分类数据集Moon1000数据是从两个带噪音 的弯月形状数据分布中采样得到，每个样本包含2个特征，其中训练集640条、验证集160条、测试集200条。该数据集在本书第3.1节和第4.2节中使用。数据集构建函数make_moons在第7.4.2.3节和第7.6节中使用。
  5. 三分类数据集Multi1000：在第3.2.1节中构建三分类数据集集Multi1000，其中训练集640条、验证集160条、测试集200条。该数据集来自三个不同的簇，每个簇对应一个类别。
  6. 鸢尾花数据集：鸢尾花数据集包含了3种鸢尾花类别(Setosa、Versicolour、Virginica)，每种类别有50个样本，共计150个样本。每个样本中包含了4个属性：花萼长度、花萼宽度、花瓣长度以及花瓣宽度。该数据集在第3.3节和第4.5节使用。
  7. MNIST数据集：MNIST手写数字识别数据集是计算机视觉领域的经典入门数据集，包含了训练集60 000条、测试集10 000条。MNIST数据集在第5.3.1节和第7.2节中使用。
  8. CIFAR-10 数据集：CIFAR-10数据集是计算机视觉领域的经典数据集，包含了10种不同的类别、共 60 000 张图像，其中每个类别的图像都是6 000 张，图像大小均为32×32像素。CIFAR-10数据集在第5.5节中使用.
  9. IMDB电影评论数据集：IMDB电影评论数据集是一份关于电影评论的经典二分类数据集。IMDB按照评分的高低筛选出了积极评论和消极评论，如果评分≥7，则认为是积极评论；如果评分≤4，则认为是消极评论。数据集包含训练集和测试集数据，数量各为25 000 条，每条数据都是一段用户关于某个电影的真实评价，以及观众对这个电影的情感倾向。IMDB数据集在第6.4节、第8.1节和第8.2节中使用.
  10. 数字求和数据集DigitSum：在第6.1.1节中构建，包含用于数字求和任务的不同长度的数据集。数字求和任务的输入是一串数字，前两个位置的数字为0-9，其余数字随机生成(主要为0)，预测目标是输入序列中前两个数字的加和，用来测试模型的对序列数据的记忆能力。
  11. LCQMC通用领域问题匹配数据集：LCQMC数据集是百度知道领域的中文问题匹配数据集，目的是为了解决在中文领域大规模问题匹配数据集的缺失。该数据集从百度知道不同领域的用户问题中抽取构建数据。LCQMC数据集共包含训练集238 766条、验证集8 802条和测试集12 500 条。LCQMC数据集在第8.3节中使用。
E（√）1.4.2 Dataset类

为了更好地支持使用随机梯度下降进行参数学习，我们构建了DataSet类，以便可以更好地进行数据迭代。

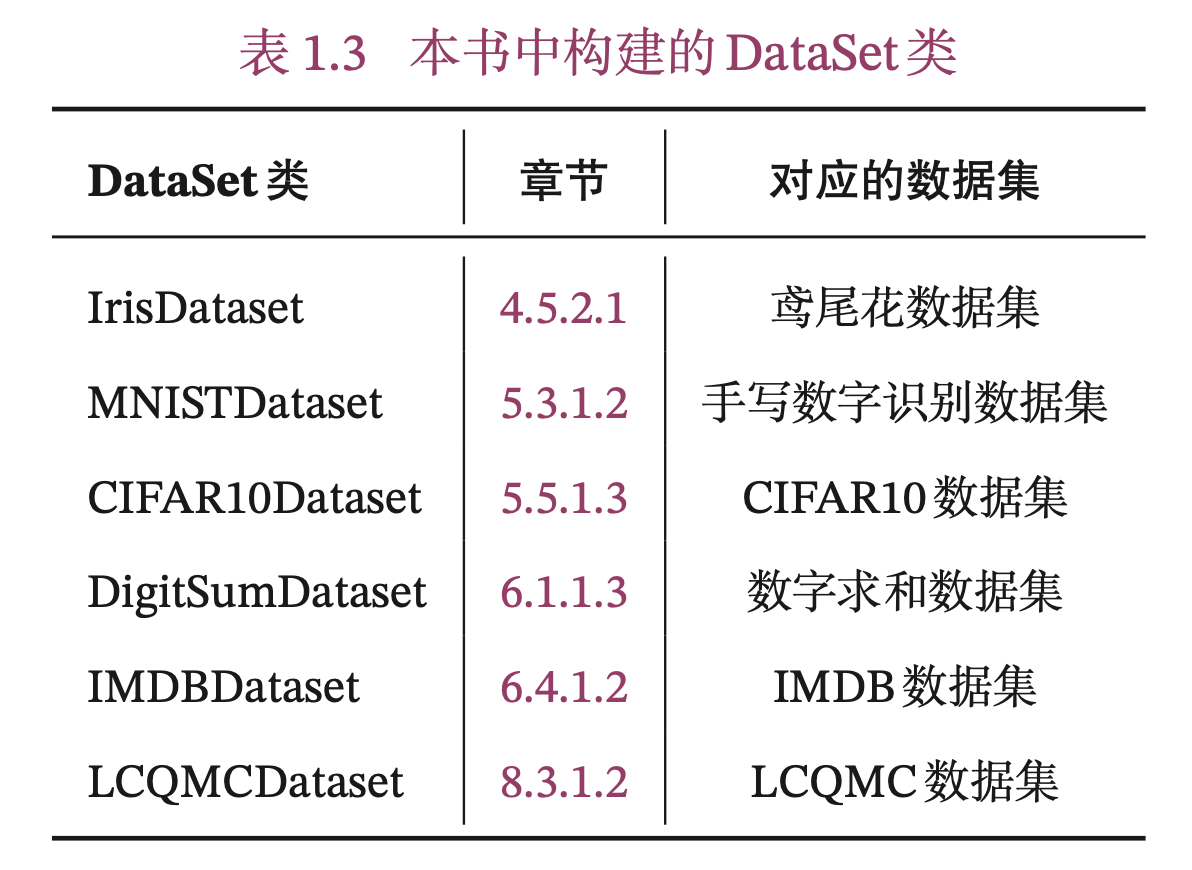
本书中构建的DataSet类见表1.3。关于Dataset类的具体介绍见第4.5.1.1节。

img

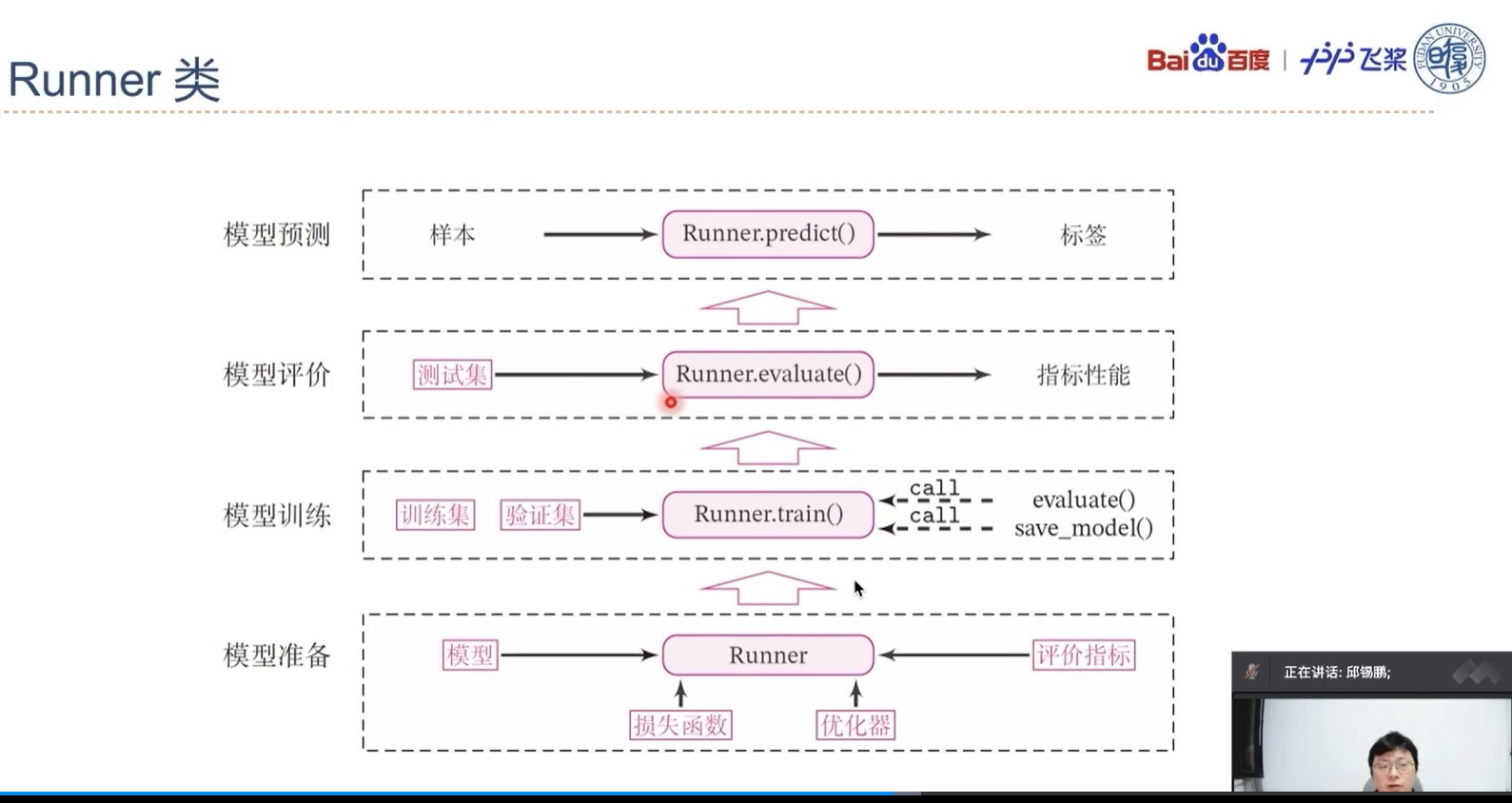
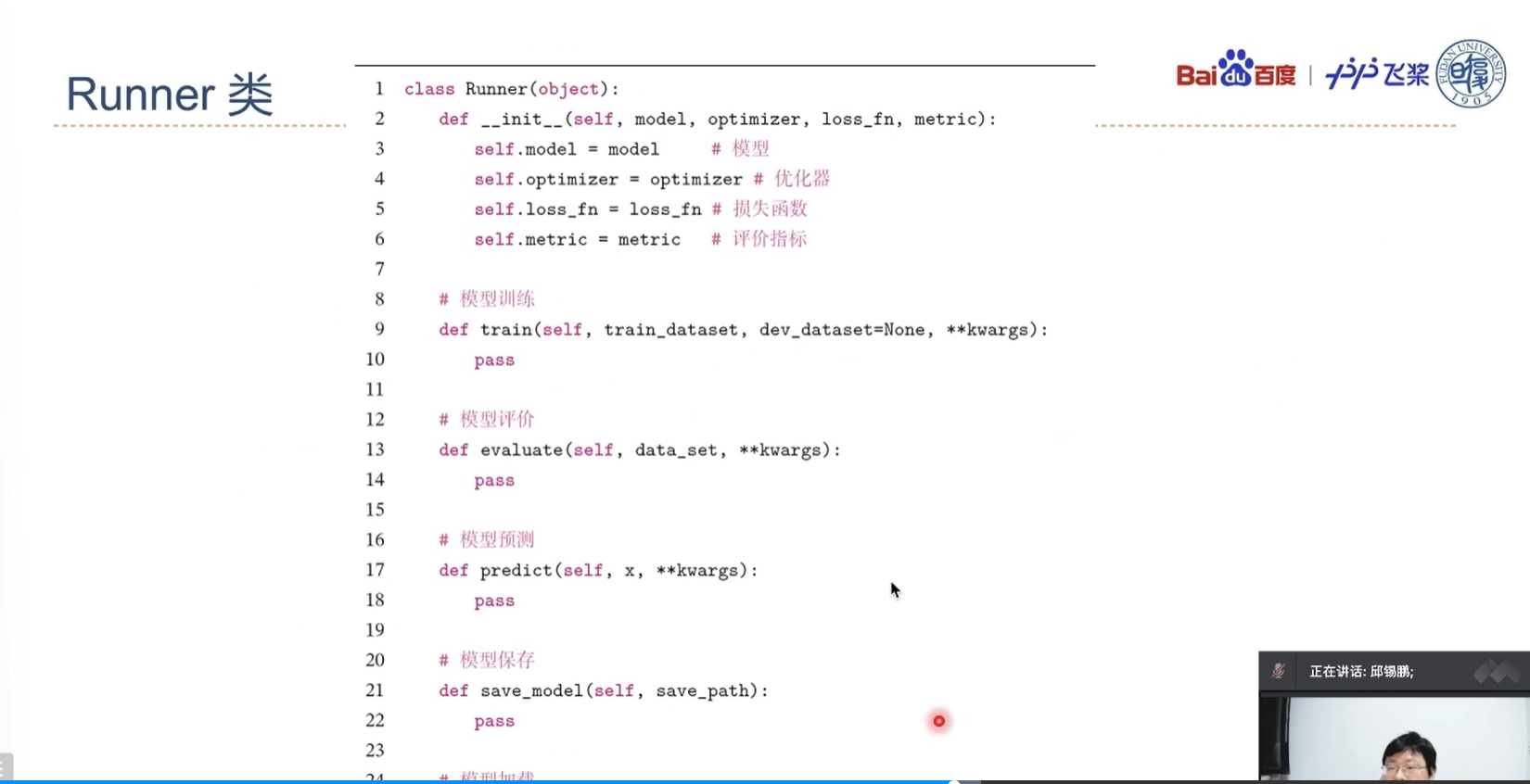
D（√）1.5 本书中使用的Runner类

在一个任务上应用机器学习方法的流程基本上包括：数据集构建、模型构建、损失函数定义、优化器定义、评价指标定义、模型训练、模型评价和模型预测等环节。为了将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类，使得我们可以更方便进行机器学习实践。除上述提到的要素外，Runner类还包括模型保存、模型加载等功能。Runner类的具体介绍可参见第2节. 这里我们对本书中用到的三个版本的Runner类进行汇总，说明每一个版本Runner类的构成方式.

  1. RunnerV1：在第2节中实现，用于线性回归模型的训练，其中训练过程通过直接求解解析解的方式得到模型参数，没有模型优化及计算损失函数过程，模型训练结束后保存模型参数。
  2. RunnerV2：在第3.1.6节中实现。RunnerV2主要增加的功能为：
  • 在训练过程引入梯度下降法进行模型优化；
  • 模型训练过程中计算在训练集和验证集上的损失及评价指标并打印，训练过程中保存最优模型。我们在第4.3.2节和第4.3.2节分别对RunnerV2进行了完善，加入自定义日志输出、模型阶段控制等功能。
  1. RunnerV3：在第4.5.4节中实现。RunnerV3主要增加三个功能：使用随机梯度下降法进行参数优化；训练过程使用DataLoader加载批量数据；模型加载与保存中，模型参数使用state_dict方法获取，使用state_dict加载。

D（√）1.6 小结

深度学习技术栈 > 深度学习 > 实践学习 > 神经网络与深度学习：案例与实践 - 飞桨 - 邱锡鹏
第1章 - 实践基础1
https://alec-97.github.io/posts/2304768005/
作者
Shuai Zhao
发布于
2022年11月20日
许可协议