4 - 前馈神经网络
本文最后更新于:3 个月前
[√] 4 - 课节4:前馈神经网络
[√] 4.0 - 前馈神经网络概述
本节讲非线性的分类器,这个分类器主要就是神经网络。今天讲的第一种神经网络是前馈神经网络。

[√] 4.1 - 神经元
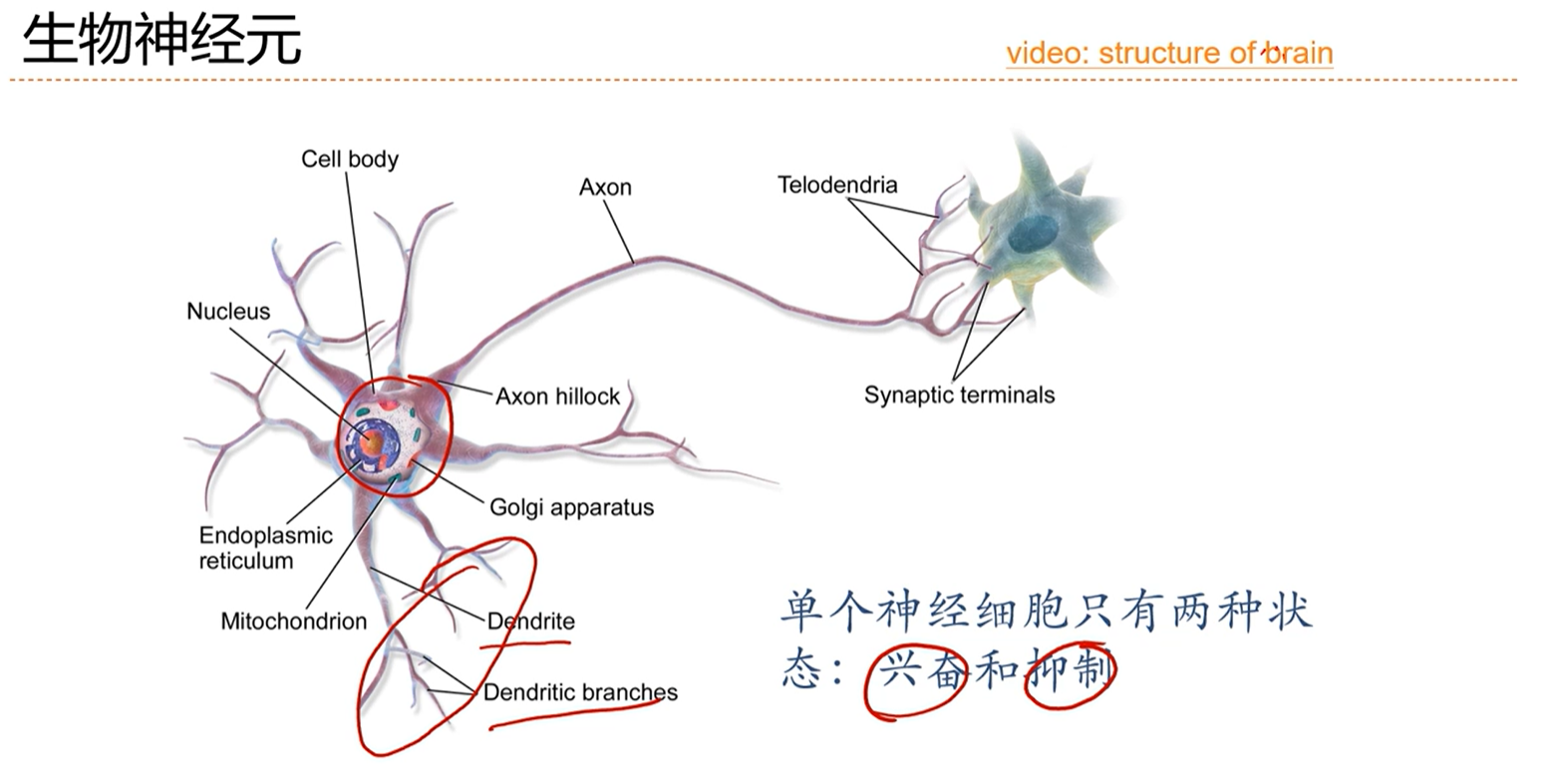
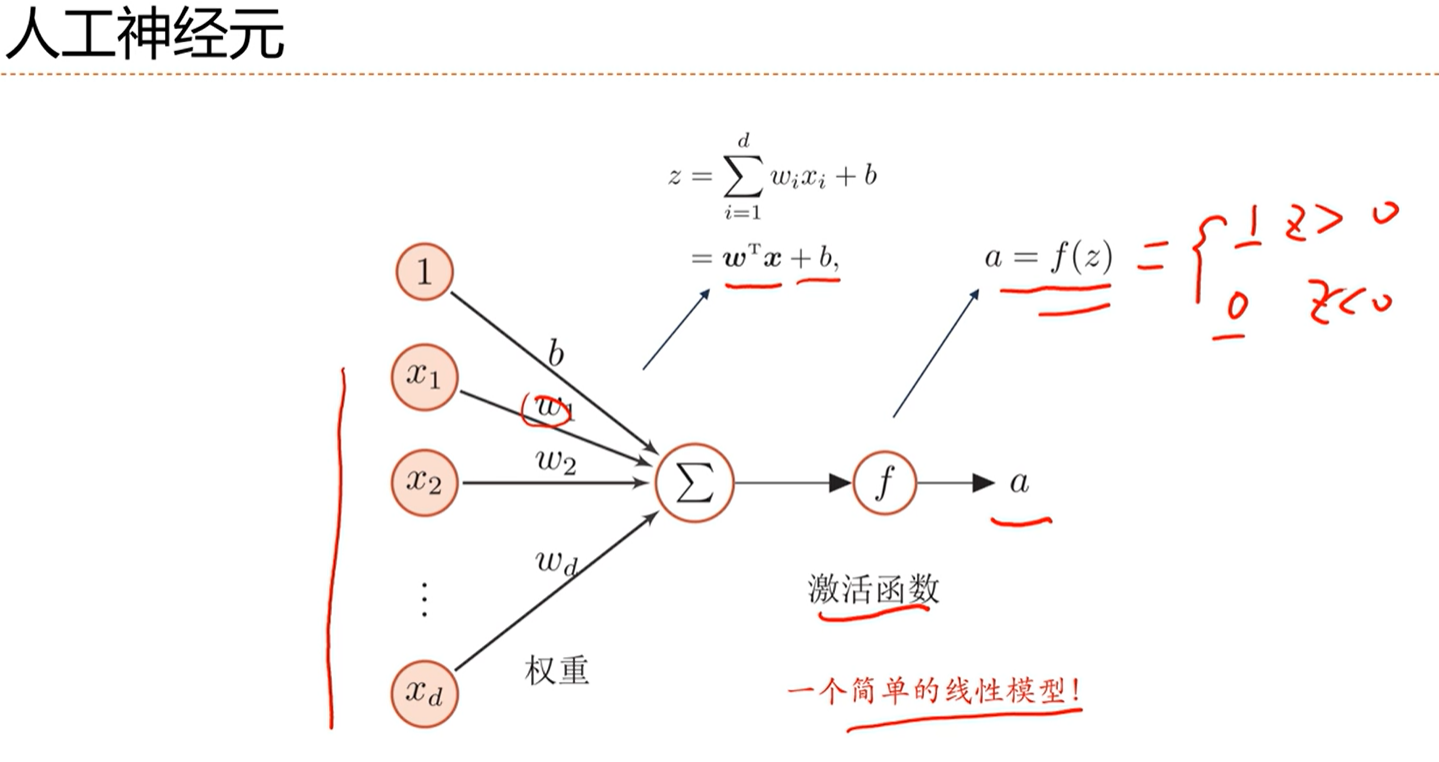

偏置b的作用是:调节阈值,即达到什么程度就兴奋。
这个人工神经元可以看做是一个简单的线性模型。
这个神经元可以看做两部分,前半部分看做是收集信息,后半部分看做是一个非线性函数,用来将收集的信息映射到一个激活的状态上。
不同类型的神经元主要的区别其实就是在于激活函数怎么设计。
通常来讲a的取值范围是一个比z的取值范围更小的区域。
三种常用的激活函数
- s型函数(sigmoid function):比如sigmoid激活函数、logistic函数、tanh函数等
- 斜坡函数(ramp function):ReLU、leaky ReLU、ELU等
- 复合函数:既带有s型函数的性质、又带有斜坡函数的性质
S型函数
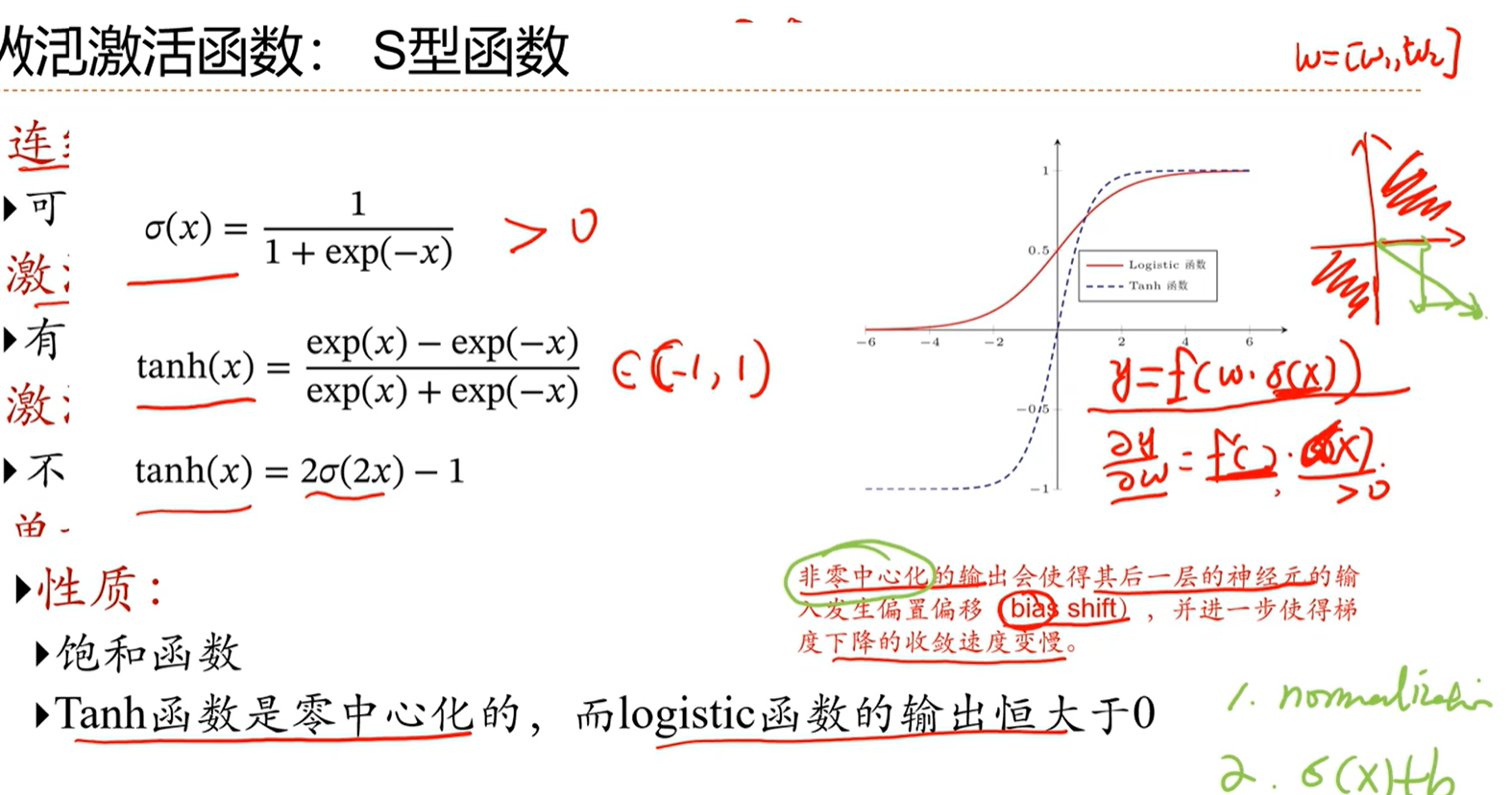
比如logistic函数,值在0-1之间,模拟神经元的两种状态
tanh函数和logistic函数能够相互转换,因此这两种函数的能力基本上是等价的
tanh函数的能力比logistic函数的能力要好一些
logistic函数因为输出恒大于0,因此这个函数的输出作为输入的时候,会偏,因此对优化的性能不是很好。
比如在优化的时候,四个象限,logistic函数这种恒正的函数,只能在1、3象限优化,不能在第4象限优化,只能走之字形,因此效率会低。
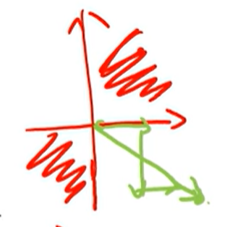
==解决这种非零中心化的方法==
- 归一化到零中心化
- 在函数的外面加一个可学习的参数 偏置b,缓解非零中心化带来的问题
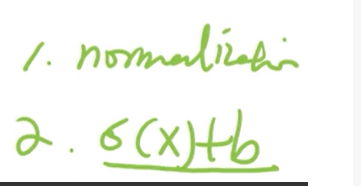
斜坡函数
代表函数是ReLU函数,也叫修正的线性单元
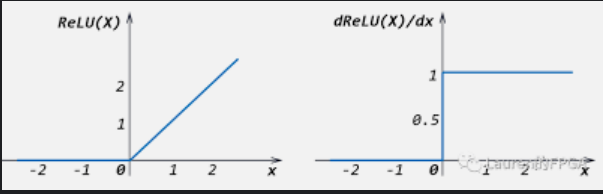
这种函数非常简单,目前的神经网络中大量的使用这种激活函数,一般激活函数首选ReLU

==ReLU函数的性质==
- 计算简单
- 生物学上的合理性,生物学家发现神经元兴奋的时候能够非常兴奋
- 优化性质非常好,因此右边的导数是1,因此在优化的时候,不会太小,也不会太大,从而更加有效的来学习参数
==ReLU存在的问题==
死亡ReLU问题,因为左边为0,会导致梯度消失,神经元无法更新权重参数了。
==ReLU问题解决==
- 通过归一化的方式来缓解死亡ReLU问题,使得数据的分散不要太集中。
- 初始化参数的时候,避免全部都初始化为负值
- 使用leaky ReLU,左边不要让其等于0,而是给一个很小的梯度
- 同时也可以将γ这个参数变成可学习的,即带参数的ReLU
==ReLU函数的非零中心化问题==
复合激活函数
==swish函数==
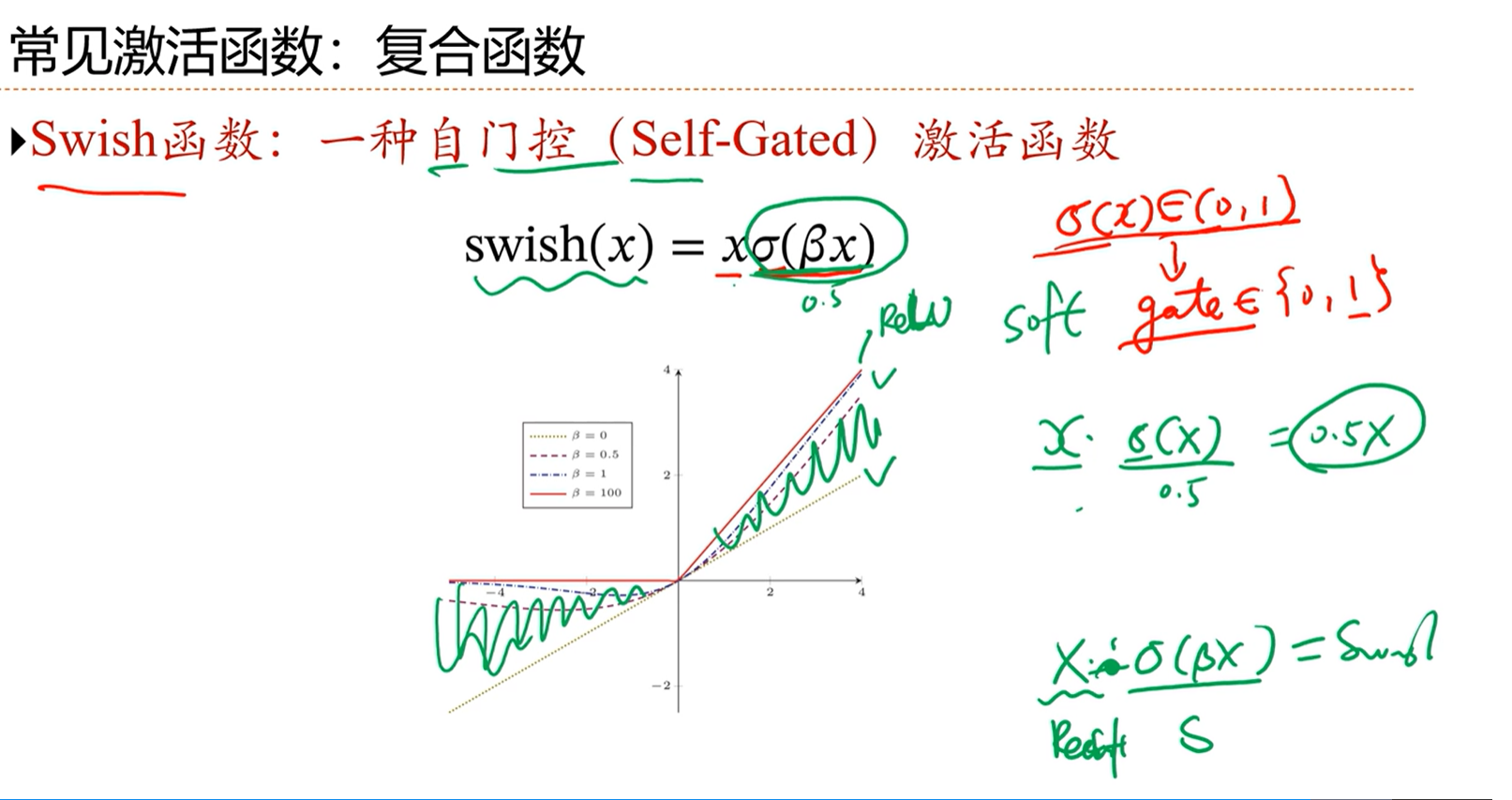
自门控函数,自己控制自己,xσ(βx)
这种函数能够通过变换β的值,实现在线性函数和ReLU函数之间变换,是一种非常灵活的函数
==高斯误差线性单元,GELU==

p(X<x)的形状和s型函数是类似的,因此这个GELU函数的形状和swish函数的形状基本是一样的
目前在比较新的模型中基本都是用GELU作为激活函数,这种函数优化的性质相对来说要好一些
常见的激活函数和导数的总结

[√] 4.2 - 神经网络
logistic激活函数的输出在0-1之间,如果只是希望非线性就够了,那么就优先采用ReLU函数。
logistic函数
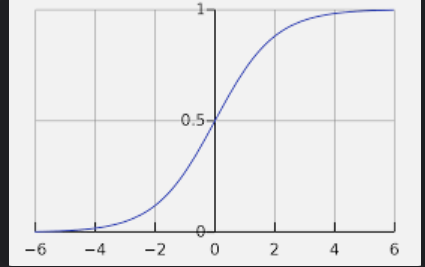
ReLU函数
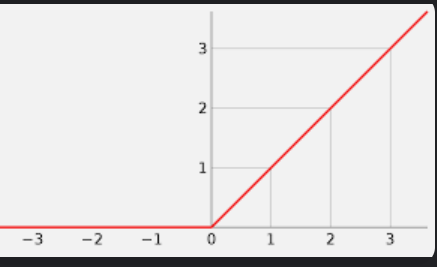
tanh函数

不是所有的网络都是通过梯度下降的方式来更新参数,比如hopfield网络

本课程会讲的3种网络
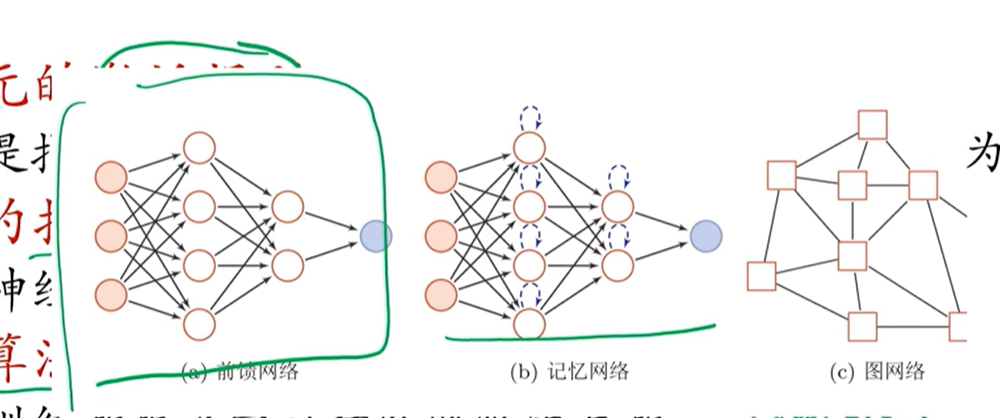
记忆网络,有循环边,因此就会有状态的概念,即历史状态是什么
图网络一般是一组神经元,因此用方形的来表示。
这三种网络是分开讲的,但是在实际应用中,通常是不同的网络相互组合来用的。
神经网络主要是连接主义模型,区别于符号主义模型。符号主义中,知识或者信息是用符号来定义的,连接主义中是信息是存在连接上的
连接主义的模型是分布式并行处理网络,这种网络主要就是神经网络。
连接主义的三点:
- 由网络来共同表示信息,而不是像符号主义一样一个符号就表示一个信息
- 知识是定义在单元之间的连接上的,单元之间连接强度的改变可以来学习新的知识
神经网络就是一个典型的连接主义模型
[√] 4.3 - 前馈神经网络
网络结构
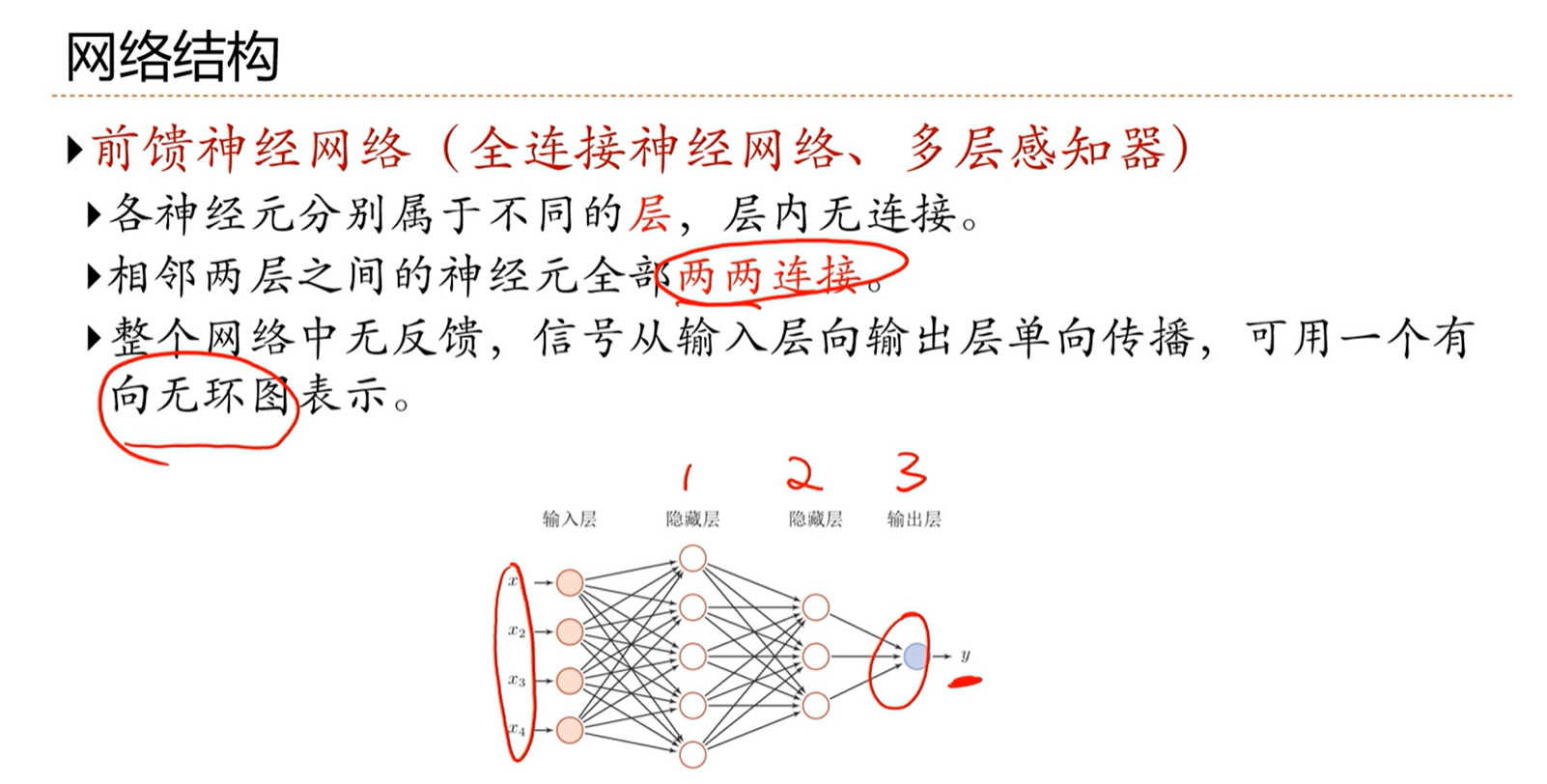
相邻层之间的神经元是全部两两连接(全连接)
单向传递
层内无连接
定义一个网络的层数的时候,不算输入层,因此上面的网络一共有3层
前馈网络
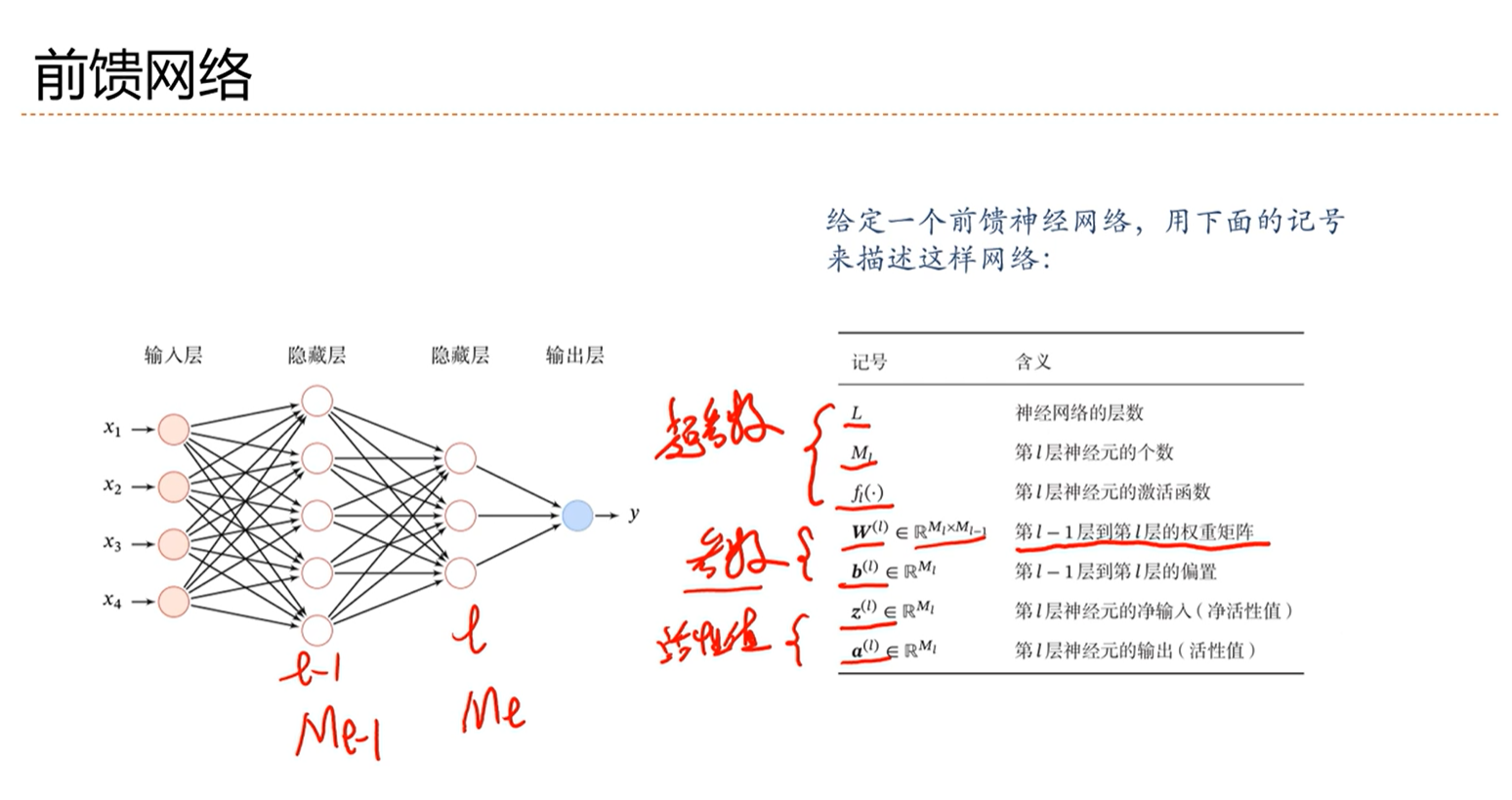
信息传递过程
第l层的传递过程:
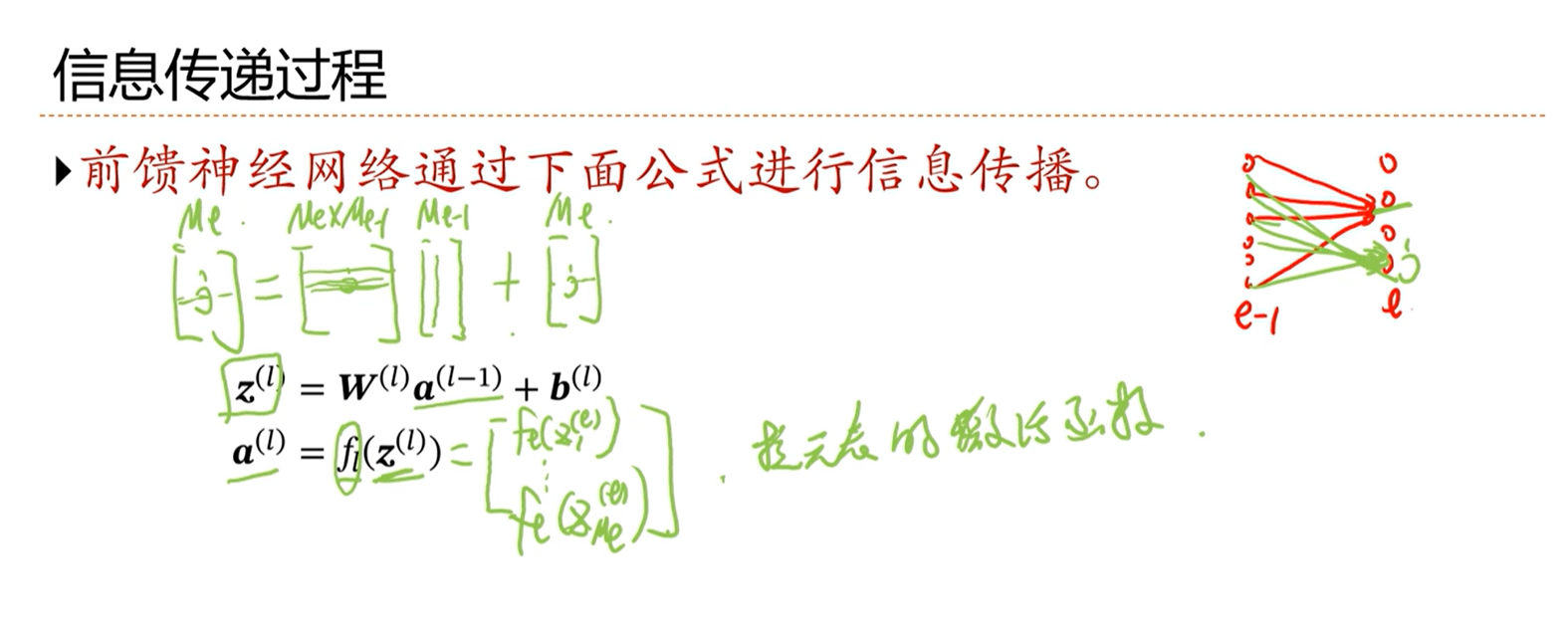
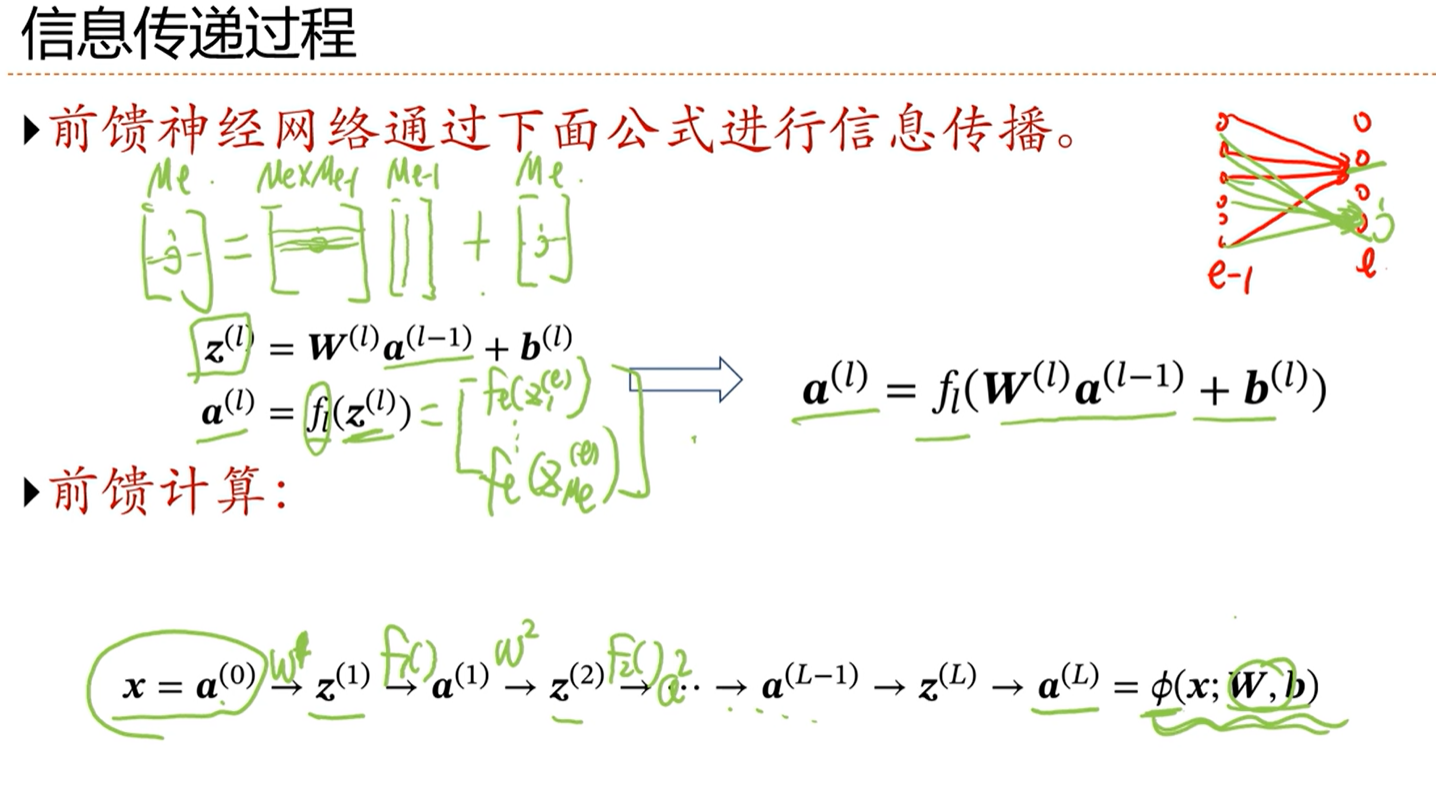
-> 通用近似定理

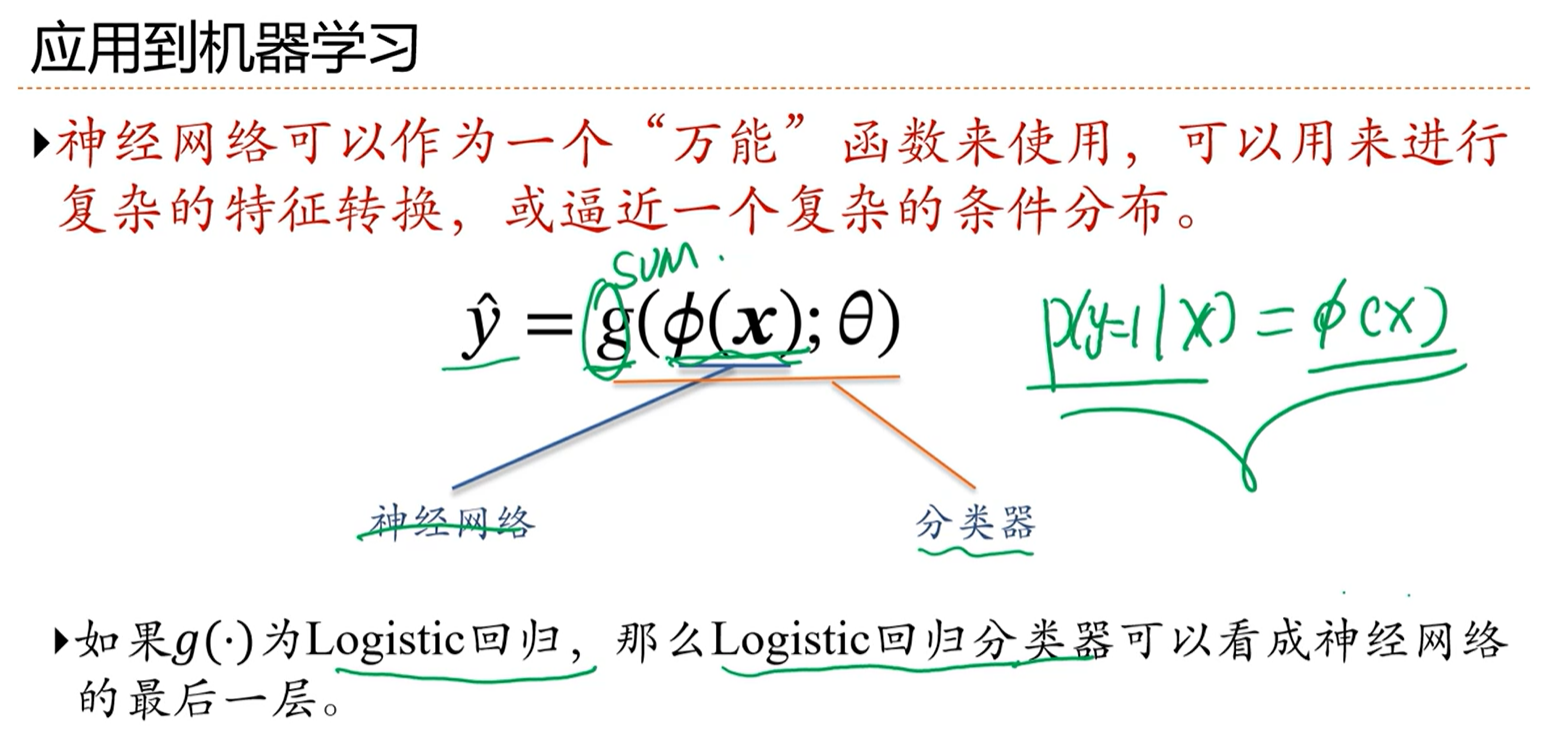
-> 应用到机器学习
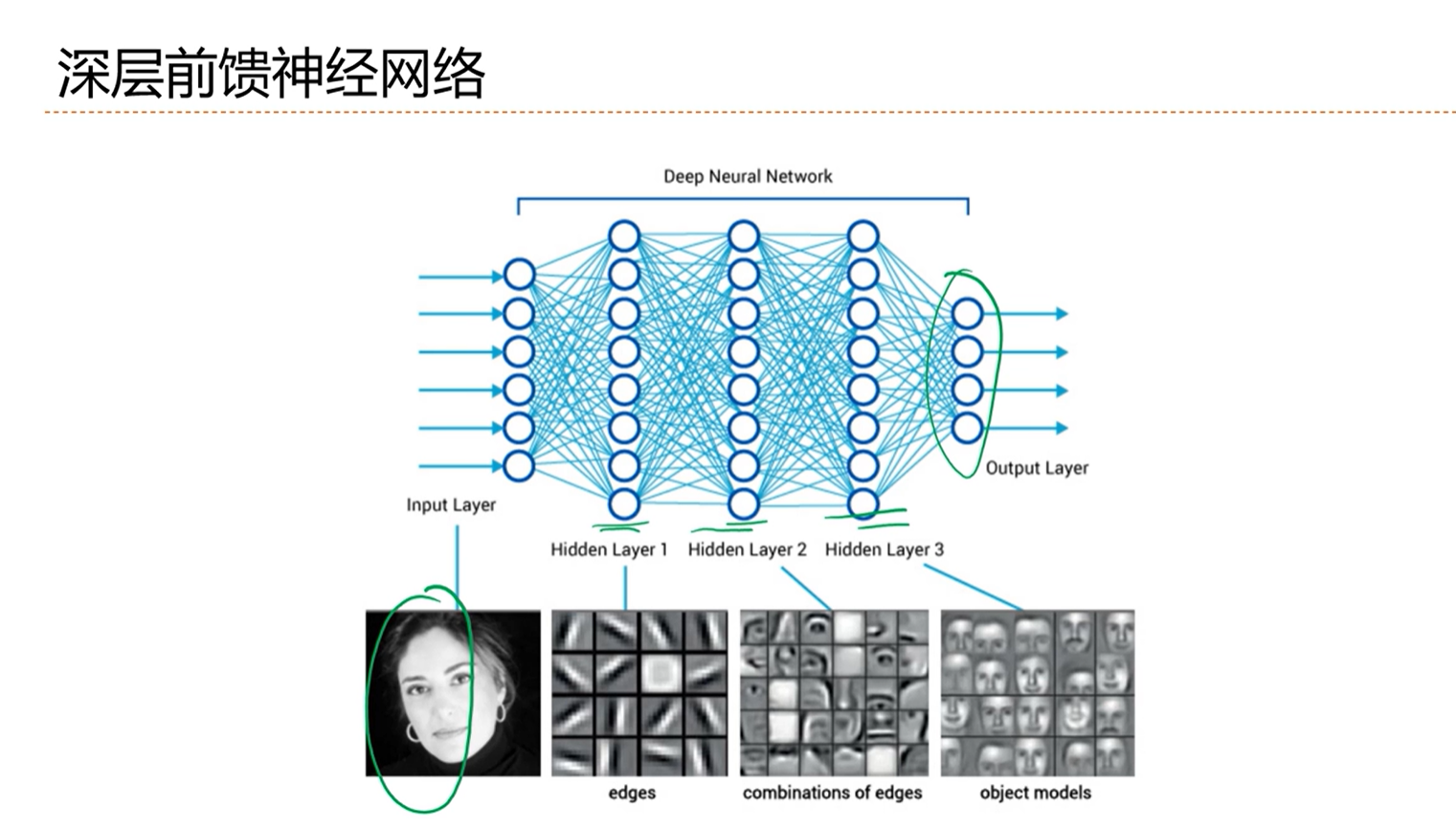
-> 深层前馈神经网络
前馈神经网络进行分类任务
-> 参数学习

神经网络用作多分类任务,相当于最后一层设计C个神经元。
softmax这个激活函数和其它的激活函数的区别是,这个函数的输出内容不光和前一层的内容相关,还和同一层的其它神经元的内容相关

-> 如何计算梯度

[√] 4.4 - 反向传播算法
-> 矩阵微积分
分母布局就是使用列向量表示

-> 链式法则

-> 计算梯度
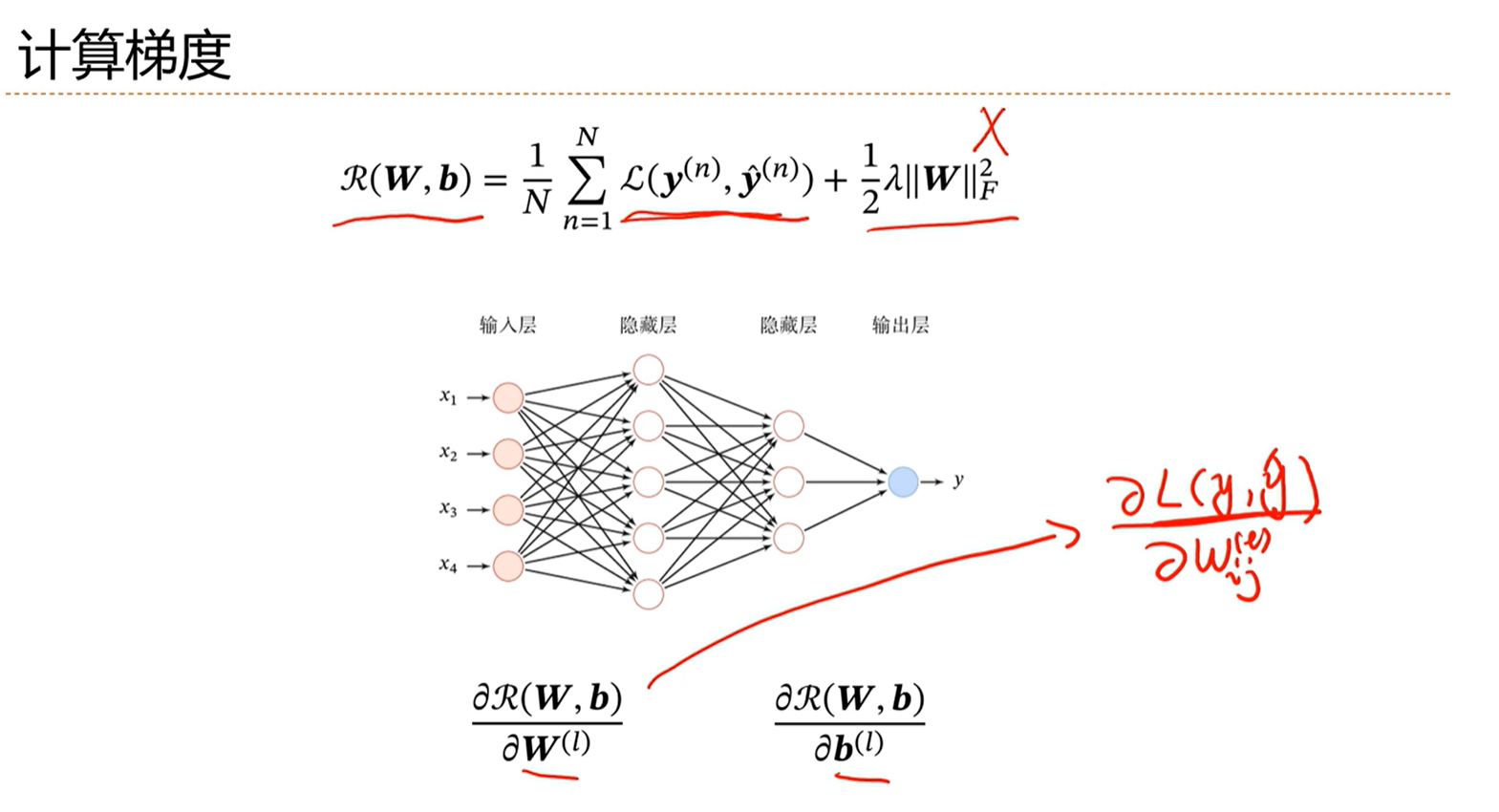
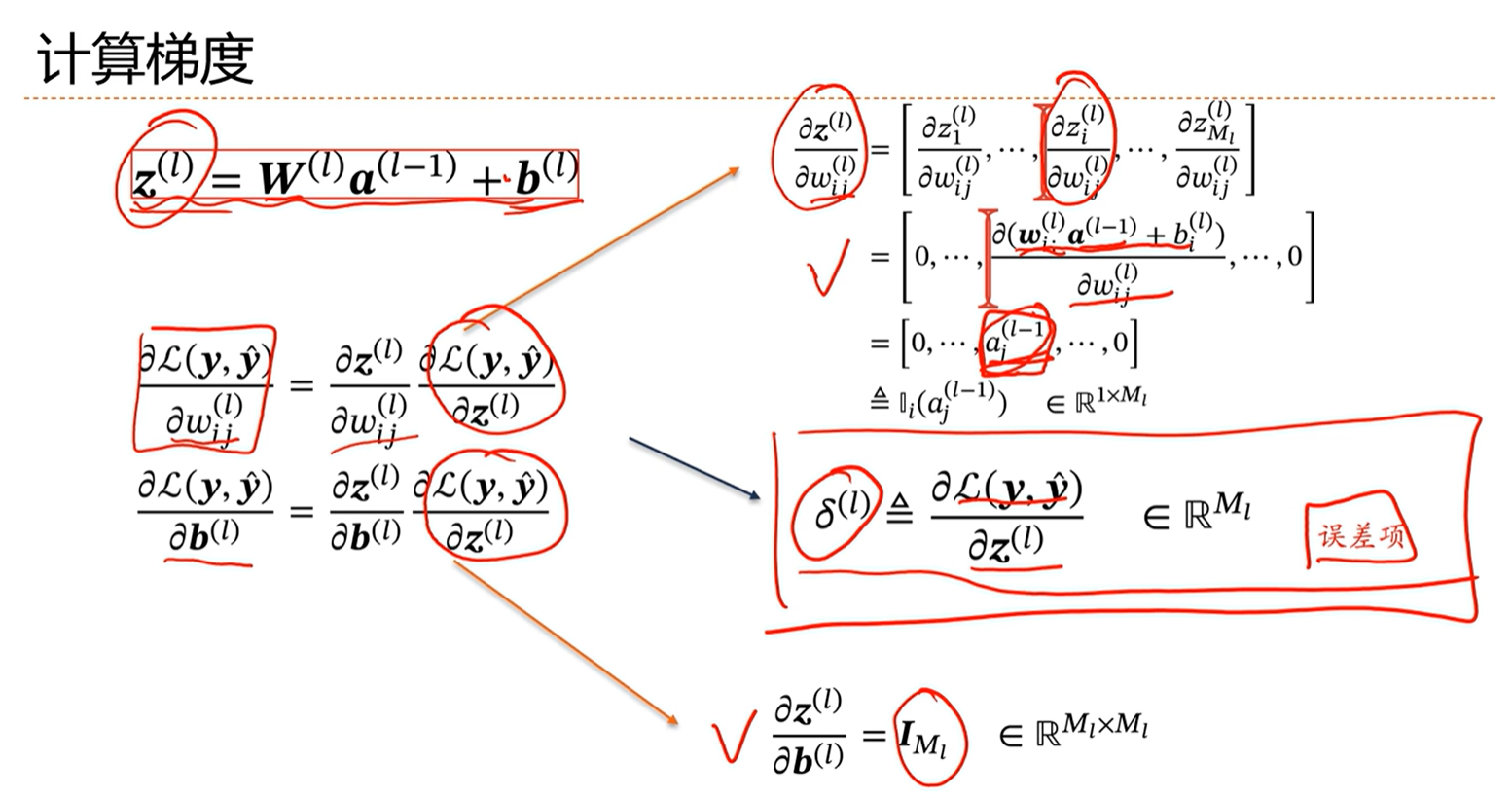
上面的1、3项已经有了,核心是计算第二项。第二项定义为第L层的误差项。
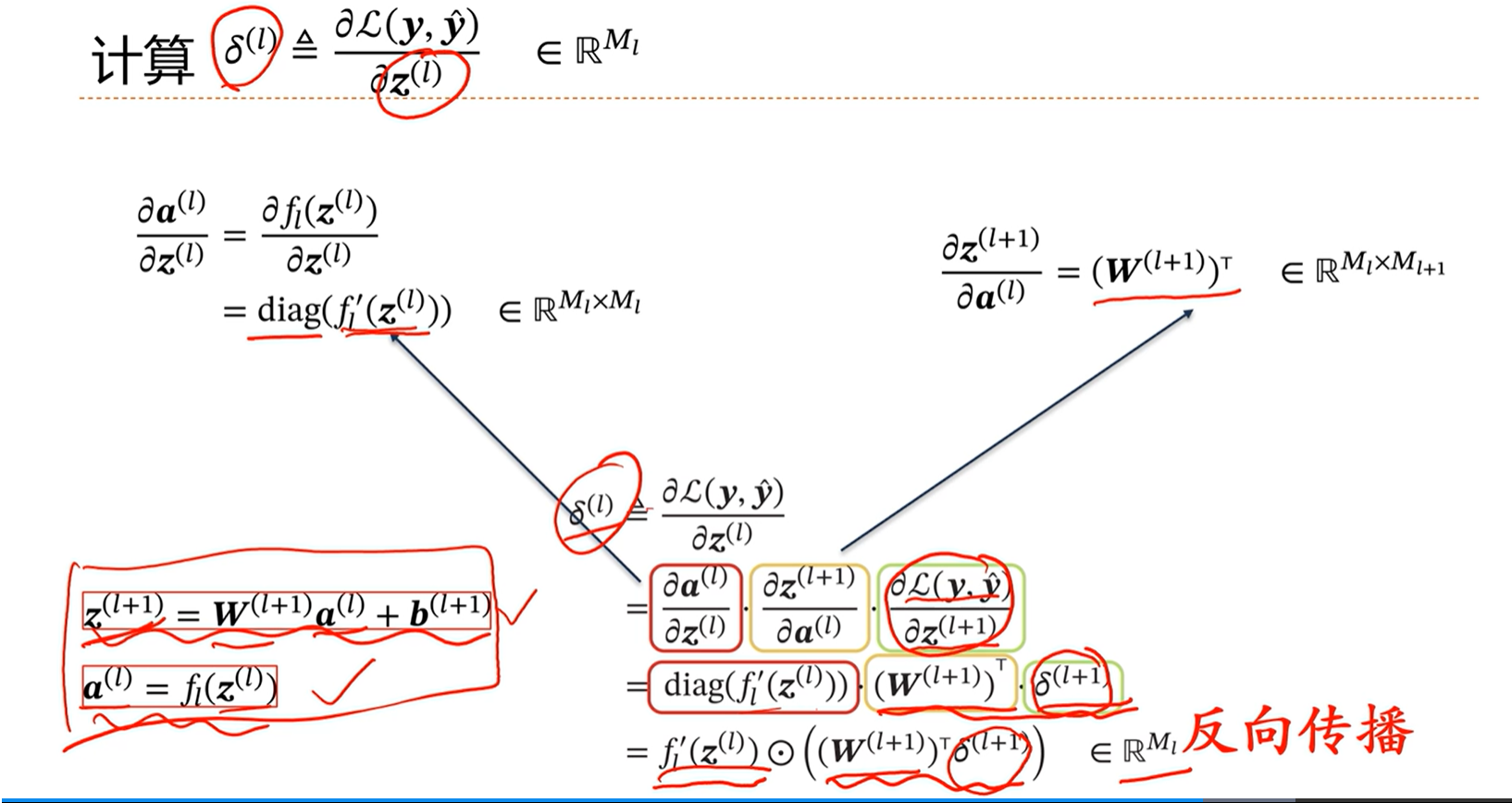
通过上面的推导能够看出,第L层的导数,能够通过第L+1层的导数以及第L+1的权重等推导出,因此这里得到反向传播的链式法则。
即前面的层能够通过后面的层推出,因此从最后一层开始,能够逐层的推导出前面层的导数(梯度)。然后通过比如梯度下降算法优化权重参数,就能够进行模型训练。
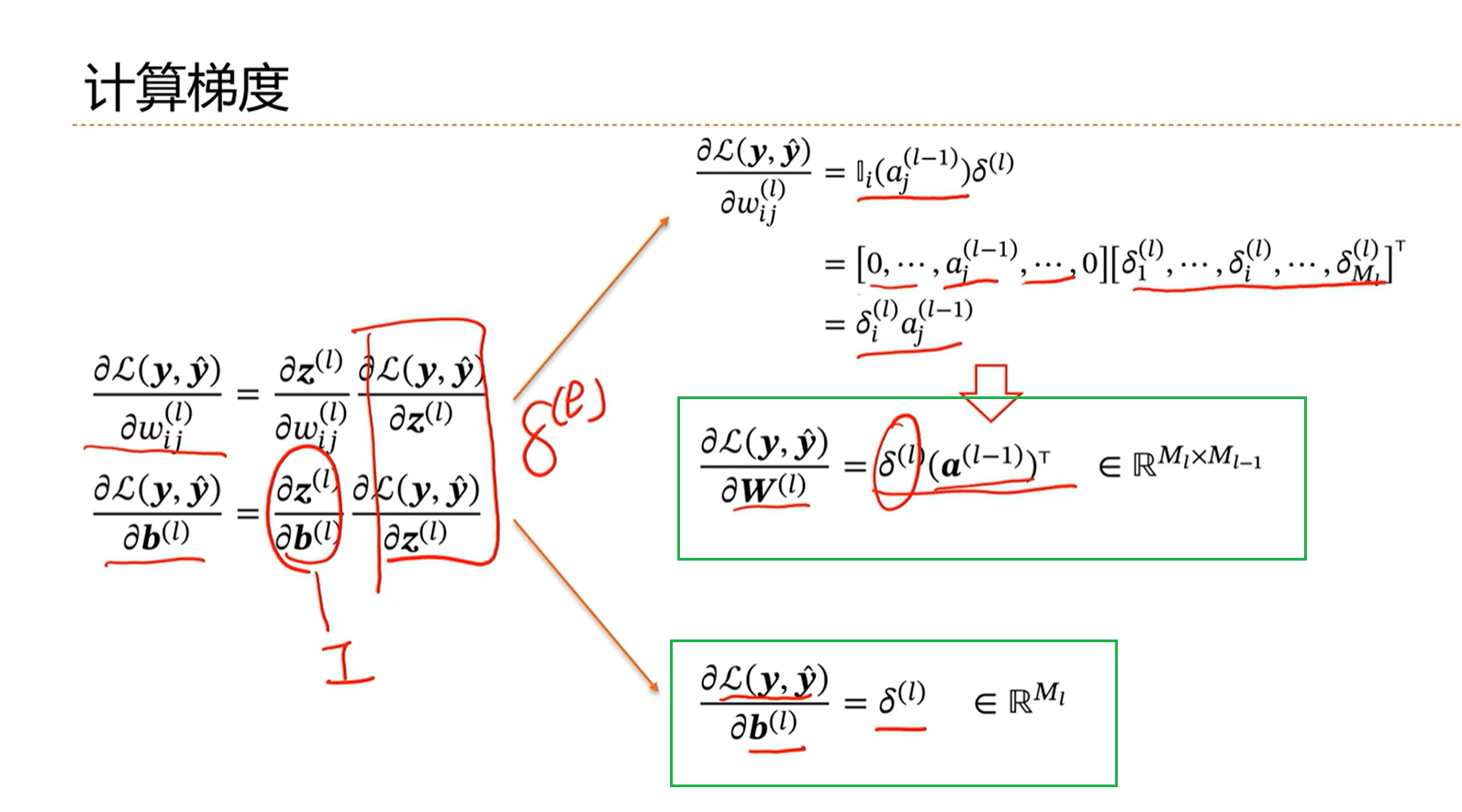
由上图看出,损失函数对第L层的w和b的导数,能够通过第L+1层的导数和第L-1层的激活层求出。
-> 使用反向传播算法的随机梯度下降训练过程

先前馈计算每一层的Z_l和A_l,其中A_l最后在梯度的反向传播计算的时候是需要用到的。
然后反向传播计算每一层参数的导数
最后用梯度下降算法更新参数
直到在验证集V上的错误率不再下降则停止训练
最后得到w和b
[√] 4.5 - 计算图与自动微分

-> 计算图与自动微分
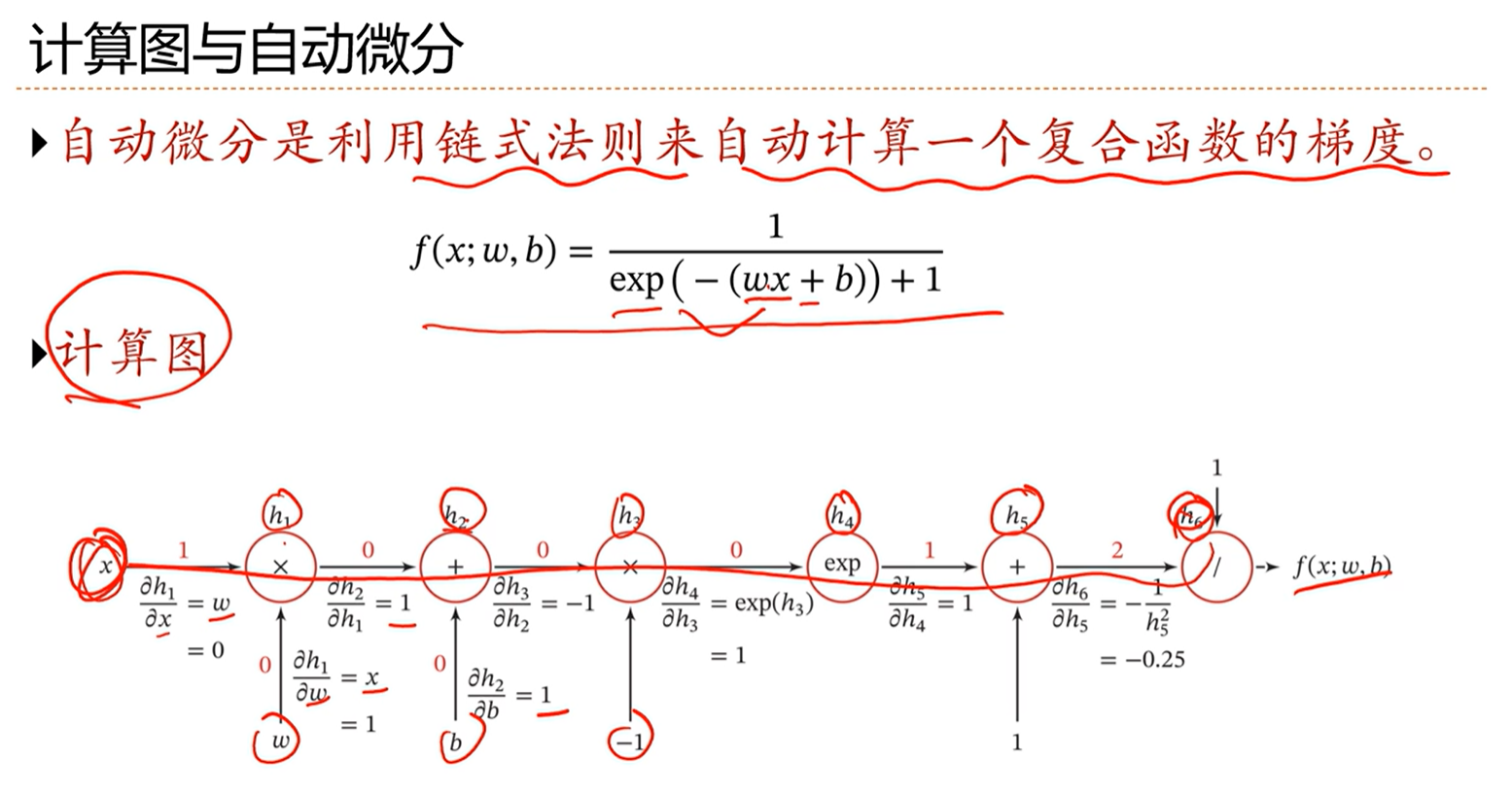
-> 计算图
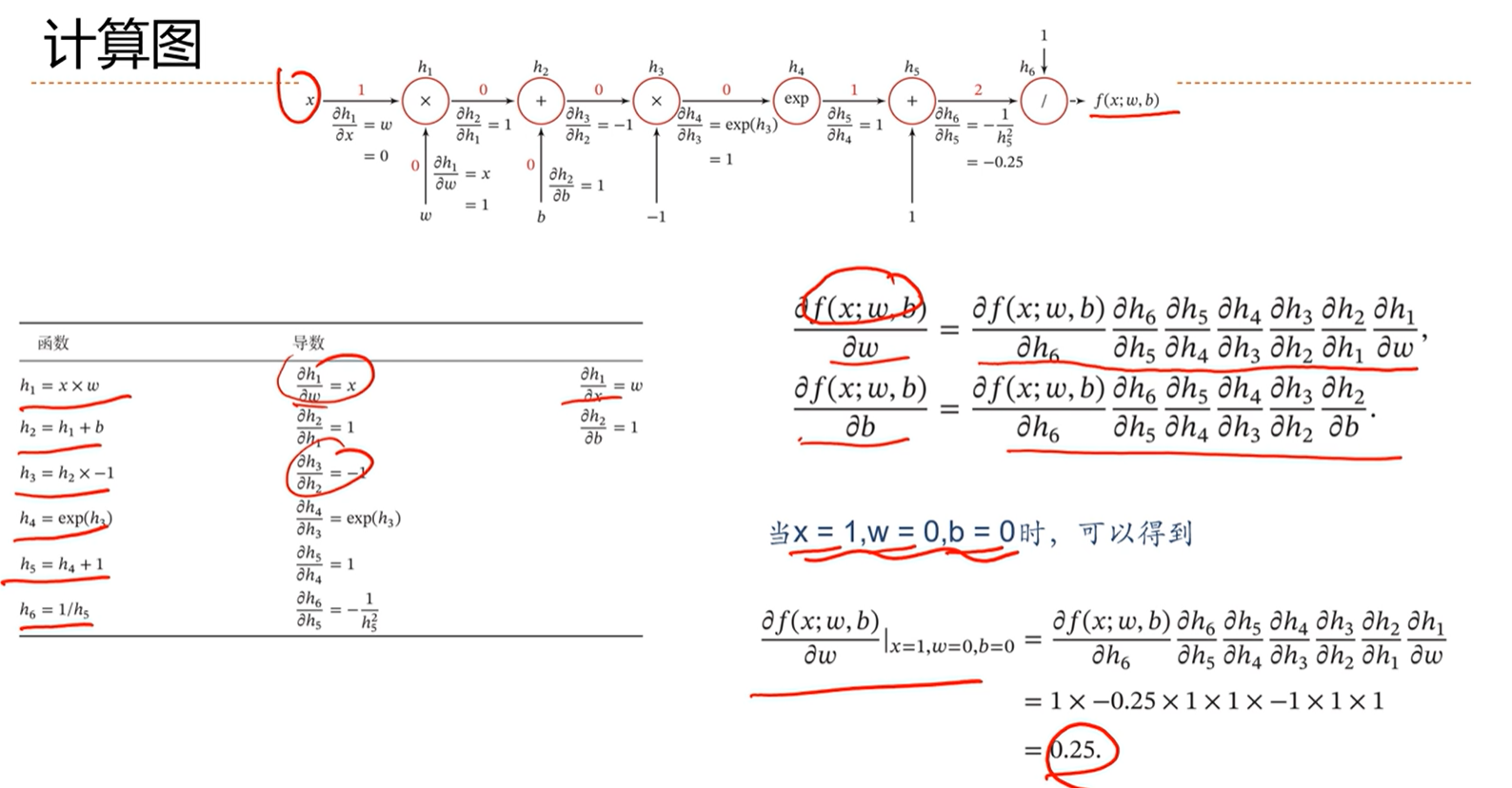
通过上面的这种链式的计算方法,框架能够自动计算梯度,因此就不用人工计算,非常方便。
-> 自动微分
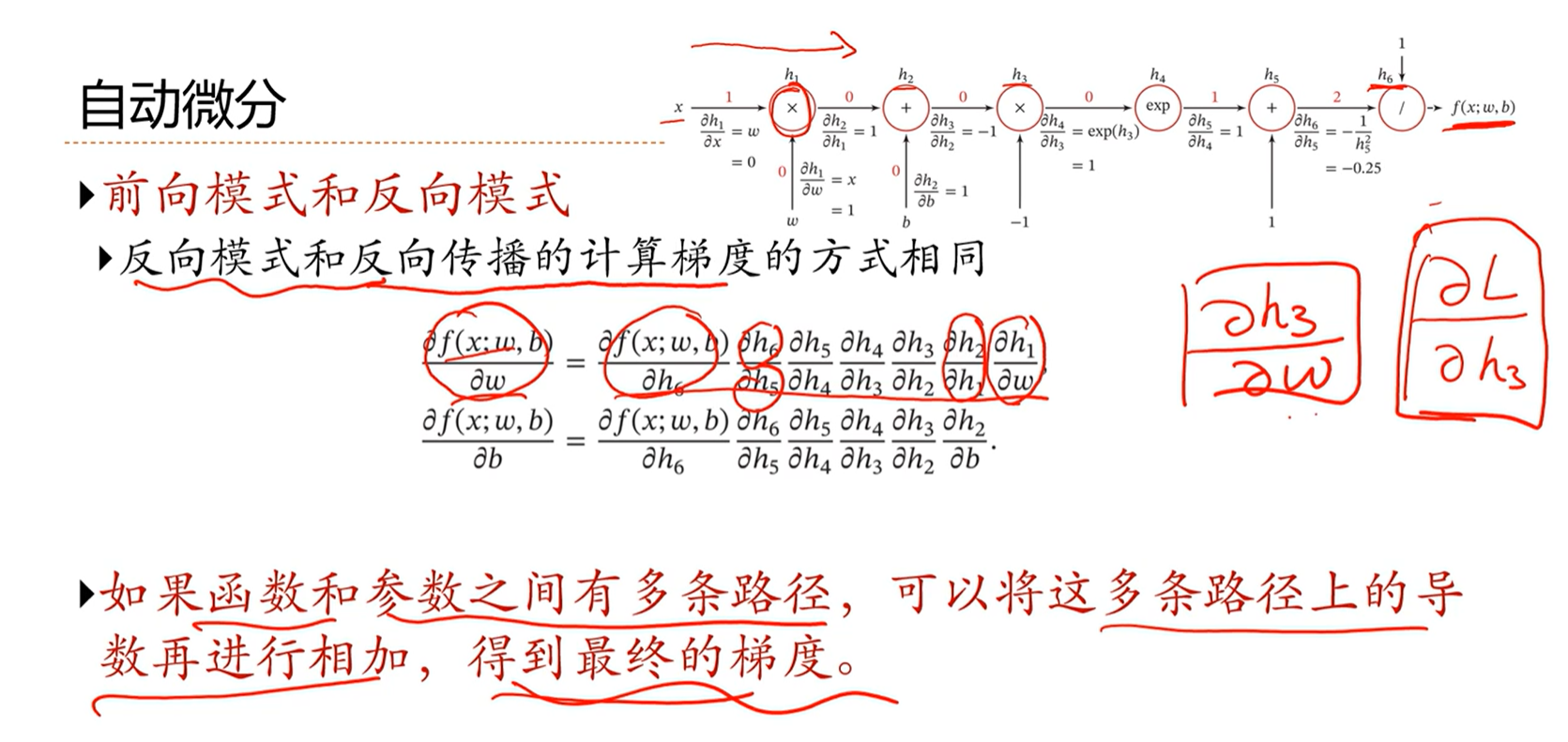
前向模式和反向模式的不同在于,前向模式由于是从前往后计算梯度链式法则中的每项,因此在计算的过程中需要保留中间项,如果链式非常长的话,那么需要保留的中间项非常多;因此一般使用反向模式。
-> PyTorch例子

-> 反向传播算法(自动微分的反向模式)

-> 静态计算图和动态计算图

静态计算图的计算效率比较高
动态计算图更加的灵活
-> 如何实现


keras在tensorflow的基础上,又进行了一次封装
-> 深度学习的三个步骤
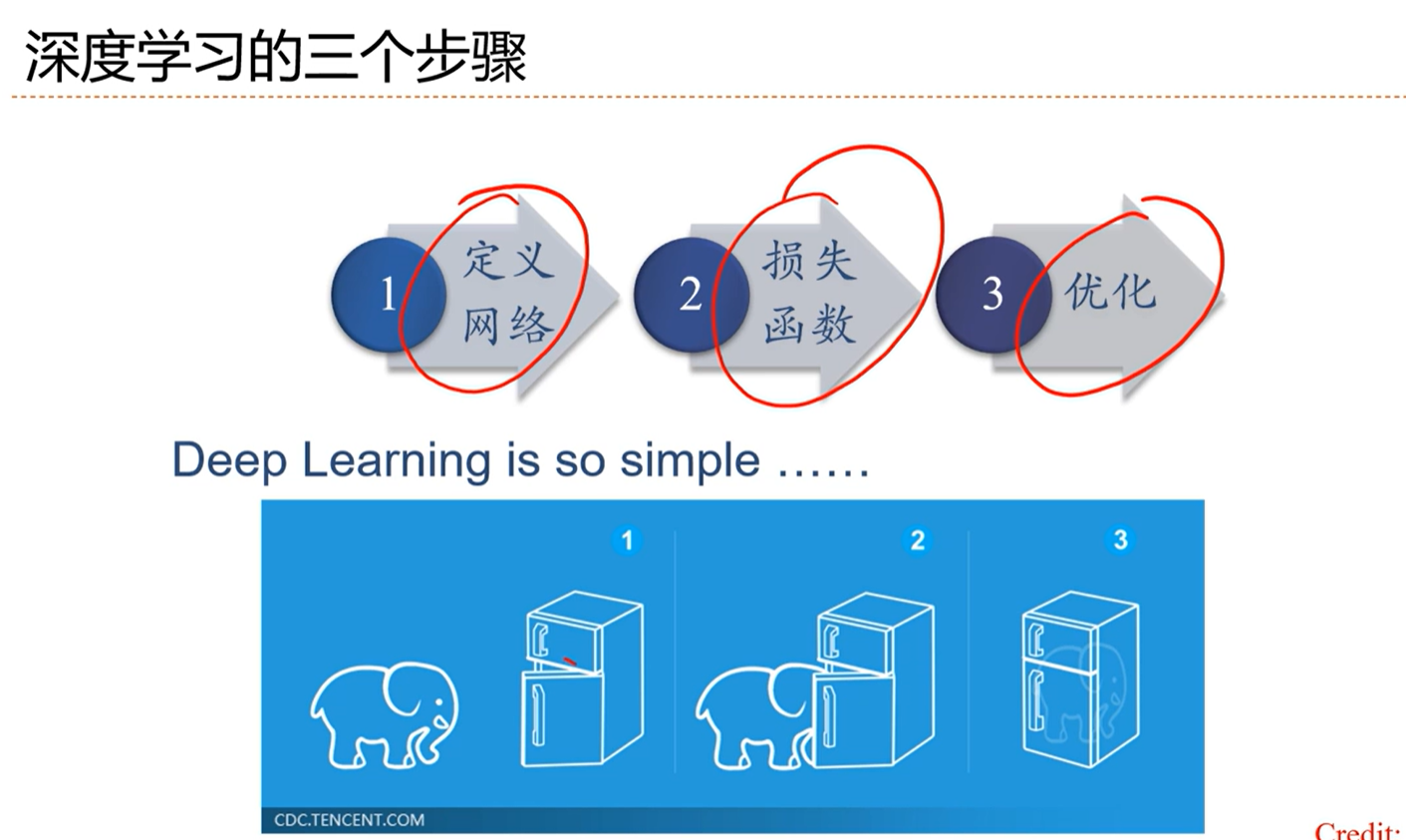
[√] 4.6 - 优化问题
-> 神经网络优化问题之非凸优化问题
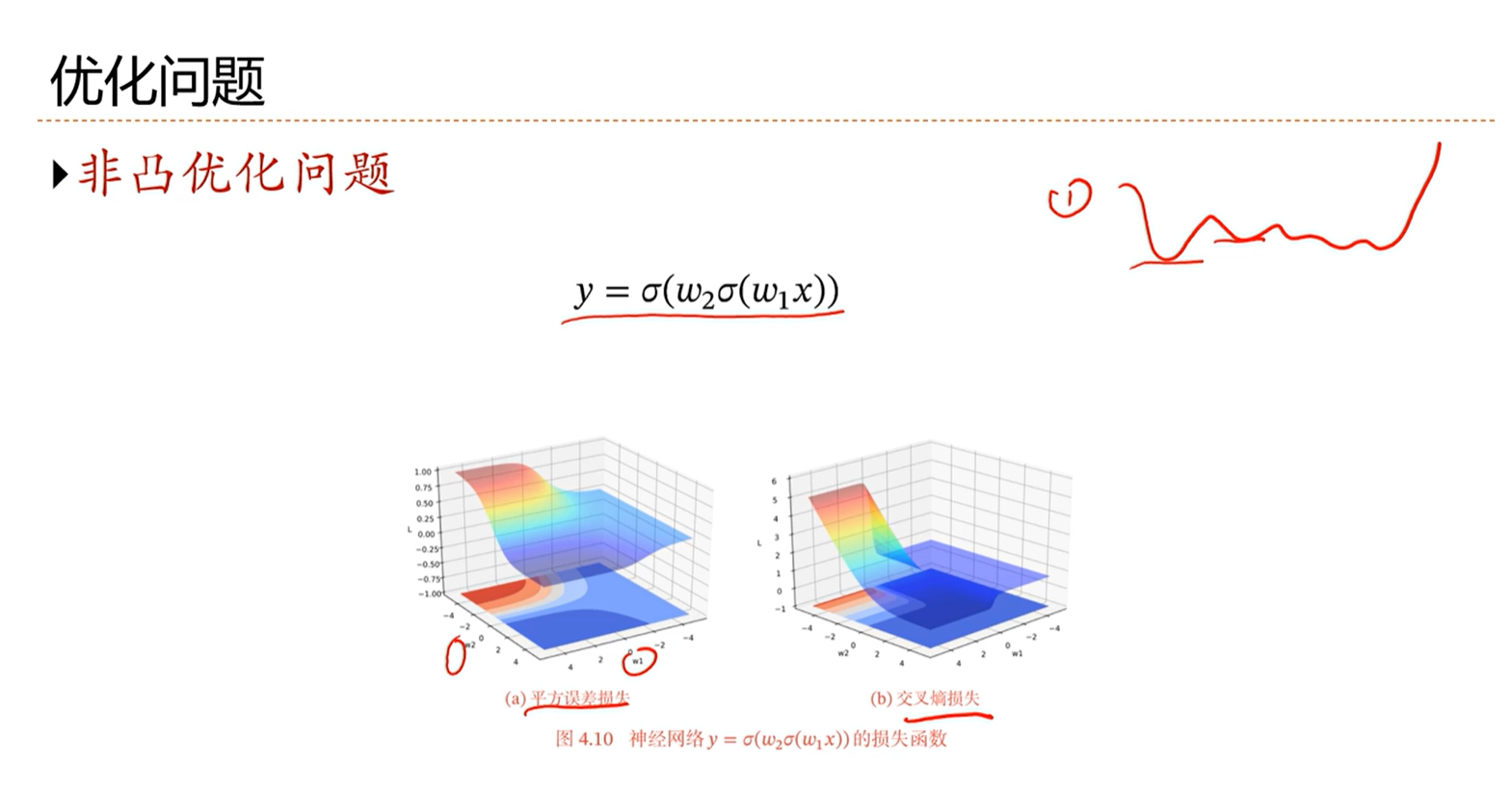
非凸函数,优化困难,比如存在局部最优问题,局部最小值如何再找到全局最小值是非常困难的。
另外,在高维中存在鞍点问题,使用梯度下降方法到了鞍点就走不动了
-> 神经网络优化问题之梯度消失问题
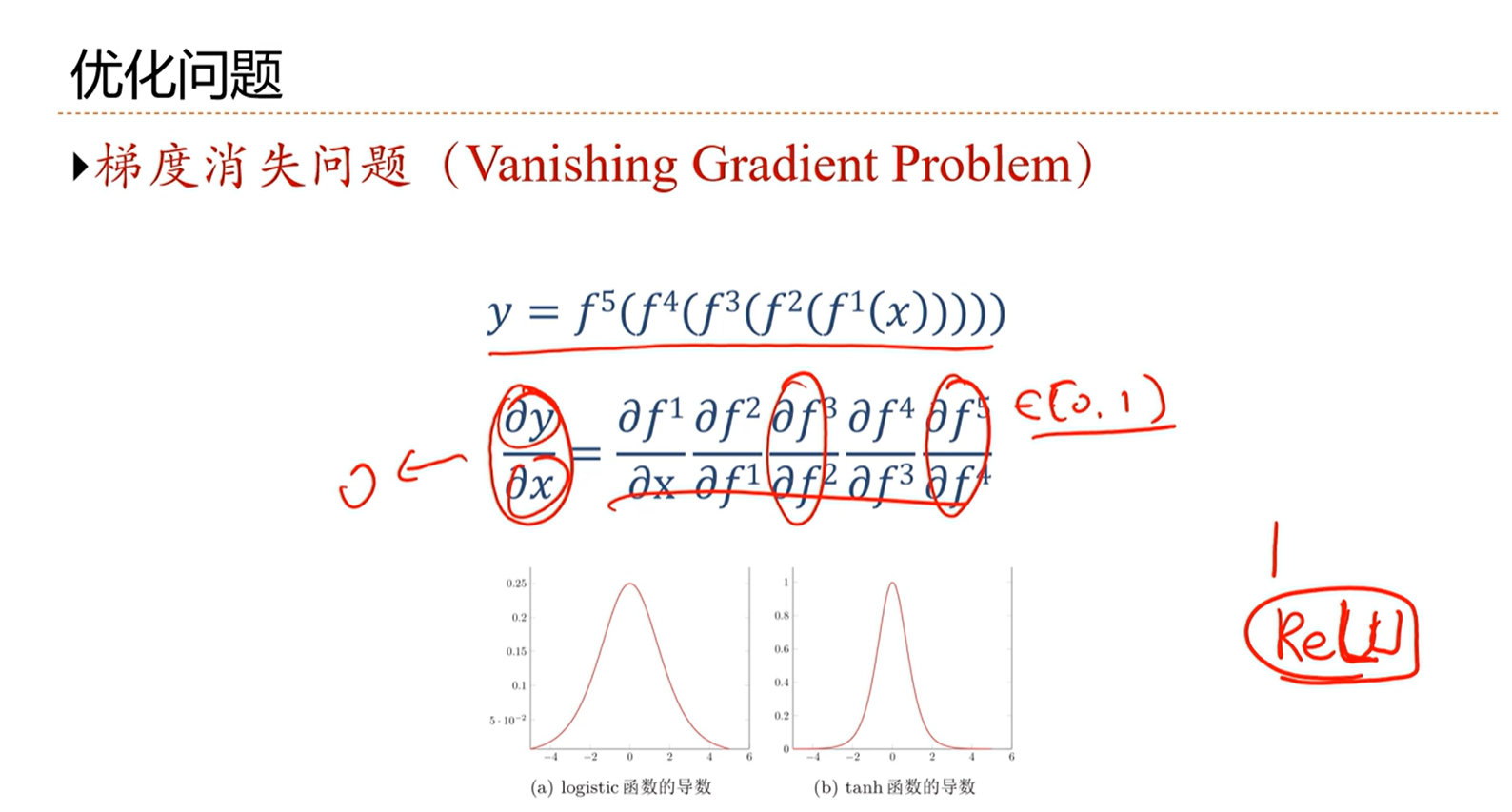
当梯度的链式很长,每个因子都在0-1之间,那么最后梯度整体就非常小,非常接近于0,这就是梯度消失问题,会导致更新很慢、很难学。
因此让激活函数最后在1左右是最好的,不能太小,也不能太大。这也是为什么激活函数推荐使用ReLU函数。因为ReLU函数在正的范围梯度是1.
-> 优化问题
