043 - 文章阅读笔记：组卷积

原文链接：

组卷积（group convolution） - CSDN - 专栏：深度学习 - 草帽-路飞

卷积中的分组卷积 - CSDN - 专栏：深度学习 - 草帽-路飞

于 2020-05-23 23:15:25 发布

说明分组卷积之前我们用一张图来体会一下一般的卷积操作。

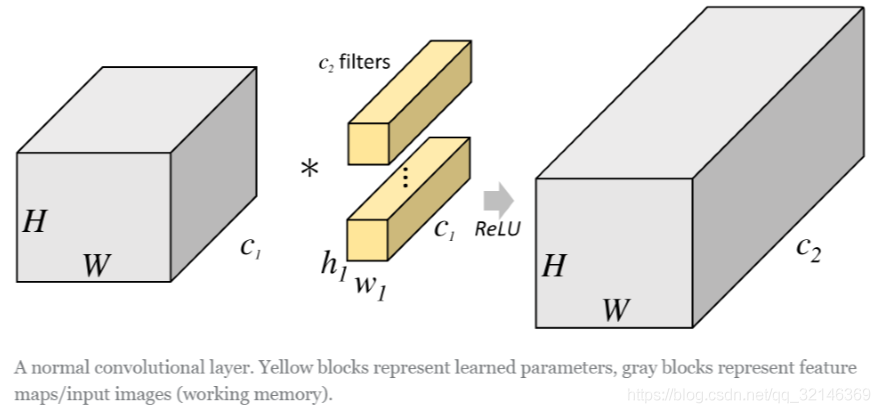
一般的卷积会对输入数据的整体一起做卷积操作，即输入数据：H1×W1×C1；而卷积核大小为h1×w1，通道 为C1，一共有C2个，然后卷积得到的输出数据就是H2×W2×C2。

这里我们假设输出和输出的分辨率是不变的。主要看这个过 程是一气呵成的，这对于存储器的容量提出了更高的要求。

alec：

• 一般的卷积会对输入数据的整体一起做卷积操作，即输入数据：H1×W1×C1；而卷积核大小为h1×w1，通道 为C1，一共有C2个，然后卷积得到的输出数据就是H2×W2×C2。
• 一般卷积：每个卷积核的深度为C1，一共有C2个卷积核。输出的通道数为C2。
• 一般卷积是一次性对输入全部的通道做卷积，对存储器的容量提出了很高的要求。
• 但是分组卷积没有那么多的参数。

但是分组卷积明显就没有那么多的参数。先用图片直观地感受一下分组卷积的过程。对于上面所说的同样的一个问题，分组卷积就如下图所示：

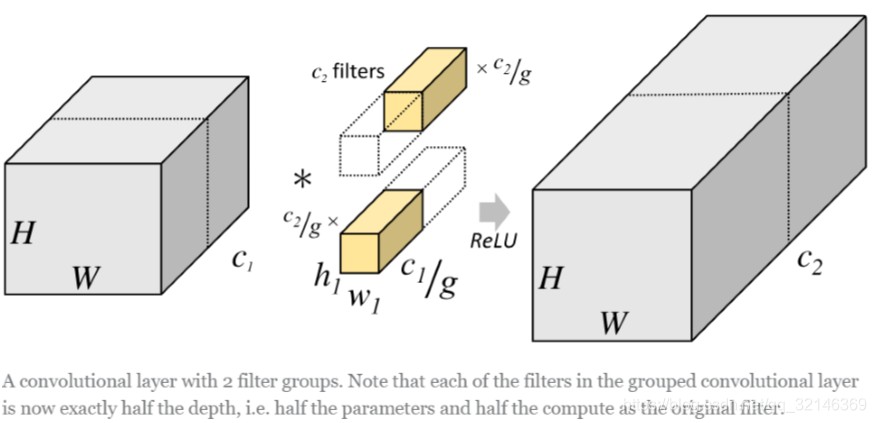
可以看到，图中将输入数据分成了2组（组数为g），需要注意的是，这种分组只是在深度上进行划分，即某几个通道编为一 组，这个具体的数量由（C1/g）决定。因为输出数据的改变，相应的，卷积核也需要做出同样的改变。即每组中卷积核的深度 也就变成了（C1/g），而卷积核的大小是不需要改变的，此时每组的卷积核的个数就变成了（C2/g）个，而不是原来的C2 了。然后用每组的卷积核同它们对应组内的输入数据卷积，得到了输出数据以后，再用concatenate的方式组合起来，终的 输出数据的通道仍旧是C2。也就是说，分组数g决定以后，那么我们将并行的运算g个相同的卷积过程，每个过程里（每组）， 输入数据为H1×W1×C1/g，卷积核大小为h1×w1×C1/g，一共有C2/g个，输出数据为H2×W2×C2/g。

alec：

• 一般卷积，是在整个输入的全部通道一起卷积。
• 分组卷积，是对输入在通道维度上分组，将几个特征图分为一组，分别进行各自的卷积。
• 分组卷积被认为是正则的效果。
• 分组卷积，能够极大的减少参数量。将输入的通道分为几组、那么参数量就减少几倍。比如讲输入通道分为8组分别卷积，那么总体的参数量将减少为原来的1/8。

举个例子：
Group conv本身就极大地减少了参数。比如当输入通道为256，输出通道也为256，kernel size为3×3，不做Group conv参数 为256×3×3×256。实施分组卷积时，若group为8，每个group的input channel和output channel均为32，参数为 8×32×3×3×32，是原来的八分之一。而Group conv后每一组输出的feature maps应该是以concatenate的方式组合。 Alex认 为group conv的方式能够增加 filter之间的对角相关性，而且能够减少训练参数，不容易过拟合，这类似于正则的效果。