7 - 网络优化与正则化 - 书籍2

本文最后更新于：3 个月前

[√] 7.4 参数初始化

alec：

  • 神经网络的参数学习是一个非凸优化问题。
  • 当使用梯度下降法来进行网络参数优化时，参数初始值的选取十分关键，关系到网络的优化效率和泛化能力。（神经网络的初始参数值非常重要）
  • 此外，由于神经网络优化时出现的对称权重现象（参见第4.4.1节），神经网络的参数不能初始化为相同的值，需要有一定的差异性。（神经网络的参数初始值不能初始化为相同的值）

常用的参数初始化的方式通常有以下三种：

  • 随机初始化：最常用的参数初始化策略，通过一个随机采样函数来生成每个参数的初始值。
  • 预训练初始化：一种在实践中经常使用的初始化策略，如果目标任务的训练数据不足，可以使用一个已经在大规模数据上训练过的模型作为参数初始值。预训练模型在目标任务上的学习过程也称为精调Fine-Tuning。
  • 固定值初始化：对于神经网络中的某些重要参数，可以根据先验知识来初始化。比如对于使用ReLU激活函数的全连接层，其偏置通常可以设为比较小的正数（比如0.01），从而确保这一层的神经元的梯度不为0，避免死亡ReLU现象。
  • tune，调整、微调

虽然预训练初始化通常具有更好的收敛性和泛化性，但是灵活性不够，不能在目标任务上任意地调整网络结构。因此，好的随机初始化方法对训练神经网络模型来说依然十分重要。在本节我们主要介绍两种随机初始化方法：基于固定方差的参数初始化和基于方差缩放的参数初始化。

[√] 7.4.1 基于固定方差的参数初始化

一种最简单的随机初始化方法是从一个固定均值(通常为 0)和方差$\sigma^2$的分布中采样来生成参数的初始值。基于固定方差的参数初始化方法主要有高斯分布初始化和均匀分布初始化两种：

  • 高斯分布初始化：使用一个高斯分布$\mathscr{N}(0, \sigma^2)$对每个参数进行随机初始化。
  • 均匀分布初始化：在一个给定的区间$[-r, r]$内采用均匀分布来初始化。

高斯分布和均匀分布初始化的实现方式可以参考第4.4.1节参数初始化代码。

[√] 7.4.2 基于方差缩放的参数初始化

alec：

  • 初始化一个深度网络时，为了缓解梯度消失或爆炸问题，我们尽可能保持每个神经元的输入和输出的方差一致。
  • 根据神经元的连接数量来自适应地调整初始化分布的方差，这类方法称为方差缩放（Variance Scaling）。
  • Xavier初始化是参数初始化中常用的方法，根据每层的神经元数量来自动计算初始化参数方差。
  • 在计算出参数的理想方差后，可以通过高斯分布或均匀分布来随机初始化参数。
  • 在计算出参数的理想方差后，可以通过高斯分布或均匀分布来随机初始化参数。若神经元采用Tanh函数，并采用高斯分布来随机初始化参数，连接权重$w_i^{(l)}$可以按$\mathscr{N}(0, \frac{2}{M_{l-1} + M_l})$的高斯分布进行初始化，其中$M_{l-1}$是第$l-1$层神经元个数。
[√] 7.4.2.1 模型构建

首先定义xavier_normal_std函数，根据$l$层和$l-1$层神经元的数量计算理想标准差。值得注意的是，在paddle.normal API中，通过指定标准差的值来生成符合正态分布的张量，因此，这里需要计算标准差。代码实现如下：

1
2
3
# 计算标准差
def xavier_normal_std(input_size, output_size):
    return np.sqrt(2 / (input_size + output_size))

alec：

  • Xavier初始化就是基于方差缩放的参数初始化，根据每层的神经元数量自动计算用于初始化参数的方差。
  • Xavier初始化适用于Logistic激活函数和Tanh激活函数。
  • 对于不同激活函数，高斯分布的方差和均匀分布的$r$值计算是不同的。
  • xavier_normal_std定义针对Tanh激活函数的情况。

定义一个全连接前馈网络（即多层感知器）MLP算子，实例化网络时可以通过layers_size指定网络每层神经元的数量，通过init_fn_name指定网络中参数初始化方法(Xavier高斯分布初始化、Xavier均匀分布初始化或$\mathscr{N}(0, 1)$高斯分布初始化)，init_fn指定计算初始化时均值或数值范围的函数，act_fn指定激活函数。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class MLP(nn.Layer):
    def __init__(self, layers_size, init_fn_name, init_fn, act_fn):
        """
        多层网络初始化
        输入：
            - layers_size: 每层神经元的数量
            - init_fn_name: 网络中参数初始化方法，可以为 'normal'或'uniform'
            - init_fn: 函数，用来计算高斯分布标准差或均匀分布r值
            - act_fn: 激活函数
        """
        super(MLP, self).__init__()
        self.linear = nn.Sequential()
        self.num_layers = len(layers_size) - 1
        for i in range(self.num_layers):
            input_size, output_size = layers_size[i], layers_size[i + 1]
            # 计算高斯分布的初始化参数
            if init_fn_name == 'normal':
                # Xavier高斯分布初始化，计算方差
                self.linear.add_sublayer(str(i), nn.Linear(input_size, output_size,
                                           weight_attr=nn.initializer.Normal(mean=0, std=init_fn(input_size, output_size))))
            elif init_fn_name == 'uniform':
                r = init_fn(input_size, output_size)
                self.linear.add_sublayer(str(i), nn.Linear(input_size, output_size, weight_attr=nn.initializer.Uniform(low=-r, high=r)))
            else:
                self.linear.add_sublayer(str(i), nn.Linear(input_size, output_size, weight_attr=nn.initializer.Normal()))
        self.act_fn = act_fn()
        self.z = {}

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        前向计算
        """
        y = X
        for num_layer in range(self.num_layers):
            y = self.linear[num_layer](y)
            if num_layer != self.num_layers - 1:
                y = self.act_fn(y)
            self.z[num_layer] = y
        return y
[√] 7.4.2.2 观察模型神经元的方差变化
[√] 高斯分布初始化

定义网络每层神经元的数量，指定激活函数和参数初始化方式，通过Xavier高斯分布初始化网络。代码实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
paddle.seed(0)

# 定义网络每层神经元的数量
layers_size = [100, 200, 400, 300, 200, 100]
# 指定激活函数
activate_fn = paddle.nn.Tanh
# 指定参数初始化方式
init_fn_name = 'normal'

model = MLP(layers_size, init_fn_name, init_fn=xavier_normal_std, act_fn=activate_fn)
inputs = paddle.normal(shape=[1, 100], std=0.1)
y = model(inputs)
1
2
运行时长: 11毫秒
结束时间: 2022-12-24 16:17:09

打印每层神经元输出的方差，观察每层的方差值。

1
2
for i in range(len(model.z) - 1):
    print('layer %d: , %f'%(i, model.z[i].numpy().var()))
1
2
3
4
layer 0: , 0.005416
layer 1: , 0.003292
layer 2: , 0.003820
layer 3: , 0.004489

从输出结果看，Xavier初始化可以尽量保持每个神经元的输入和输出方差一致。

[√] 均匀分布初始化

若采用区间为$[-r, r]$的均匀分布来初始化$w_i^{(l)}$，则$r$的取值为$\sqrt{\frac{6}{M_{l-1} + M_l}}$。定义xavier_uniform_r，计算均匀分布$r$的值。代码实现如下：

1
2
def xavier_uniform_r(input_size, output_size):
    return np.sqrt(6 / (input_size + output_size))
1
2
运行时长: 4毫秒
结束时间: 2022-12-24 16:19:38

定义网络每层神经元的数量，通过Xavier均匀分布初始化网络。代码实现如下：

1
2
3
4
5
6
7
8
9
10
paddle.seed(0)

# 指定激活函数
activate_fn = paddle.nn.Tanh
# 指定参数初始化方式
init_fn_name = 'uniform'

model = MLP(layers_size, init_fn_name, init_fn=xavier_uniform_r, act_fn=activate_fn)
inputs = paddle.normal(shape=[1, 100], std=0.1)
y = model(inputs)
1
2
运行时长: 11毫秒
结束时间: 2022-12-24 16:20:26

打印每层神经元输出的方差，观察每层的方差值。

1
2
for i in range(len(model.z) - 1):
    print('layer %d: , %f'%(i, model.z[i].numpy().var()))
1
2
3
4
layer 0: , 0.005596
layer 1: , 0.003397
layer 2: , 0.004084
layer 3: , 0.005171
[√] 7.4.2.3 观察模型训练收敛性

为了进一步验证Xavier初始化的效果，我们在一个简单的二分类任务上来训练MLP模型，并观察模型收敛情况。

构建数据集 这里使用在第3.1.1中定义的make_moons函数构建一个简单的二分类数据集。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from nndl import make_moons

class MoonsDataset(io.Dataset):
    def __init__(self, mode='train', num_samples=300, num_train=200):
        super(MoonsDataset, self).__init__()
        X, y = make_moons(n_samples=num_samples, shuffle=True, noise=0.5)
        if mode == 'train':
            self.X, self.y = X[:num_train], y[:num_train]
        else:
            self.X, self.y = X[num_train:], y[num_train:]

    def __getitem__(self, idx):
        return self.X[idx], self.y[idx]

    def __len__(self):
        return len(self.y)
1
2
运行时长: 6毫秒
结束时间: 2022-12-24 16:22:13

创建训练和验证集，构建DataLoader。代码实现如下：

1
2
3
4
5
paddle.seed(0)
train_dataset = MoonsDataset(mode='train')
dev_dataset = MoonsDataset(mode='dev')
train_loader = io.DataLoader(train_dataset, batch_size=10, shuffle=True)
dev_loader = io.DataLoader(dev_dataset, batch_size=10, shuffle=True)
1
2
运行时长: 890毫秒
结束时间: 2022-12-24 16:22:59

定义五层MLP，分别以Xavier初始化和标准高斯分布初始化方式对网络进行初始化，训练100回合，对比两个模型的训练损失变化情况。代码实现如下：

alec：

  • Xavier高斯分布初始化 和 标准高斯分布初始化 的参数分布都是高斯分布的，但是Xavier高斯分布初始化的方差是由网络结构中的神经元的数量决定的，标准高斯分布初始化是固定的自定义均值和方差。一个和网络结构耦合，一个和网络结构无关。
  • SGD优化器的参数，只有一个学习率，是最基本的优化器。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import nndl

paddle.seed(0)
np.random.seed(0)

# 定义网络每层神经元的数量
layers_size = [2, 300, 500, 700, 400, 1]
# 指定激活函数
activate_fn = paddle.nn.Tanh

# 指定参数初始化方式为Xavier高斯分布初始化
init_fn_name = 'normal'
model1 = MLP(layers_size, init_fn_name, init_fn=xavier_normal_std, act_fn=activate_fn)
opt1 = optimizer.SGD(learning_rate=0.005, parameters=model1.parameters())
loss_fn = F.binary_cross_entropy_with_logits
m = nndl.Accuracy(is_logist=True)
runner1 = RunnerV3(model1, opt1, loss_fn, m)
runner1.train(train_loader, dev_loader, num_epochs=100, eval_steps=400, log_steps=0)

# 指定参数初始化方式为N(0, 1)高斯分布初始化
init_fn_name = 'basic'
model2 = MLP(layers_size, init_fn_name, None, act_fn=activate_fn)
opt2 = optimizer.SGD(learning_rate=0.005, parameters=model2.parameters())
runner2 = RunnerV3(model2, opt2, loss_fn, m)
runner2.train(train_loader, dev_loader, num_epochs=100, eval_steps=400, log_steps=0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
[Evaluate]  dev score: 0.81000, dev loss: 0.42877
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.81000
[Evaluate]  dev score: 0.83000, dev loss: 0.42839
[Evaluate] best accuracy performence has been updated: 0.81000 --> 0.83000
[Evaluate]  dev score: 0.83000, dev loss: 0.42997
[Evaluate]  dev score: 0.83000, dev loss: 0.42962
[Evaluate]  dev score: 0.83000, dev loss: 0.42941
[Train] Training done!
[Evaluate]  dev score: 0.75000, dev loss: 3.23409
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.75000
[Evaluate]  dev score: 0.72000, dev loss: 3.07022
[Evaluate]  dev score: 0.70000, dev loss: 3.35328
[Evaluate]  dev score: 0.75000, dev loss: 2.08153
[Evaluate]  dev score: 0.73000, dev loss: 2.73204
[Train] Training done!
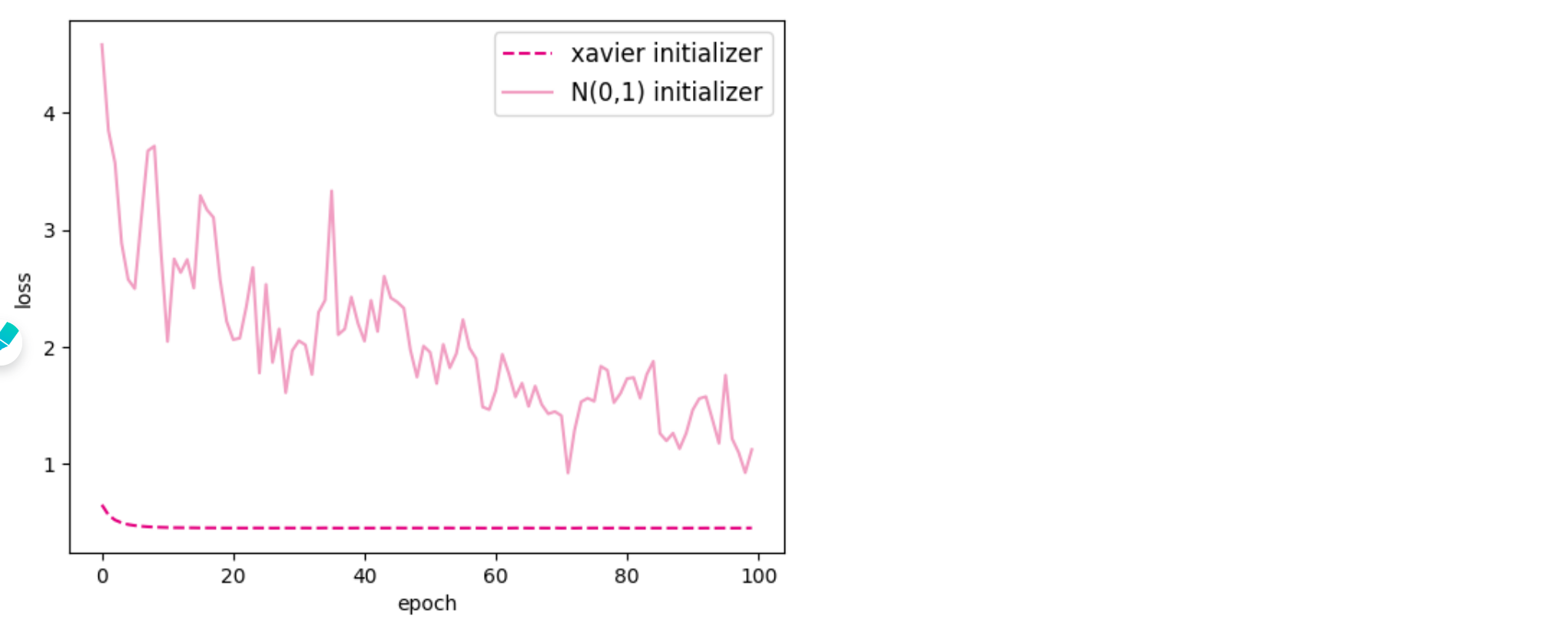
1
2
3
4
5
6
7
8
fig, ax = plt.subplots()
plt.plot(runner1.train_epoch_losses, label='xavier initializer', c='#e4007f', linestyle='--')
plt.plot(runner2.train_epoch_losses, label='N(0,1) initializer', c='#f19ec2')
ax.set_xlabel('epoch')
ax.set_ylabel('loss')
plt.legend(fontsize='large')
plt.savefig('opti-xavier.pdf')
plt.show()

image-20221224162933545

alec：

  • 从输出结果看，使用基于网络结构数量进行方差缩放的Xavier初始化，模型的损失相对较小，模型效果更好。

[√] 7.5 逐层规范化

alec：

  • 逐层规范化（Layer-wise Normalization）是将传统机器学习中的数据规范化方法应用到深度神经网络中
  • 对神经网络中隐藏层的输入进行规范化，从而使得网络更容易训练。
  • （规范化是将隐藏层的输入和输出进行规范化，从而使得网络训练更加容易）
  • 在DNN中，如果一个神经层的输入数据的分布状况发生了变化，从机器学习的角度来看，这个网络的之前学习的参数无效，需要重新学习。这叫内部协变量偏移。为了解决这个问题，那么就在训练之前，就设置一定的方法，让神经网络中每层的输入都是符合某种稳定分布的规划数据。这个动作叫做规范化。需要对每一层都进行输入数据的规范化，这个动作加逐层规范化。

逐层规范化（Layer-wise Normalization）是将传统机器学习中的数据规范化方法应用到深度神经网络中，对神经网络中隐藏层的输入进行规范化，从而使得网络更容易训练。

在深度神经网络中，一个神经层的输入是之前神经层的输出。给定一个神经层$l$，它之前的神经层$(1, \cdots, l-1$)的参数变化会导致其输入的分布发生较大的改变。从机器学习角度来看，如果一个神经层的输入分布发生了改变，那么其参数需要重新学习，这种现象叫作内部协变量偏移（Internal Covariate Shift）。 为了缓解这个问题，我们可以对每一个神经层的输入进行规范化操作，使其分布保持稳定。

[√] 7.5.1 批量规范化

alec：

  • 对于一个深度神经网络，为了提高优化效率，要使第$l$层的净输入$z^{(l)}$的分布一致，比如都规范化到标准正态分布。

  • 实际中，一般在线性层和激活函数之间使用规范化操作。

  • 只有分布统一的数据，才能训练处有效的网络参数，因此需要对每一层的数据先规范化，然后再训练。

  • 而为了提高规范化效率，一般使用标准化将净输入$z^{(l)}$的每一维都规范化到标准正态分布。

  • $$
    \hat{z}^{(l)} = \frac{z^{(l)} - \mu_{\mathcal B}}{\sqrt{\sigma_{\mathcal B}^2 + \epsilon}},
    $$
    其中$\mu_{\mathcal B}$、$ \sigma_{\mathcal B}^2$为小批量样本的均值和方差。

  • 使用小批量样本的均值和方差来规范化数据，使得数据符合标准正态分布。

  • 对净输入$ z^{(l)}$的标准规范化会使得其取值集中到0附近，如果使用Sigmoid型激活函数时，这个取值区间刚好是接近线性变换的区间，减弱了神经网络的非线性性质。这样就导致激活函数的非线性作用微弱了，导致网络的表示能力减弱。

  • 因此，为了使得规范化不对网络的表示能力造成负面影响，可以通过一个附加的缩放和平移变换改变取值区间。则有：

    • $$
      \hat{\ z}^{(l)} \triangleq BN_{ \gamma, v \beta}( z^{(l)}) = \frac{ z^{(l)} - \mu_{\mathcal B}}{\sqrt{ \sigma_{\mathcal B}^2 + \epsilon}} \odot \gamma + \beta.
      $$

    • 右边的γ和β是用来进行缩放和平移的，让规范化之后的数据远离0附近。

  • 上面的这种规划化操作，叫做批量规范化，即BatchNorm，BN层，通常在线性层和激活层之间，目的是统一每层输入数据的分布，从而使得网络训练出来的参数有效。

  • 其中，指定的γ和β是数据最终规划化之后的均值和方差。

[√] 7.5.1.1 BatchNorm算子

下面定义BatchNorm算子，实现批量规范化。

alec：

  • 在实现批量规范化时，在训练过程中的均值和方差可以动态计算，但在测试时需要保存固定，否则模型输出就会受到同一批次中其他样本的影响。

因此，在训练时需要将每一批次样本的均值和方差以移动平均值的方式记录下来，预测时使用整个训练集上的均值和方差（也就是保存的移动平均值）进行规范化。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class BatchNorm(nn.Layer):
    def __init__(self, num_features, eps=1e-7, momentum=0.9, gamma=1.0, beta=0.0):
        """
        批量规范化初始化
        输入:
            - num_features: 输入特征数
            - eps: 保持数值稳定性而设置的常数
            - momentum: 用于计算移动平均值
            - gamma: 缩放的参数
            - beta: 平移的参数
        """
        super(BatchNorm, self).__init__()
        shape = (1, num_features)
        self.gamma = paddle.to_tensor(gamma, dtype='float32')
        self.beta = paddle.to_tensor(beta, dtype='float32')
        self.moving_mean = paddle.zeros(shape)
        self.moving_variance = paddle.ones(shape)
        self.eps = eps
        self.momentum = momentum

    def __call__(self, X, train_mode=True):
        return self.forward(X, train_mode)

    def forward(self, X, train_mode=True):
        if not train_mode:
            X = (X - self.moving_mean) / paddle.sqrt(self.moving_variance + self.eps)
        else:
            assert len(X.shape) in (2, 4)
            # alec：线性层，只有两个维度
            if len(X.shape) == 2:
                # 对于Linear层
                # alec：计算当前批次数据的均值和方差
                mean = paddle.mean(X, axis=0)
                var = ((X - mean) ** 2).mean(axis=0)
            # alec：卷积层，有三个或四个维度
            else:
                # 对于卷积层
                # alec：计算当前批次数据的均值和方差
                mean = paddle.mean(X, axis=[0, 2, 3], keepdim=True)
                var = ((X - mean) ** 2).mean(axis=[0, 2, 3], keepdim=True)
            # alec：进行当前批次数据的规范化
            X = (X - mean) / paddle.sqrt(var, self.eps)
            # 保存均值和方差的移动平均值
            self.moving_mean = self.momentum * self.moving_mean + (1. - self.momentum) * mean
            self.moving_variance = self.momentum * self.moving_variance + (1. - self.momentum) * var
        # 缩放和平移
        y = self.gamma * X + self.beta
        return y
1
2
运行时长: 10毫秒
结束时间: 2022-12-24 17:30:55

alec：

  • BN的过程，就是计算当前批次数据的均值和方差，然后进行规范化操作，同时记录均值和方差的移动平均值，并进行缩放和移动来防止规范化后的数据落在0周围导致激活函数的非线性作用减弱进而导致网络的表示能力减弱
[√] 7.5.1.2 支持逐层规范化的MLP算子

重新定义MLP算子，加入逐层规范化功能。初始化网络时新增三个参数：norm_name指定使用哪一种逐层规范化（默认为None）、gamma和beta为缩放和平移变换的参数。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class MLP(nn.Layer):
    def __init__(self, layers_size, init_fn_name, init_fn, act_fn, norm_name=None, gamma=None, beta=None):
        """
        多层网络初始化
        输入：
            - layers_size: 每层神经元的数量
            - init_fn_name: 网络中参数初始化方法
            - init_fn: 计算高斯分布标准差或均匀分布r值
            - act_fn: 激活函数
            - norm_name: 使用哪一种逐层规范化
            - gamma、beta: 缩放和平移变换的参数
        """
        super(MLP, self).__init__()
        self.linear = paddle.nn.Sequential()
        self.normalization = {}
        self.num_layers = len(layers_size) - 1
        for i in range(self.num_layers):
            input_size, output_size = layers_size[i], layers_size[i + 1]
            # alec：根据当前层神经元的数量进行参数初始化
            if init_fn_name == 'normal':
                # Xavier高斯分布初始化，计算方差
                self.linear.add_sublayer(str(i), nn.Linear(input_size, output_size,
                                           weight_attr=nn.initializer.Normal(mean=0, std=init_fn(input_size, output_size))))
            elif init_fn_name == 'uniform':
                r = init_fn(input_size, output_size)
                self.linear.add_sublayer(str(i), nn.Linear(input_size, output_size, weight_attr=nn.initializer.Uniform(low=-r, high=r)))
            else:
            # alec：都不是的话，则使用一般的固定值初始化参数
                self.linear.add_sublayer(str(i), nn.Linear(input_size, output_size, weight_attr=nn.initializer.Normal()))
            # 判断是否使用逐层规范化，以及使用哪一种逐层规范化
            if norm_name == 'bn':
                self.normalization[i] = BatchNorm(output_size, gamma=gamma[i], beta=beta[i])
            elif norm_name == 'ln':
             # LayerNorm：对一个中间层的所有神经元进行规范化
                self.normalization[i] = LayerNorm(gamma=gamma[i], beta=beta[i])
        self.act_fn = act_fn()
        self.norm_name = norm_name
        self.z = {}

    def __call__(self, X, train_mode=True):
        return self.forward(X, train_mode)

    def forward(self, X, train_mode=True):
        y = X
        for num_layer in range(self.num_layers):
            y = self.linear[num_layer](y)
            if num_layer != self.num_layers - 1:
                # alec：先通过线性层，然后进行BN，最后通过激活函数
                if self.norm_name == 'bn':
                    y = self.normalization[num_layer](y, train_mode)
                elif self.norm_name == 'ln':
                    y = self.normalization[num_layer](y)
                # 为了展示逐层规范化后的输出的均值和方差，使用z[num_layer]进行记录
                self.z[num_layer] = y
                y = self.act_fn(y)
        return y
1
2
运行时长: 13毫秒
结束时间: 2022-12-24 17:41:15

alec：

  • 为批量规范化是对一个中间层的单个神经元进行规范化操作
  • 批量规范化的时候，小批量样本的数量不能太小，否则难以计算单个神经元的统计信息

因为批量规范化是对一个中间层的单个神经元进行规范化操作，所以要求小批量样本的数量不能太小，否则难以计算单个神经元的统计信息。所以我们使用paddle.randn随机生成一组形状为(200, 100)的数据, 打印数据送入网络前的均值与标准差。再分别定义使用批量规范化和不使用批量规范化的五层线性网络，分别打印网络第四层的均值与标准差，对比结果。

[√] 7.5.1.3 内部协变量偏移实验

alec：

  • 内部协变量偏移实验，其实就是指的数据进行批量规范化和没有进行批量规范化的区别和影响。

下面我们构建两个模型：model1不使用批量规范化，model2使用批量规范化，观察批量规范化是否可以缓解内部协变量偏移问题。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
paddle.seed(0)

# 定义网络每层神经元的数量
layers_size = [100, 200, 400, 300, 2, 2]

data = paddle.randn(shape=[200, 100])
print('data mean: ', data.numpy().mean())
print('data std: ', data.numpy().std())

activate_fn = paddle.nn.Tanh
model1 = MLP(layers_size, 'basic', None, act_fn=activate_fn)
output = model1(data)
print('no batch normalization: ')
print('model output mean: ', model1.z[3].numpy().mean(axis=0))
print('model output std:', model1.z[3].numpy().std(axis=0))

gamma = [1, 1, 1, 1, 1]
beta = [0, 0, 0, 0, 0]
model2 = MLP(layers_size, 'basic', None, act_fn=activate_fn, norm_name='bn', gamma=gamma, beta=beta)
output = model2(data)
print('with batch normalization: ')
print('model output mean: ', model2.z[3].numpy().mean(axis=0))
print('model output std:', model2.z[3].numpy().std(axis=0))
1
2
3
4
5
6
7
8
data mean:  0.001138683
data std:  1.0084993
no batch normalization: 
model output mean:  [ 0.6876077 -0.8056189]
model output std: [18.348772 15.487542]
with batch normalization: 
model output mean:  [-4.9173834e-09 -8.0466274e-09]
model output std: [1.0000002 1.       ]

alec：

  • 从输出结果看，在经过多层网络后，网络输出的均值和标准差已经发生偏移。而当我们指定批量规范化的均值和标准差为0,1时，网络输出的均值和标准差就会变为0,1。
  • 当我们指定$\gamma$和$ \beta$时，网络输出的标准差和均值就变为$ \gamma$和$ \beta$的值。
1
2
3
4
5
6
7
8
9
10
11
paddle.seed(0)

gamma = [1, 2, 3, 5, 4]
beta = [3, 2, 1, 2, 2]
model3 = MLP(layers_size, 'basic', None, act_fn=activate_fn, norm_name='bn', gamma=gamma, beta=beta)
output = model3(data)
print('batch normalization with different gamma and beta for different layer: ')
print('output means with bn 0: ', model3.z[0].numpy().mean())
print('output stds with bn 0: ', model3.z[0].numpy().std())
print('output means with bn 3: ', model3.z[3].numpy().mean())
print('output stds with bn 3: ', model3.z[3].numpy().std())

alec：

  • gamma = [1, 2, 3, 5, 4]、beta = [3, 2, 1, 2, 2]，这两个list是用来指定神经网络5层中每一层的均值和方差
1
2
3
4
5
batch normalization with different gamma and beta for different layer: 
output means with bn 0:  3.0
output stds with bn 0:  1.0
output means with bn 3:  2.0
output stds with bn 3:  5.0

alec：

  • 该实验说明，没有进行BN的话，那么数据的分布就会改变；进行了BN，那么每层数据的分布都会按照指定的均值和方差来分布，也就是按照缩放和偏移量进行分布。
  • 因此BN对于数据的分布控制是有效的，从而能够网络高效的进行参数计算。
[√] 7.5.1.4 均值和方差的移动平均计算实验

下面测试批量规范化中训练样本均值和方差的移动平均值计算。使网络前向迭代50个回合，这个前向计算并不涉及网络训练与梯度更新，只是模拟网络训练时批量规范化中训练样本的均值和方差用移动平均计算的过程。代码实现如下：

1
2
3
4
5
6
7
8
9
10
paddle.seed(0)

epochs = 50
for epoch in range(epochs):
    inputs = paddle.randn(shape=[200, 100])
    output = model3(data)

# 打印批量规范化中训练样本均值和方差的移动平均值
print('batch norm 3 moving mean: ', model3.normalization[3].moving_mean.numpy())
print('batch norm 3 moving variance: ', model3.normalization[3].moving_variance.numpy())
1
2
batch norm 3 moving mean:  [[-0.63306284  0.17639302]]
batch norm 3 moving variance:  [[149.98349 267.1632 ]]

开启测试模式，使用训练集的移动平均值作为测试集批量规范化的均值和标准差。代码实现如下：

1
2
3
4
paddle.seed(0)

inputs_test = paddle.randn(shape=[5, 100])
output = model3(inputs_test, train_mode=False)
[√] 7.5.1.5 在MNIST数据集上使用带批量规范化的卷积网络

alec：

  • 批量规范化的提出是为了解决内部协方差偏移问题，但后来发现其主要优点是更平滑的优化地形，以及使梯度变得更加稳定，从而提高收敛速度。

为验证批量规范化的有效性，本节使用飞桨API快速搭建一个多层卷积神经网络。在MNIST数据集上，观察使用批量规范化的网络是否相对于没有使用批量规范化的网络收敛速度更快。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from paddle.nn import Conv2D, MaxPool2D, Linear, BatchNorm2D

# 多层卷积神经网络实现
class MultiConvLayerNet(nn.Layer):
    def __init__(self, use_bn=False):
        super(MultiConvLayerNet, self).__init__()

        # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
        self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
        # 定义汇聚层，窗口的大小为2，步长为2
        self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
        # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
        self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
        # 定义汇聚层，窗口的大小为2，步长为2
        self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
        # 定义一层全连接层，输出维度是10
        self.fc = Linear(980, 10)
        if use_bn:
            # 定义批量规范化层
            # alec：批量规范化层，参数为通道的数量
            self.batch_norm1 = BatchNorm2D(num_features=20)
            self.batch_norm2 = BatchNorm2D(num_features=20)
        self.use_bn = use_bn

    # 定义网络前向计算过程
    def forward(self, inputs):
        # 卷积、BN、ReLU、汇聚、卷积、BN、ReLU、汇聚、reshape、fc
        x = self.conv1(inputs)
        if self.use_bn:
            x = self.batch_norm1(x)
        x = F.relu(x)
        x = self.max_pool1(x)
        x = self.conv2(x)
        if self.use_bn:
            x = self.batch_norm2(x)
        x = F.relu(x)
        x = self.max_pool2(x)
        x = paddle.reshape(x, [x.shape[0], 980])
        x = self.fc(x)
        return x
1
2
运行时长: 8毫秒
结束时间: 2022-12-24 21:12:17

实例化网络并进行训练。model1不使用批量规范化，model2使用批量规范化。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from nndl import Accuracy

paddle.seed(0)
# 确保从paddle.vision.datasets.MNIST中加载的图像数据是np.ndarray类型
paddle.vision.image.set_image_backend('cv2')

# 使用MNIST数据集
train_dataset = MNIST(mode='train', transform=transform)
train_loader = io.DataLoader(train_dataset, batch_size=64, shuffle=True)
dev_dataset = MNIST(mode='test', transform=transform)
dev_loader = io.DataLoader(train_dataset, batch_size=64)
model1 = MultiConvLayerNet(use_bn=False)
opt1 = paddle.optimizer.Adam(learning_rate=0.01, parameters=model1.parameters())
loss_fn = F.cross_entropy
metric = Accuracy()
runner1 = RunnerV3(model1, opt1, loss_fn, metric)
print('train network without batch normalization')
runner1.train(train_loader, dev_loader, num_epochs=5, log_steps=0, eval_steps=300)

model2 = MultiConvLayerNet(use_bn=True)
opt2 = paddle.optimizer.Adam(learning_rate=0.01, parameters=model2.parameters())
runner2 = RunnerV3(model2, opt2, loss_fn, metric)
print('train network with batch normalization')
runner2.train(train_loader, dev_loader, num_epochs=5, log_steps=0, eval_steps=300)

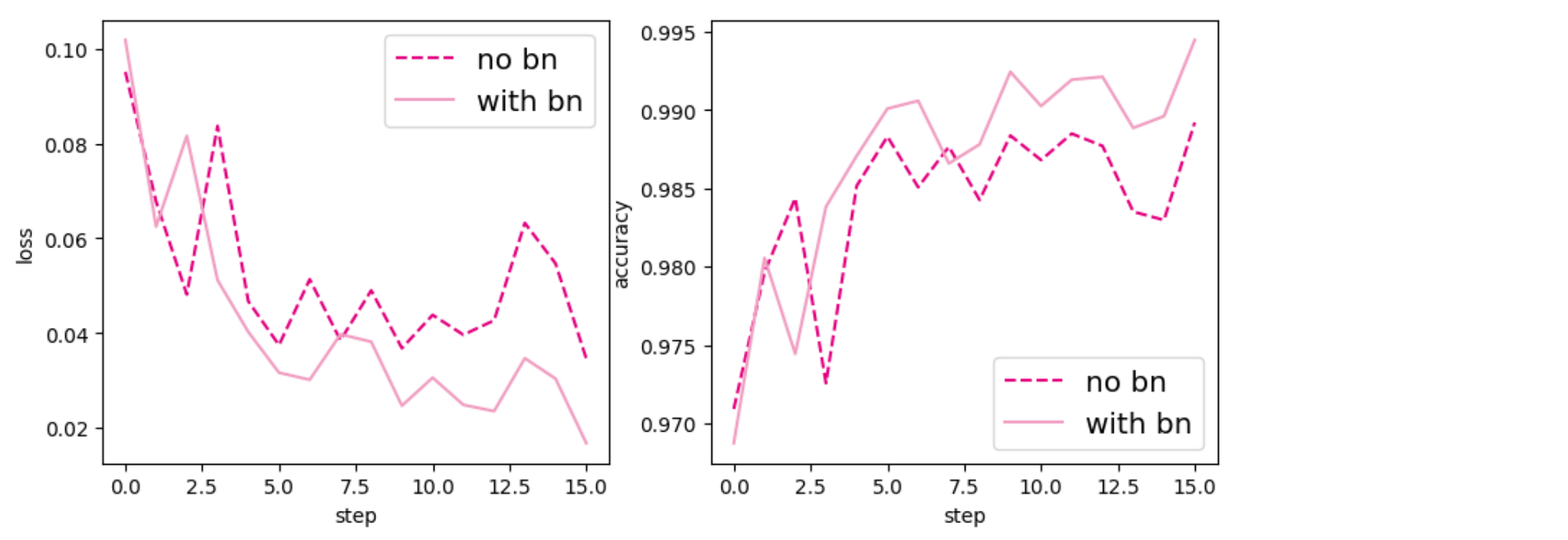
对比model1和model2在验证集上损失和准确率的变化情况。从输出结果看，使用批量规范化的网络收敛速度会更好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
plt.figure(figsize=(10, 4))
ax1 = plt.subplot(121)
ax1.plot(np.array(runner1.dev_losses)[:, 1], label='no bn', c='#e4007f', linestyle='--')
ax1.plot(np.array(runner2.dev_losses)[:, 1], label='with bn', c='#f19ec2')
ax1.set_xlabel('step')
ax1.set_ylabel('loss')
plt.legend(fontsize='x-large')
ax2 = plt.subplot(122)
ax2.plot(runner1.dev_scores, label='no bn', c='#e4007f', linestyle='--')
ax2.plot(runner2.dev_scores, label='with bn', c='#f19ec2')
ax2.set_xlabel('step')
ax2.set_ylabel('accuracy')
plt.legend(fontsize='x-large')
plt.savefig('opti-acc.pdf')
plt.show()

image-20221224212956409

alec：

  • 可以看出，使用批量规范化的模型收敛速度和效果会更好

[√] 7.5.2 层规范化

alec：

  • 层规范化（Layer Normalization）和批量规范化是非常类似的方法
  • 它们的区别在于批量规范化对中间层的单个神经元进行规范化操作，而层规范化对一个中间层的所有神经元进行规范化

层规范化定义为
$$
\begin{aligned}
\hat{ z}^{(l)} &= \frac{ z^{(l)} - \mu^{(l)}}{\sqrt{\sigma^{(l)^2} + \epsilon}} \odot \gamma + \beta, \
&\triangleq LN_{ \gamma, \beta}( z^{(l)}),
\end{aligned}
$$

其中$ z^{(l)}$为第$l$层神经元的净输入， $ \gamma$和$ \beta$分别代表缩放和平移的参数向量，和$ z^{(l)}$维数相同。$\mu^{(l)}$和$\sigma^{(l)^2}$分别为$ z^{(l)}$的均值和方差。

根据上面的公式可以看出，对于$K$个样本的一个小批量合集$z^{(l)} = [ z^{(1, l)}; …; z^{(K, l)}]$，层规范化是对矩阵$ z^{(l)}$的每一列进行规范化，而批量规范化是对每一行进行规范化。一般而言，批量规范化是一种更好的选择。当小批量样本数量比较小时，可以选择层规范化。

一般而言，批量规范化是一种更好的选择

[√] 7.5.2.1 LayerNorm算子

定义LayerNorm实现层规范化算子。与批量规范化不同，层规范化对每个样本的所有特征进行规范化。代码实现如下：

alec：

  • 批规范化对一个batch的样本，对相同的一个特征进行规范化
  • 层规范化，对单个样本，所有的通道特征进行规范化
1
2
3
4
5
6
7
8
9
# 层规范化
# axis=[1, 2, 3] 就表示对一个图像的所有的特征进行规范化，而不是对多个图像的单个特征进行规范化
            mean = paddle.mean(X, axis=[1, 2, 3], keepdim=True)
            var = ((X - mean) ** 2).mean(axis=[1, 2, 3], keepdim=True)

# 批规范化
# axis=[0, 2, 3] 就表示对一批图像的单个特征图进行规范化
        mean = paddle.mean(X, axis=[0, 2, 3], keepdim=True)
        var = ((X - mean) ** 2).mean(axis=[0, 2, 3], keepdim=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class LayerNorm(nn.Layer):
    def __init__(self, eps=1e-7,  gamma=1.0, beta=0.0):
        """
        层规范化初始化
        输入:
            - eps: 保持数值稳定性而设置的常数
            - gamma: 缩放的参数
            - beta: 平移的参数
        """
        super().__init__(self.__class__.__name__)
        self.gamma = paddle.to_tensor(gamma, dtype='float32')
        self.beta = paddle.to_tensor(beta, dtype='float32')
        self.eps = eps

    def forward(self, X):
        # 层规范化对每个样本的每个特征进行规范化
        assert len(X.shape) in (2, 3, 4)
        if len(X.shape) == 4:
            # axis=[1, 2, 3] 就表示对一个图像的所有的特征进行规范化，而不是对多个图像的单个特征进行规范化
            mean = paddle.mean(X, axis=[1, 2, 3], keepdim=True)
            var = ((X - mean) ** 2).mean(axis=[1, 2, 3], keepdim=True)
        else:#全连接的话，直接对第二维进行均值和方差求值
            mean = paddle.mean(X, axis=-1, keepdim=True)
            var = ((X - mean) ** 2).mean(axis=-1, keepdim=True)
        X = (X - mean) / paddle.sqrt(var, self.eps)# 规范化
        y = self.gamma * X + self.beta# 缩放和平移
        return y
[√] 7.5.2.2 层规范化的验证实验

随机初始化一组形状为（10，100）的数据，输入带有层规范化的前馈神经网络中，得到网络输出并打印输出的标准差和均值。指定$ \gamma$和$ \beta$，从输出结果看，网络输出的标准差和均值变为$ \gamma$和$ \beta$的值。代码实现如下：

alec：

  • bn是批量规范化、ln是层规范化，bn是在单个特征图、一批图像上规范化、ln是在单个图像、一层的特征图上做规范化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
paddle.seed(0)

# 定义网络每层神经元的数量
layers_size = [100, 200, 400, 300, 2, 2]

# 随机生成数据
data = paddle.randn(shape=[10, 100])
activate_fn = paddle.nn.Tanh
gamma = [1, 2, 3, 5, 4]
beta = [3, 2, 1, 2, 2]
model = MLP(layers_size, 'basic', None, act_fn=activate_fn, norm_name='ln', gamma=gamma, beta=beta)
output = model(data)
print('layer normalization with different gamma and beta for different layer: ')
print('output means with ln 0: ', model.z[0].numpy().mean(axis=-1))
print('output stds with ln 0: ', model.z[0].numpy().std(axis=-1))
print('output means with ln 1: ', model.z[3].numpy().mean(axis=-1))
print('output stds with ln 1: ', model.z[3].numpy().std(axis=-1))

因为层规范化是对每个样本的每个通道做规范化，不需要存储训练数据的均值和方差的移动平均值，所以这里不需要多轮迭代累计移动平均值再做测试。而随机生成测试数据经过带层规范化的神经网络和上述代码实现方式相同，这里不再重复展示。

深度学习技术栈 > 深度学习 > 实践学习 > 神经网络与深度学习：案例与实践 - 飞桨 - 邱锡鹏
7 - 网络优化与正则化 - 书籍2
https://alec-97.github.io/posts/2864444717/
作者
Shuai Zhao
发布于
2022年12月25日
许可协议