3 - 线性分类

本文最后更新于：3 个月前

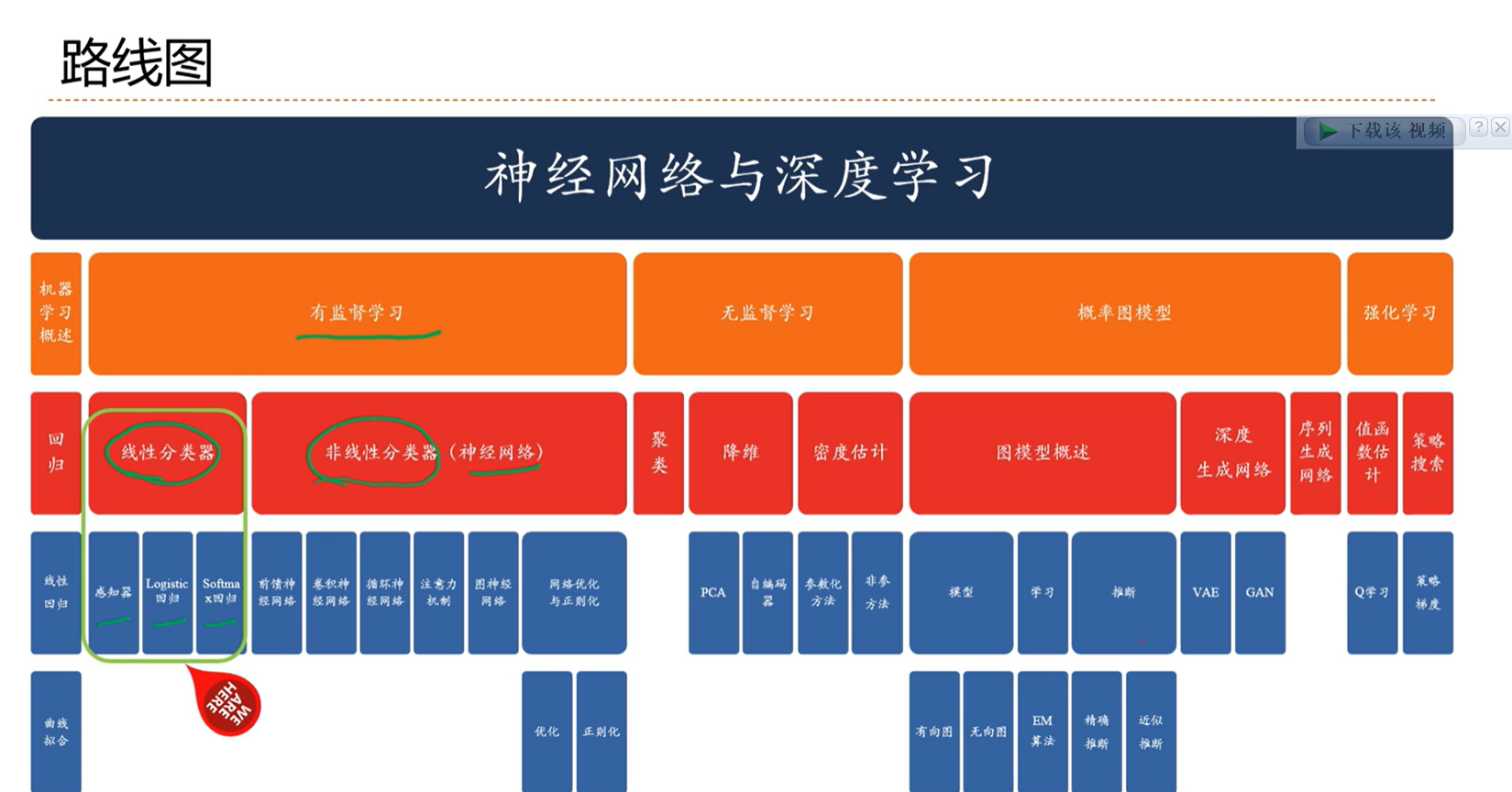
3 - 课节3: 线性分类

3.0 - 线性模型概述

image-20221208180014930

image-20221208180106694

3.1 - 分类问题示例

image-20221208180322450

image-20221208180504177

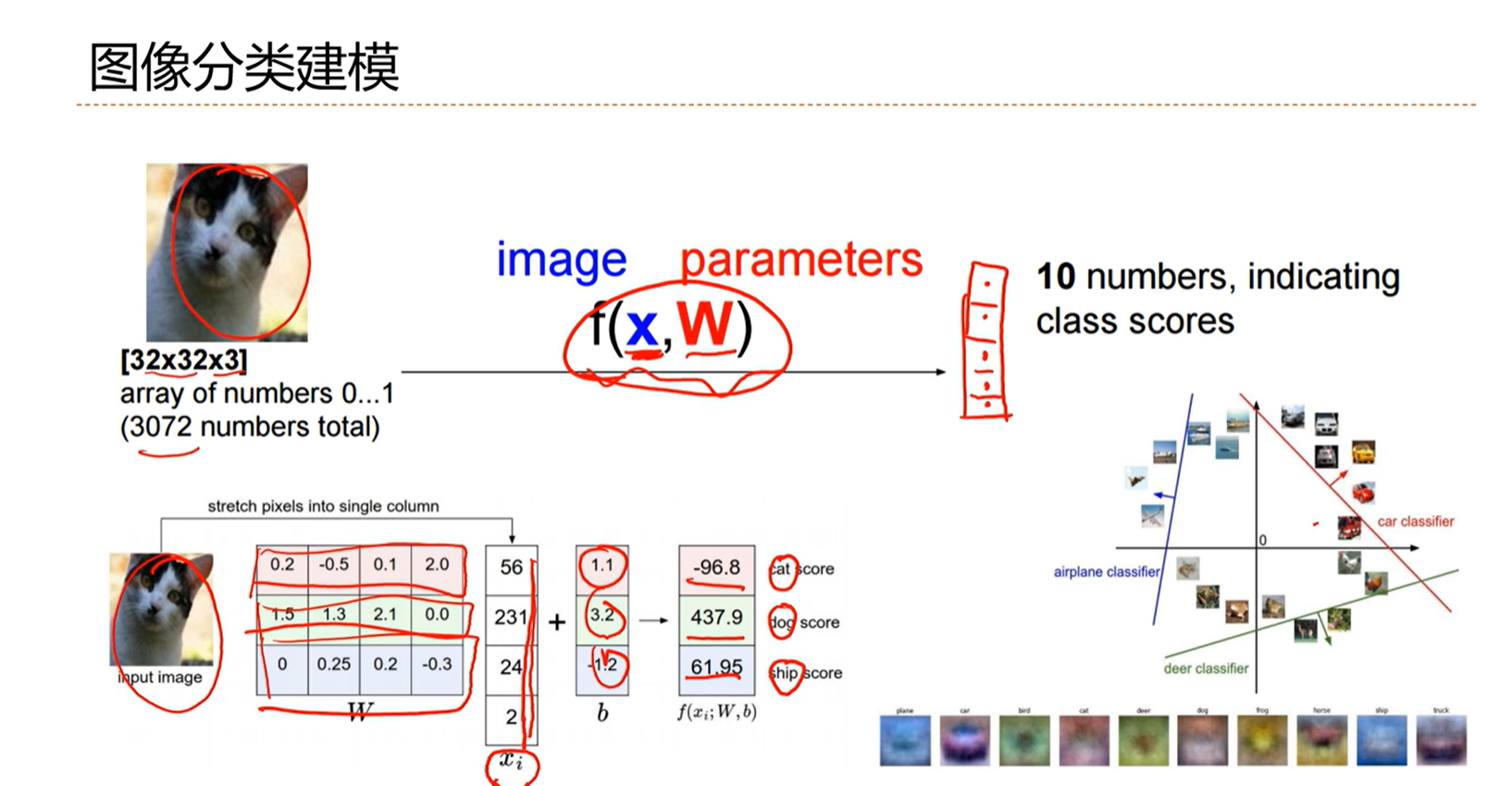
image-20221208180801488

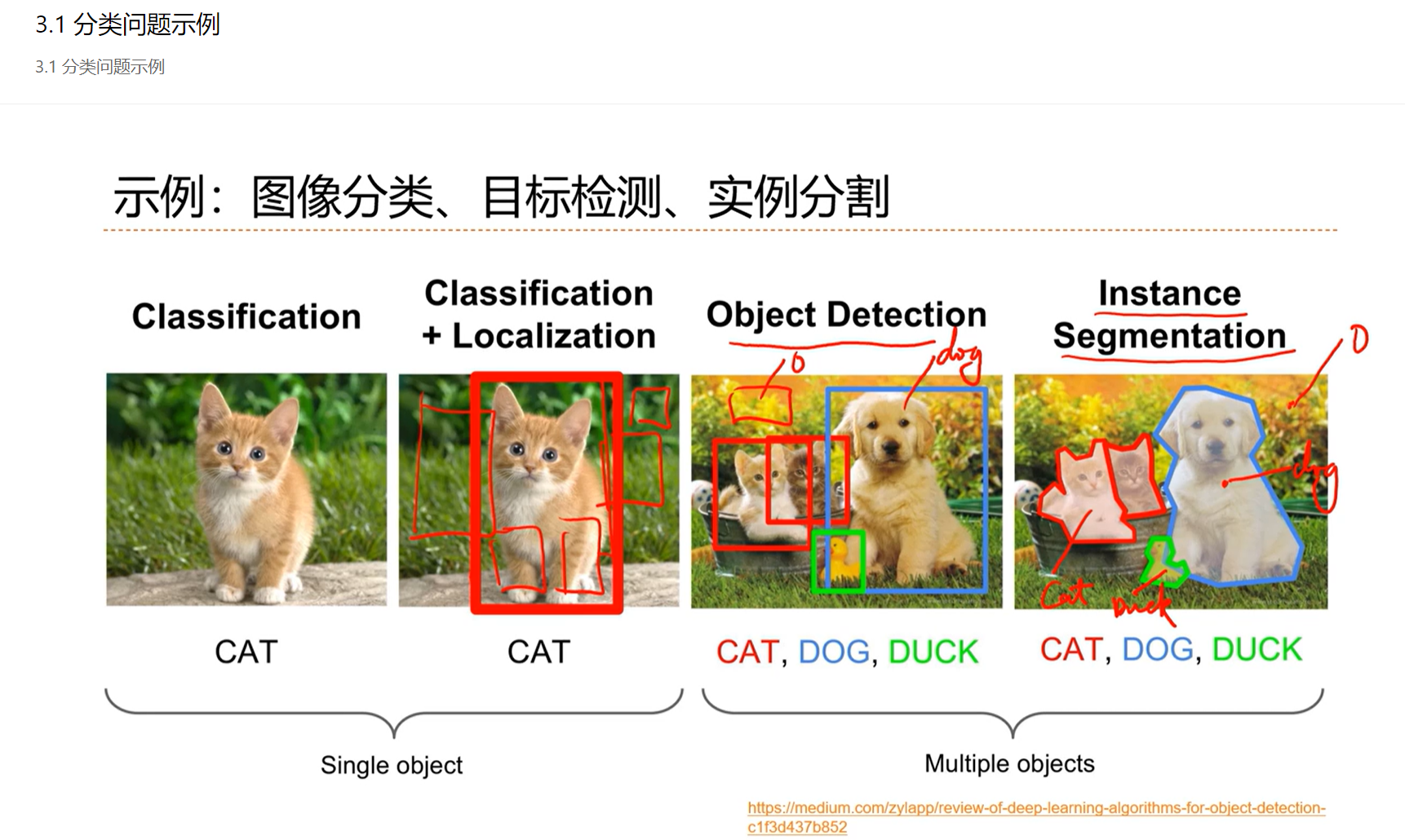
image-20221208181224143

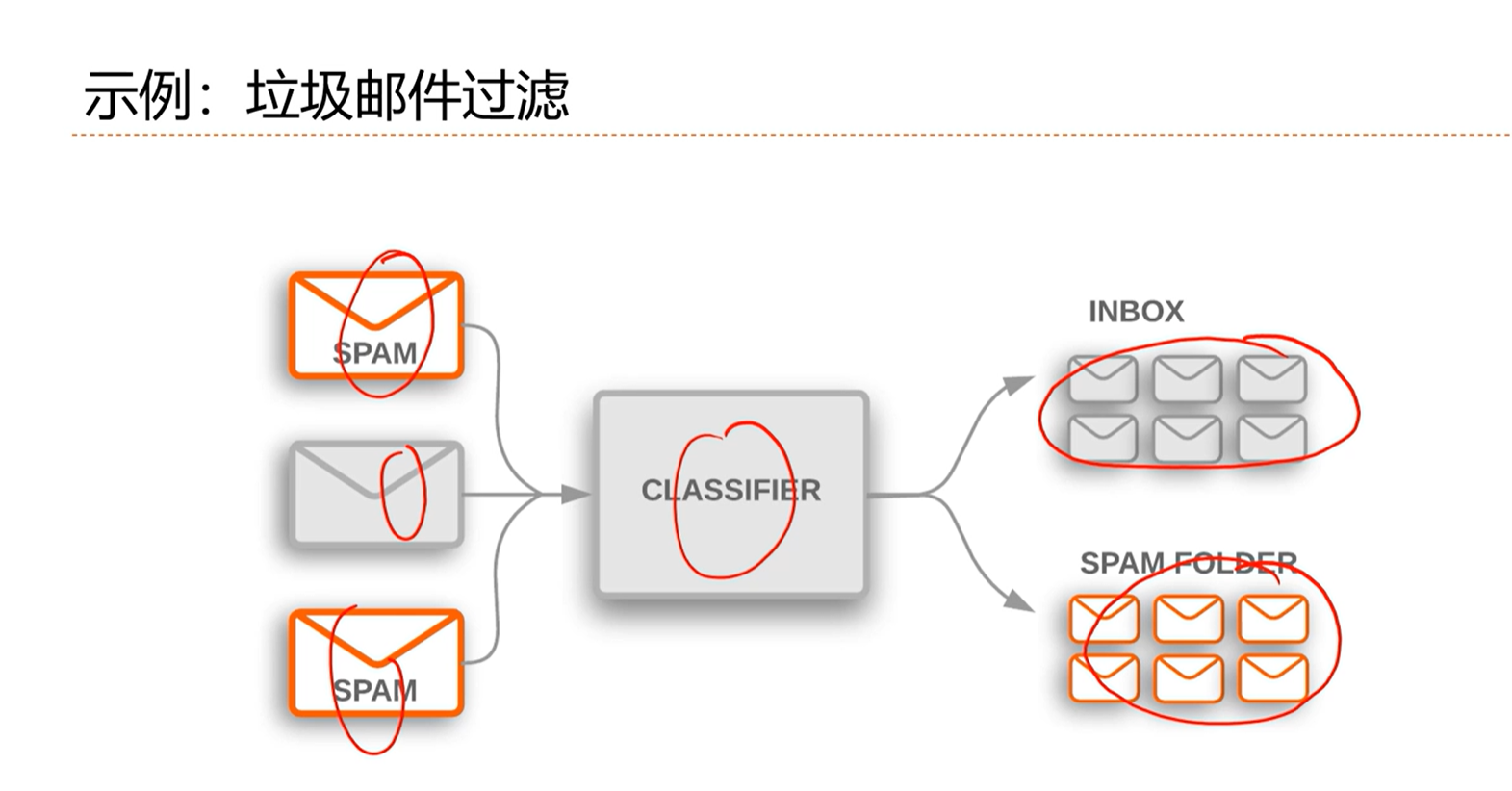
image-20221208181333389

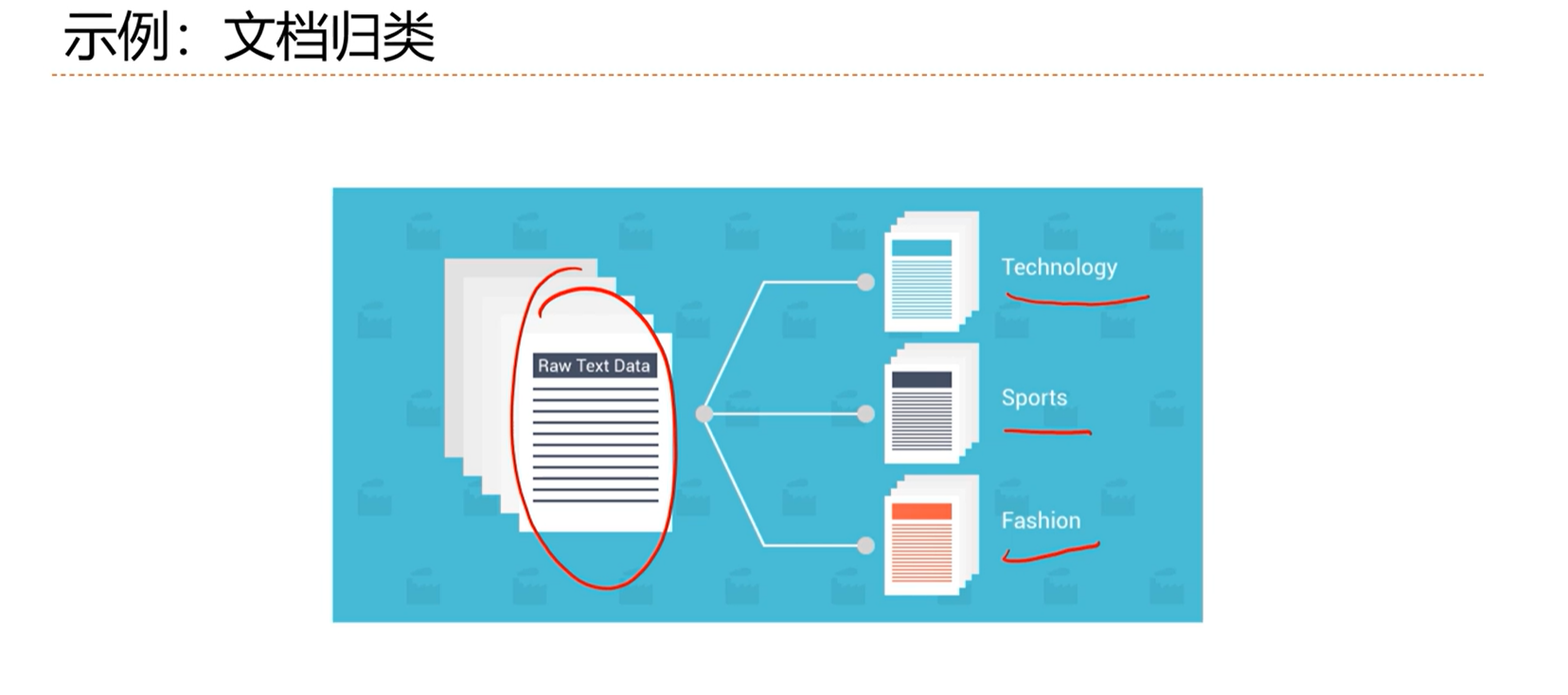
image-20221208181420194

image-20221208181501060

image-20221208182020884

这种方式的缺点在于将文本的语序信息丢掉了

3.2 - 线性分类模型

image-20221208212705641

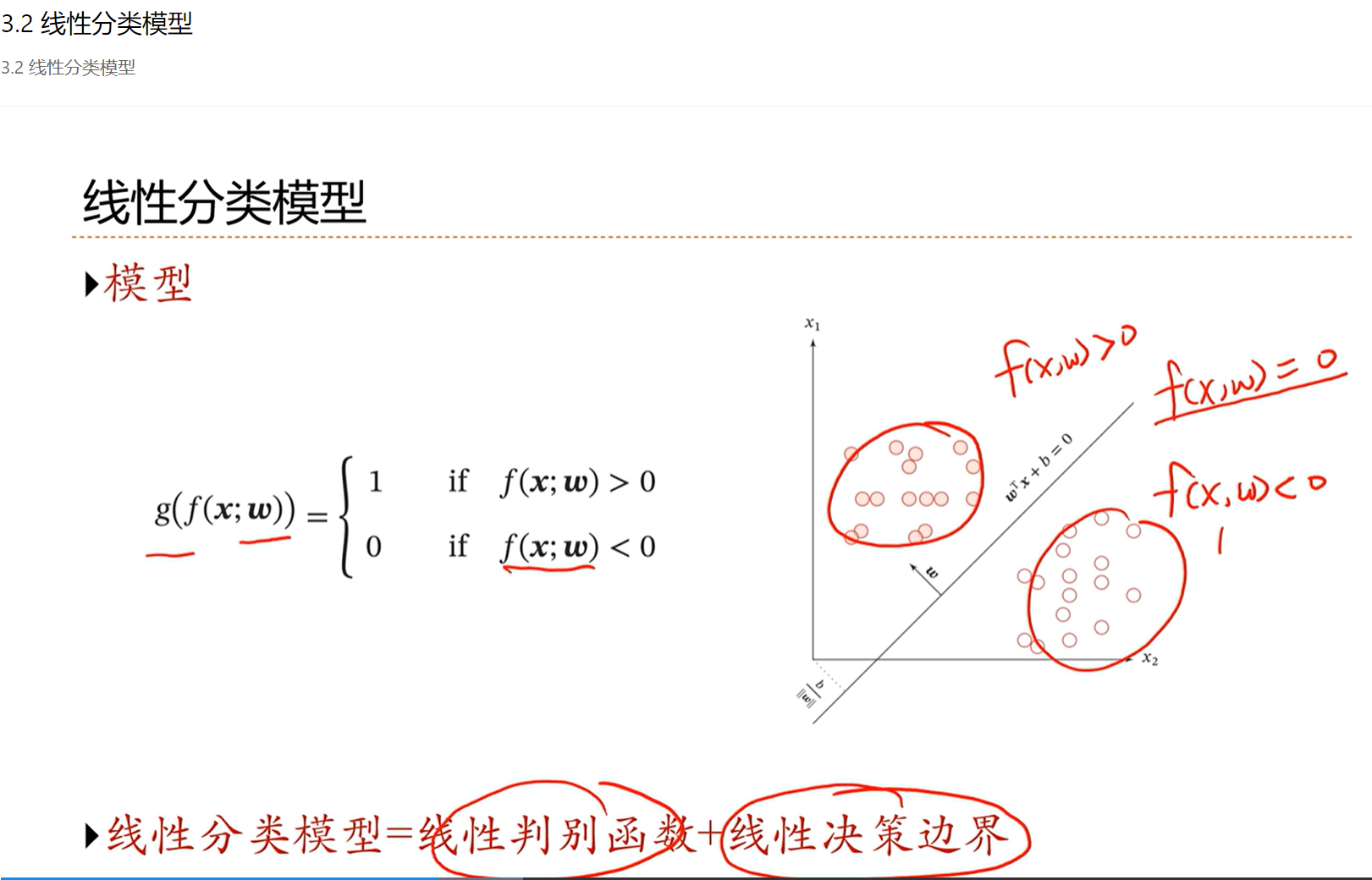
image-20221208212946373

image-20221208213134894

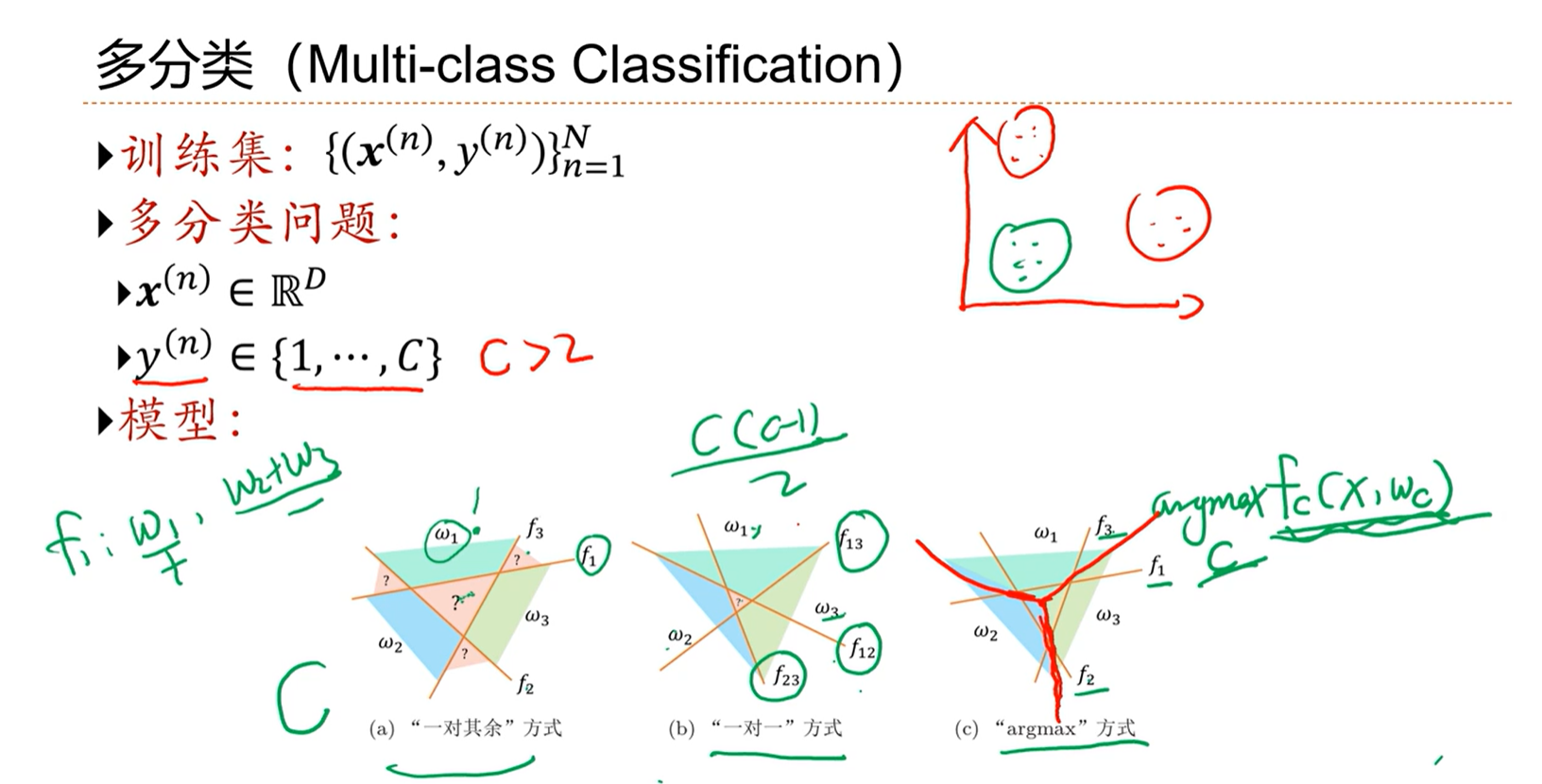
image-20221208214229031

分类问题因为y不可导，因此要寻找更优的损失函数

3.3 - 交叉熵与对数似然

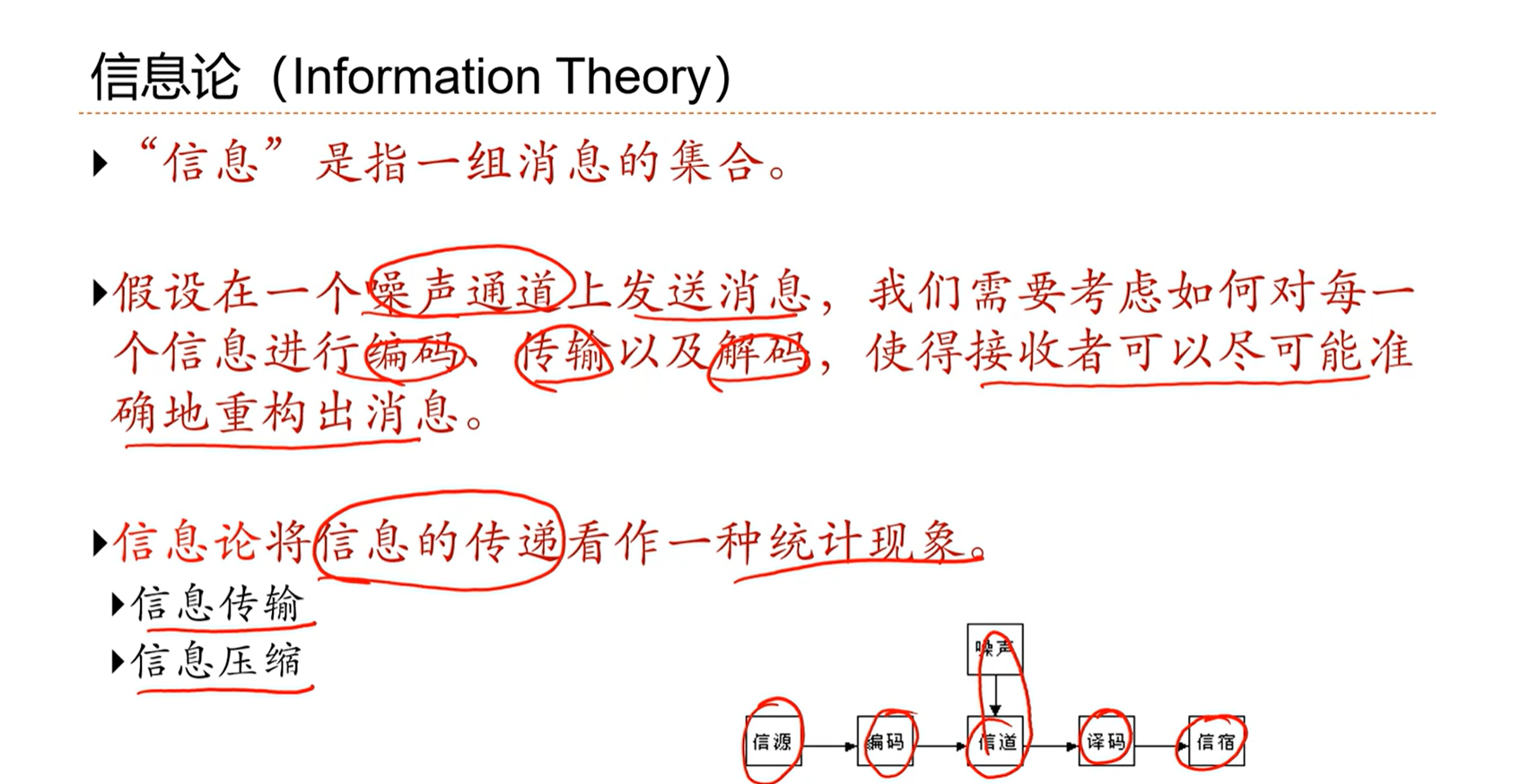
image-20221208214634724

image-20221208215313851

image-20221208215907378

交叉熵

image-20221208220146206

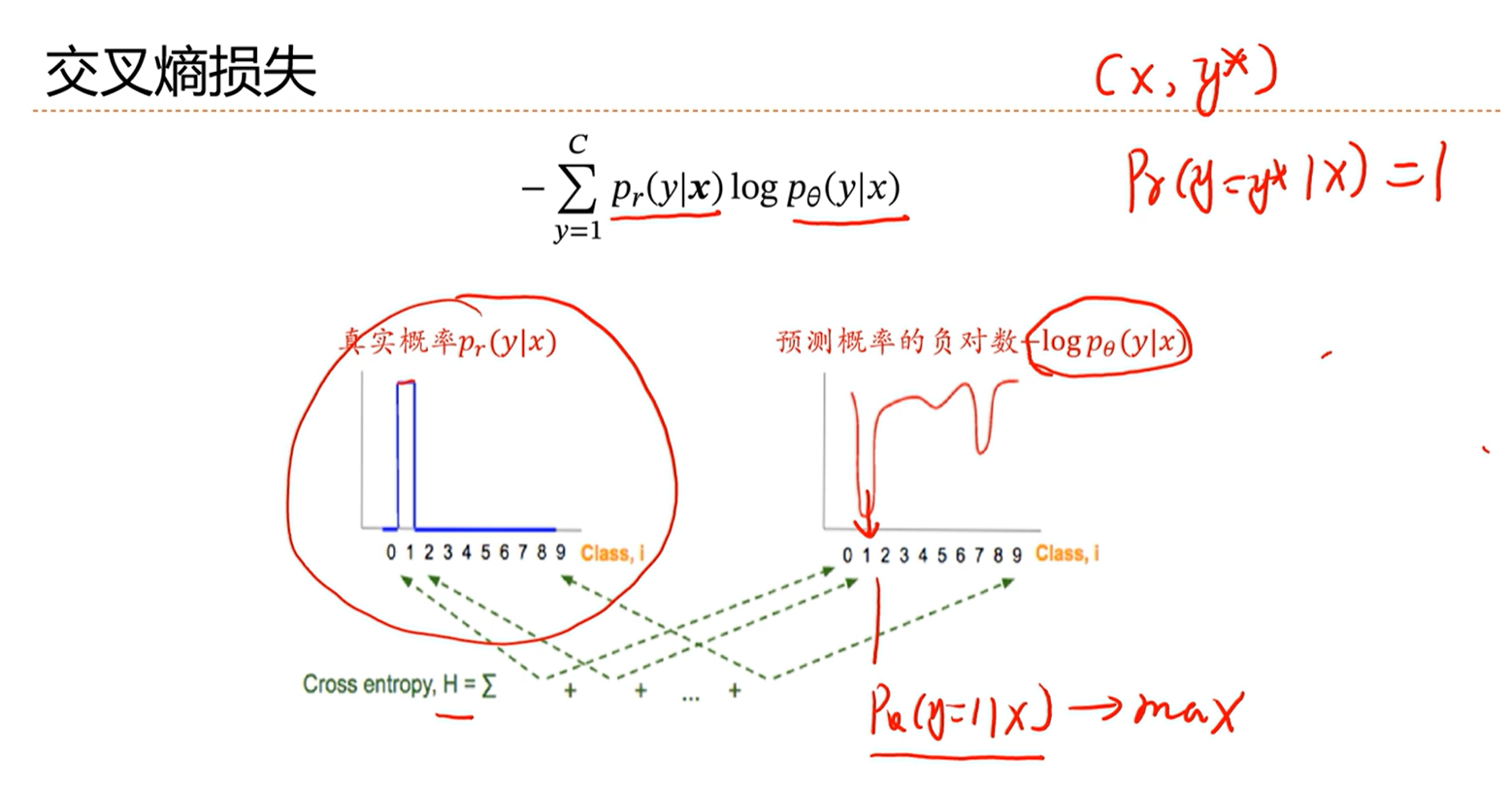
交叉熵可以用来衡量两个分布的差异。如果两个分布越近，那么蕴含的信息越少，交叉熵越小。

KL散度

image-20221208220427328

image-20221208221107423

3.4 - 具体的线性分类模型：Logistic回归

逻辑判断函数是不可导的，因此不能通过优化损失来学习。因此就需要一个可导的损失函数来优化。

因此需要将分类问题转换为概率的估计问题。通过交叉熵来建立损失函数。

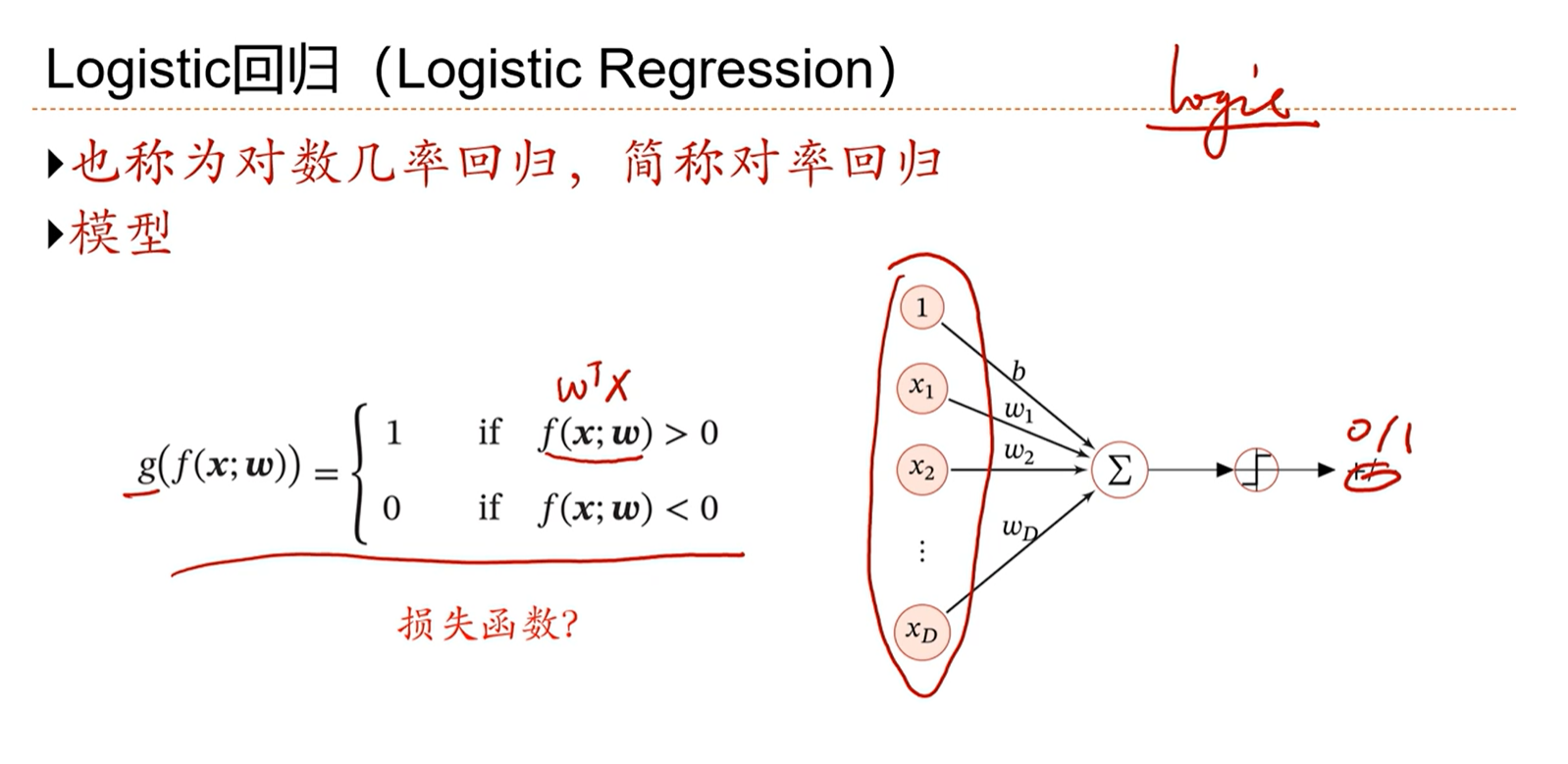
image-20221208222452651

image-20221208222919588

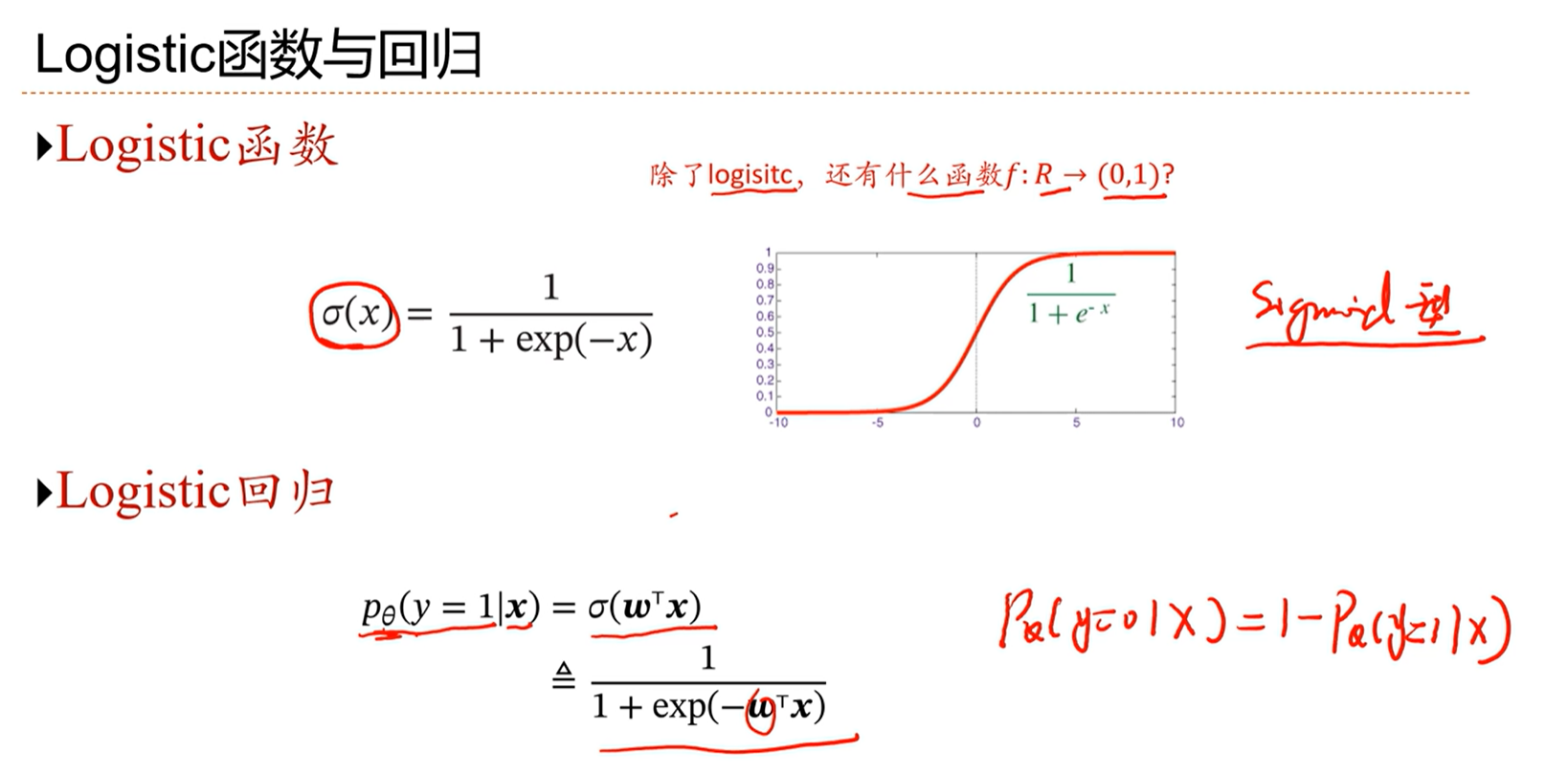
image-20221208223403392

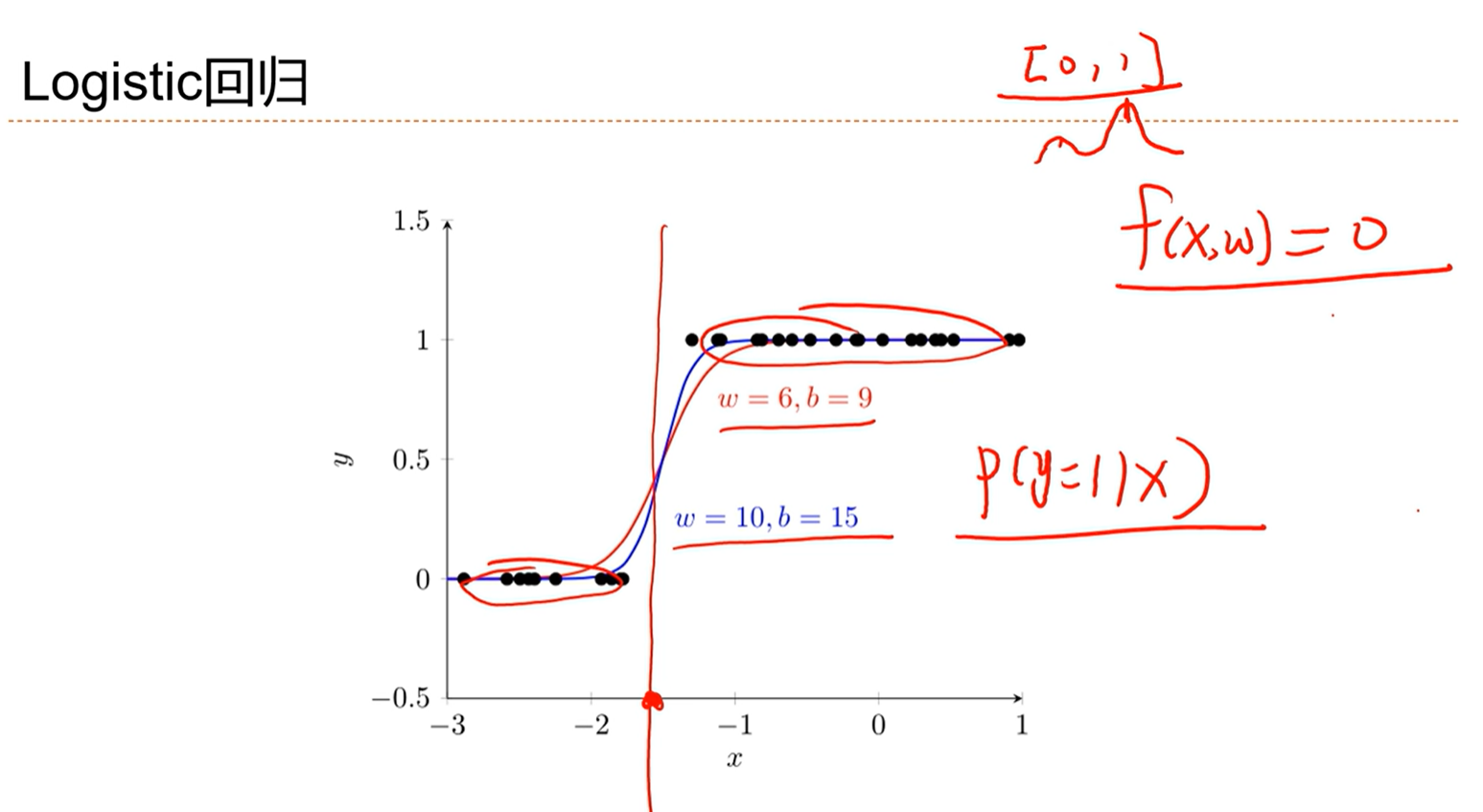
σ(x)通常被指代为logistic函数。

通过这种方式，将实数域的值映射到（0,1）之间，转化为0-1之间的概率分布问题。

image-20221208223833903

image-20221208224347080

image-20221208224619407

3.5 - Softmax回归

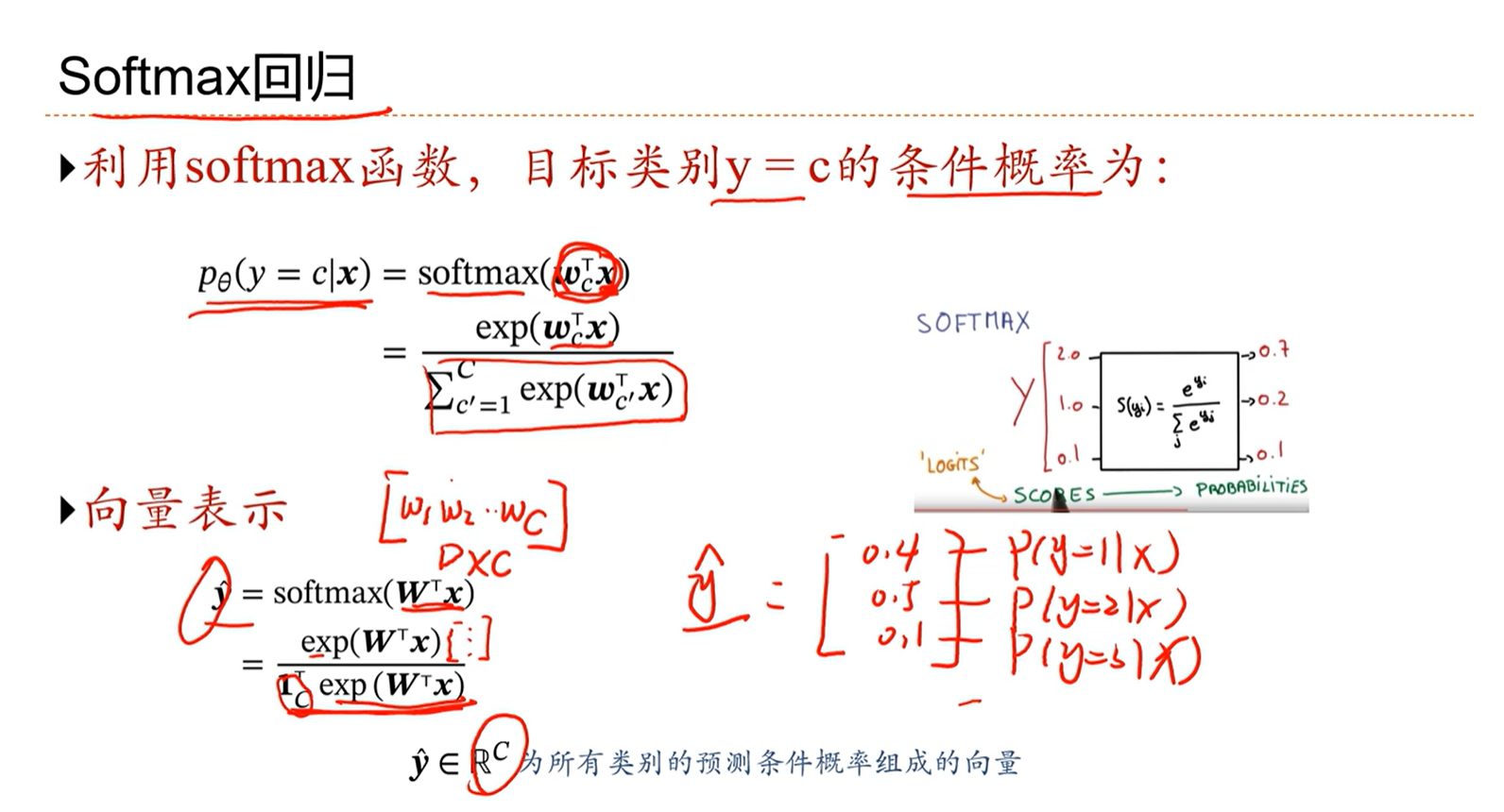
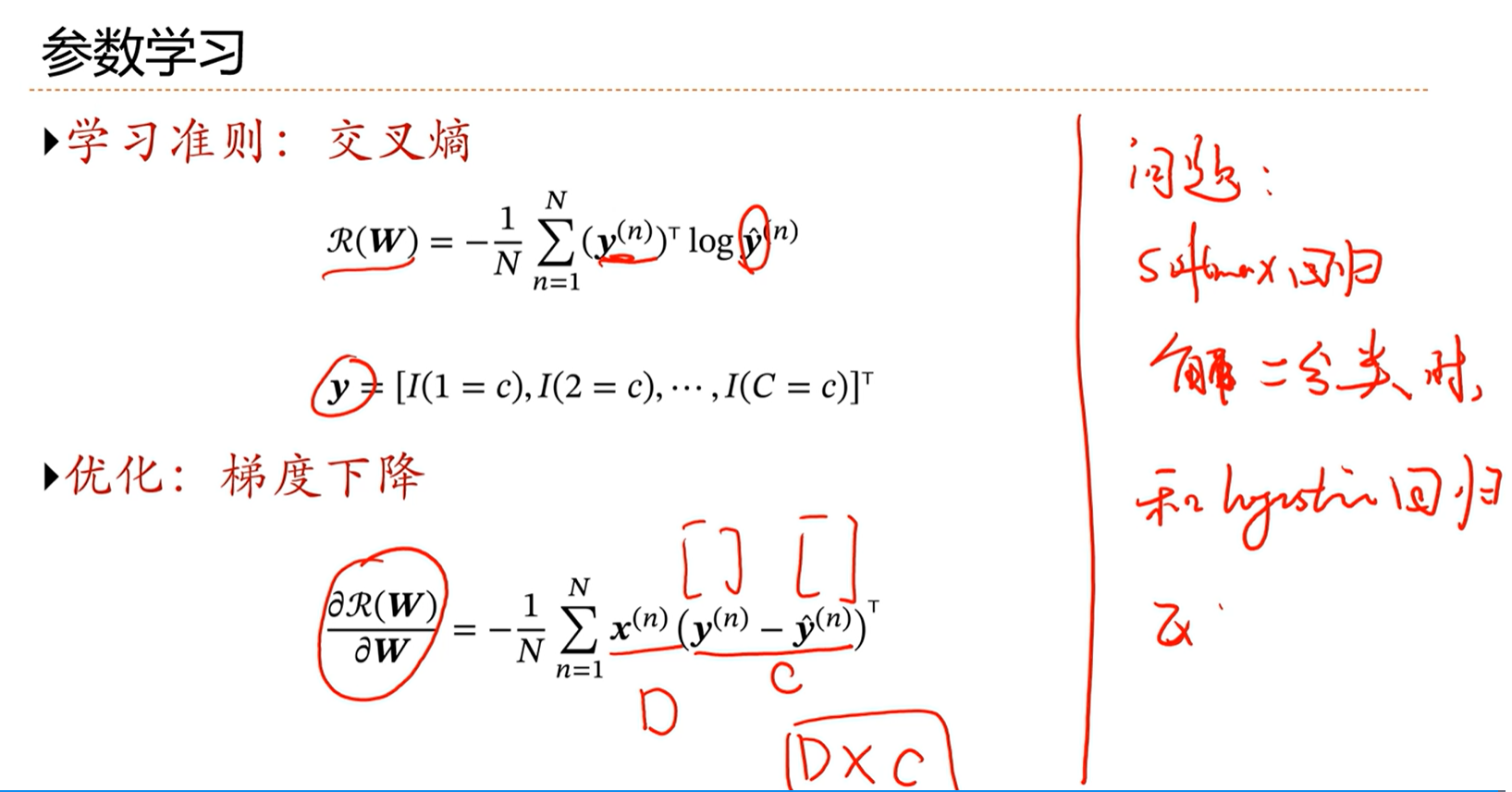
logistic回归是用于二分类问题的，其在多分类问题下的扩展形式是softmax回归。

image-20221208225612942

image-20221208225923034

softmax函数，将预测的内容转化为总和为1的概率。

image-20221208230459772

image-20221208230719167

image-20221208230914312

image-20221208231205625

3.6 - 感知器

感知器目前是一个简单的线性分类器

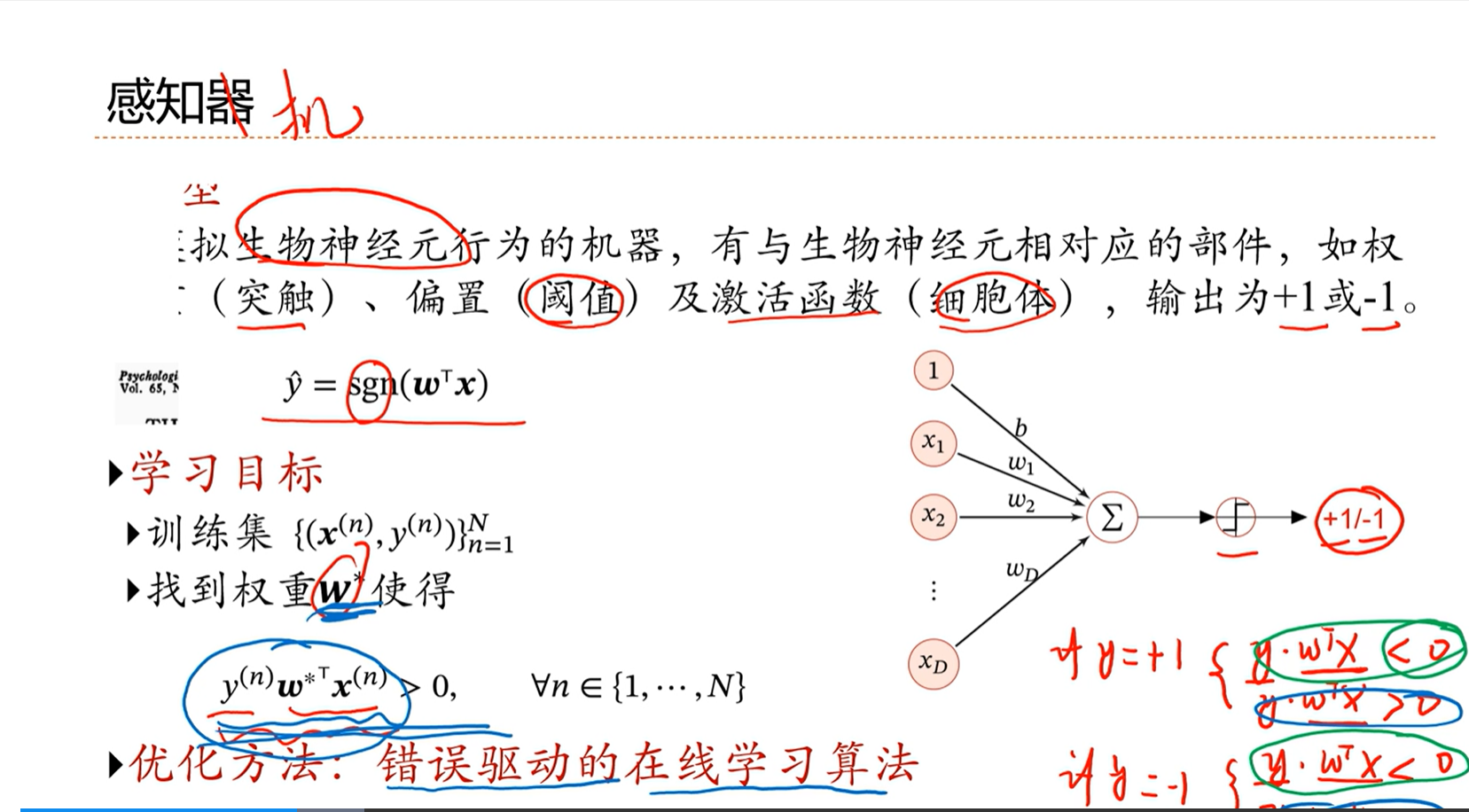
image-20221209135048024

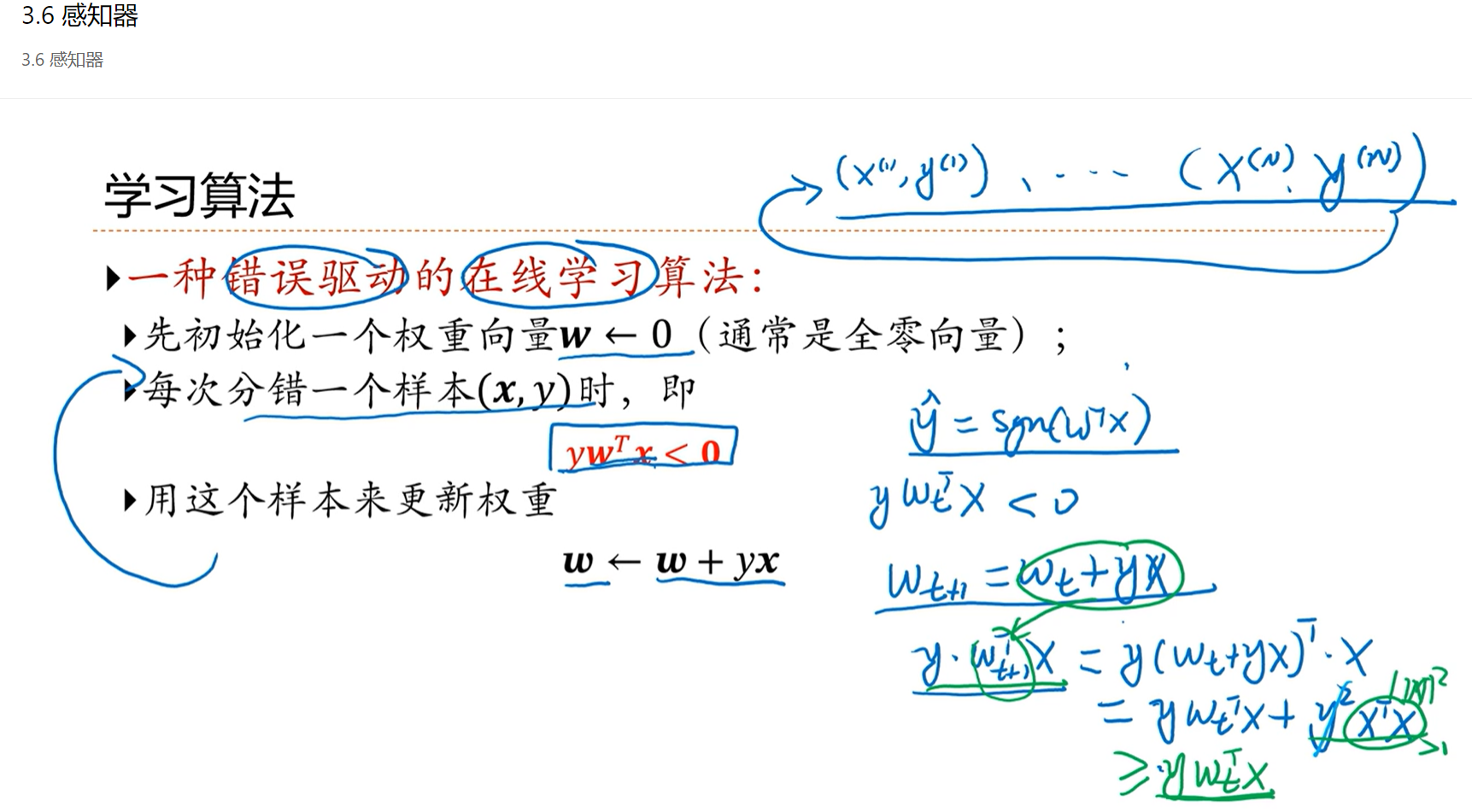
image-20221209135431524

image-20221209135755122

感知器这种学习方式类似于现有的随机梯度下降算法，即每次选择一组数据进行训练更新。

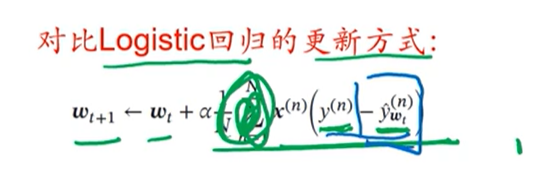
image-20221209140126702

对于logistic回归来说，参数w的更新，要看犯错的程度，如果输出和标签之前的差异越小，那么参数w的更新越小。

image-20221209140257280

而感知器是不参考犯错的程度的，只要犯错就按照特定的方式更新。

但是感知器在正确分类的时候是不更新的，这一点是比较好的。

感知器的更新过程

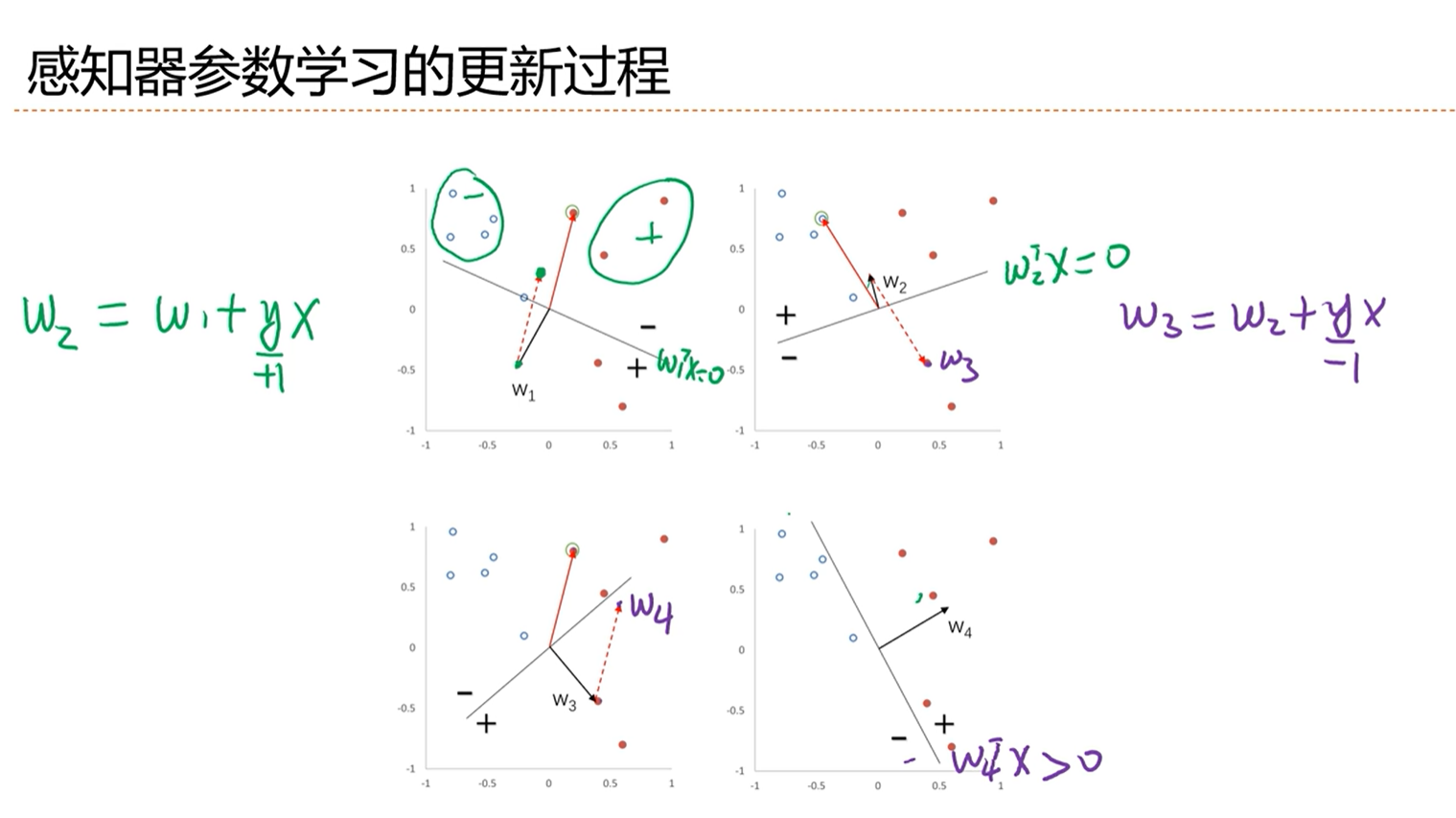
image-20221209140850180

感知器很好的性能：收敛性

如果数据集是线性可分的话，那么模型一定会在有限的更新次数内找到使得数据分开的权重

image-20221209141216585

image-20221209142003870

3.7 - 支持向量机

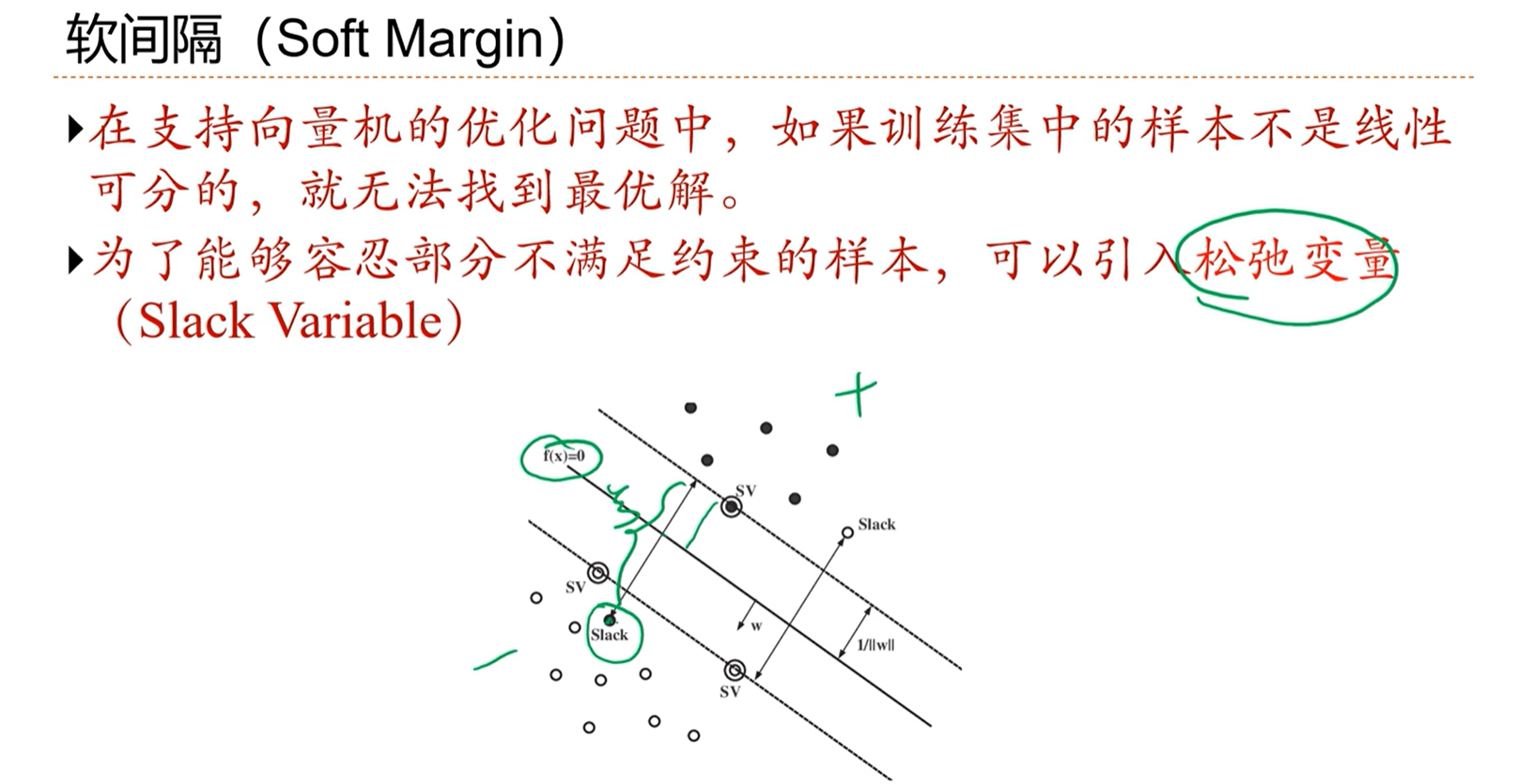
感知器存在的问题：分界面有可能找到多个，能不能找到一个最好的分界面？

理想的分界面是距离所有的数据有比较远，这样直观上感觉健壮性会更好。

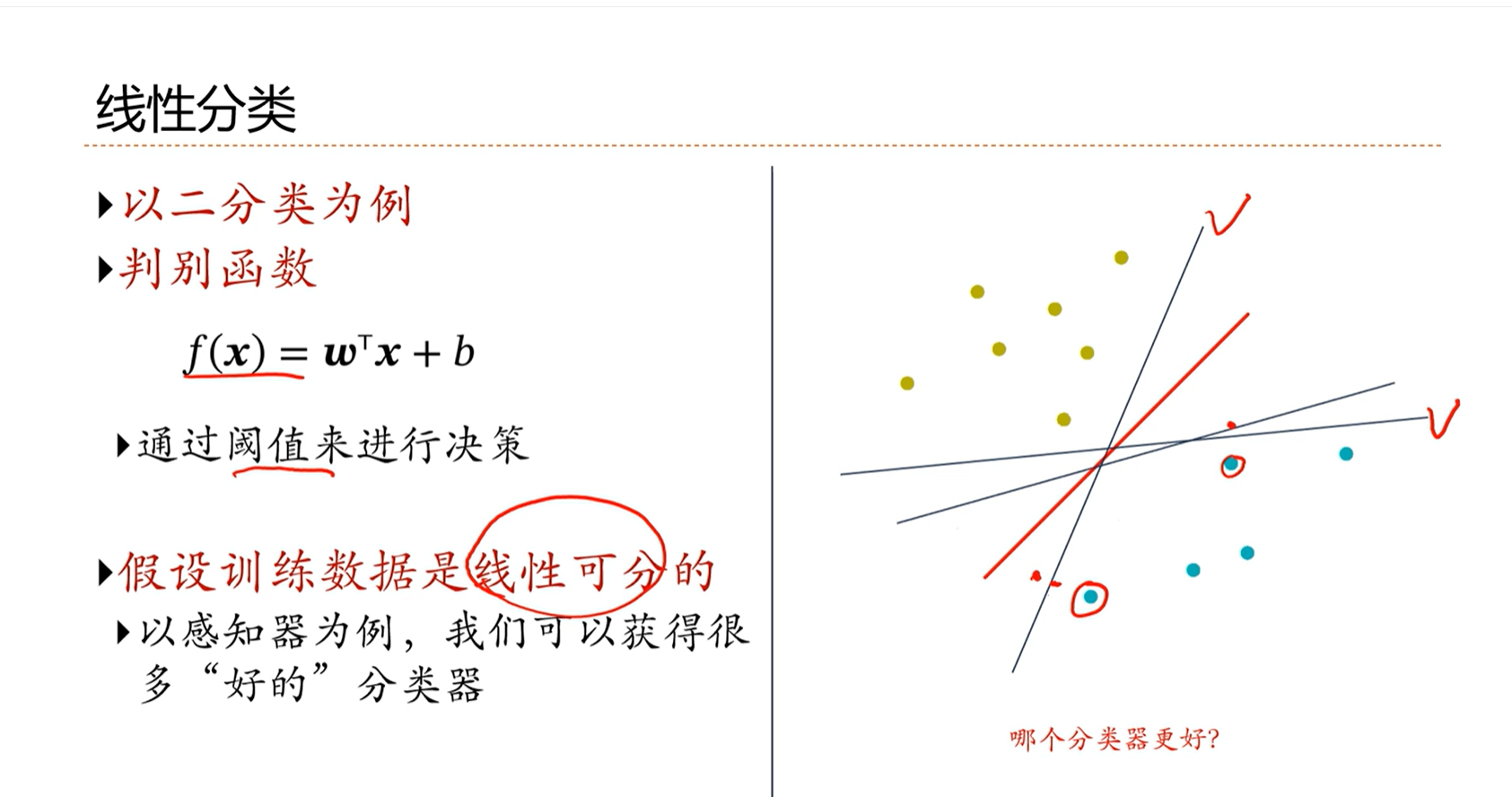
image-20221209142417975

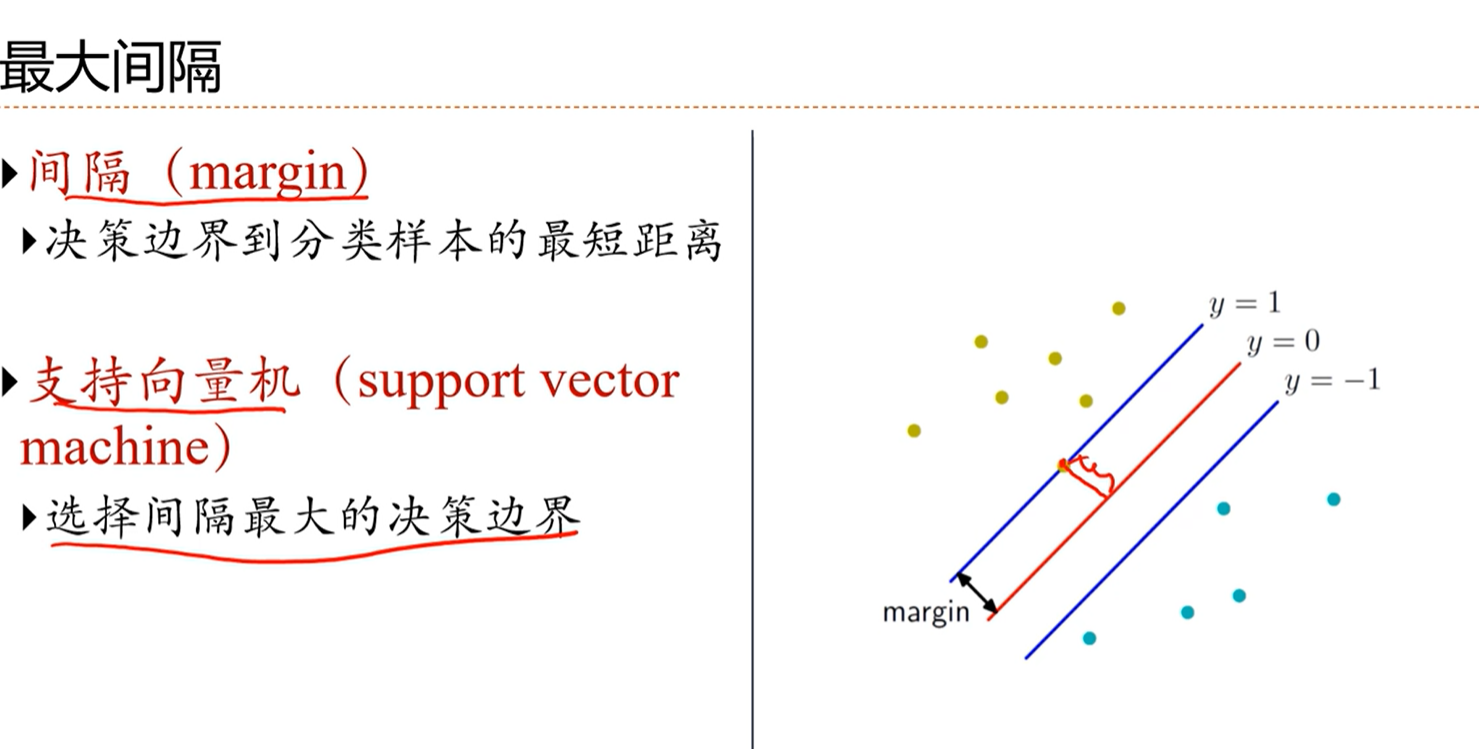
image-20221209142511906

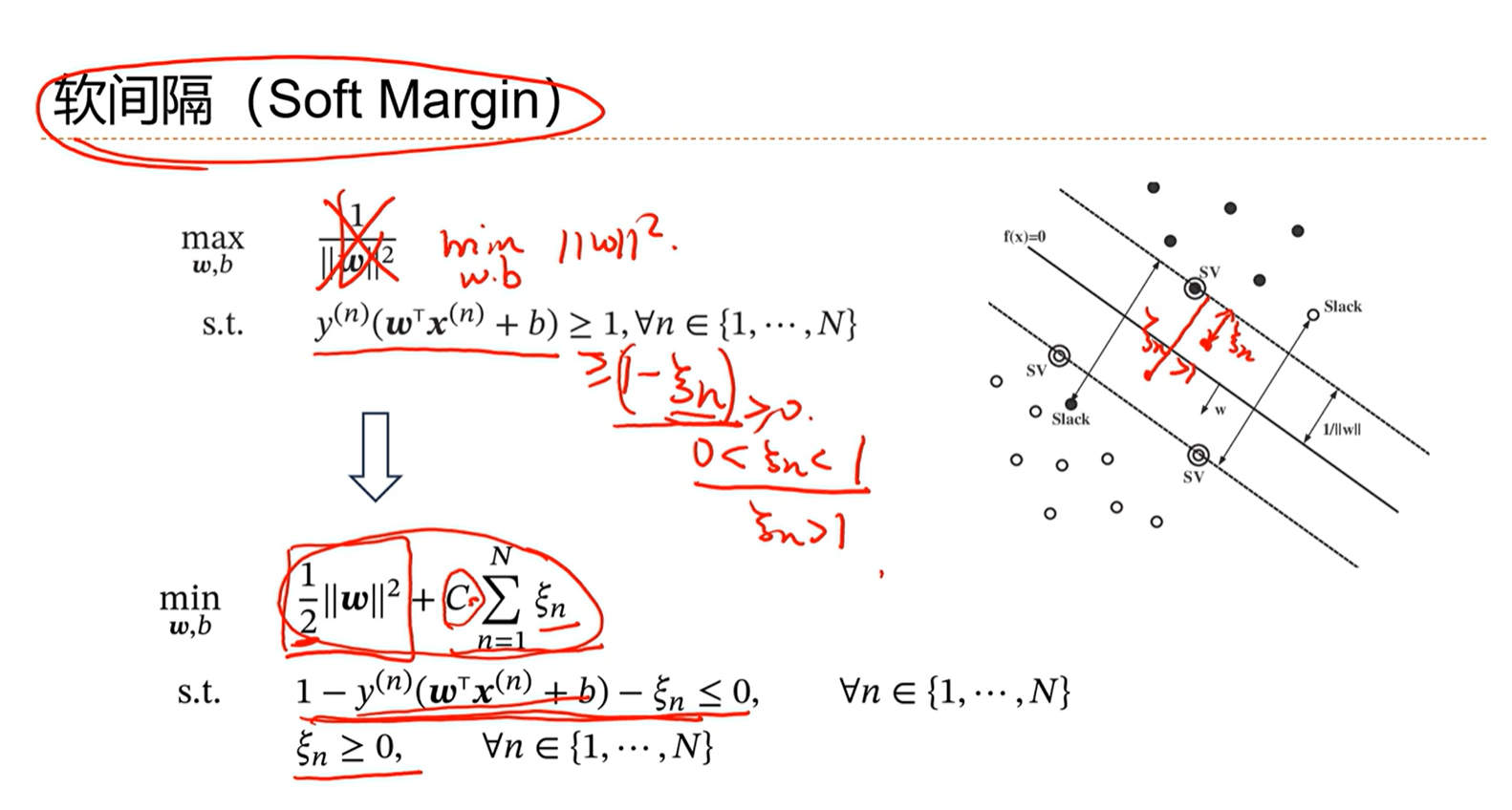
支持向量机的优化标准就是选择间隔最大的分界线。

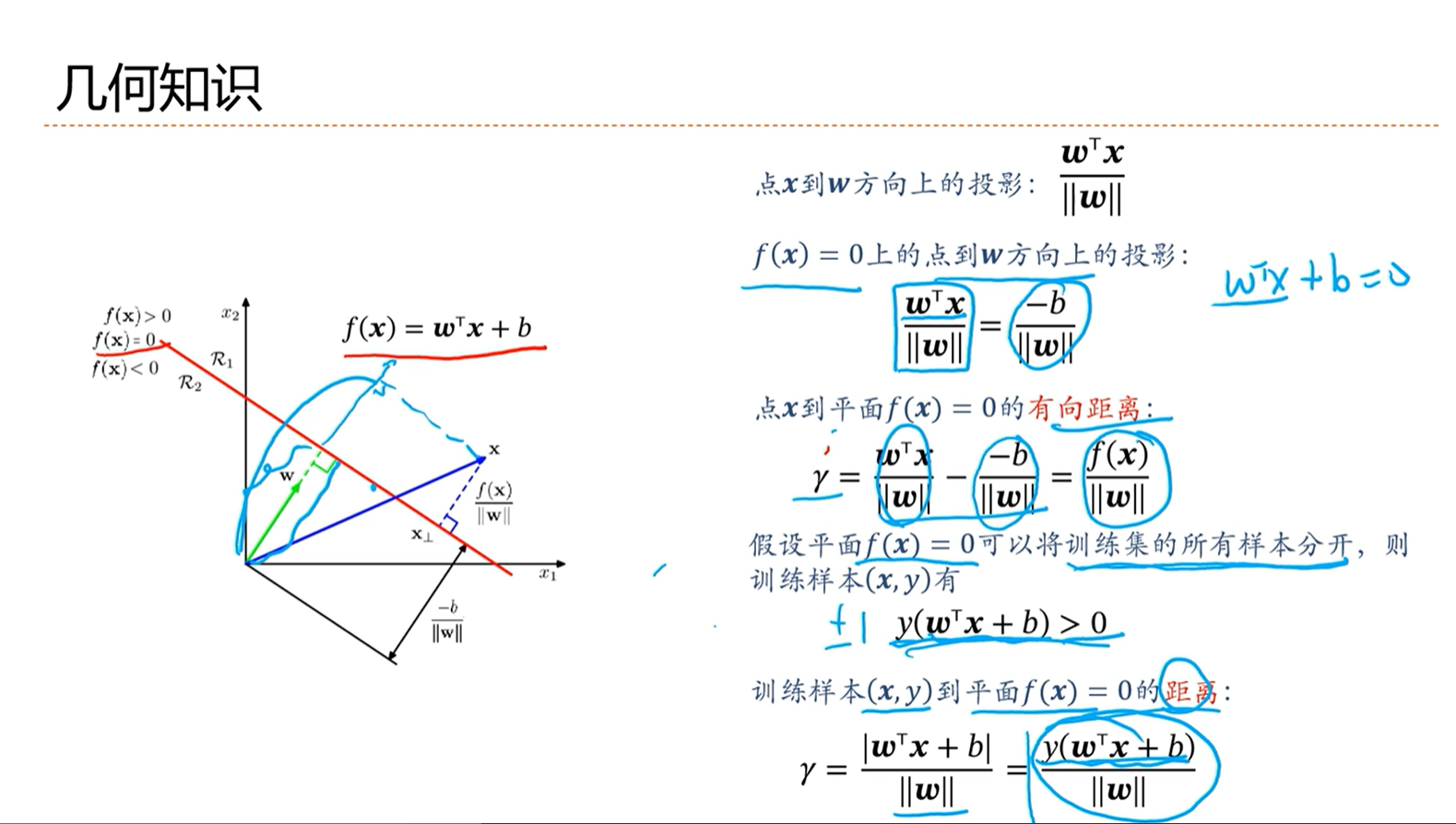
image-20221209143003355

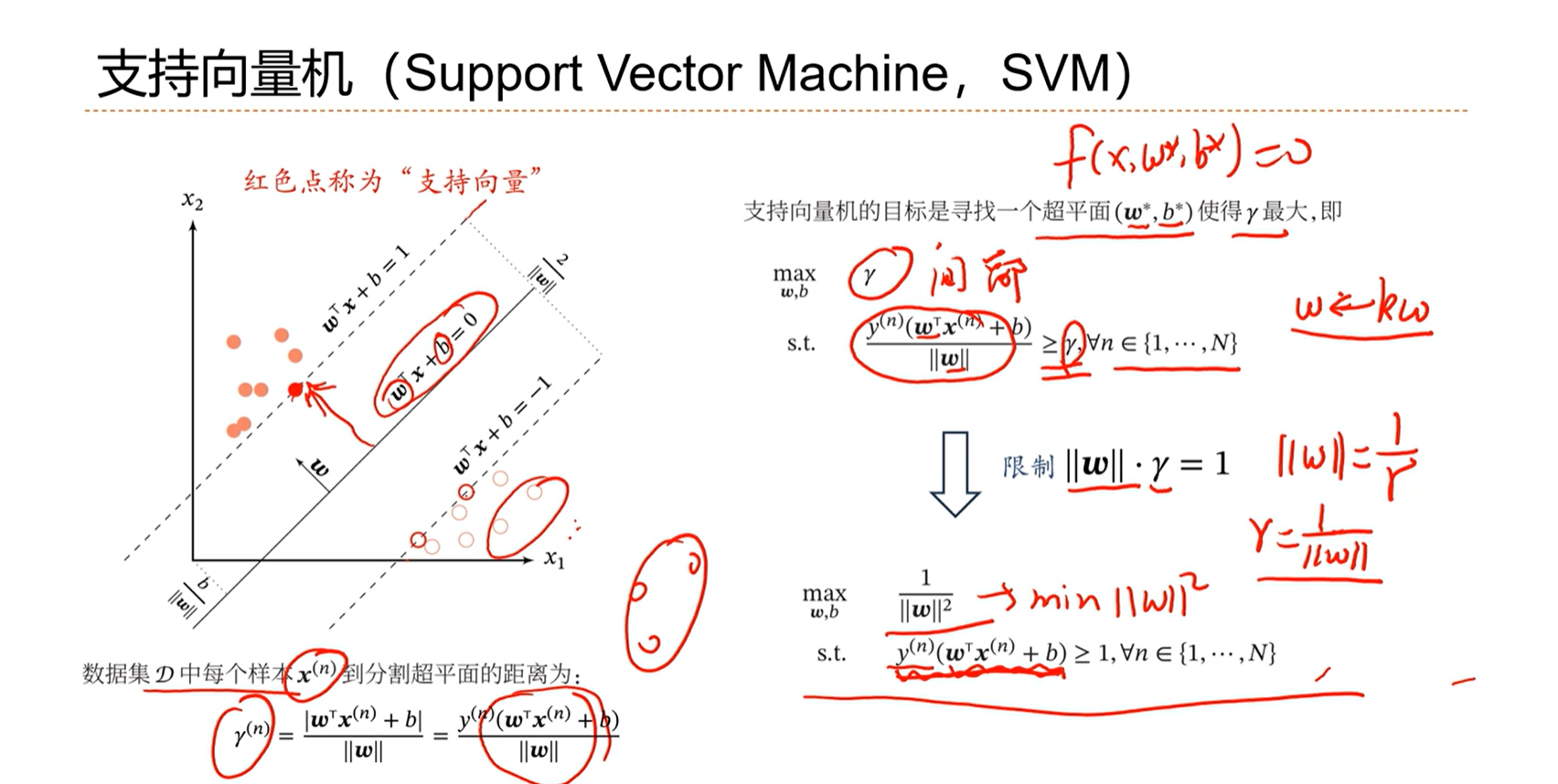
image-20221209143355250

image-20221209143527567

image-20221209151217297

image-20221209151930652

image-20221209152107398

3.8 - 线性分类模型小结

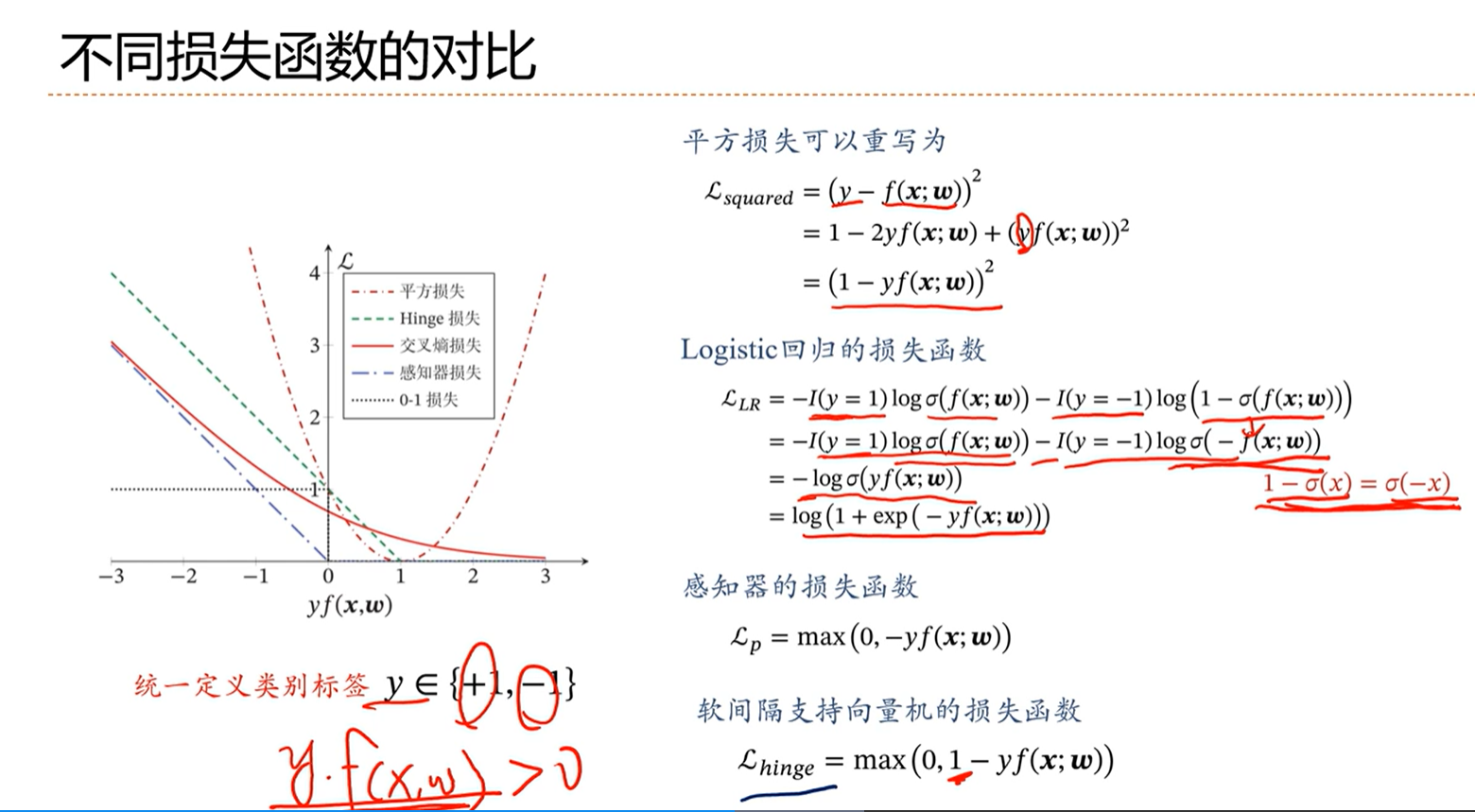
image-20221209154000340

yf(x;w)为正的话，表示分类正确，为负数表示分类错误，且该数越大则表示分类越正确。

==平方损失分析：==

当yf(x;w)大于1的时候，随着增大应该，损失应该减小，但是在图中看出损失却随着yf(x;w)的增加而增大，因此平方损失是不适合做分类任务的。

==logistic回归的损失函数：交叉熵损失函数==

在图中可以看出，随着yf(x;w）的增加，损失是下降的。这样是合理的。

虽然是合理的，但是在分类正确的情况下可以看出交叉熵损失仍然是有惩罚的，因此虽然合理，但是对于分类任务来讲，分类正确仍然惩罚是没有必要的。这个损失函数依然有改进的空间。

==感知器的损失函数：==

感知器的损失可以看出是标准的为分类而设计的，如果小于0则有损失，如果大于0分类正确则没有损失。

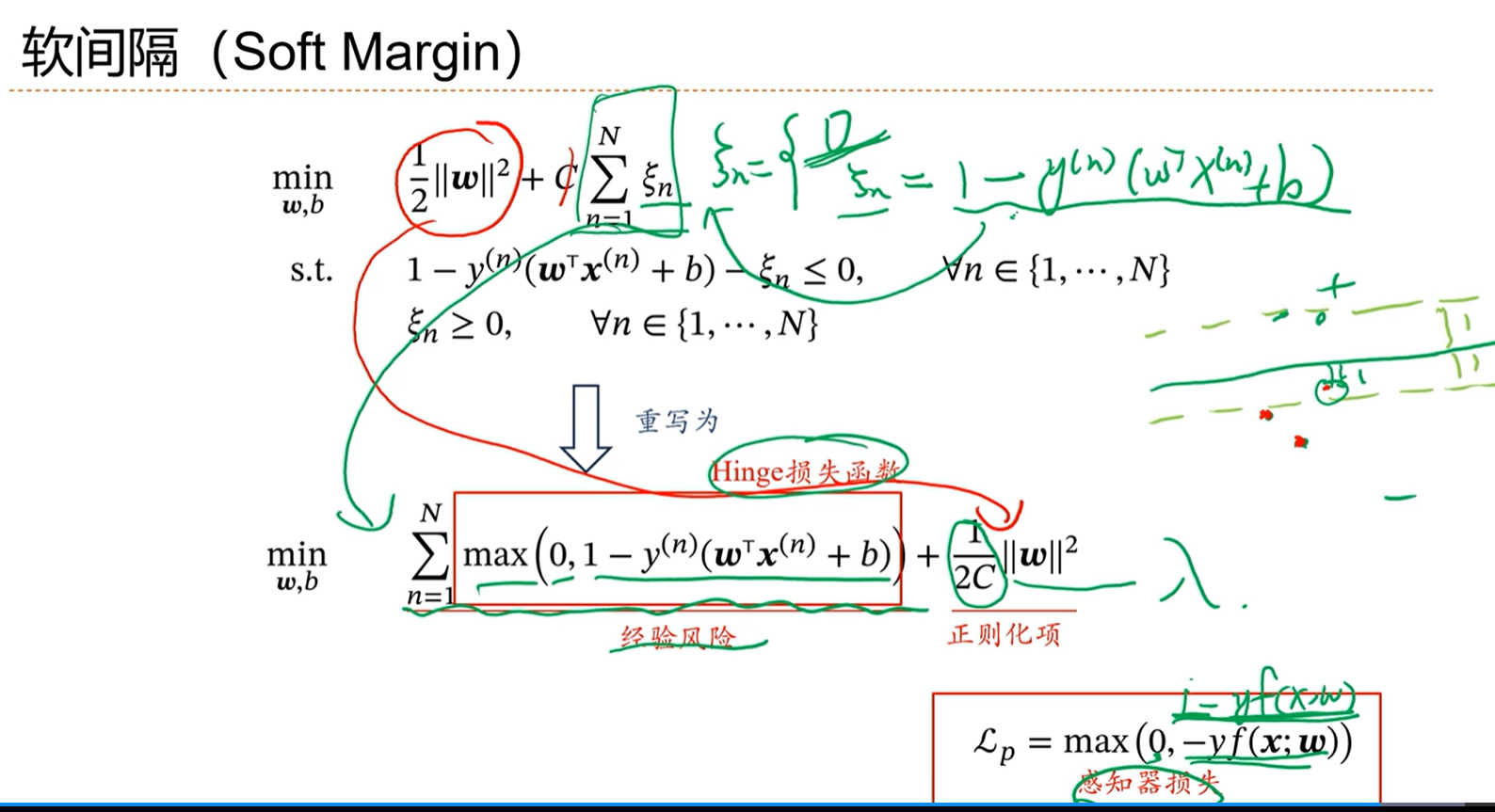
==软间隔的支持向量机的损失函数：==

在距离边界比较近的地方，依然是有惩罚的。

软间隔的SVM的loss在直觉上会带来更好的效果。

线性分类模型小结

image-20221209154049507

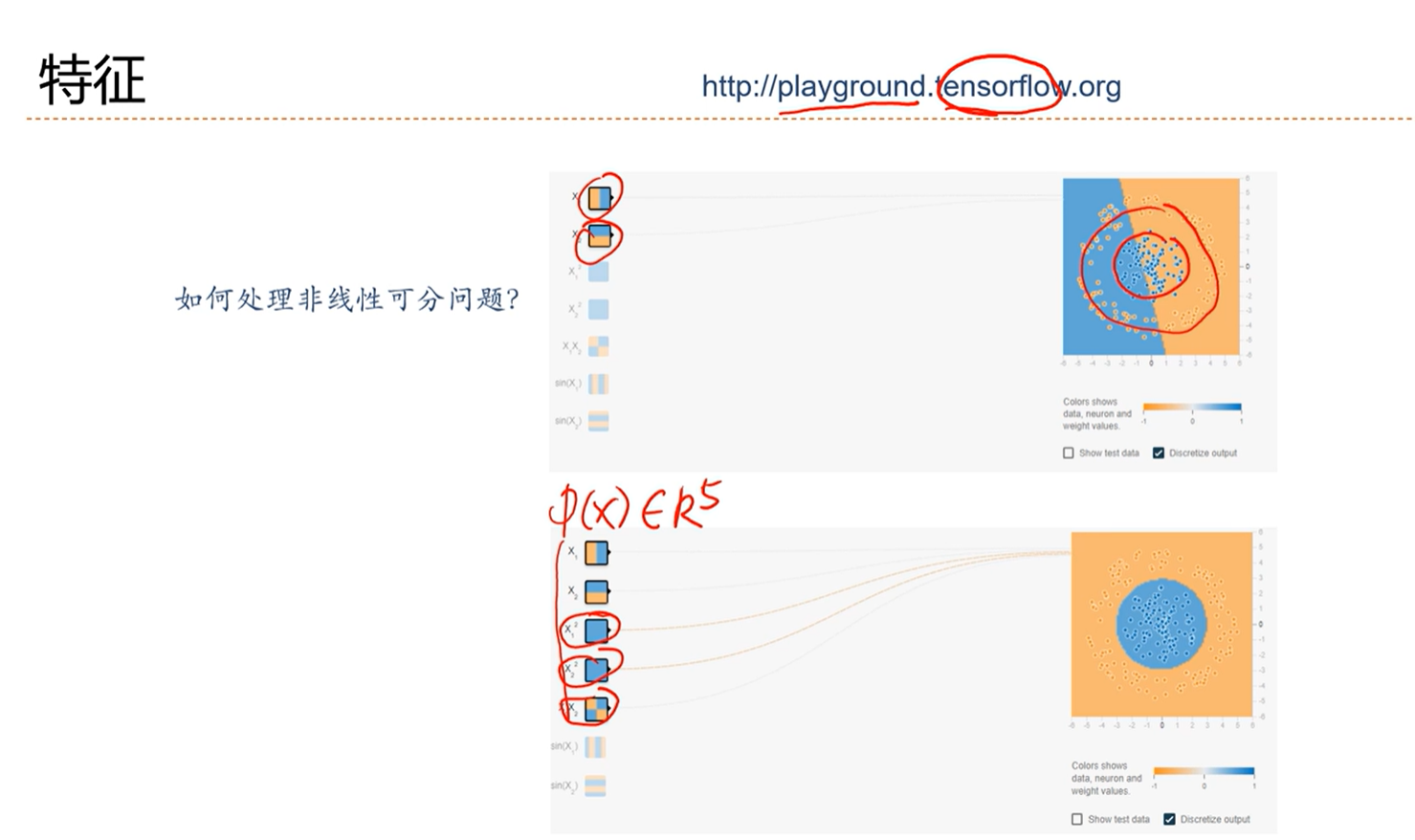
线性分类器无法解决非线性问题

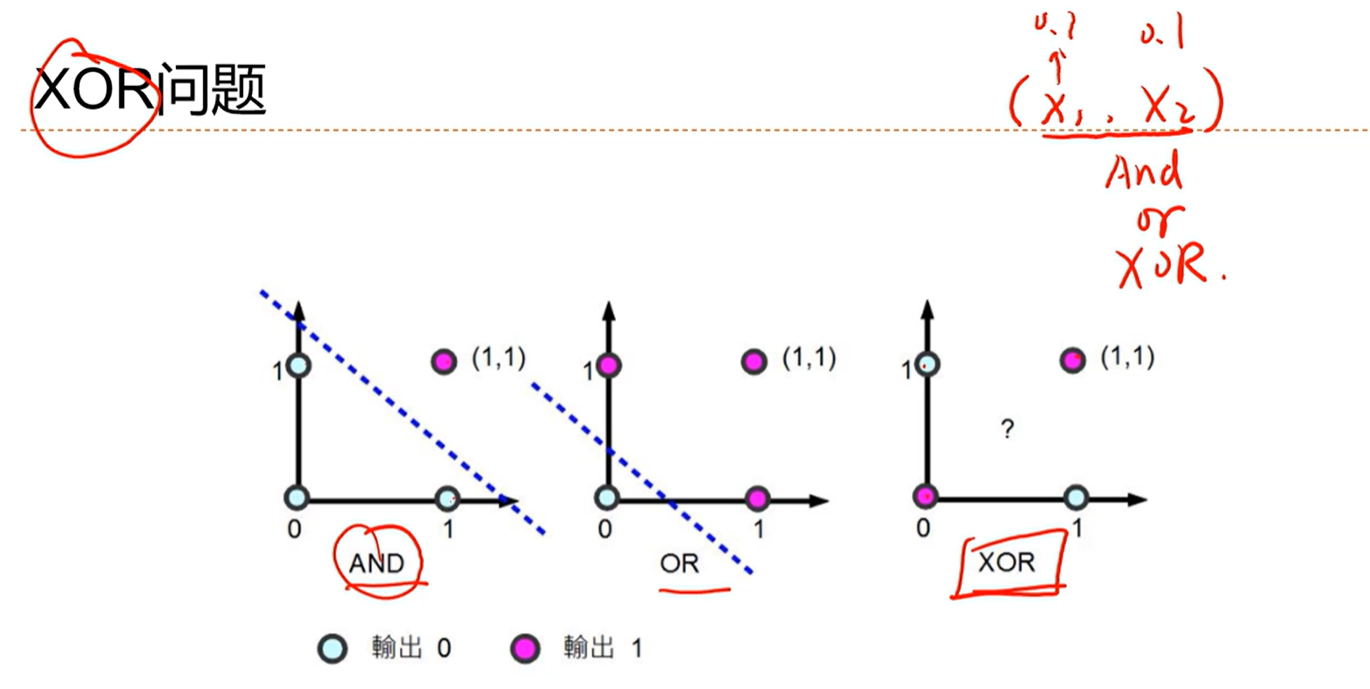
image-20221209154332443

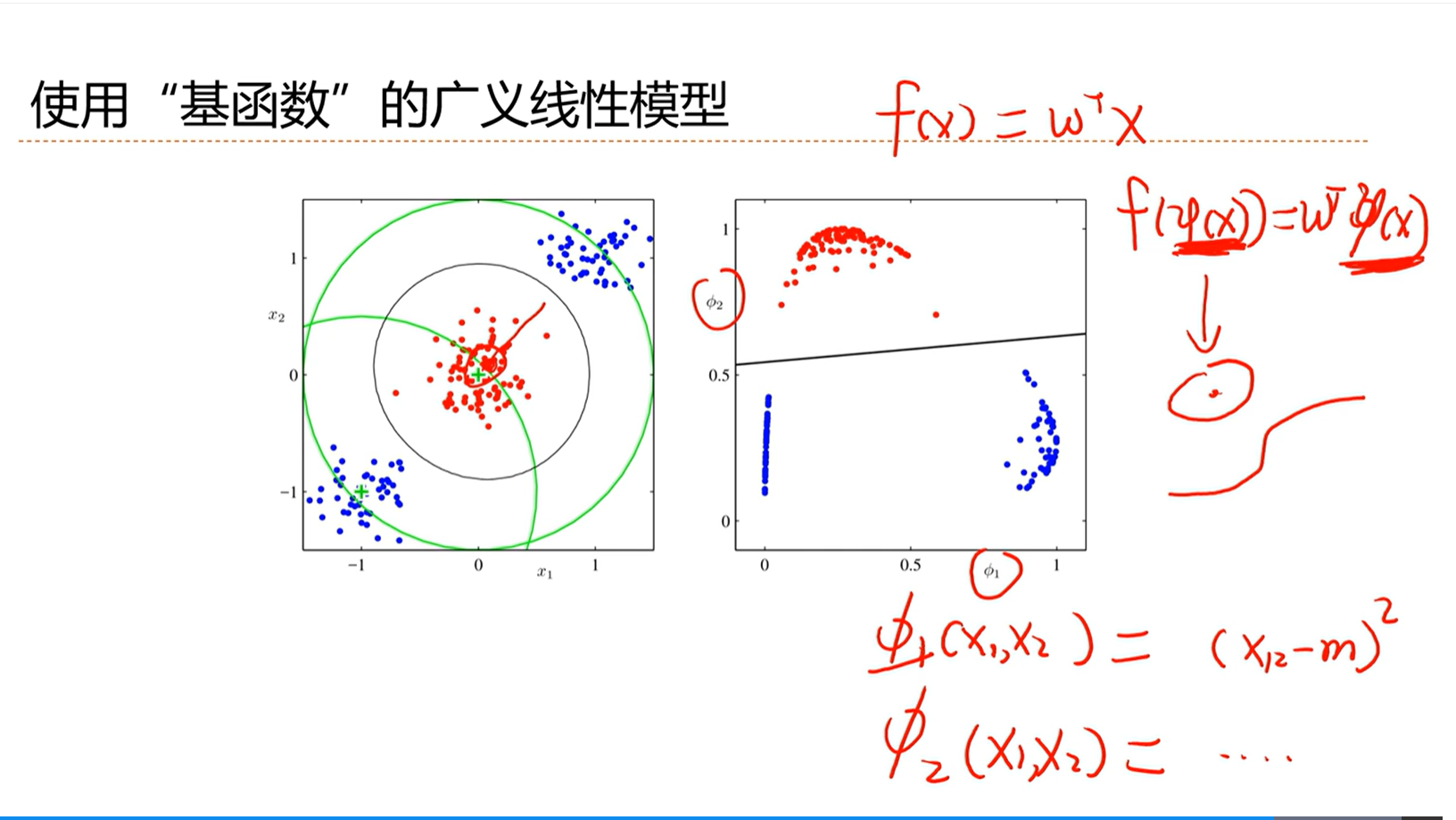
使用“基函数”的广义线性模型解决非线性问题的分类问题

使用基函数，将分布映射到另一个可分的空间就可以进行分类了

image-20221209154631205

image-20221209154734740