006 - 文章阅读笔记：向量的内积和外积

原文链接：

矩阵外积与内积

一个行向量乘以一个列向量称作向量的内积，又叫作点积，结果是一个数；

一个列向量乘以一个行向量称作向量的外积，外积是一种特殊的克罗内克积，结果是一个矩阵，

向量的点乘,也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。

点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影，有公式：

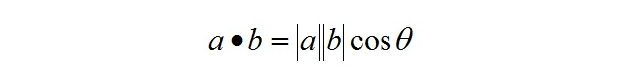
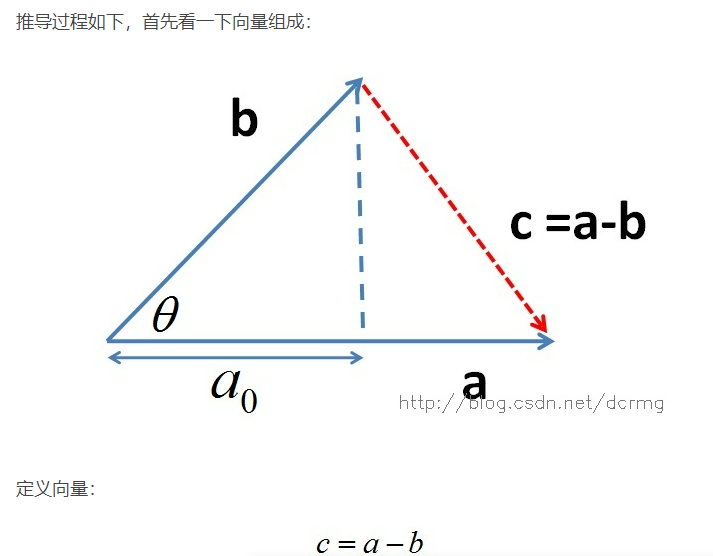
叉乘公式

两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。

叉乘几何意义

在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。

在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。如下图所示：

在二维空间中，叉乘还有另外一个几何意义就是：aXb等于由向量a和向量b构成的平行四边形的面积。