7 - 网络优化与正则化 - 视频
本文最后更新于:3 个月前
[√] 7.1 - 批大小调整实验
[√] 网络优化与正则化

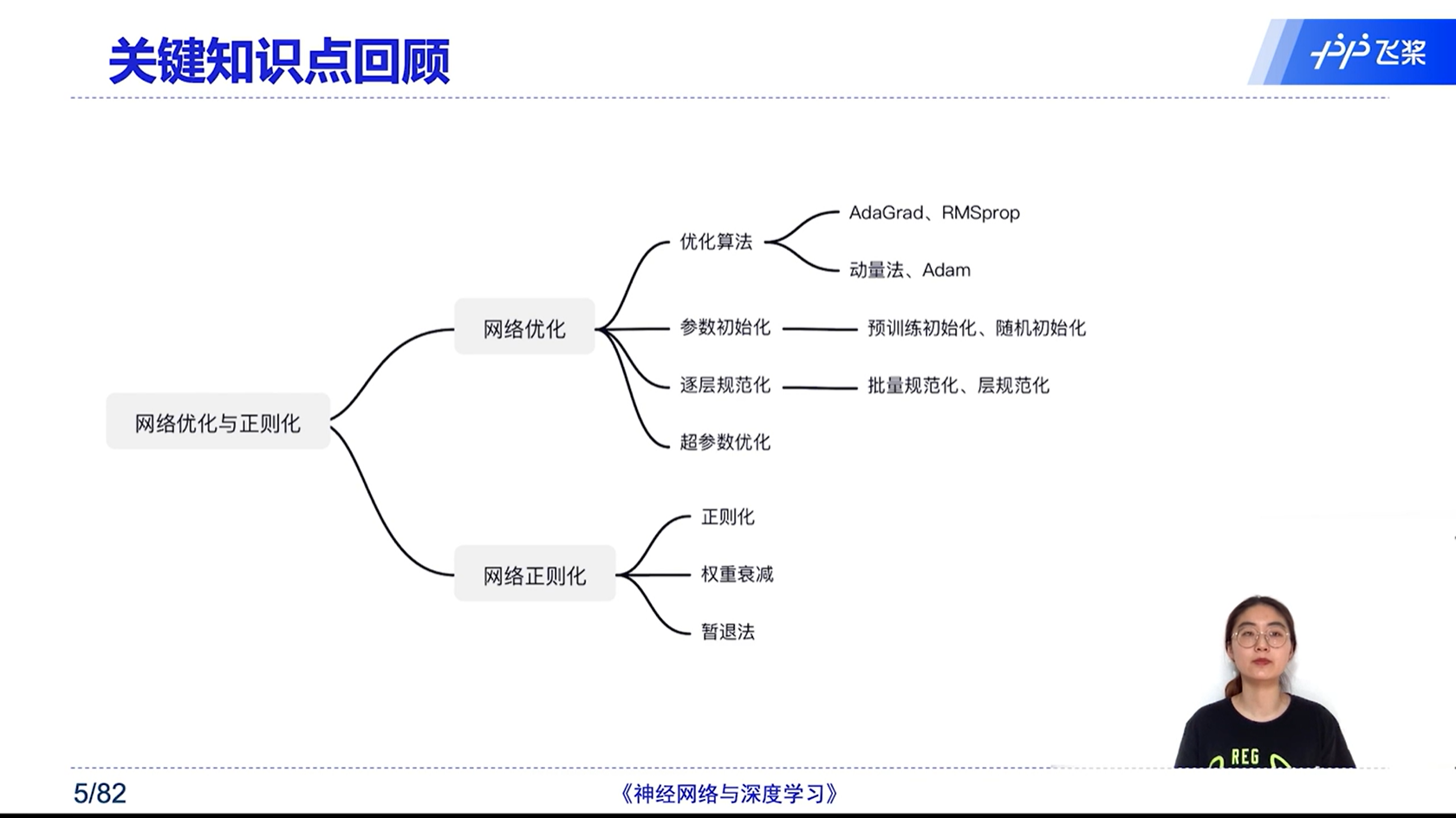

[√] 小批量随机梯度下降

[√] 批大小的调整实验

alec:
- 学习率和批大小成正比,因为批大小大,那么梯度的方差就小,引入的随机梯度的噪声也小,因此学习率可以相应的调大
alec:
- 通过该图能够看出,总体来说,批大小比较小的组,最终的损失最小。因为批大小比较小的组,每组的样本数量少,但是每一个epoch中能够迭代的iteration多,更新更多次,所以最终的损失更小。
[√] 实际训练中的批大小选择

alec:
- 实际中如何设置批大小呢?
- 虽然小的K能够达到更好的收敛效果,但是总的来看,大K的时候,既能够充分利用GPU的计算能力,提高计算效率;同时因为批大小大的时候,泛化能力更好。所以在实际中,尽量选择大的批次
- 当训练集非常大的时候,就不需要考虑泛化性问题了
- 目前比较sota的方法,倾向于使用256的批大小
- 下面的三个网络中,前两个用的是transformer,所以用的优化器是AdamW,目前这个优化器还没有比较固定的初始值
- 在训练的时候,可以先看看目前类似任务他们的网络初始值怎么设定的
- 迭代 = iteration、回合 = epoch
[√] 7.2 - 学习率衰减与学习率预热
[√] 不同优化算法的比较分析

[√] 学习率衰减
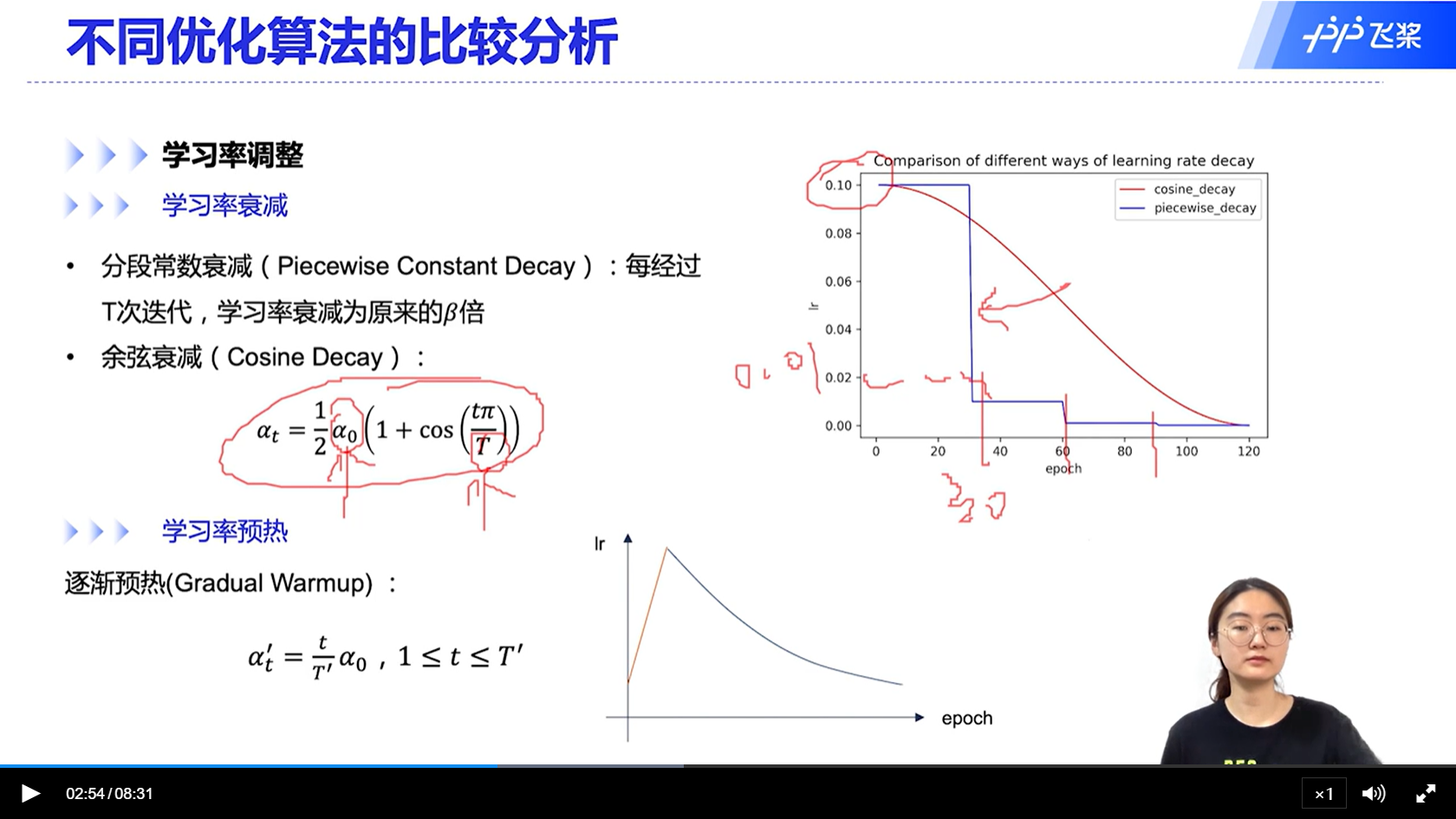
[√] 实际训练中的学习率调整

[√] 7.3 - 不同优化器的比较分析
[√] 优化算法的实验设定

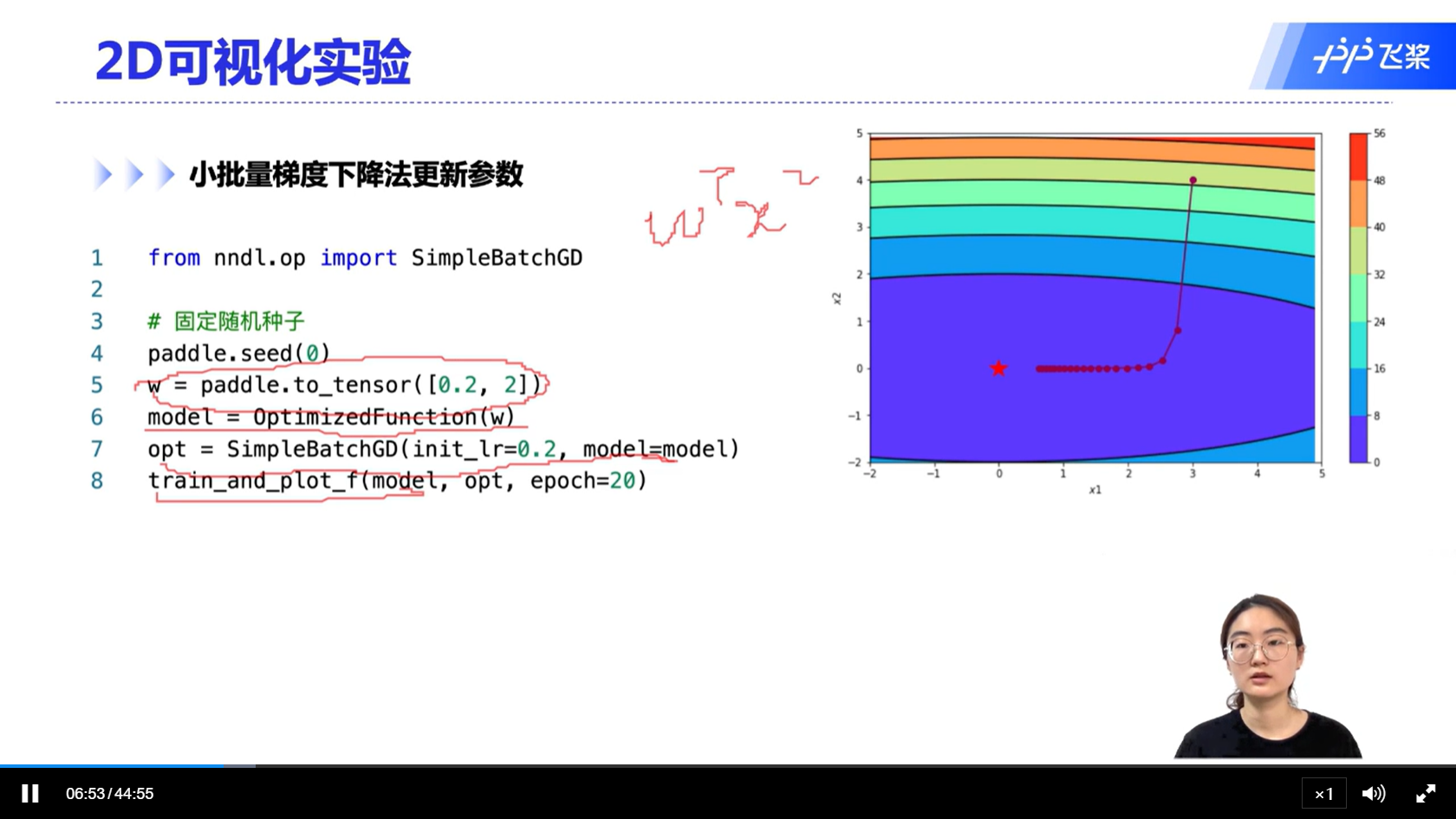
[√] 2D可视化实验



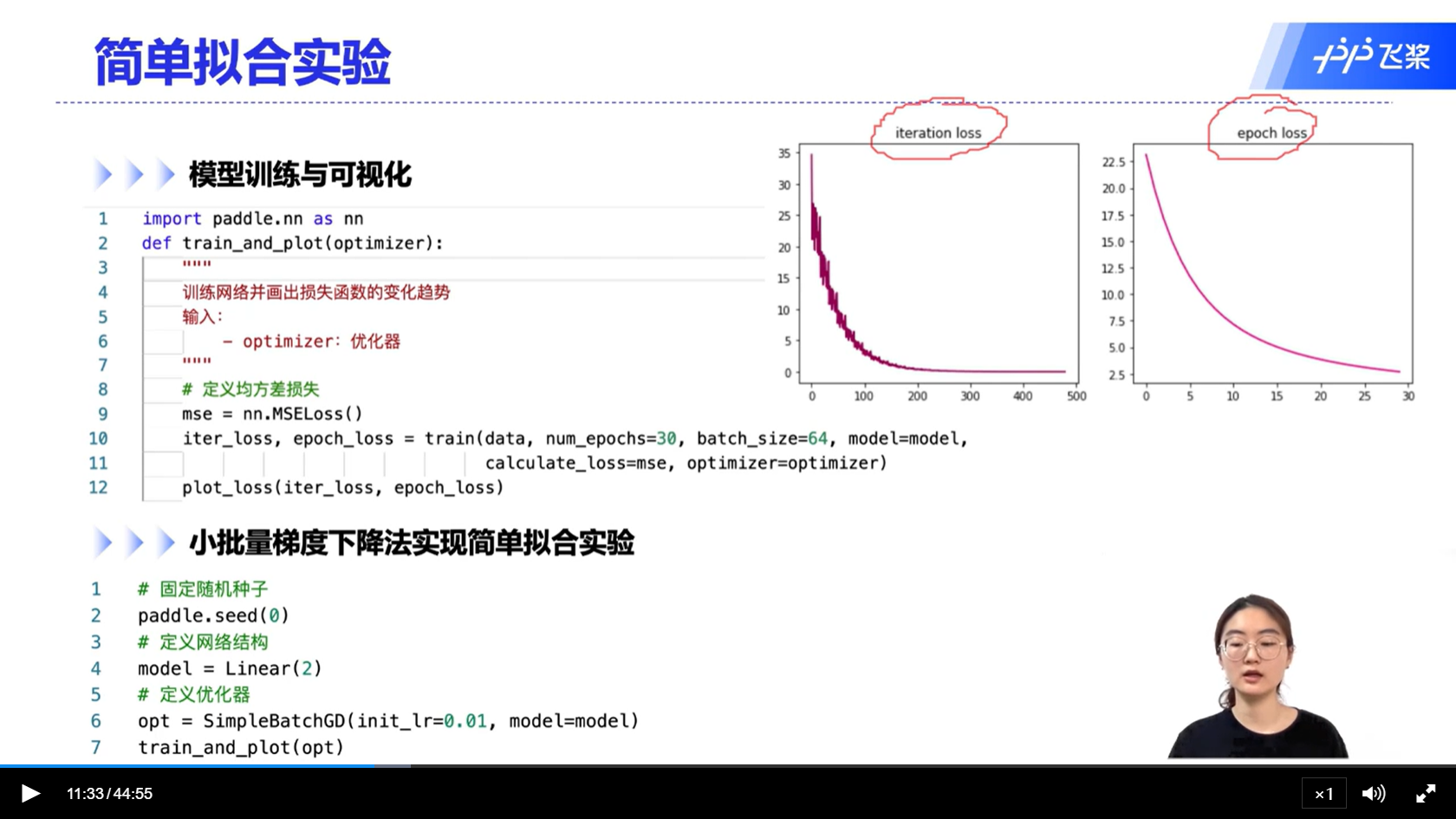
[√] 简单拟合实验
模拟优化器在真实的场景下的使用


[√] AdaGrad算法
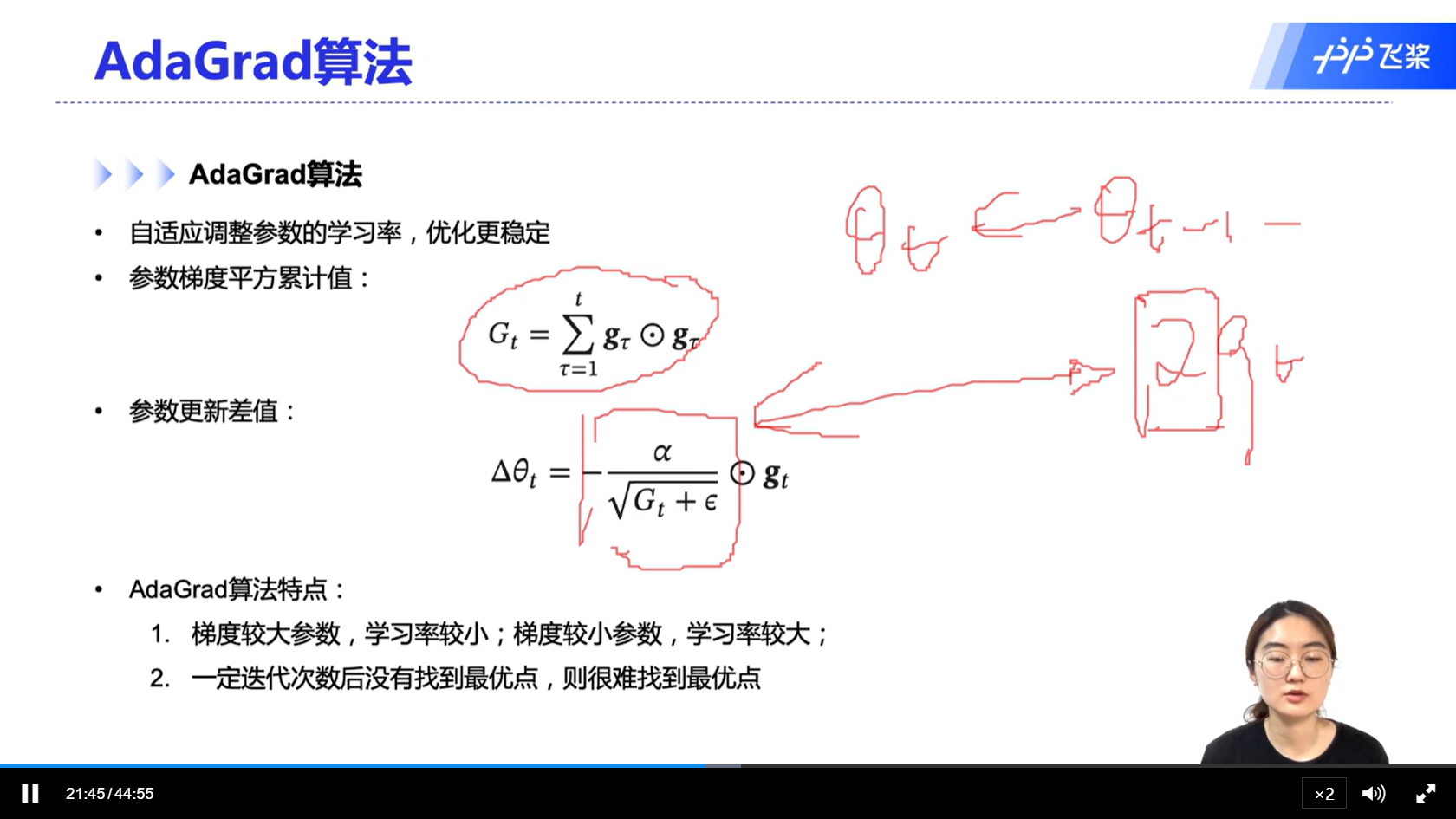

[√] RMSprop算法

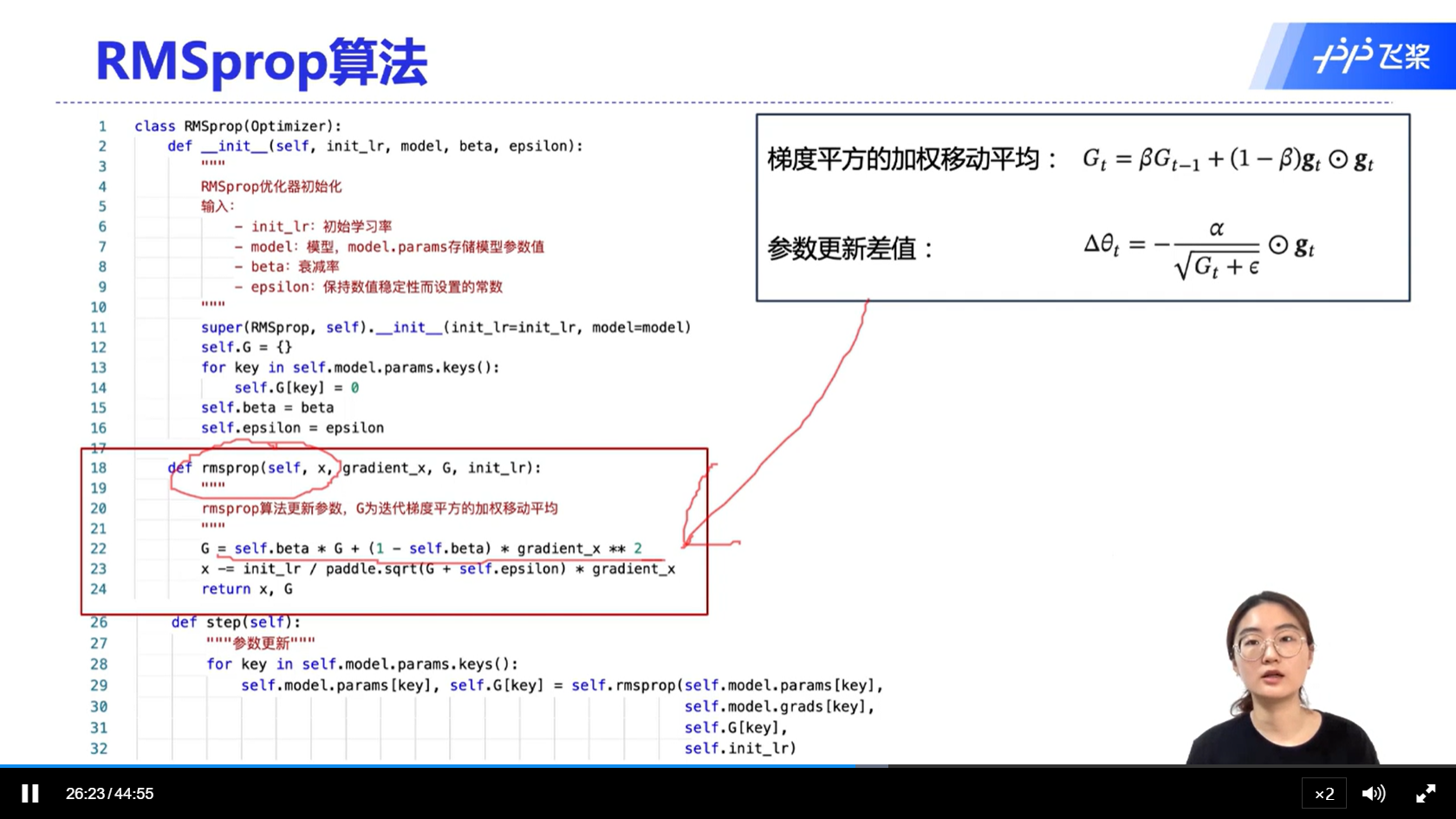
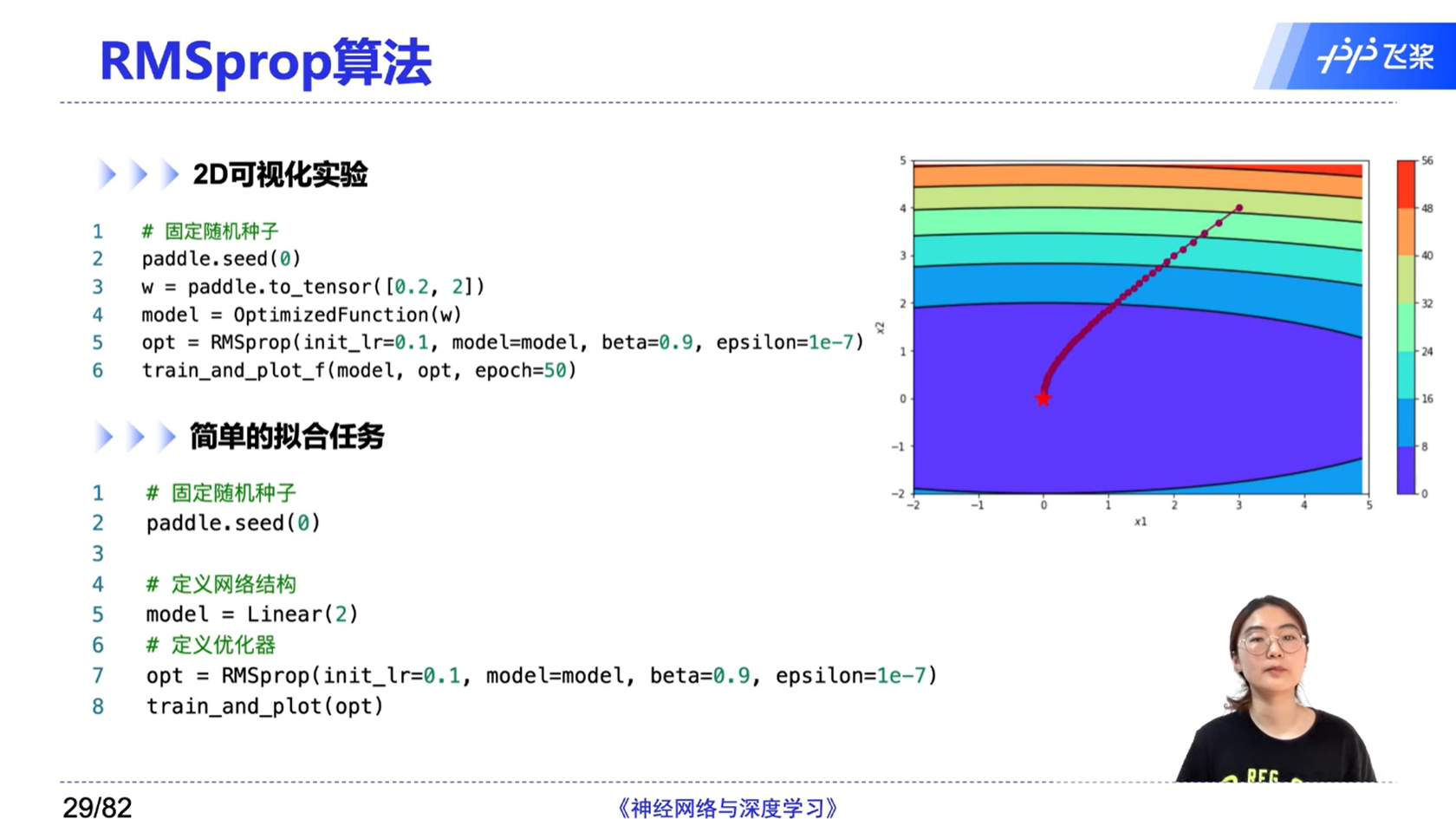

[√] 动量法
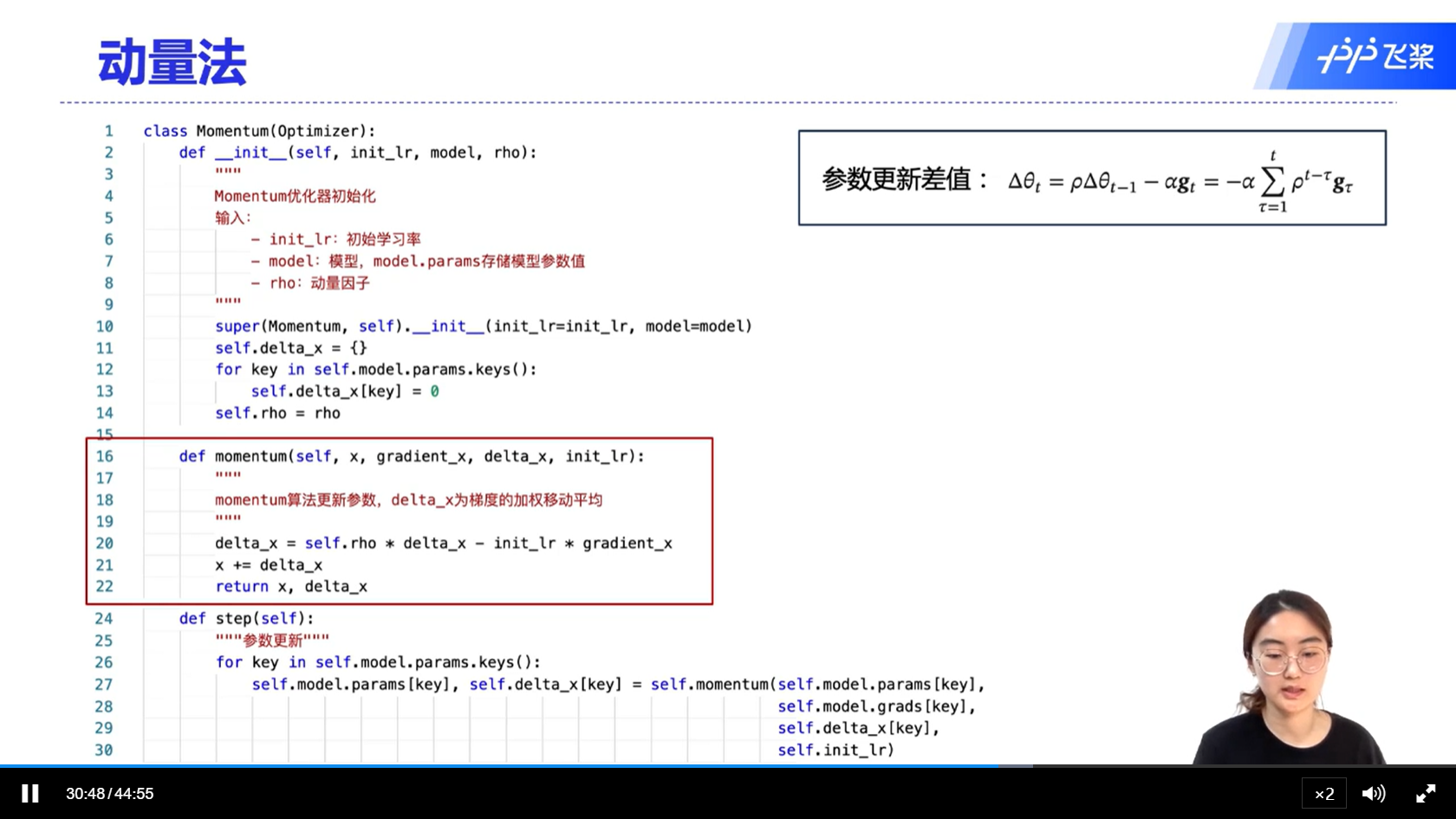
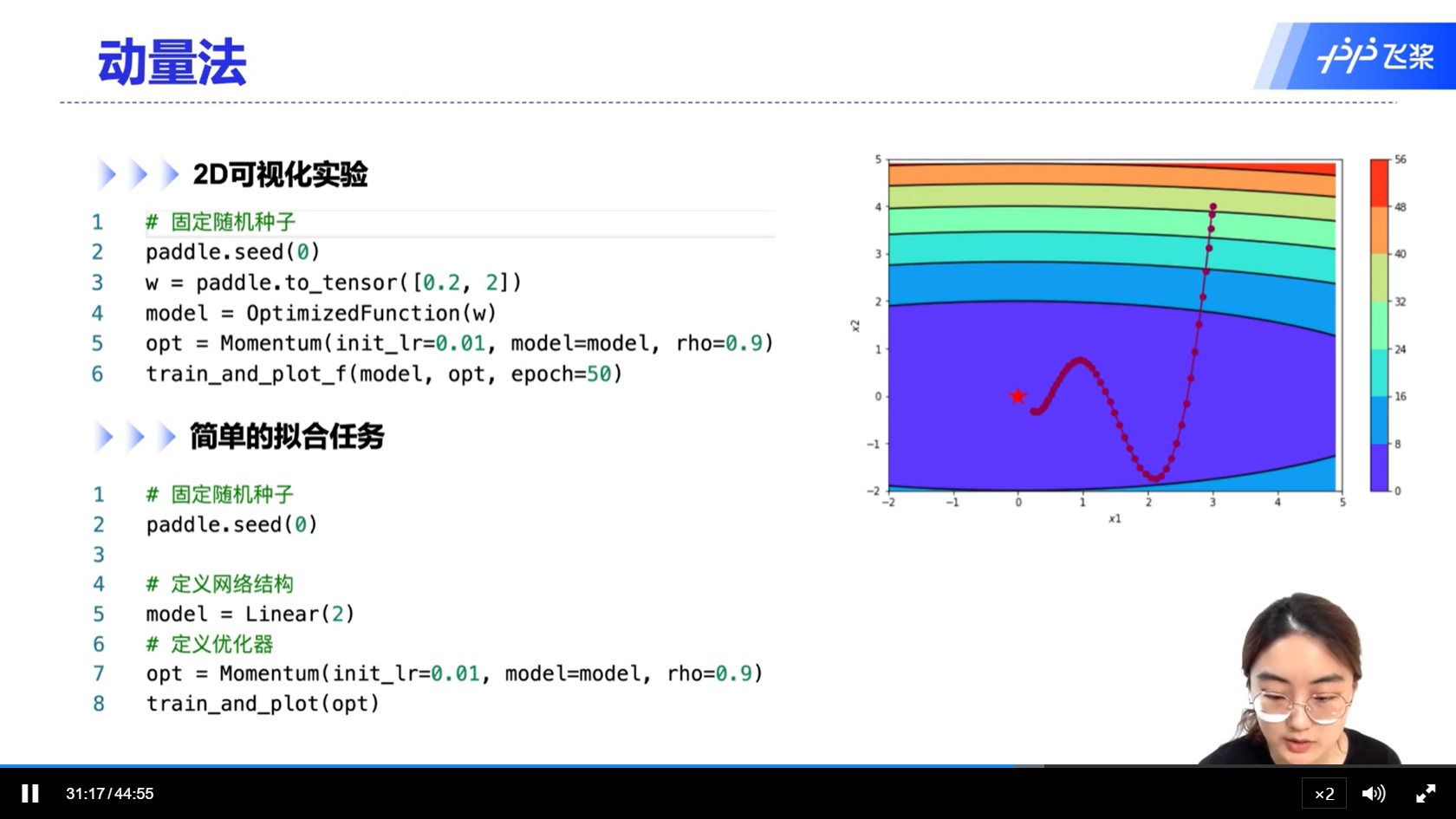
alec:
- 动量法:每次的梯度更新,都要考虑到前面一段时间的梯度,因此可以起到加速的作用

[√] Adam算法

alec:
- Adam算法,无需过度调参,收敛效果更好

alec:
- 两个参数0.9和0.99相当于是两个默认值了,默认情况下我们会选择这两个参数作为参数值
- AdamW算法是对adam算法的一个改进
[√] 不同优化算法的比较分析


[√] 不同优化器的3D可视化对比
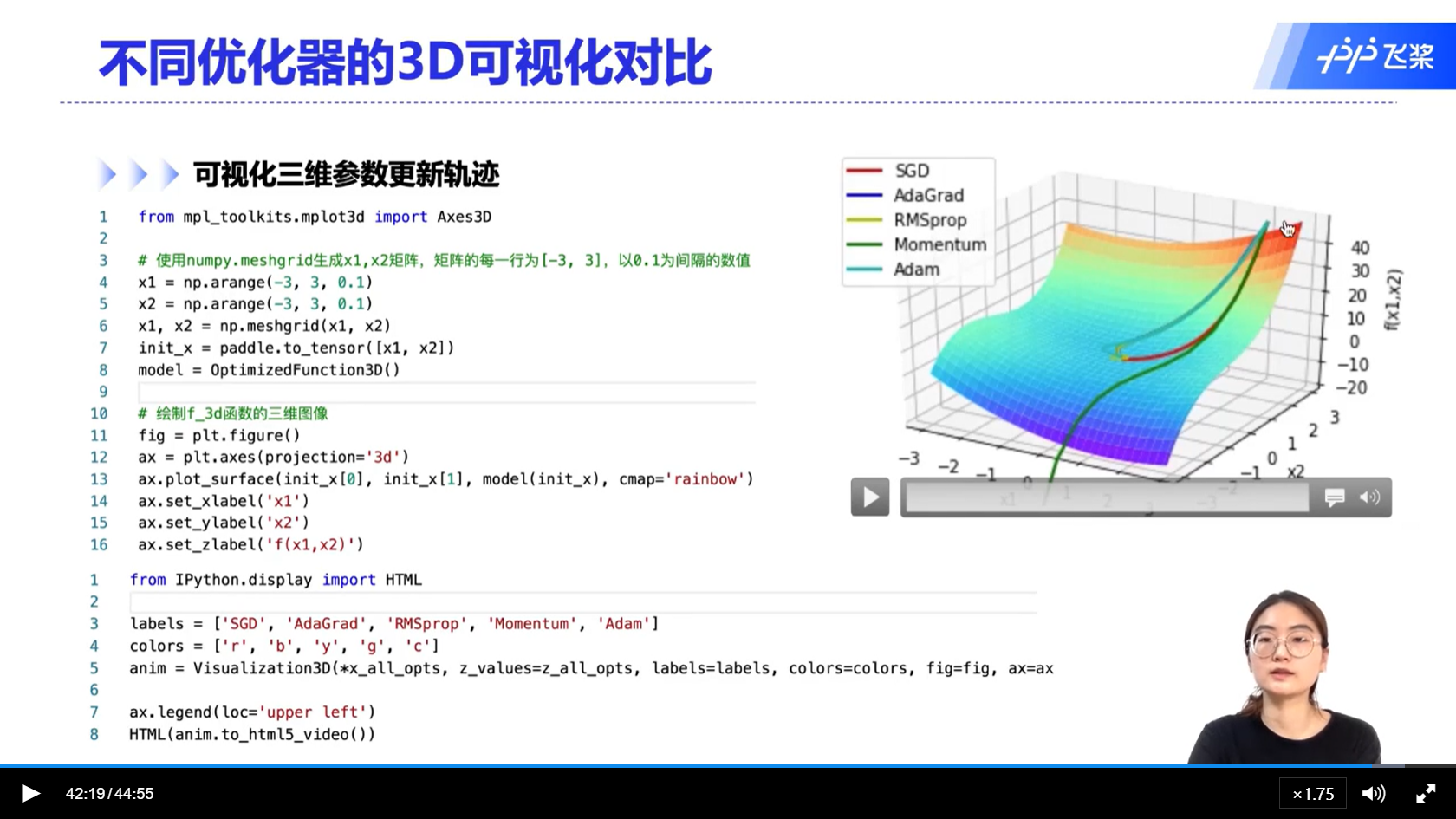
alec:
- 这个实验中,只有momentum优化器成功的逃离了鞍点
- 更考虑收敛速度和少调节参数的话,选择Adam优化器
- 需要更多的优化精度和人为的参数调节的话,优先考虑momentum优化器
[√] 7.4 - 参数初始化
[√] 参数初始化
alec:
- 基于方差缩放的初始化:为了防止梯度爆炸或者梯度消失,我们尽可能的保持每一个神经元的输入和输出的方差是一致的。根据每一层神经元的数量来自适应的调整输入输出的方差

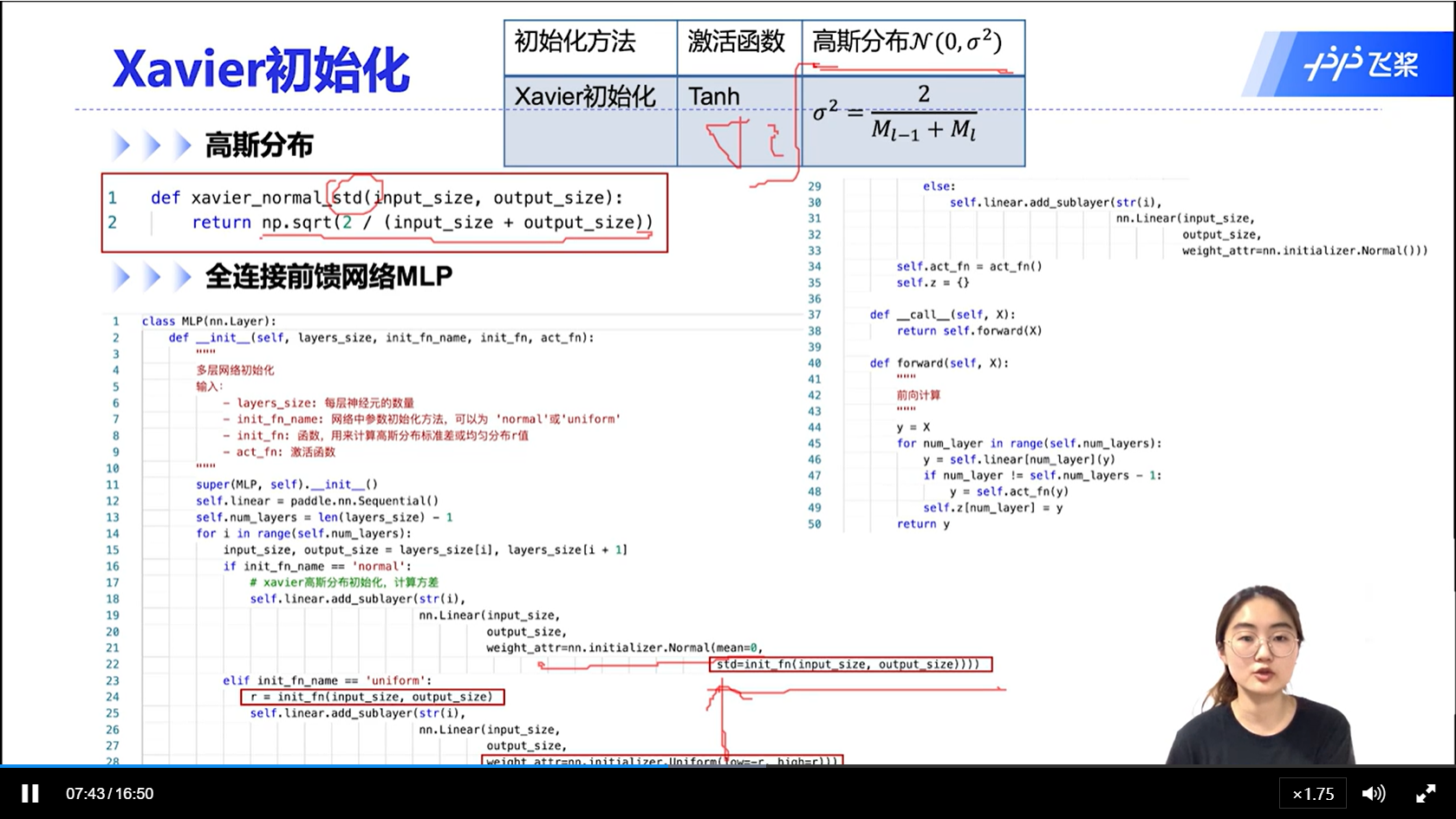
alec:
- std为标准差
[√] 实验验证神经网络的初始化是否会影响模型的收敛性
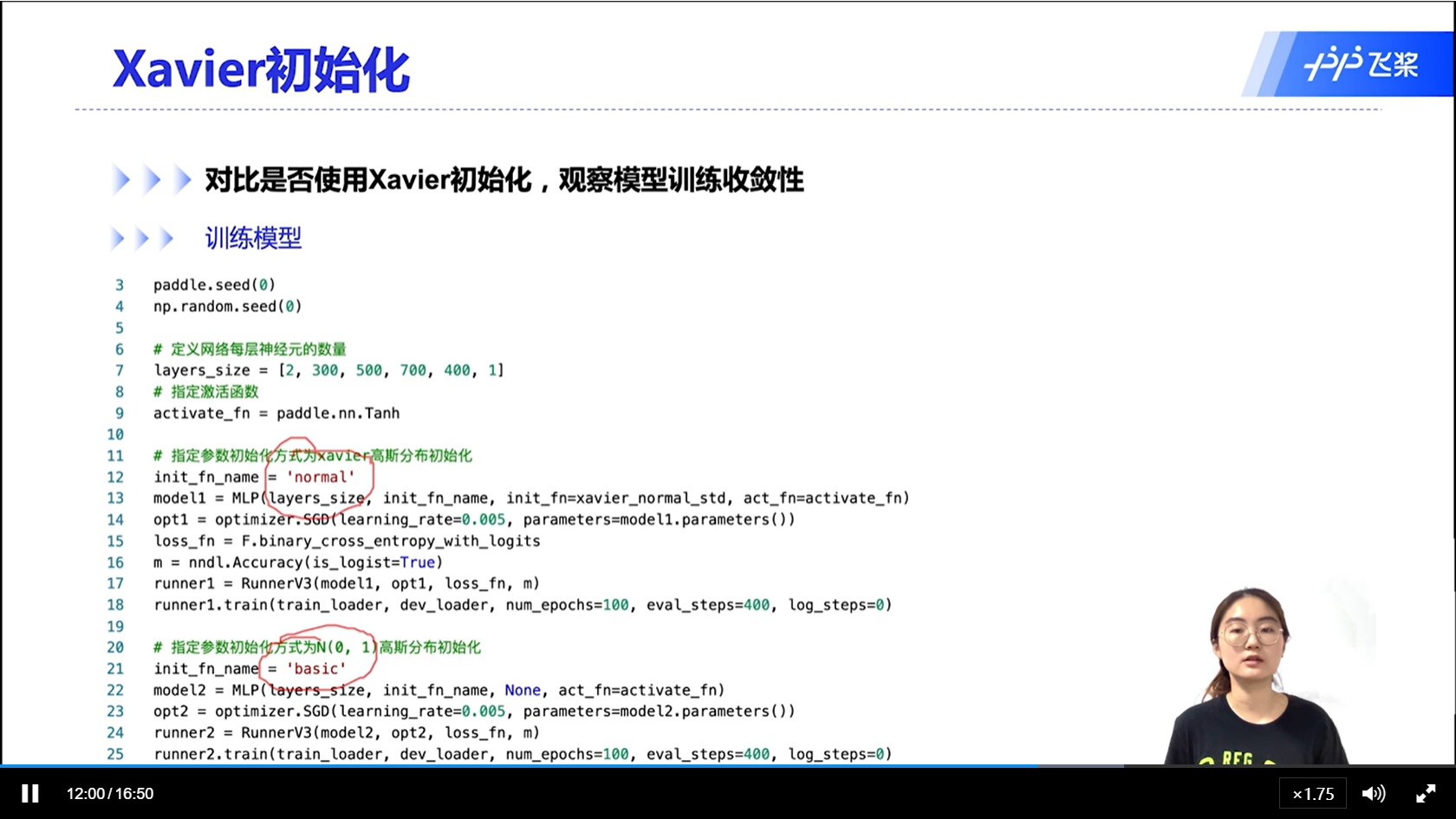
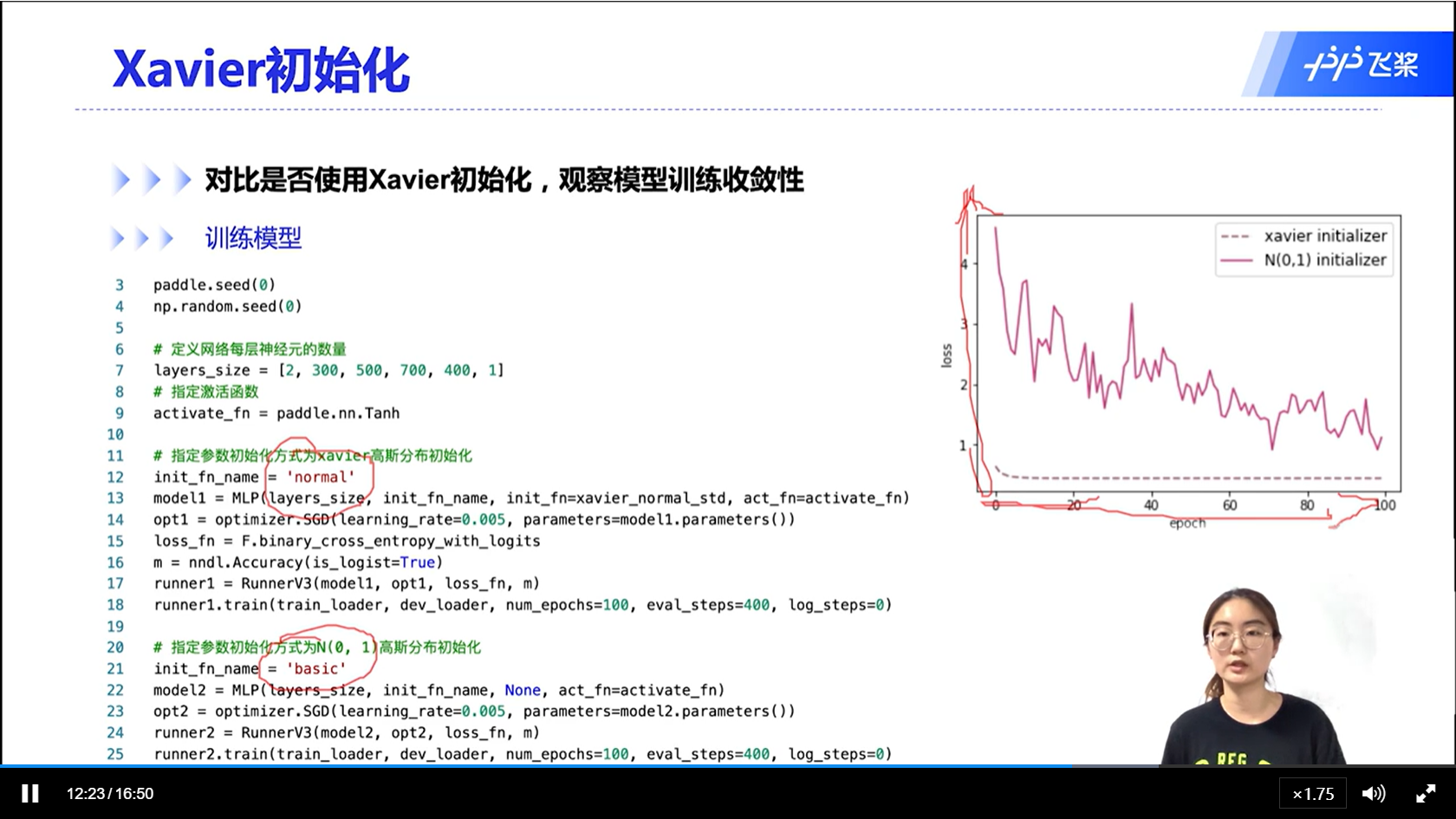
alec:
- 能够看出,基于方差缩放的参数初始化,能够更好的收敛
[√] 实际训练中的初始化
alec:
- 实际情况中,一般会选择一个在大规模数据上训练过的模型的参数作为初始化参数
[√] 7.5 - 逐层规范化
[√] 逐层规范化
alec:
- 逐层规范化是为了缓解模型训练过程中发生的内部协变量偏移问题。模型的高层和底层训练的速度不一样,当模型的数据分布发生变化的时候,就会产生内部协变量偏移问题。
- 逐层规范化之后,每一层的数据分布是统一的,因此不会发生因为数据的分布发生变化导致模型的参数需要重新拟合的现象。
[√] 批量规范化
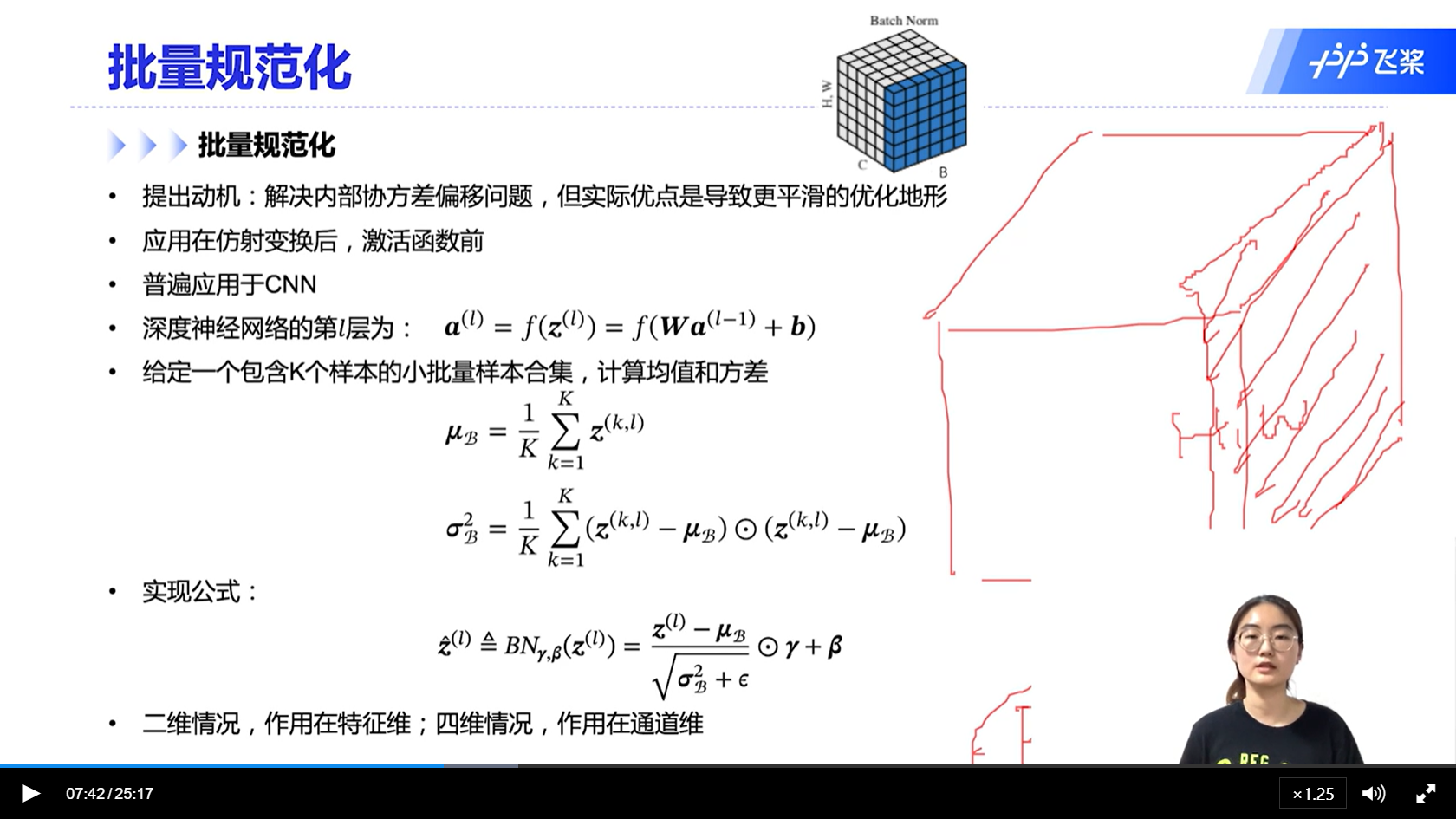
alec:
- BN用在仿射函数后,激活函数前
- BN提出的目的是解决内部协变量偏移问题,但是实际优点是可以让模型有更平滑的优化地形
- BN普遍应用于CNN
alec:
- 在测试的时候如何批量规范化?
- 在训练的时候,保存整个训练的均值和方差的移动平均值,测试和评估的时候,使用移动平均值进行BN。
[√] 内部协变量偏移实验

[√] 验证BN的有效性
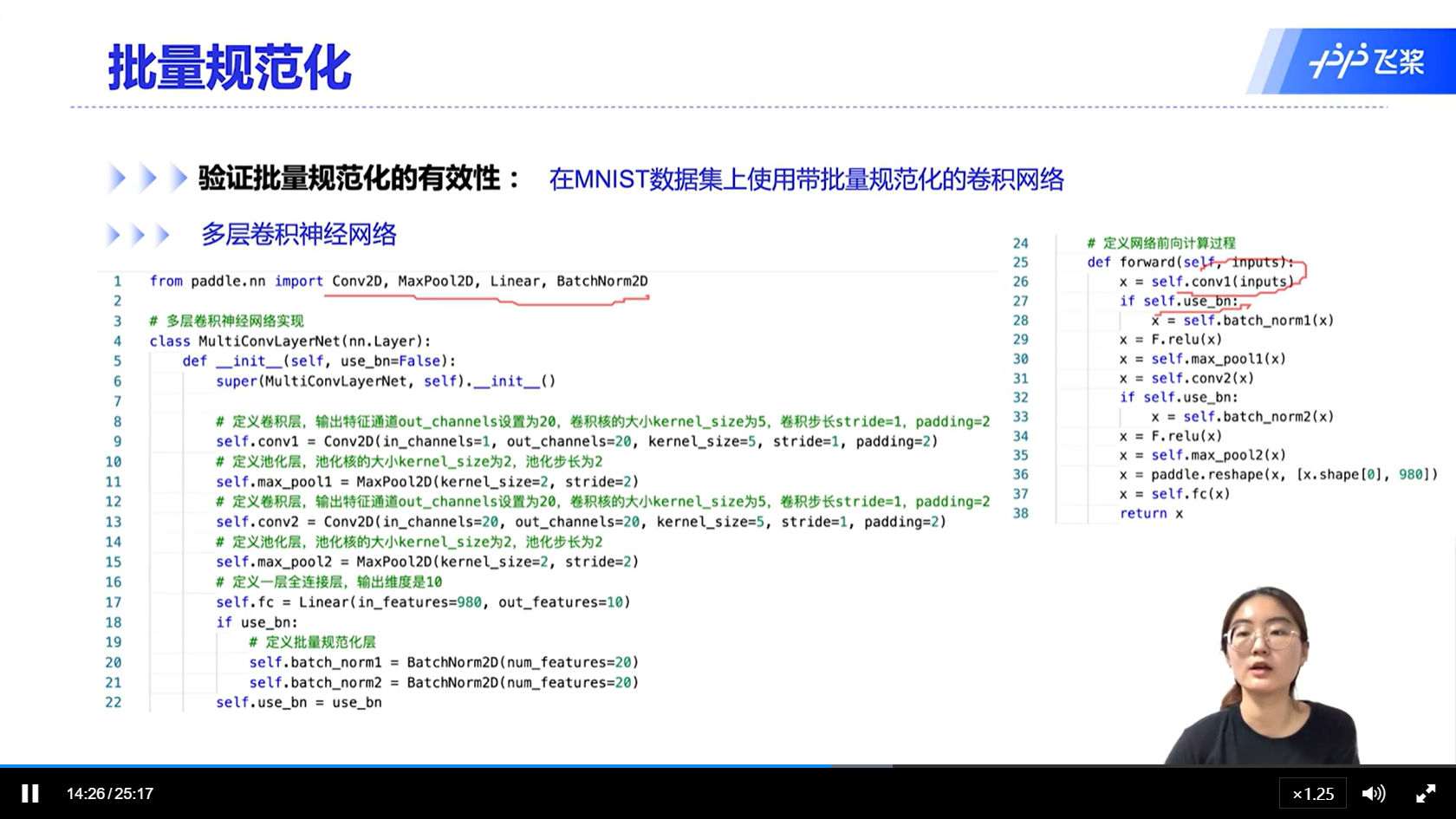
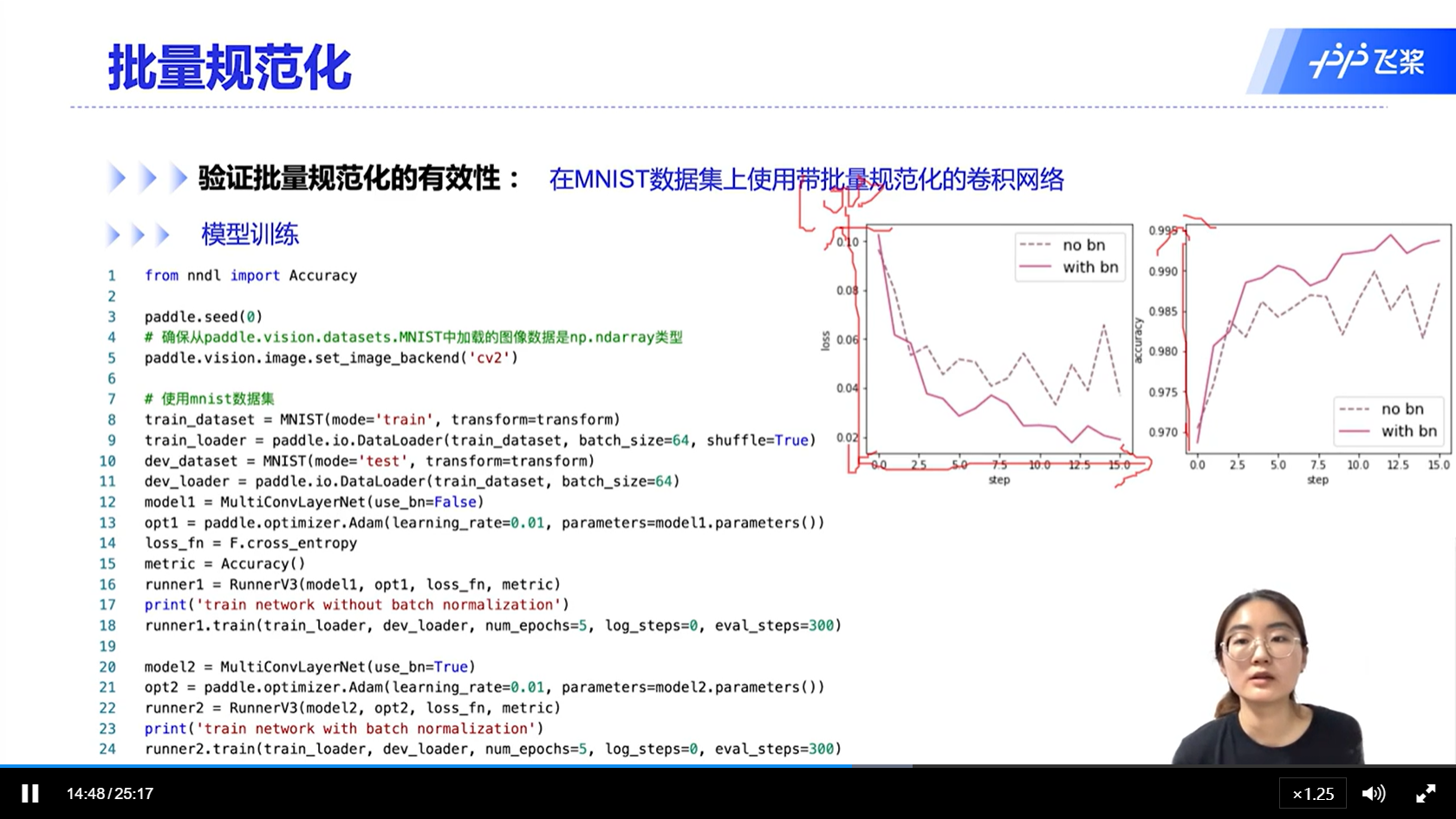
alec:
- 可以看出,带BN的模型,收敛效果和准确率均有所提升
[√] 层规范化

alec:
- 层规范化普遍应用于NLP,批量规范化普遍应用于CV
- 层规范化不分训练模式和测试模式,因为层规范化不基于样本的数量。BN分训练模式和测试模式,因为测试和预测的时候,数据可能就1张,不是一个batch,因为无法求得靠谱的均值和方差,因此在测试模式的时候,BN使用训练的时候的移动平均的均值和方差来进行BN。


[√] 7.6 - 网络正则化

[√] 网络正则化
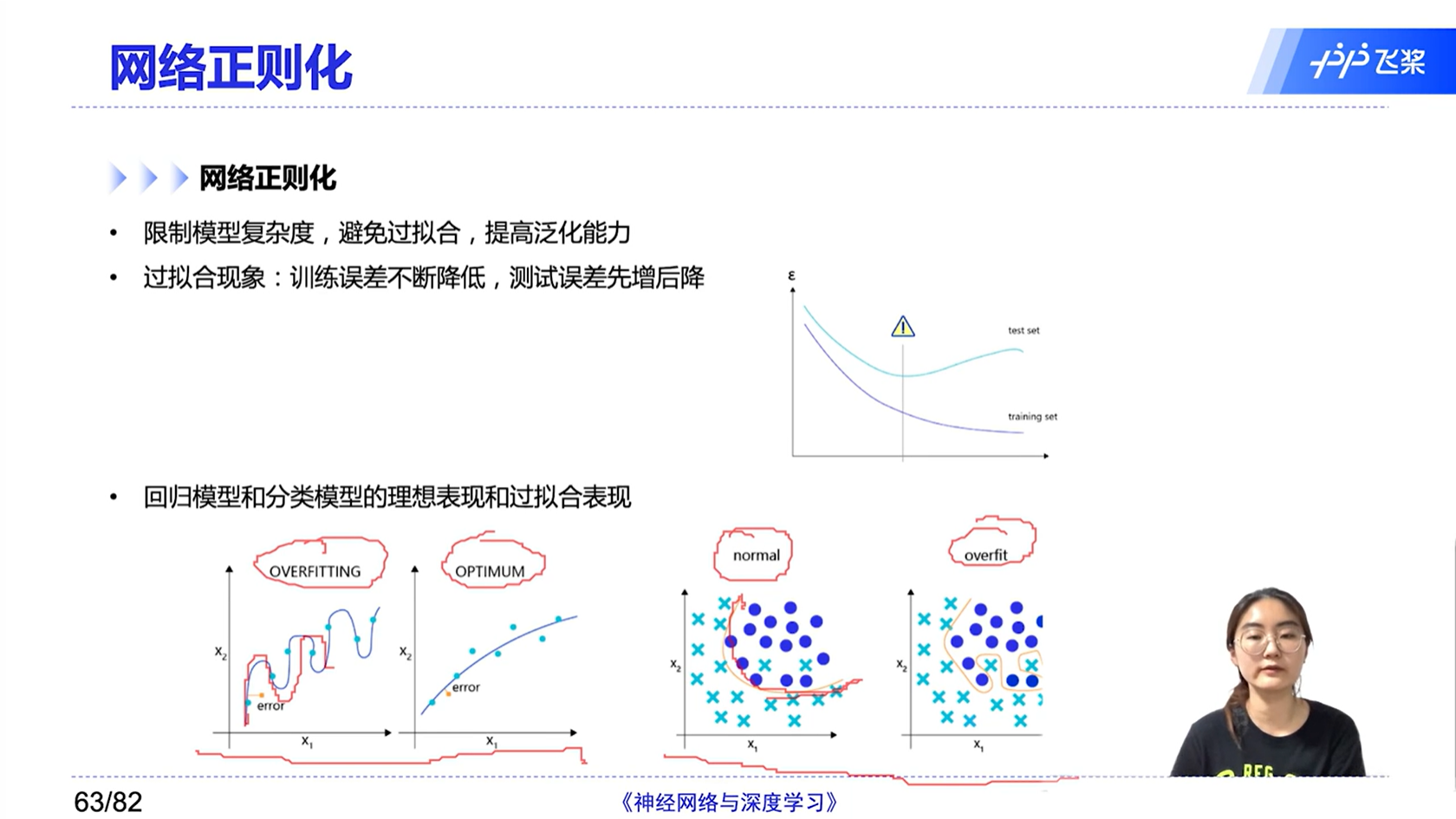
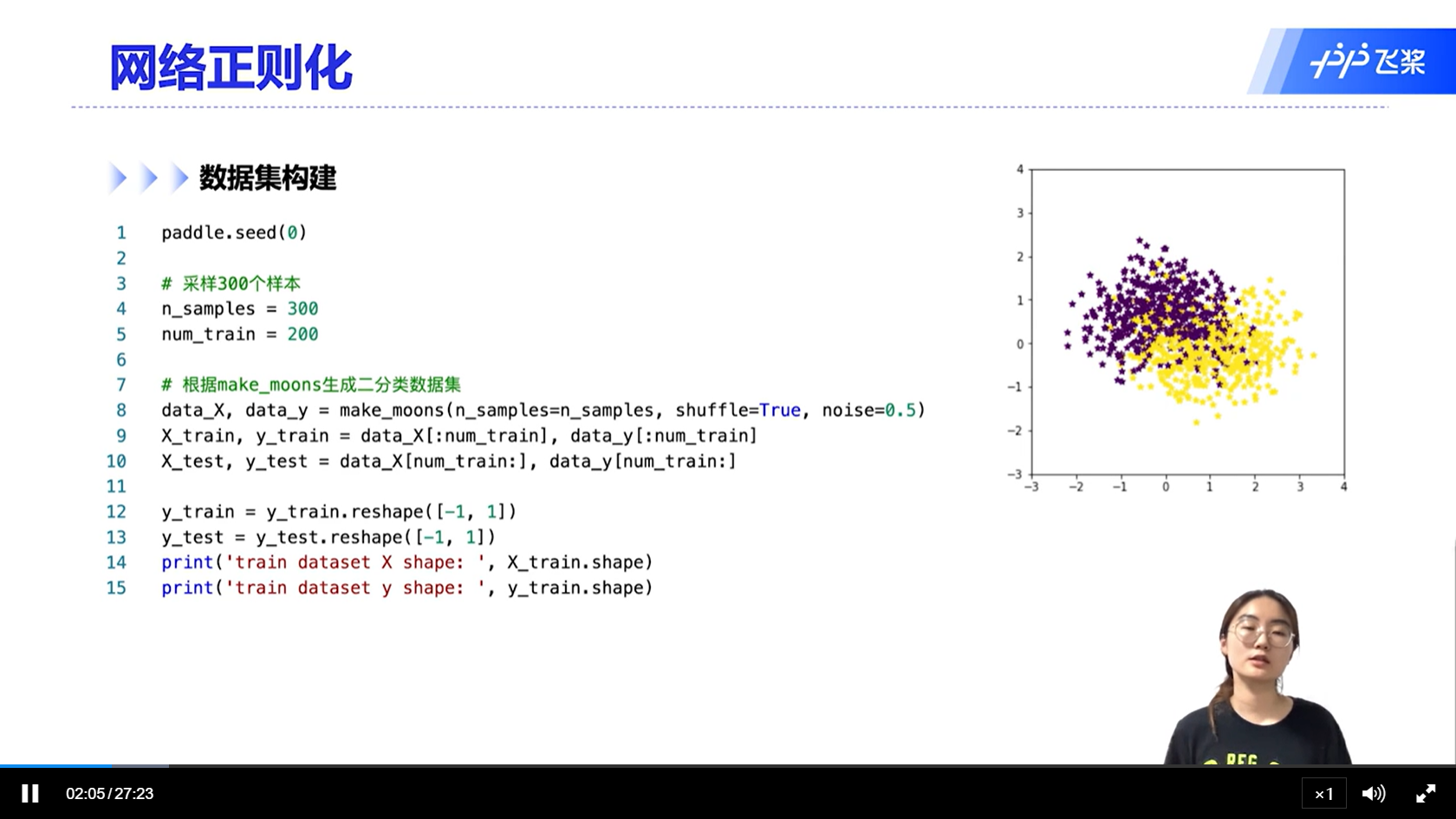



[√] L2正则化
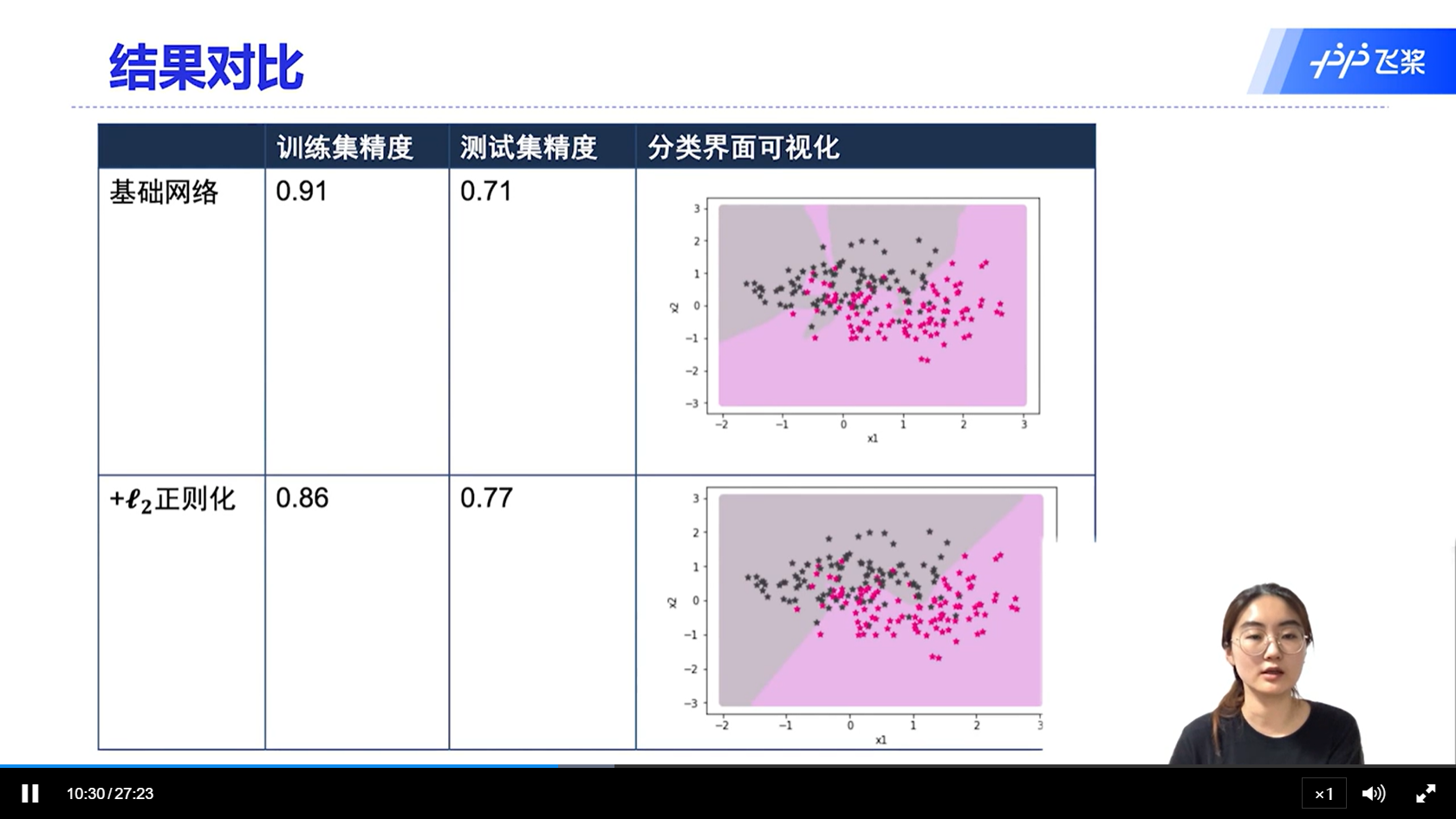
[√] 权重衰减

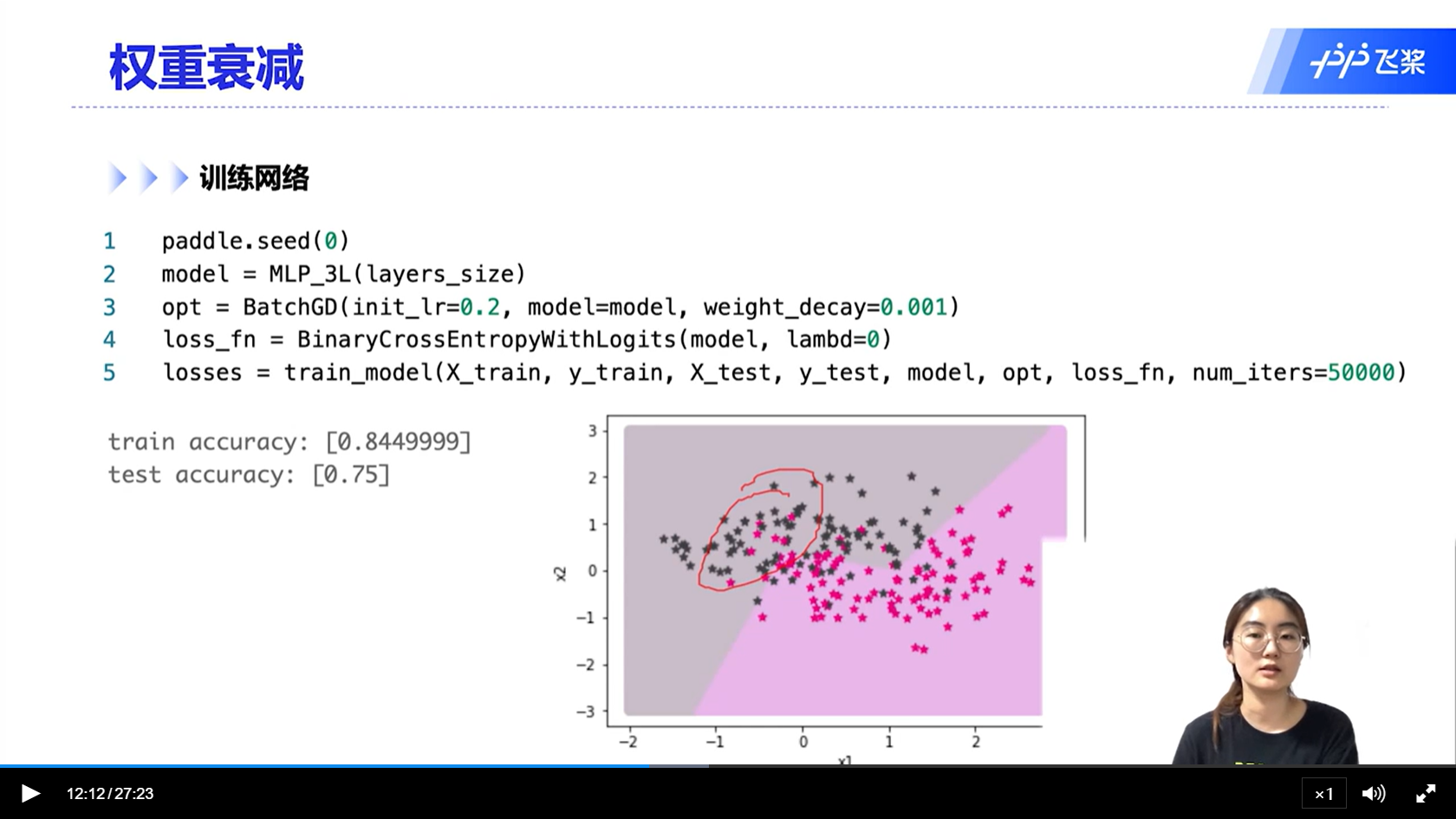
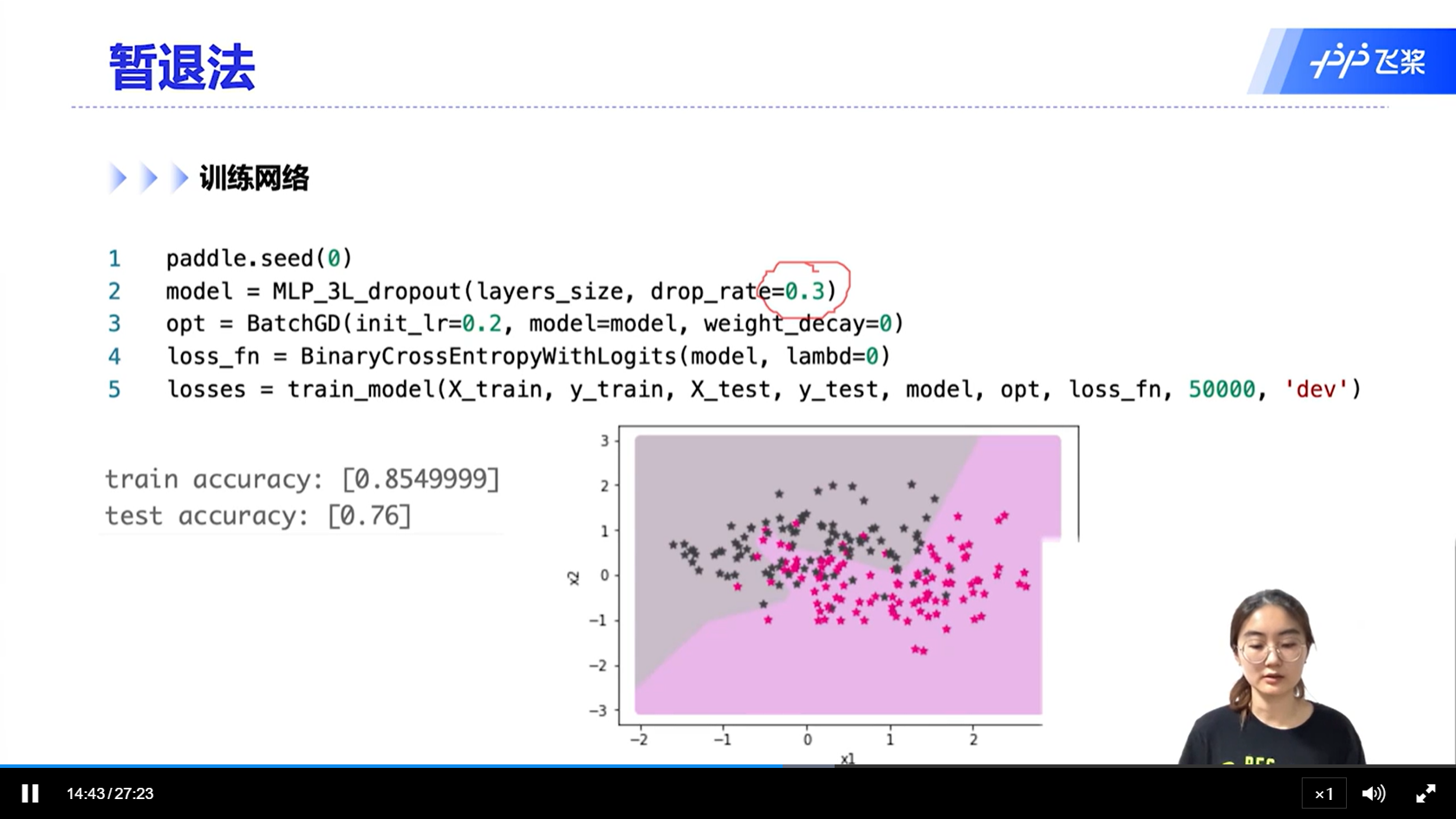
[√] 暂退法
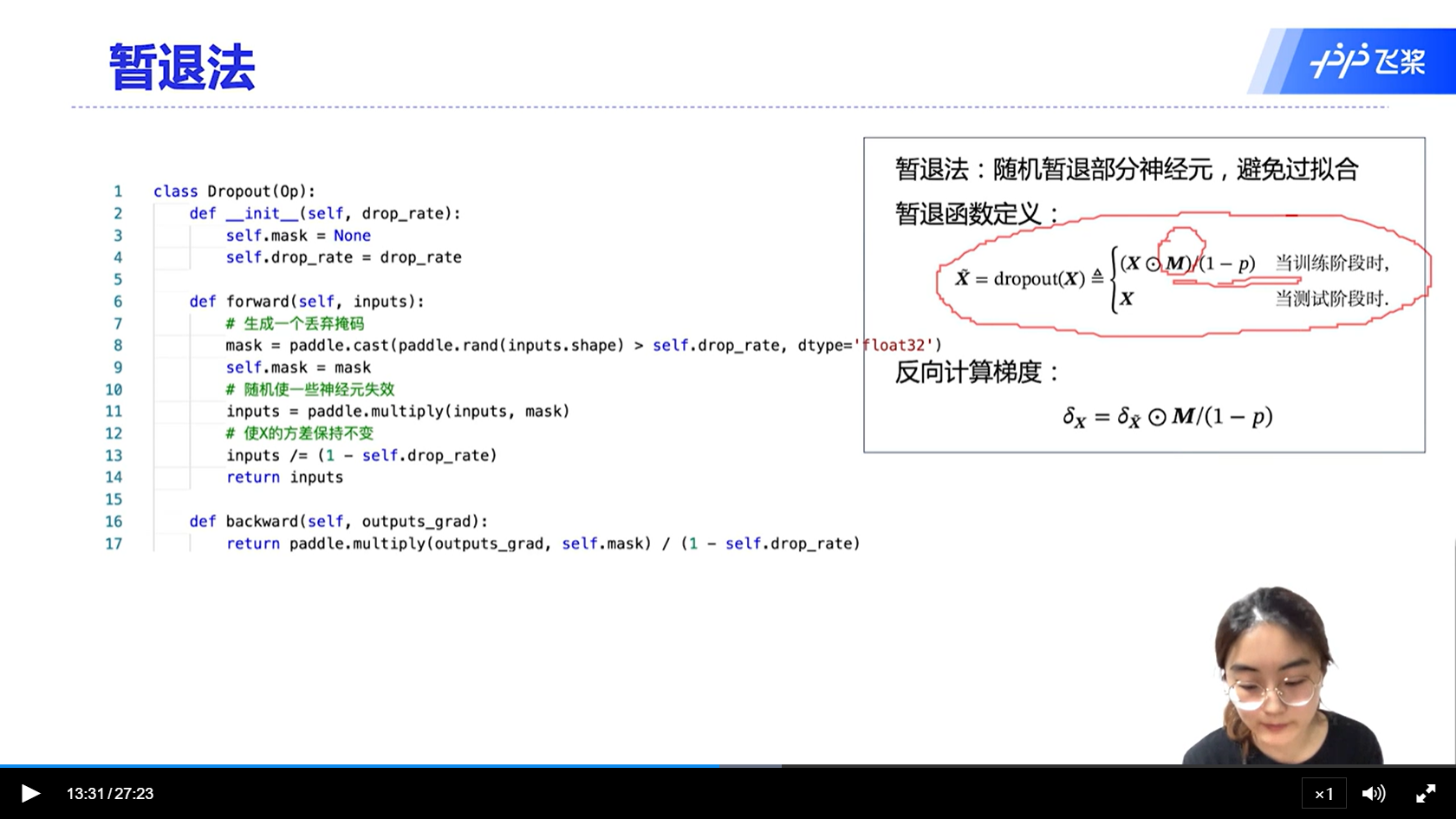
alec:
- 因为测试阶段没有暂退,所以会导致协变量偏移问题。为了解决这个问题,在训练阶段如上图所示,对神经元的值除以(1-p),这样保证训练阶段和测试阶段的方法是一致的。
- BN在激活函数之前
- dropout在激活函数之后
- 测试的时候,有BN,使用训练时的移动平均的均值和方差
- 测试的时候,不使用dropout
- dropout rate是将一个神经元的概率置为0的概率
[√] 实际训练中的正则化
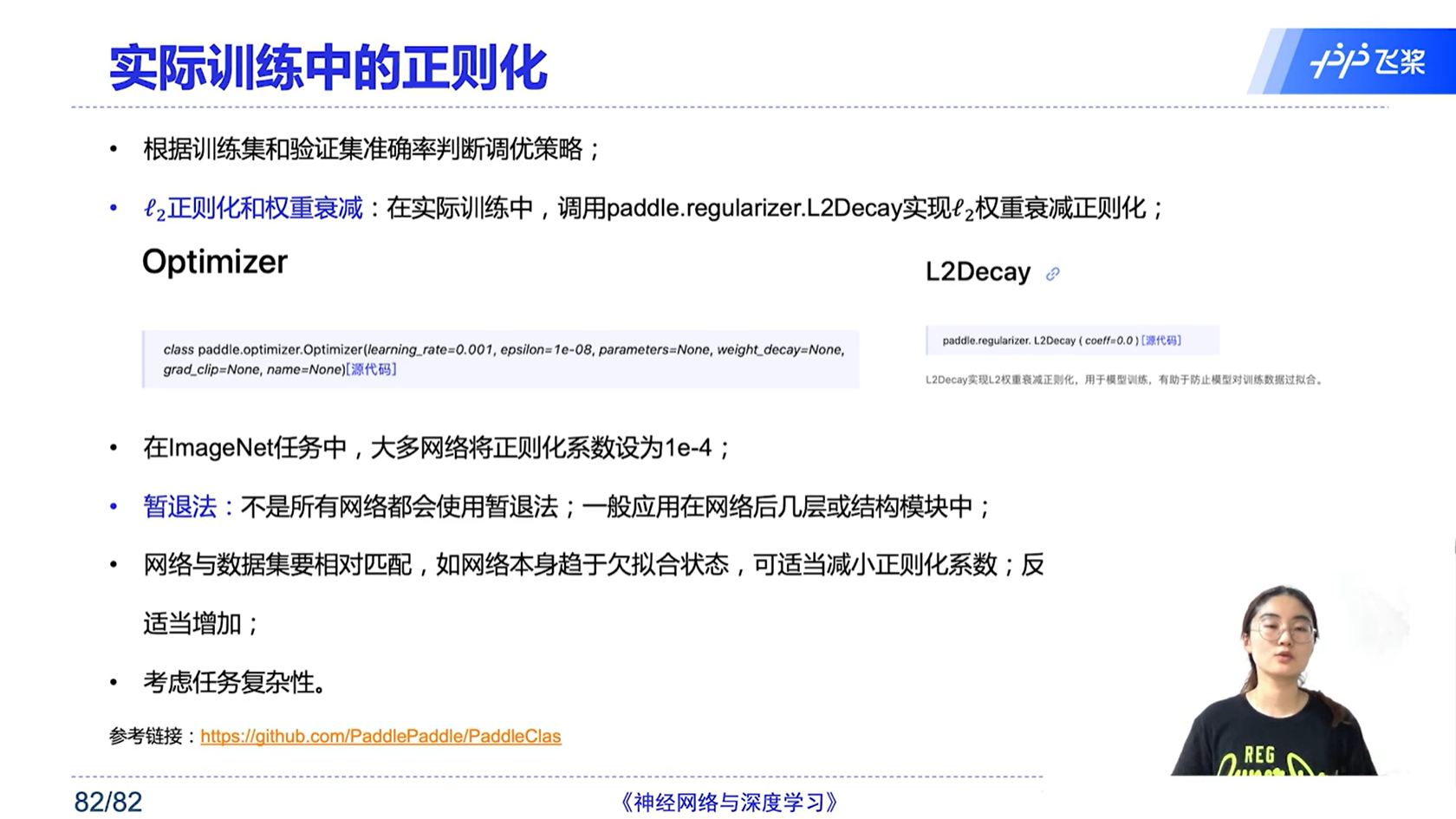
alec:
- 权重衰减是在参数的更新的时候发生的。衰减的是权重、也就是参数。
- x = x - αg
- x = (1 - β)x - αg <—-权重衰减
7 - 网络优化与正则化 - 视频
https://alec-97.github.io/posts/3380835339/