7 - 网络优化与正则化 - 书籍3

本文最后更新于：3 个月前

[√] 7.6 网络正则化方法

alec：

  • 神经网络很深，拟合能力很强，很容易就在训练集上过拟合，因此需要一定的手段来惩罚网络参数的更新。正则化就是惩罚网络参数更新，防止过拟合的方法。
  • 由于深度神经网络的复杂度比较高，并且拟合能力很强，很容易在训练集上产生过拟合，因此在训练深度神经网络时，也需要通过一定的正则化方法来改进网络的泛化能力。
  • 正则化（Regularization）是一类通过限制模型复杂度，从而避免过拟合、提高泛化能力的方法，比如引入约束、增加先验、提前停止等。
  • 提前停止、引入约束、增加先验，都是正则化的方法

为了展示不同正则化方法的实现方式和效果，本节构建一个小数据集和多层感知器来模拟一个过拟合的实验场景，并实现ℓ2正则化、权重衰减和暂退法，观察这些正则化方法是否可以缓解过拟合现象。

alec：

  • L_2正则化、权重衰减、暂退法都是正则化的方法

[√] 7.6.1 数据集构建

首先使用数据集构建函数make_moons来构建一个小的数据集，生成300个样本，其中200个作为训练数据，100个作为测试数据。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
paddle.seed(0)

# 采样300个样本
n_samples = 300
num_train = 200

# 根据make_moons生成二分类数据集
data_X, data_y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)
X_train, y_train = data_X[:num_train], data_y[:num_train]
X_test, y_test = data_X[num_train:], data_y[num_train:]

y_train = y_train.reshape([-1, 1])
y_test = y_test.reshape([-1, 1])
print('train dataset X shape: ', X_train.shape)
print('train dataset y shape: ', y_train.shape)
print(X_train[0])
1
2
3
4
train dataset X shape:  [200, 2]
train dataset y shape:  [200, 1]
Tensor(shape=[2], dtype=float32, place=CUDAPlace(0), stop_gradient=True,
       [-0.45755064, -0.99871635])

[√] 7.6.2 模型构建

为了更好地展示正则化方法的实现机理，本节使用本书自定义的Op类来构建一个全连接前馈网络（即多层感知器）MLP_3L。MLP_3L是一个三层感知器，使用ReLU激活函数，最后一层输出层为线性层，即输出对率。

首先，我们实现ReLU算子，然后复用第4.2.4.4节中定义的Linear算子，组建多层感知器MLP_3L。

[√] 7.6.2.1 ReLU算子

假设一批样本组成的矩阵$Z \in \mathbb{R}^{N\times D}$，每一行表示一个样本，$N$为样本数，$D$为特征维度，ReLU激活函数的前向过程表示为
$$
A=\max( Z,0)\in \mathbb{R}^{N\times D},
$$
其中$A$为经过ReLU函数后的活性值。

令$\delta_{ A}=\frac{\partial \mathcal{R}}{\partial A}\in \mathbb{R}^{N\times D}$表示最终损失$\mathcal{R}$对ReLU算子输出$ A$的梯度，ReLU激活函数的反向过程可以写为
$$
\delta_{ Z} = \delta_{ A}\odot( A>0) \in \mathbb{R}^{N\times D},
$$
其中$\delta_{Z}$为ReLU算子反向函数的输出。

下面实现的ReLU算子，并实现前向和反向的计算。由于ReLU函数中没有参数，这里不需要在backward()方法进一步计算该算子参数的梯度。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class ReLU(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        self.inputs = inputs
        return paddle.multiply(inputs, paddle.to_tensor(inputs > 0, dtype='float32'))

    def backward(self, outputs_grads):
        #计算ReLU激活函数对输入的导数
        # paddle.multiply是逐元素相乘算子
        return paddle.multiply(outputs_grads, paddle.to_tensor(self.inputs > 0, dtype='float32'))
[√] 7.6.2.2 自定义多层感知器

alec：

  • 函数backward进行网络的反向计算，将网络中参数梯度保存下来，后续通过优化器进行梯度更新。

这里，我们构建一个多层感知器MLP_3L。MLP_3L算子由三层线性网络构成，层与层间加入ReLU激活函数，最后一层输出层为线性层，即输出对率（logits）。复用Linear算子，结合ReLU算子，实现网络的前反向计算。初始化时将模型中每一层的参数$W$以标准正态分布的形式进行初始化，参数$b$初始化为0。函数forward进行网络的前向计算，函数backward进行网络的反向计算，将网络中参数梯度保存下来，后续通过优化器进行梯度更新。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import nndl.op as op

class MLP_3L(Op):
    def __init__(self, layers_size):
        self.fc1 = op.Linear(layers_size[0], layers_size[1], name='fc1')
        # ReLU激活函数
        self.act_fn1 = ReLU()
        self.fc2 = op.Linear(layers_size[1], layers_size[2], name='fc2')
        self.act_fn2 = ReLU()
        self.fc3 = op.Linear(layers_size[2], layers_size[3], name='fc3')
        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2, self.fc3]

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        z3 = self.fc3(a2)
        return z3

    def backward(self, loss_grad_z3):
        loss_grad_a2 = self.fc3.backward(loss_grad_z3)
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)
[√] 7.6.2.3 损失函数算子

使用交叉熵函数作为损失函数。这里MLP_3L模型的输出是对率而不是概率，因此不能直接使用第4.2.3节实现的BinaryCrossEntropyLoss算子。我们这里对交叉熵函数进行完善，使其可以直接接收对率计算交叉熵。

alec：

  • 模型的输出，经过激活函数之后，才得到位于0-1范围的概率

对二分类交叉熵损失进行改写，令向量$y\in {0,1}^N$表示$N$个样本的标签构成的向量，向量$ o\in \mathbb{R}^N$表示$N$个样本的模型输出的对率，二分类的交叉熵损失为

$$
\mathcal{R}( y, o) = -\frac{1}{N}( y^{T} \log \sigma( o) + (1 - y)^{T} \log(1-\sigma( o))),
$$

其中$\sigma$为Logistic函数。

二分类交叉熵损失函数的输入是神经网络的输出$ o$。最终的损失$\mathcal{R}$对$ o$的偏导数为:
$$
\frac{\partial \mathcal R}{\partial o} = -\frac{1}{N}( y-\sigma( o)).
$$

损失函数BinaryCrossEntropyWithLogits的代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class BinaryCrossEntropyWithLogits(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.data_size = None
        self.model = model
        self.logistic = op.Logistic()

    def __call__(self, logits, labels):
        return self.forward(logits, labels)

    def forward(self, logits, labels):
        # 输入先经过激活函数
        self.predicts = self.logistic(logits)
        self.labels = labels
        self.data_size = self.predicts.shape[0]
        loss = -1. / self.data_size * (paddle.matmul(self.labels.t(), paddle.log(self.predicts)) + paddle.matmul((1 - self.labels.t()), paddle.log(1 - self.predicts)))
        loss = paddle.squeeze(loss, axis=1)
        # 返回损失
        return loss

    def backward(self):
        # 计算输出对输入的损失
        inputs_grads = 1./ self.data_size * (self.predicts - self.labels)
        self.model.backward(inputs_grads)

定义accuracy_logits函数，输入为logits和labels。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def accuracy_logits(logits, labels):
    """
    输入:
        - logits: 预测值，二分类时，shape=[N, 1]，N为样本数量; 多分类时，shape=[N, C]，C为类别数量
        - labels: 真实标签，shape=[N, 1]
    输出:
        - 准确率: shape=[1]
    """
    # 判断是二分类任务还是多分类任务，preds.shape[1]=1时为二分类任务，preds.shape[1]>1时为多分类任务
    if logits.shape[1] == 1:
        # 二分类时，判断每个logits是否大于0，当大于0时类别为1，否则类别为0
        #使用'paddle.cast'将preds的数据类型转换为float32类型
        preds = paddle.cast((logits > 0), dtype='float32')
    else:
        # 多分类时，使用'paddle.argmax'计算最大元素索引作为类别
        preds = paddle.argmax(logits, axis=1, dtype='int32')
    return paddle.mean(paddle.cast(paddle.equal(preds, labels), dtype='float32'))
1
2
运行时长: 5毫秒
结束时间: 2022-12-25 18:10:37
[√] 7.6.2.4 模型训练

使用train_model函数指定训练集数据和测试集数据、网络、优化器、损失函数、训练迭代次数等参数。代码实现如下：

alec：

  • Normalization翻译为规范化、Dropout翻译为暂退法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def train_model(X_train, y_train, X_test, y_test, model, optimizer, loss_fn, num_iters, *args):
    """
    训练模型
    输入：
        - X_train, y_train: 训练集数据
        - X_test, y_test: 测试集数据
        - model: 定义网络
        - optimizer: 优化器
        - loss_fn: 损失函数
        - num_iters: 训练迭代次数
        - args: 在dropout中指定模型为训练模式或评价模式
    """
    losses = []
    for i in range(num_iters):
        # 前向计算
        train_logits = model(X_train)
        loss = loss_fn(train_logits, y_train)
        # 反向计算
        loss_fn.backward()
        # 更新参数
        optimizer.step()
        if i % 100 == 0:
            losses.append(loss)

    train_logits = model(X_train, *args)
    acc_train = accuracy_logits(train_logits, y_train)
    test_logits = model(X_test, *args)
    acc_test = accuracy_logits(test_logits, y_test)
    print('train accuracy:', acc_train.numpy())
    print('test accuracy:', acc_test.numpy())
    return losses
1
2
运行时长: 6毫秒
结束时间: 2022-12-25 20:50:58

复用第4.2.4.6节中的BatchGD定义梯度下降优化器。进行50 000次训练迭代，观察模型在训练集和测试集上的准确率。代码实现如下：

1
2
3
4
5
6
7
8
from nndl.op import BatchGD

paddle.seed(0)
layers_size = [X_train.shape[1], 20, 3, 1]
model = MLP_3L(layers_size)
opt = BatchGD(init_lr=0.2, model=model)
loss_fn = BinaryCrossEntropyWithLogits(model)
losses = train_model(X_train, y_train, X_test, y_test, model, opt, loss_fn, 50000)
1
2
train accuracy: [0.91]
test accuracy: [0.7099999]

从输出结果看，模型在训练集上的准确率为91%，在测试集上的准确率为71%，推断模型出现了过拟合现象。为了更好地观察模型，我们通过可视化分类界面来确认模型是否发生了过拟合。

可视化函数show_class_boundary的代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def show_class_boundary(model, X_train, y_train, *args, fig_name):
    #均匀生成40 000个数据点
    x1, x2 = paddle.meshgrid(paddle.linspace(-2, 3, 200), paddle.linspace(-3, 3, 200))
    x = paddle.stack([paddle.flatten(x1), paddle.flatten(x2)], axis=1)
    #预测对应类别
    y = model(x, *args)
    y = paddle.cast((y>0), dtype='int32').squeeze()

    bg_colors = ['#f5f5f5' if y==1 else '#f19ec2' for y in y]
    label_colors = ['#000000' if train_label==0 else '#e4007f' for train_label in y_train]

    #绘制类别区域
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.scatter(x[:, 0].numpy(), x[:, 1].numpy(), c=bg_colors)
    plt.scatter(X_train[:, 0].numpy(), X_train[:, 1].numpy(), marker='*', c=label_colors)
    plt.savefig(fig_name)
1
show_class_boundary(model, X_train, y_train, fig_name='opti-regularization.pdf')

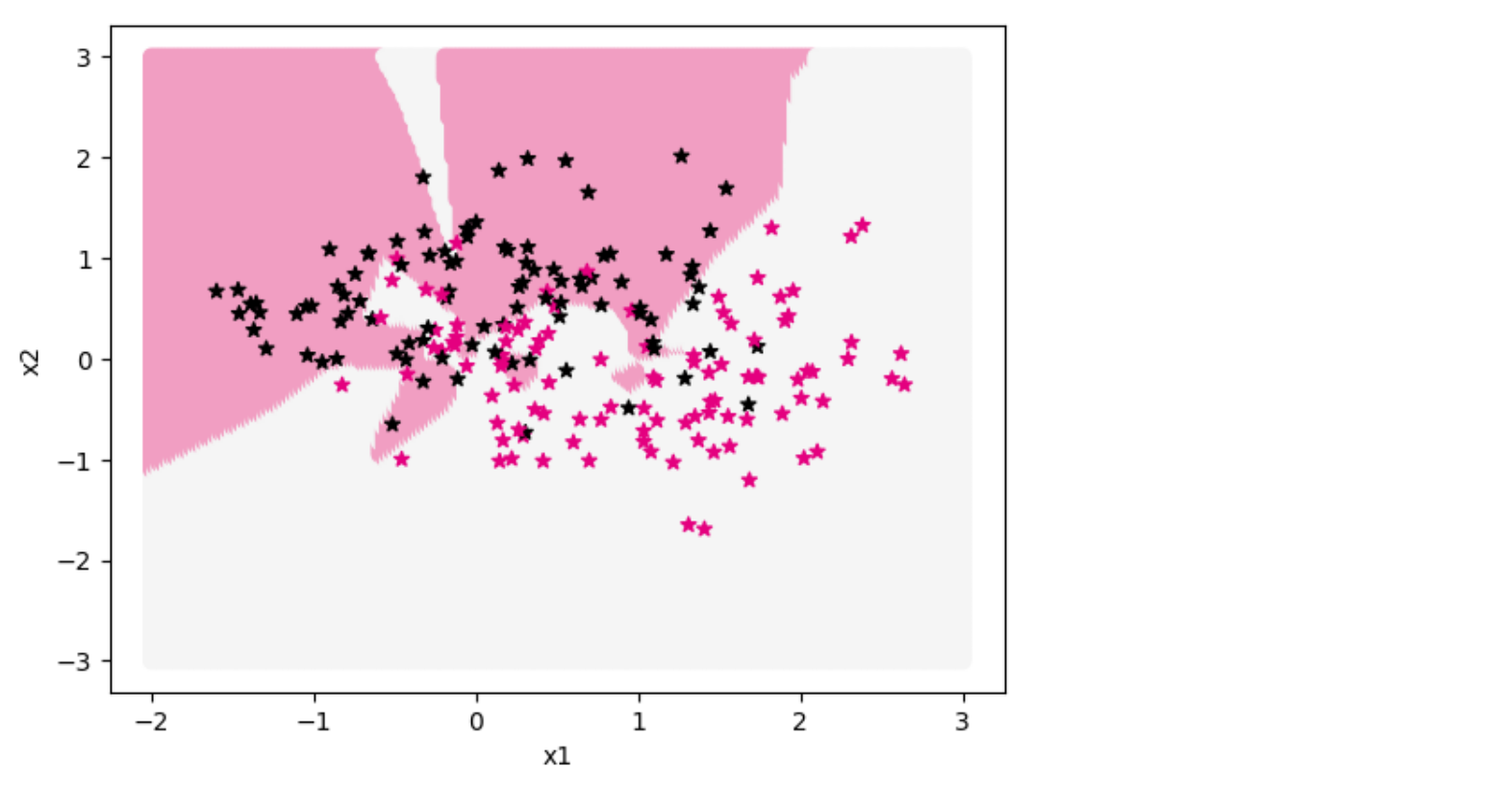
image-20221225205822948

图中两种颜色的点代表两种类别的分类标签，不同颜色的区域是模型学习到的两个分类区域。从输出结果看，交界处的点被极细致地进行了区域分割，说明模型存在过拟合现象。

[√] 7.6.3 ℓ_1和ℓ_2正则化

alec：

  • $\ell_1$和$\ell_2$正则化是机器学习中最常用的正则化方法

  • 通过约束参数的$\ell_1$和$\ell_2$范数来减小模型在训练数据集上的过拟合现象（正则化用来减小过拟合现象）

  • 通过加入$\ell_1$和$\ell_2$正则化，优化问题可以写为
    $$
    \theta^{*} = \mathop{\arg\min}\limits_{\theta} \frac{1}{B} \sum_{n=1}^{B} \mathcal{L}(y^{(n)}, f( x^{(n)};\theta)) + \lambda \ell_p(\theta),
    $$
    其中$\mathcal{L}(\cdot)$为损失函数，$B$为批量大小，$f(\cdot)$为待学习的神经网络，$\theta$为其参数，$\ell_p$为范数函数，$p$的取值通常为1,2代表$\ell_1$和$\ell_2$范数，$\lambda$为正则化系数。

  • 在交叉熵损失基础上增加$\ell_2$正则化，相当于前向计算时，损失加上$\frac{1}{2}|\theta|^2$。而反向计算时，所有参数的梯度再额外加上$\lambda\theta$。

  • 正则化就是在计算损失的时候，在损失函数上加上惩罚项，也就是正则项。L_2正则化，就是加上0.5θ^2^

下面通过实验来验证$\ell_2$正则化缓解过拟合的效果。在交叉熵损失基础上增加$\ell_2$正则化，相当于前向计算时，损失加上$\frac{1}{2}|\theta|^2$。而反向计算时，所有参数的梯度再额外加上$\lambda\theta$。

完善算子BinaryCrossEntropyWithLogits，使其支持带$\ell_2$正则化的损失函数。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class BinaryCrossEntropyWithLogits(Op):
    def __init__(self, model, lambd):
        self.predicts = None
        self.labels = None
        self.data_size = None
        self.model = model
        self.logistic = op.Logistic()
        self.lambd = lambd

    def __call__(self, logits, labels):
        return self.forward(logits, labels)

    def forward(self, logits, labels):
        self.predicts = self.logistic(logits)
        self.labels = labels
        self.data_size = self.predicts.shape[0]
        loss = -1. / self.data_size * (paddle.matmul(self.labels.t(), paddle.log(self.predicts)) + paddle.matmul((1 - self.labels.t()), paddle.log(1 - self.predicts)))
        loss = paddle.squeeze(loss, axis=1)
        regularization_loss = 0
        for layer in self.model.layers:
            if isinstance(layer, op.Linear):
                regularization_loss += paddle.sum(paddle.square(layer.params['W']))
        loss += self.lambd * regularization_loss / (2 * self.data_size)
        return loss

    def backward(self):
        inputs_grads = 1./ self.data_size * (self.predicts - self.labels)
        self.model.backward(inputs_grads)
        #更新正则化项对应的梯度
        for layer in self.model.layers:
            if isinstance(layer, op.Linear) and isinstance(layer.grads, dict):
                layer.grads['W'] += self.lambd * layer.params['W'] / self.data_size
1
2
运行时长: 8毫秒
结束时间: 2022-12-25 21:15:55

重新训练网络，增加$\ell_2$正则化后再进行50 000迭代。代码实现如下：

1
2
3
4
5
paddle.seed(0)
model = MLP_3L(layers_size)
opt = BatchGD(init_lr=0.2, model=model)
loss_fn = BinaryCrossEntropyWithLogits(model, lambd=0.7)
losses = train_model(X_train, y_train, X_test, y_test, model, opt, loss_fn, num_iters=50000)
1
2
train accuracy: [0.8599999]
test accuracy: [0.77]

从输出结果看，在训练集上的准确率为86%，测试集上的准确率为77%。从输出结果看，猜测过拟合现象得到缓解。

alec：

  • 训练集准确率下降，测试集准确率上升，二者的插值减少，模型效果升高，过拟合现象减弱。

再通过可视化分类界面证实猜测结果，代码实现如下：

1
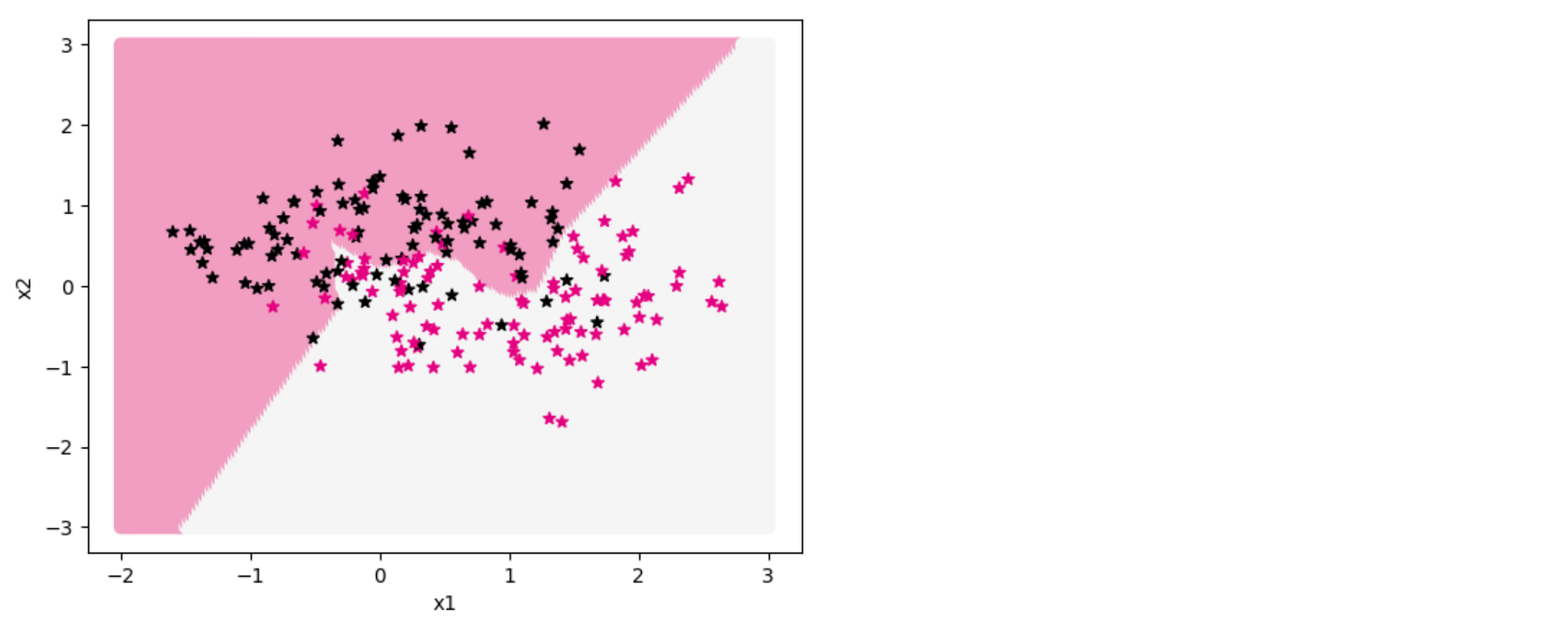
show_class_boundary(model, X_train, y_train, fig_name='opti-regularization2.pdf')

从输出结果看，过拟合现象有所缓解，说明$\ell_2$正则化可以缓解过拟合现象。

alec：

  • 问题记录：目前知道了L_1正则化和L_2正则化能够减少过拟合现象，但是具体为什么这种在损失函数中添加正则化项的方式能够减少过拟合还疑惑。

image-20221225212608299

[√] 7.6.4 权重衰减

alec：

  • 权重衰减，是在梯度下降更新参数的时候，将上一次的参数，乘上一个衰减项（1-β）

权重衰减(Weight Decay)是一种有效的正则化方法，在每次参数更新时引入一个衰减系数。
$$
\theta_t \leftarrow (1 - \beta)\theta_{t-1} - \alpha \mathbf g_t,
$$
其中$\mathbf g_t$为第$t$步更新时的梯度，$\alpha$为学习率，$\beta$为权重衰减系数，一般取值比较小，比如0.0005。

完善BatchGD优化器，增加权重衰减系数。定义gradient_descent函数，在参数更新时增加衰减系数。代码实现如下：

alec：

  • 参数更新的时候，乘上衰减权重系数weight_decay为什么能够正则化？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class BatchGD(Optimizer):
    def __init__(self, init_lr, model, weight_decay):
        """
        小批量梯度下降优化器初始化
        输入：
            - init_lr: 初始学习率
            - model：模型，model.params字典存储模型参数值
        """
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)
        self.weight_decay = weight_decay

    # 梯度下降更新参数的方法
    def gradient_descent(self, x, gradient_x, init_lr):
        """
        梯度下降更新一次参数
        """
        x = (1 - self.weight_decay) * x - init_lr * gradient_x
        return x

    # 遍历各个参数，更新
    def step(self):
        """
        参数更新
        输入：
            - gradient：梯度字典，存储每个参数的梯度
        """
        for layer in self.model.layers:
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = self.gradient_descent(layer.params[key], layer.grads[key], self.init_lr)
1
2
运行时长: 5毫秒
结束时间: 2022-12-25 21:31:36

设置权重衰减系数为0.001。代码实现如下：

1
2
3
4
5
paddle.seed(0)
model = MLP_3L(layers_size)
opt = BatchGD(init_lr=0.2, model=model, weight_decay=0.001) # 优化器是用来更新参数的，所以权重衰减这个动作是放在优化器中的
loss_fn = BinaryCrossEntropyWithLogits(model, lambd=0)
losses = train_model(X_train, y_train, X_test, y_test, model, opt, loss_fn, num_iters=50000)

从输出结果看，训练集上的准确率为84.5%，测试集上的准确率为75%，猜测仍存在过拟合现象，但是现象得到缓解。

下面通过可视化分类界面证猜测试结果。代码实现如下：

1
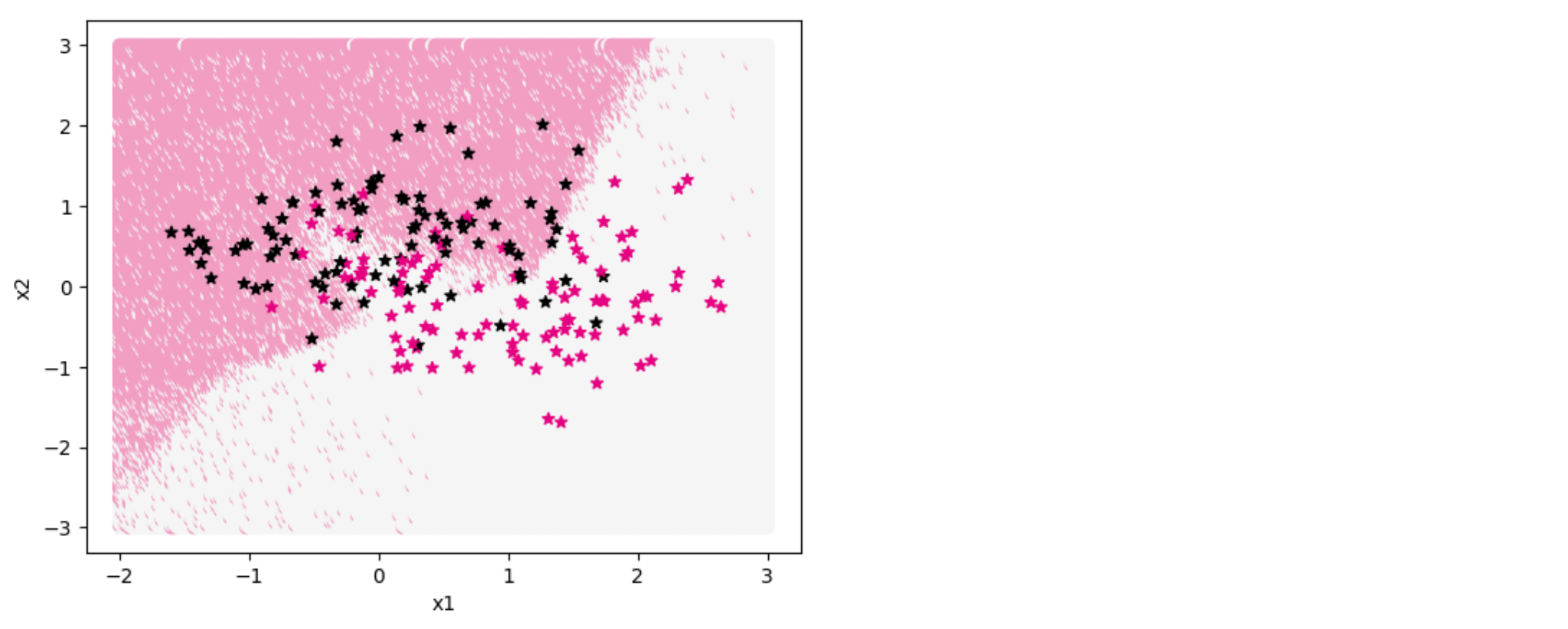
show_class_boundary(model, X_train, y_train, fig_name='opti-regularization3.pdf')

从输出结果看，权重衰减也可以有效缓解过拟合现象

image-20221225230646822

[√] 7.6.5 暂退法

alec：

  • 当训练一个深度神经网络时，我们可以随机暂退一部分神经元（即置为0）来避免过拟合，这种方法称为暂退法(Dropout Method)。

  • 每次选择暂退的神经元是随机的，最简单的方法是设置一个固定的概率$p$，对每一个神经元都以概率$p$来判定要不要保留。

  • 假设一批样本的某个神经层为$X\in \mathbb{R}^{B\times D}$，其中$B$为批大小，$D$为该层神经元数量，引入一个掩码矩阵$ M \in \mathbb{R}^{B\times D}$，每个元素的值以$p$的概率置为0，$1-p$的概率置为1。

  • 由于掩蔽某些神经元后，该神经层的活性值的分布会发生变化。

  • 而在测试阶段时不使用暂退，这会使得训练和测试两个阶段该层神经元的活性值的分布不一致，并对之后的神经层产生影响，发生协变量偏移现象。（协变量偏移现象）

  • 因此，为了在使用暂退法时不改变活性值$ X$的方差，将暂退后保留的神经元活性值放大原来的$1/(1-p)$倍。这样可以保证下一个神经层的输入在训练和测试阶段的方差基本一致。（解决协变量偏移现象：将留存下来的激活值放大）

  • 暂退函数$\mathrm{dropout}$定义为
    $$
    \tilde{ X}=\mathrm{dropout}( X) \triangleq
    \begin{cases}
    ( X \odot M)/(1-p) & \text{当训练阶段时}, \
    X & \text{当测试阶段时}.
    \end{cases}
    $$

  • 暂退法，先将一部分神经元的活性值以概率P留存，然后再将留存的数据方法，以以免协变量偏移现象

提醒

和《神经网络与深度学习》中公式(7.74)不同。两者都可以解决使用暂退法带来的协变量偏移问题，但本书的方法在实践中更常见。

在反向计算梯度时，令$\delta_{\tilde{ X}}=\frac{\partial \mathcal L}{\partial \tilde{ X}}$，
则有
$$
\delta_{ X} = \delta_{\tilde{ X}} \odot M /(1-p).
$$

这里可以看出，暂退神经元的梯度也为$0$。

[√] 7.6.5.1 Dropout算子

定义Dropout算子，实现前向和反向的计算。注意，Dropout需要区分训练和评价模型。代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Dropout(Op):
    def __init__(self, drop_rate):
        self.mask = None
        self.drop_rate = drop_rate

    def forward(self, inputs):
        # 生成一个丢弃掩码
        mask = paddle.cast(paddle.rand(inputs.shape) > self.drop_rate, dtype='float32')
        self.mask = mask
        # 随机使一些神经元失效
        inputs = paddle.multiply(inputs, mask)
        # 使输入的方差保持不变
        inputs /= (1 - self.drop_rate)
        return inputs

    def backward(self, outputs_grad):
        return paddle.multiply(outputs_grad, self.mask) / (1 - self.drop_rate)
1
2
运行时长: 5毫秒
结束时间: 2022-12-25 22:07:08

定义MLP_3L_dropout模型，，实现带暂退法的网络前反向计算。代码实现如下：

alec：

  • dropout是用在激活值上，所以经过激活之后，再使用dropout
  • BN则是先经过线性函数，然后BN，然后再送到激活函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from nndl.op import MLP_3L

class MLP_3L_dropout(MLP_3L):
    def __init__(self, layers_size, drop_rate):
        super(MLP_3L_dropout, self).__init__(layers_size)
        self.dropout1 = Dropout(drop_rate)
        self.dropout2 = Dropout(drop_rate)
        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2, self.fc3]

    def __call__(self, X, mode='train'):
        return self.forward(X, mode)

    def forward(self, X, mode='train'):
        # 全连接、激活、dropout、全连接、激活、dropout、全连接
        self.mode = mode
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        if self.mode == 'train':
            a1 = self.dropout1(a1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        if self.mode == 'train':
            a2 = self.dropout2(a2)
        z3 = self.fc3(a2)
        return z3

    def backward(self, loss_grad_z3):
        loss_grad_a2 = self.fc3.backward(loss_grad_z3)
        if self.mode == 'train':
            loss_grad_a2 = self.dropout2.backward(loss_grad_a2)
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        if self.mode == 'train':
            loss_grad_a1 = self.dropout1.backward(loss_grad_a1)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

设置丢弃概率为0.5。代码实现如下：

1
2
3
4
5
paddle.seed(0)
model = MLP_3L_dropout(layers_size, drop_rate=0.3)
opt = BatchGD(init_lr=0.2, model=model, weight_decay=0)
loss_fn = BinaryCrossEntropyWithLogits(model, lambd=0)
losses = train_model(X_train, y_train, X_test, y_test, model, opt, loss_fn, 50000, 'dev')

alec：

  • L2正则化，是对损失添加L2正则项
  • 权重衰减，是在梯度下降参数更新的时候，对旧的参数做衰减
  • dropout，是对神经元做随机的丢弃
1
2
train accuracy: [0.8549999]
test accuracy: [0.76]

从输出结果看，训练集上的准确率为85.5%，测试集上的准确率为76%，猜测仍存在过拟合现象，但是现象得到缓解。

通过可视化分类界面证实猜想结果。代码实现如下：

1
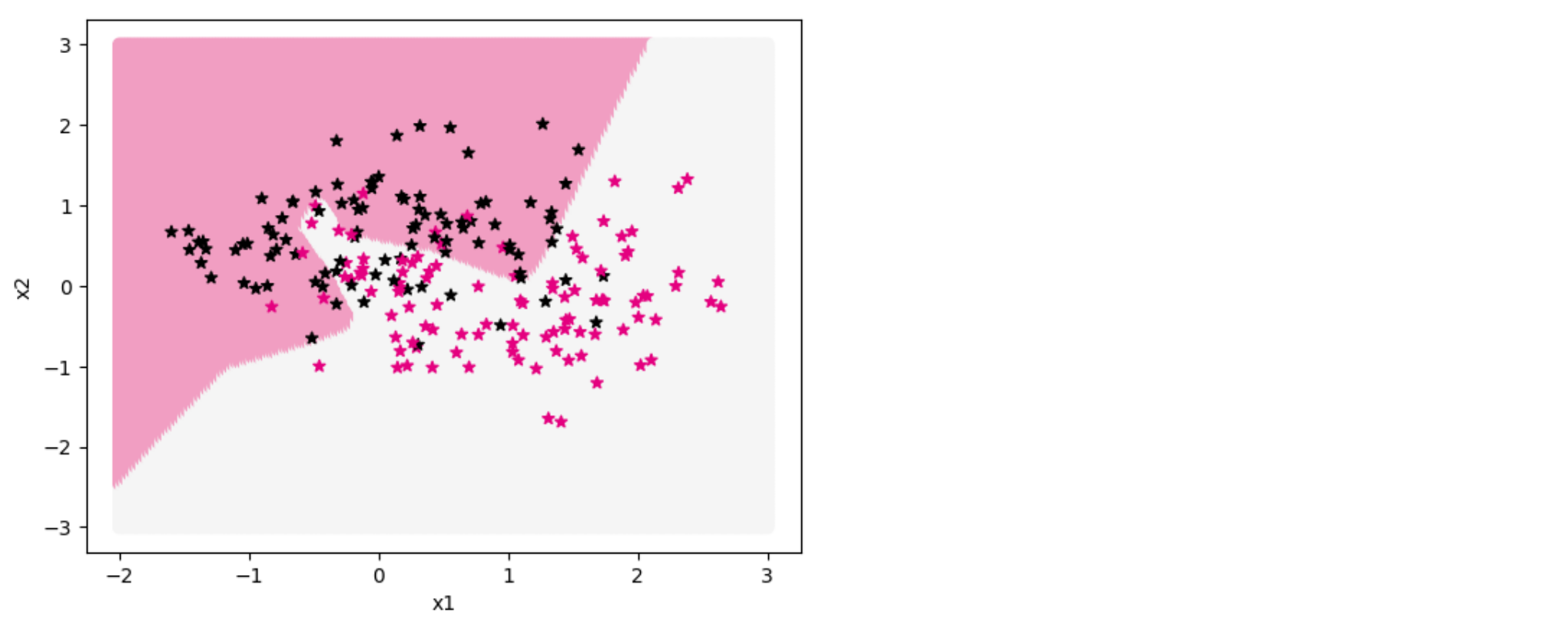
show_class_boundary(model, X_train, y_train, 'dev', fig_name='opti-regularization4.pdf')

从输出结果看，暂退法可以有效缓解过拟合，但缓解效果不如正则化或权重衰减明显。

alec：

  • 从结果来看，暂退法可以有效的缓解过拟合，但是缓解效果不如正则化或权重衰减明显

image-20221225230606475

[√] 7.7 小结

本章通过动手实现不同的优化器和正则化方法来加深对神经网络优化和正则化的理解。

在网络优化方面，首先从影响神经网络优化的三个主要因素（批大小、学习率、梯度计算）进行实验比较来看它们对神经网络优化的影响。为了更好地可视化，我们还进行2D和3D的优化过程展示。除了上面的三个因素外，我们还动手实现了基于随机采样的参数初始化方法以及逐层规范化方法来进一步提高网络的优化效率。

在网络正则化方面，我们动手实现了ℓ2正则化、权重衰减以及暂退法，并展示了它们在缓解过拟合方面的效果。

[√] 参考文献

[√] 附录

深度学习技术栈 > 深度学习 > 实践学习 > 神经网络与深度学习：案例与实践 - 飞桨 - 邱锡鹏
7 - 网络优化与正则化 - 书籍3
https://alec-97.github.io/posts/3720136123/
作者
Shuai Zhao
发布于
2022年12月25日
许可协议