040 - 文章阅读笔记：ACNet|增强局部显著特征，哈工大左旺孟老师团队提出非对称卷积用于图像超分 - AIWalker

本文最后更新于：3 个月前

原文链接：ACNet|增强局部显著特征，哈工大左旺孟老师团队提出非对称卷积用于图像超分 - AIWalker

2021-04-04 21:30

[√] 文章信息

标题&作者团队

Code:https://github.com/hellloxiaotian/ACNet

本文是哈工大左旺孟老师团队在图像超分方面的最新工作，已被IEEE TSMC收录。本文将ACNet中的非对称卷积思想与LESRCNN进行组合，取得了更好的性能。由于作者尚未开源，故笔者进行了简单的复现，复现还是挺容易的，哈哈。

[√] 摘要

本文提出了一种非对称CNN网络ACNet，它由非对称模块(AB)、记忆力增强模块(MEB)、高频特征增强模块(HFFEB)构成。其中非对称模块采用两个一维卷积从水平和垂直方向对方框卷积进行增强，提升局部显著特征的影响性因子；MEB则通过残差链接方式对AB提取的低频特征进行融合，将低频特征变换到高频特征；HFFEB则融合低频与高频特征得到更鲁棒性的超分特征。实验结果表明：本文所提ACNet可以有效解决SISR、盲SISR以及噪声不可知盲SISR等问题。

本文主要贡献包含以下几点：

提出一种多级特征融合机制，通过对低频特征和高频特征融合，它可以很好的解决长期依赖问题，避免了上采样机制导致性能退化问题。
提出一种非对称架构增强局部关键点的影响性以得到了鲁邦的低频特征；
提出一种灵活的上采样机制，它可以使得所提方案解决SISR等问题。

[√] 方法

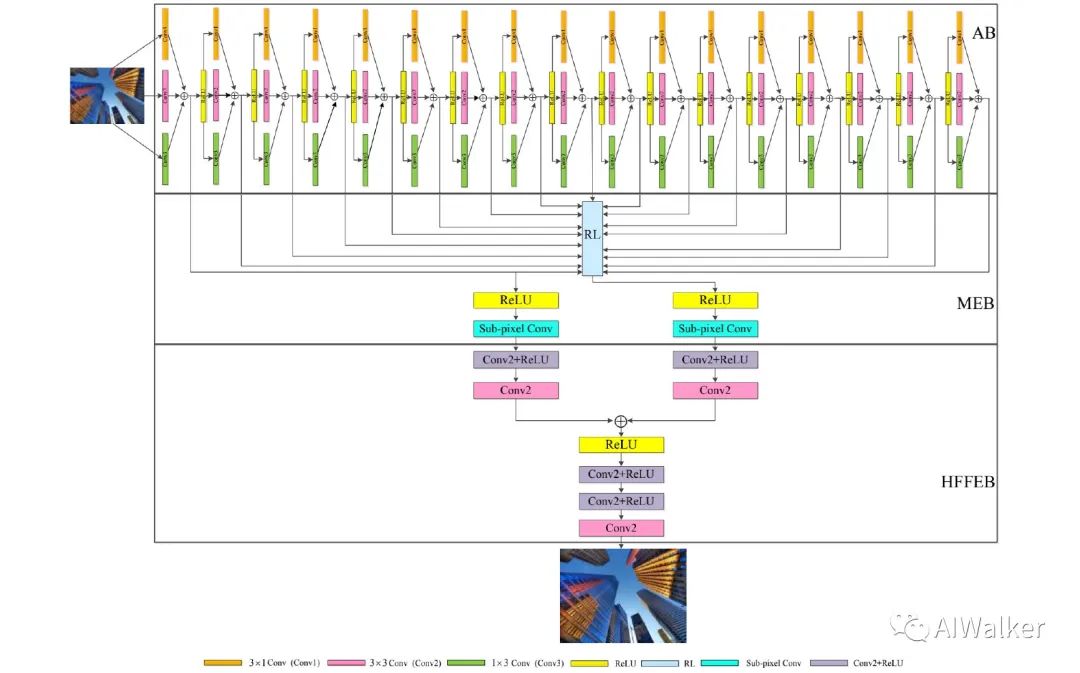
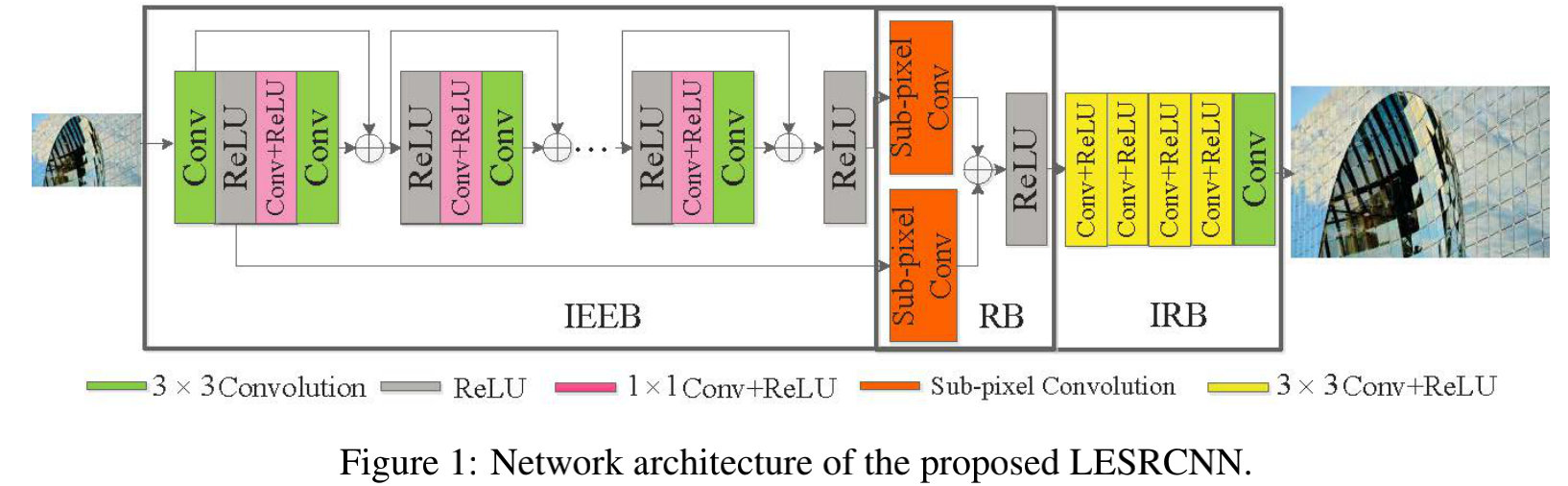
上图给出了本文所提非对称卷积网络ACNet结构示意图，它由三个模块构成：深度为17的AB模块、深度为1的MEB以及深度为5的HFFEB。

AB部分与2019年丁霄汉博士提出的ACNet中的ACB模块基本一致：训练时三个分支：一个分支为1x3卷积，一个分支为3x1，一个分支为3x3卷积；推理时三个分支可以合并为单一卷积。
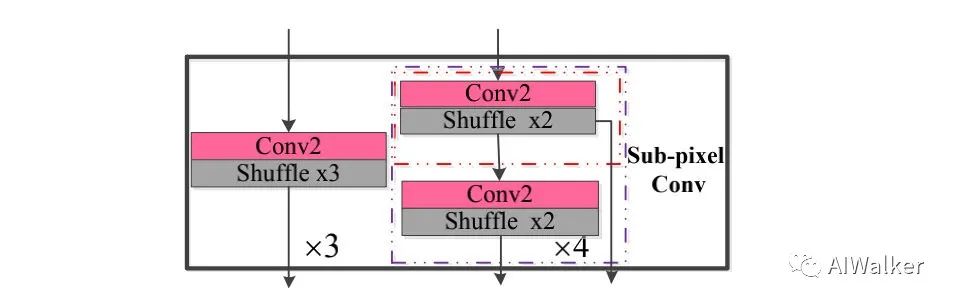
MEB则是对所有AB提取的特征通过残差学习方式进行融合，并将所提取的低频特征转换为高频特征。注：该模块同时还进行了特征上采样。其中sub-conv部分的结构示意图如下所示。这里与EDSR中的上采样基本一样，略过咯。

alec：

ACB，非对称模块，训练时三个分支：一个分支为1x3卷积，一个分支为3x1，一个分支为3x3卷积；推理时三个分支可以合并为单一卷积。

HFFEB则对源自LR的低频特征以及上述融合高频特征进行融合处理得到更精确的超分特征。这个地方是本文所提方法与之前常见网络不同之处：在更高分辨率采用更多卷积进行增强以提升重建性能。
损失函数方面，本文选择了MSE损失.

本文所设计的网络实在过于简单，好像并没有什么需要深入介绍，看图就够了，或者看文末的参考实现亦可。

alec：

MEB部分将特征进行融合，HFFFB部分则将低频信息和融合之后的高频信息进行融合得到更精确的超分信息。

[√] 实验

在训练方面，作者采用两步法：(1) DIV2K的训练集+验证集同时参与训练；(2) DIV2K的训练集上进行微调。

直接上结果，下面两个图给出了Set5、Set14、B100、U100等数据的性能对比。

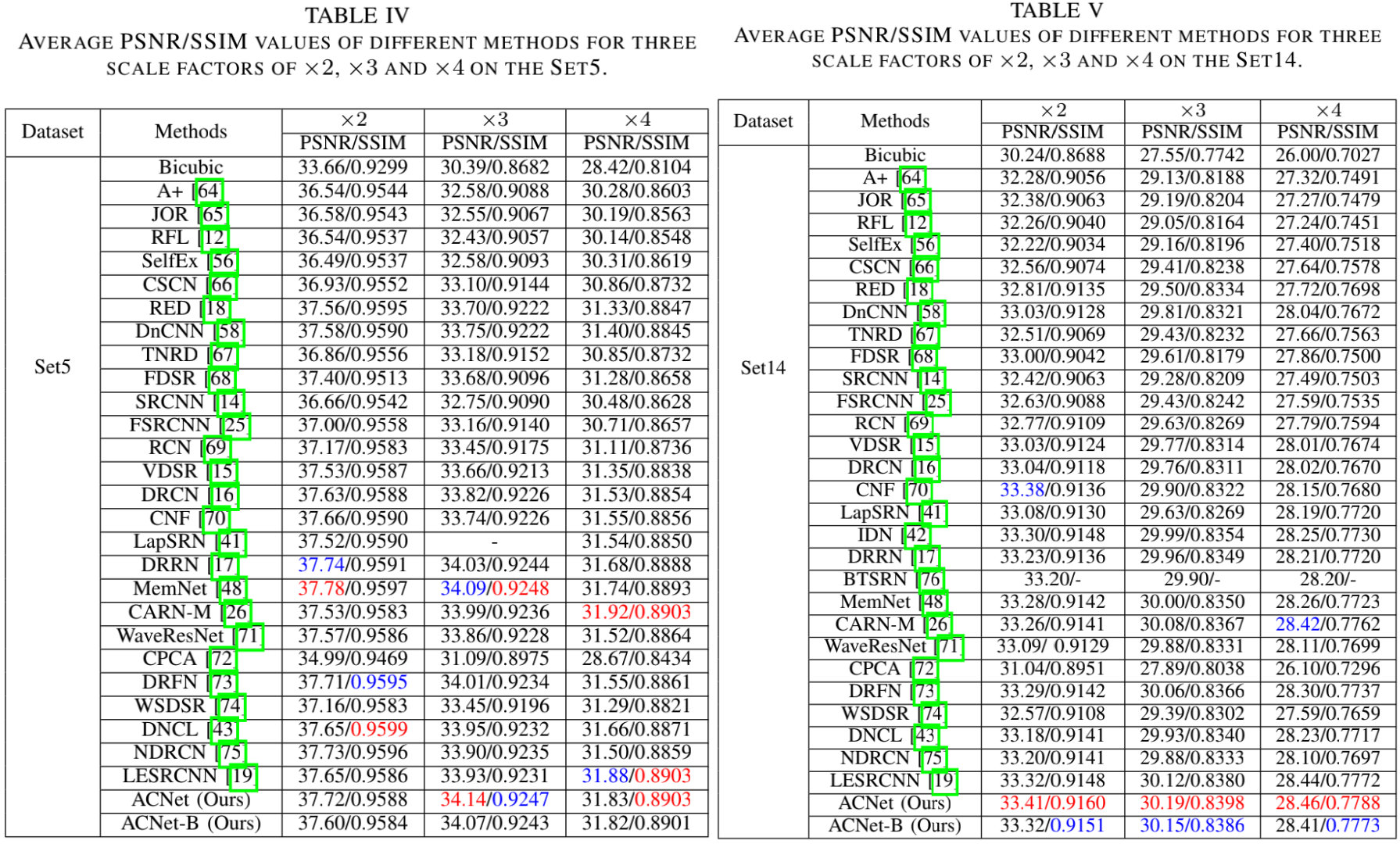
Set5&Set14

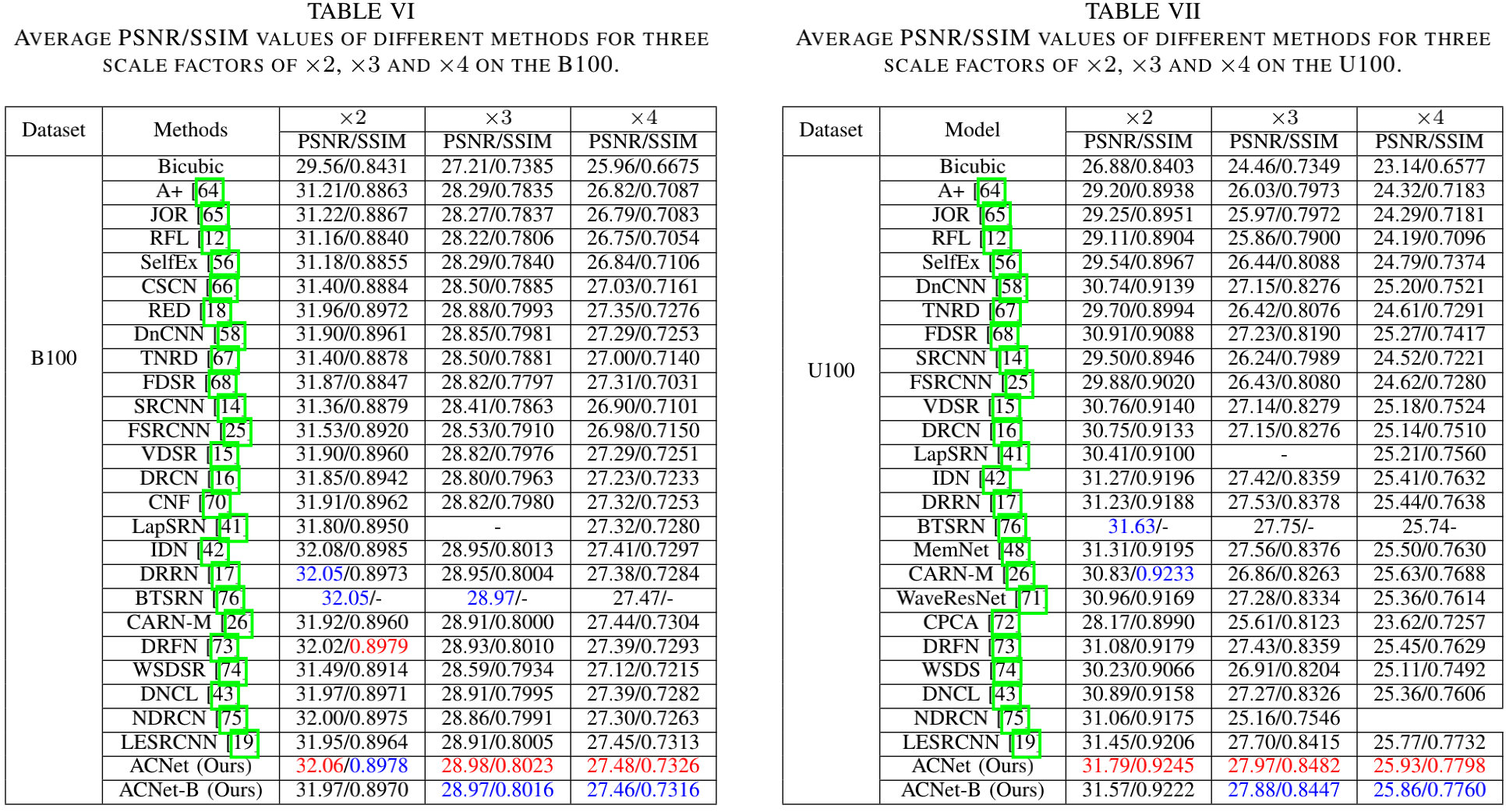
从上面四个表可以看到：在三个尺度上，本文所提ACNet均取得了还不错的性能。

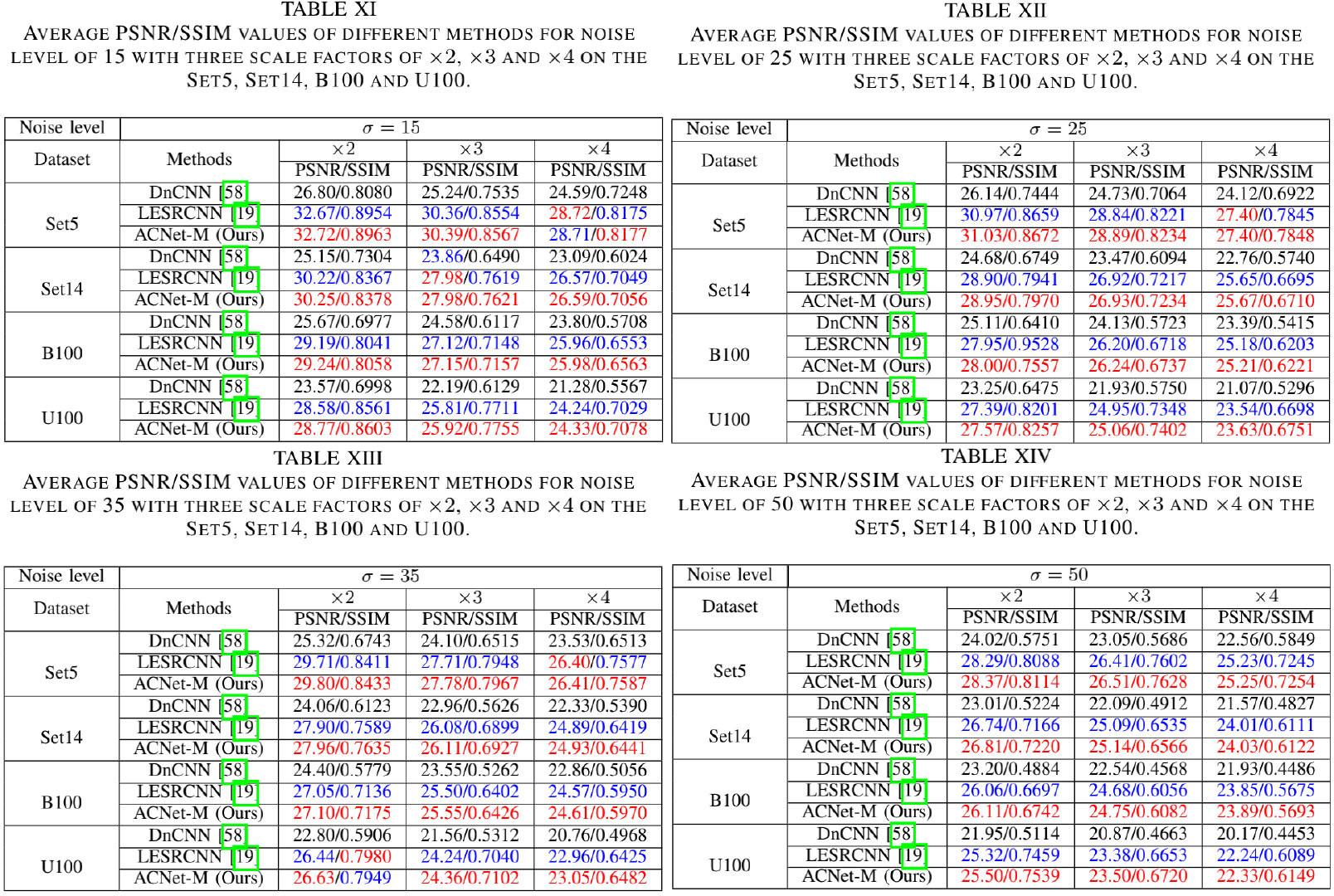
上表给出了不同噪声强度下的图像超分性能对比。在计算复杂度、推理耗时、性能以及视觉效果方面，所提方法ACNet取得了比较好的均衡。

[√] 题外语

lesrcnn

这篇论文整体看上去非常简洁，思想也比较简单。在网络结构方面，它与LESRCNN的结构上基本是一致的；而LESRNN与EDSR也是非常的相似。区别有这么三点：

重建部分：EDSR在上采样最终的分辨率后直接采用一个卷积进行重建；而LESRCNN在上采样到最终分辨率后采用了5层卷积进行处理。LESRCNN的这种处理方法无疑会造成比较大的计算量。
残差模块部分：EDSR中的残差模块采用Conv-ReLU-Conv方式；而LESRCNN则采用ReLU-Conv-ReLU-Conv方式。
低频特征与高频特征融合部分：EDSR中用于融合的特征并未经ReLU处理，先add再上采样；而LESRCNN则用ReLU进行了处理，然而分别用sub-conv上采样后再融合。

alec：

LESRCNN中的低频信息部分，先是通过relu进行了处理，然后再上采样，然后再相加。而EDSR中则是直接相加，然后再上采样。

再回过来头看LESRCNN与ACNet，则基本属于将2019年提出的ACNet在LESCNN中的直接应用；事实上，ACNet与IMDN的组合的可行性在2020年的超分竞赛中已得到了印证。所以，这篇文章的创新之处着实不多。

另外，需要吐槽的一点：这里对比的都是一些比较早期的方法，像最近两年的IMDN、RFANet、RFDN、PAN等优秀的轻量型模型均未进行对比。

不过这篇论文有一点值得称赞：复现难度非常低。笔者粗看了下结构花了很少时间就完成了code的实现，并仅仅基于DIV2K训练数据训练了66W步。在BI退化方面，笔者训练的模型性能要比作者文中列出来的指标高0.04-0.1dB不等。ACNet的参考实现code如下所示。

[√] 参考代码

class MeanShift(nn.Conv2d):
    def __init__(self,
                 rgb_range=1.0,
                 rgb_mean=(0.4488, 0.4371, 0.4040),
                 rgb_std=(1.0, 1.0, 1.0),
                 sign=-1):
        super(MeanShift, self).__init__(3, 3, kernel_size=1)
        std = torch.Tensor(rgb_std)
        self.weight.data = torch.eye(3).view(3, 3, 1, 1) / std.view(3, 1, 1, 1)
        self.bias.data = sign * rgb_range * torch.Tensor(rgb_mean) / std
        self.requires_grad = False

        
class Upsampler(nn.Sequential):
    def __init__(self,
                 scale,
                 channels,
                 bn=False,
                 act=False,
                 bias=True):
        m = []
        if (scale & (scale - 1)) == 0:
            for _ in range(int(math.log(scale, 2))):
                m.append(nn.Conv2d(channels, 4 * channels, 3, 1, 1, bias=bias))
                m.append(nn.PixelShuffle(2))
                if bn:
                    m.append(nn.BatchNorm2d(channels))
                if act:
                    m.append(nn.ReLU(inplace=True))
        elif scale == 3:
            m.append(nn.Conv2d(channels, 9 * channels, 3, 1, 1, bias=bias))
            m.append(nn.PixelShuffle(3))
            if bn:
                m.append(nn.BatchNorm2d(channels))

            if act:
                m.append(nn.ReLU(inplace=True))
        else:
            raise NotImplementedError
        super().__init__(*m)
        
        
class ACBlock(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(ACBlock, self).__init__()
        self.conv1x3 = nn.Conv2d(in_channels, out_channels, (1, 3), 1, (0, 1))
        self.conv3x1 = nn.Conv2d(in_channels, out_channels, (3, 1), 1, (1, 0))
        self.conv3x3 = nn.Conv2d(in_channels, out_channels, (3, 3), 1, (1, 1))

    def forward(self, x):
        conv3x1 = self.conv3x1(x)
        conv1x3 = self.conv1x3(x)
        conv3x3 = self.conv3x3(x)
        return conv3x1 + conv1x3 + conv3x3
      
      
class ACNet(nn.Module):
    def __init__(self,
                 scale=2,
                 in_channels=3,
                 out_channels=3,
                 num_features=64,
                 num_blocks=17,
                 rgb_range=1.0):
        super(ACNet, self).__init__()
        self.scale = scale
        self.num_blocks = num_blocks
        self.num_features = num_features

        # pre and post process
        self.sub_mean = MeanShift(rgb_range=rgb_range, sign=-1)
        self.add_mena = MeanShift(rgb_range=rgb_range, sign=1)

        # AB module
        self.blk1 = ACBlock(in_channels, num_features)
        for idx in range(1, num_blocks):
            self.__setattr__(f"blk{idx+1}", nn.Sequential(nn.ReLU(inplace=True), ACBlock(num_features, num_features)))

        # MEB
        self.lff = nn.Sequential(
            nn.ReLU(inplace=False),
            Upsampler(scale, num_features),
            nn.Conv2d(num_features, num_features, 3, 1, 1),
            nn.ReLU(inplace=True),
            nn.Conv2d(num_features, num_features, 3, 1, 1)
        )
        self.hff = nn.Sequential(
            nn.ReLU(inplace=False),
            Upsampler(scale, num_features),
            nn.Conv2d(num_features, num_features, 3, 1, 1),
            nn.ReLU(inplace=True),
            nn.Conv2d(num_features, num_features, 3, 1, 1)
        )

        # HFFEB
        self.fusion = nn.Sequential(
            nn.ReLU(inplace=False),
            nn.Conv2d(num_features, num_features, 3, 1, 1),
            nn.ReLU(inplace=True),
            nn.Conv2d(num_features, num_features, 3, 1, 1),
            nn.ReLU(inplace=True),
            nn.Conv2d(num_features, out_channels, 3, 1, 1),
        )

    def forward(self, x):
        inputs = self.sub_mean(x)
        blk1 = self.blk1(inputs)

        high = blk1
        tmp = blk1
        for idx in range(1, self.num_blocks):
            tmp = self.__getattr__(f"blk{idx+1}")(tmp)
            high = high + tmp

        lff = self.lff(blk1)
        hff = self.hff(high)

        fusion = self.fusion(lff + hff)
        output = self.add_mena(fusion)
        return output

深度学习技术栈 > 超分辨率重建 > 文章学习

#超分辨率重建

040 - 文章阅读笔记：ACNet|增强局部显著特征，哈工大左旺孟老师团队提出非对称卷积用于图像超分 - AIWalker

https://alec-97.github.io/posts/386882073/

作者

Shuai Zhao

发布于

2023年1月19日

许可协议

041 - 文章阅读笔记：VapSR | 手把手教你改进PAN，董超团队提出超大感受野注意力超分方案，已开源！ - 2022-10-24 08:00 - AIWalker 上一篇

039 - 文章阅读笔记：AIM2020-ESR 冠军方案解读：引入注意力模块 ESA，实现高效轻量的超分网络（附代码实现） - 极市平台 - ExtremeMart 下一篇