2 - 机器学习
本文最后更新于:3 个月前
2 - 课节2: 机器学习
2.0 - 机器学习概述

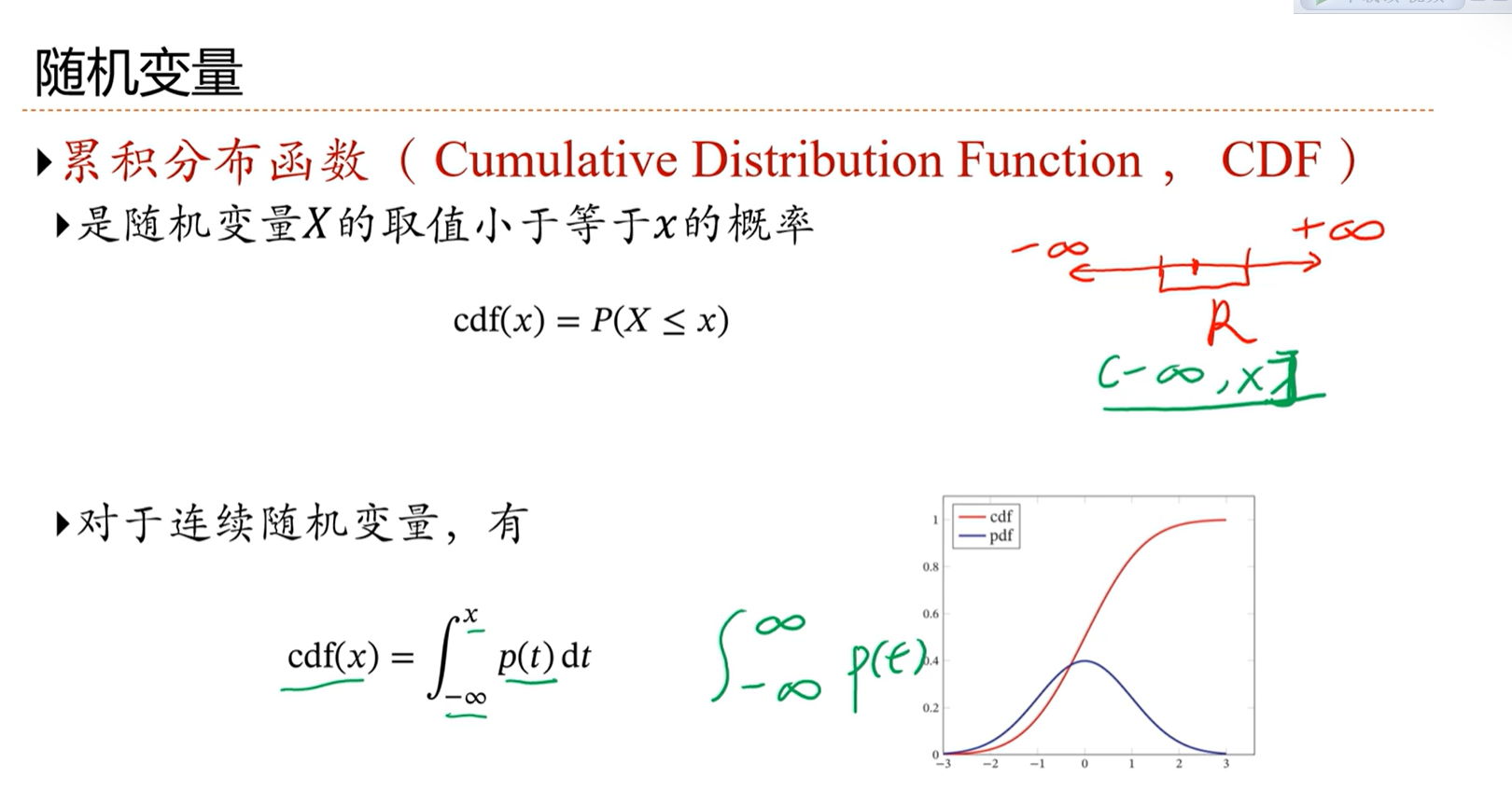
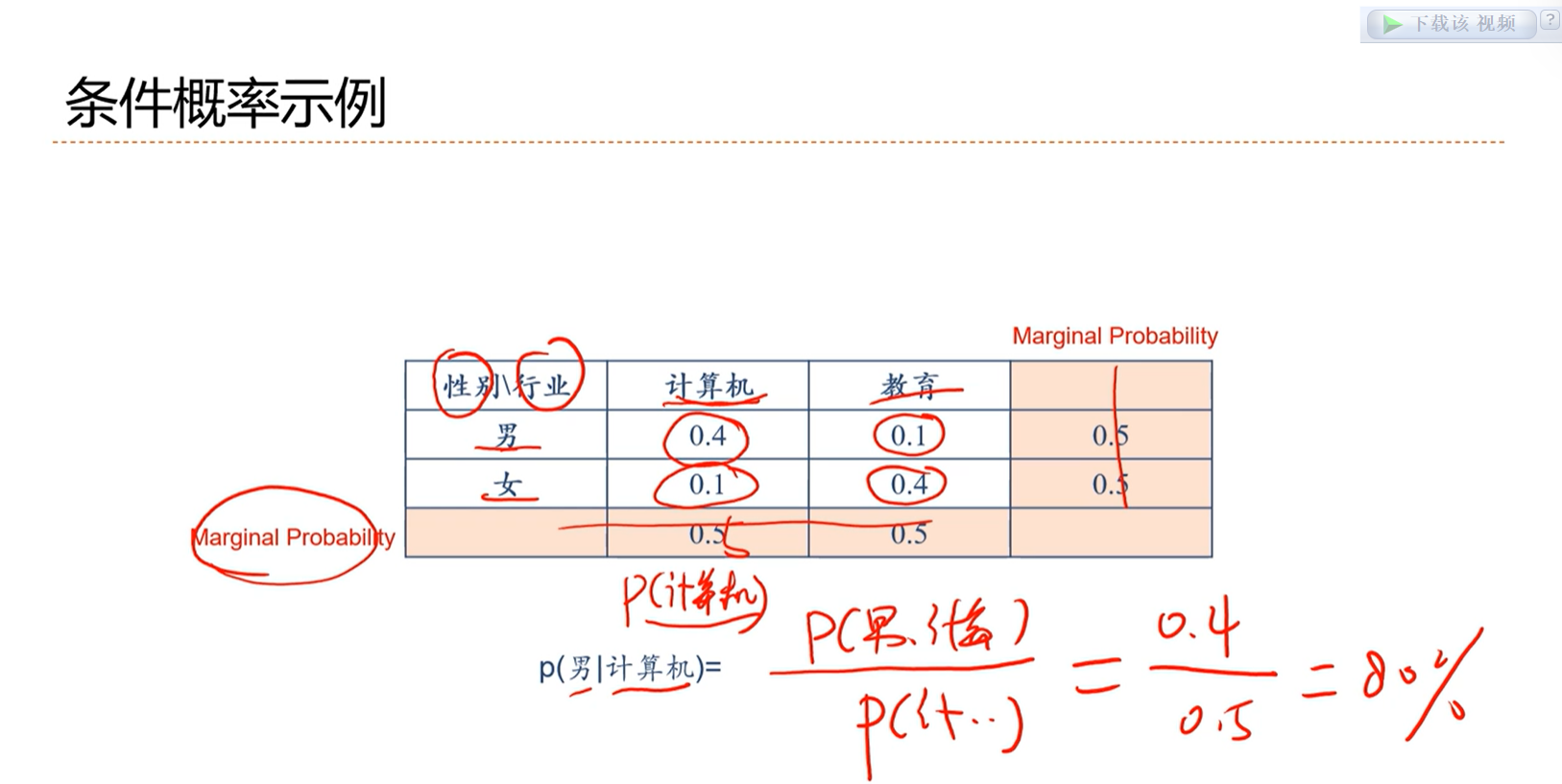
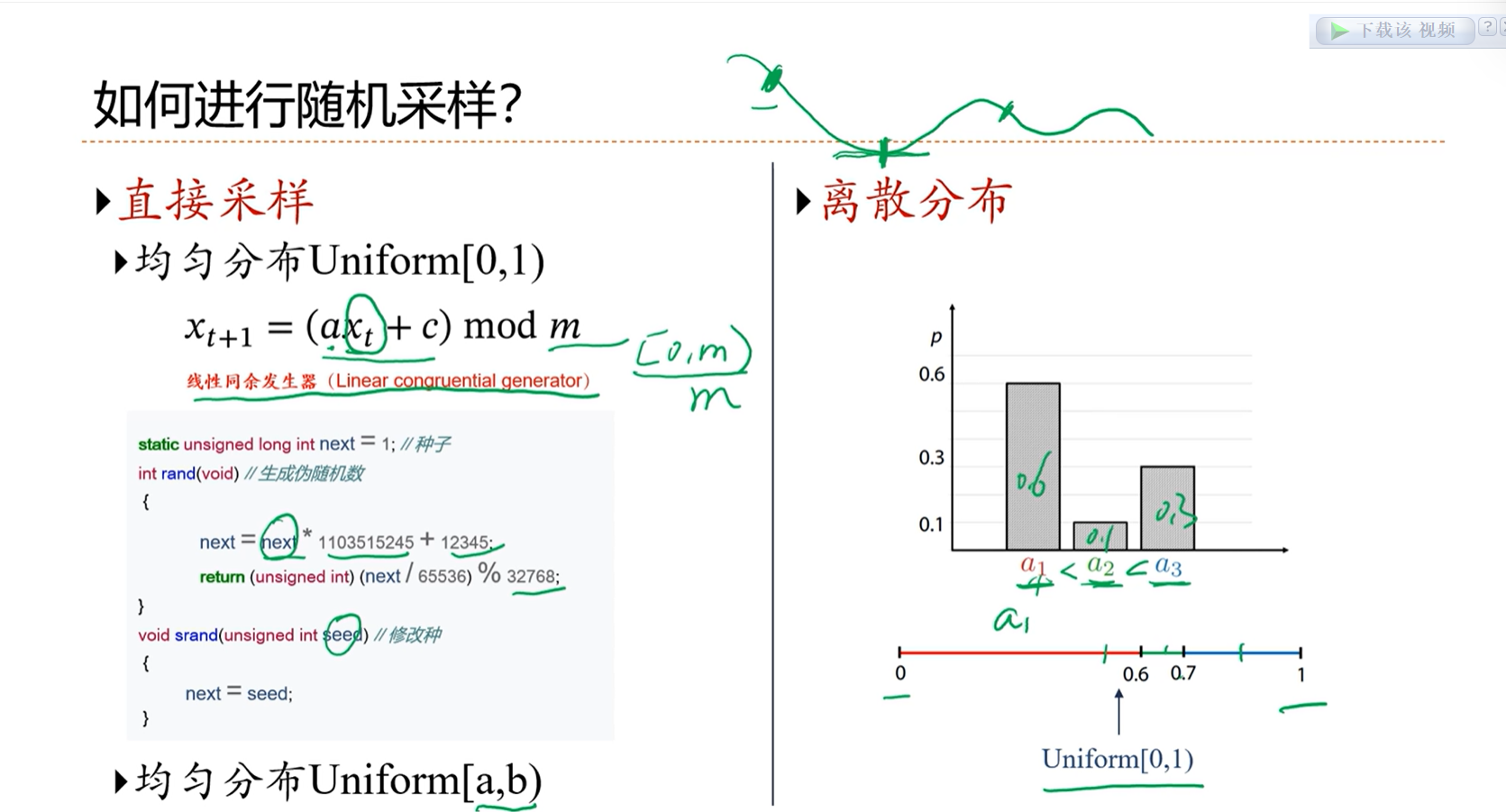
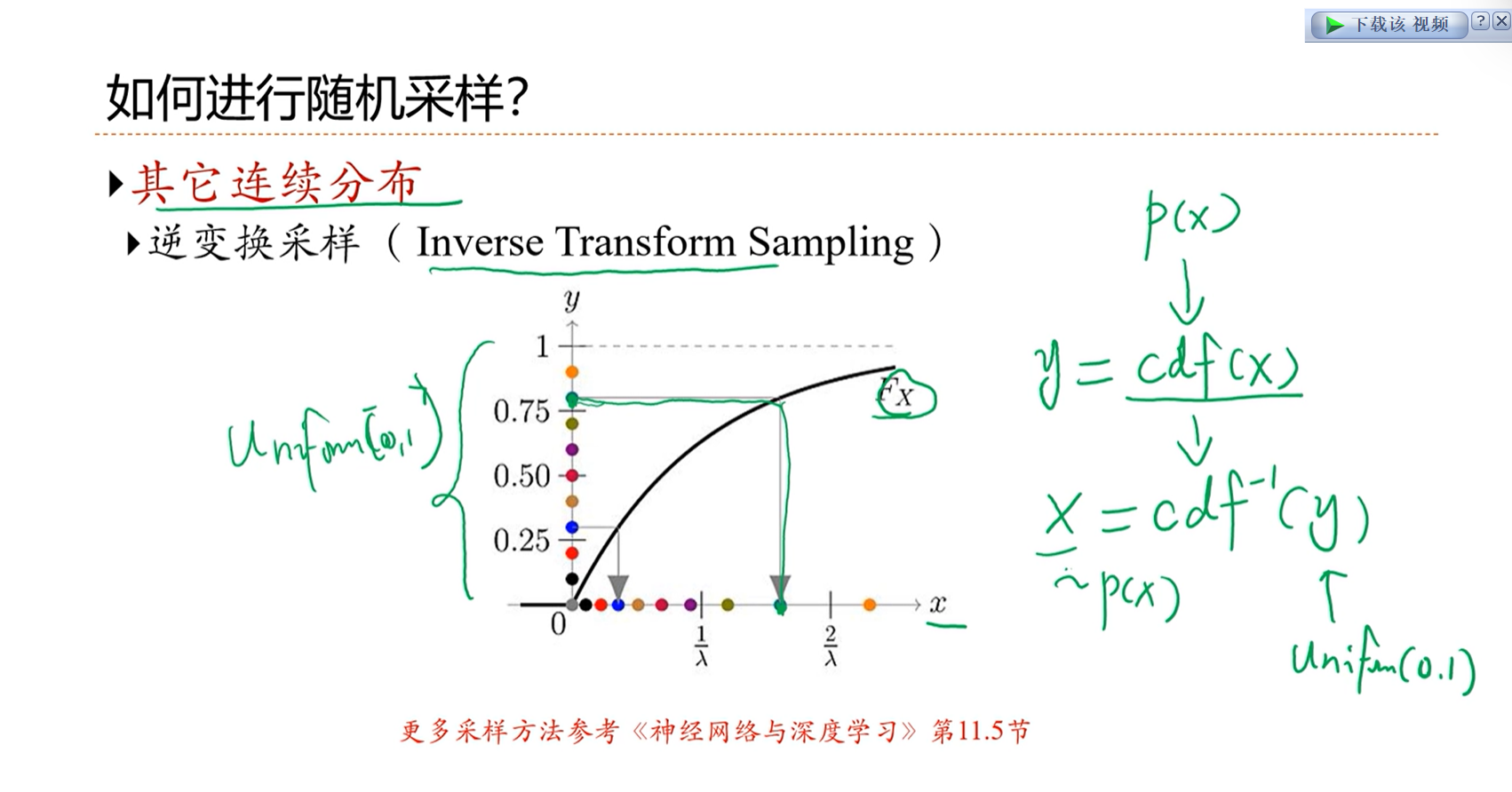
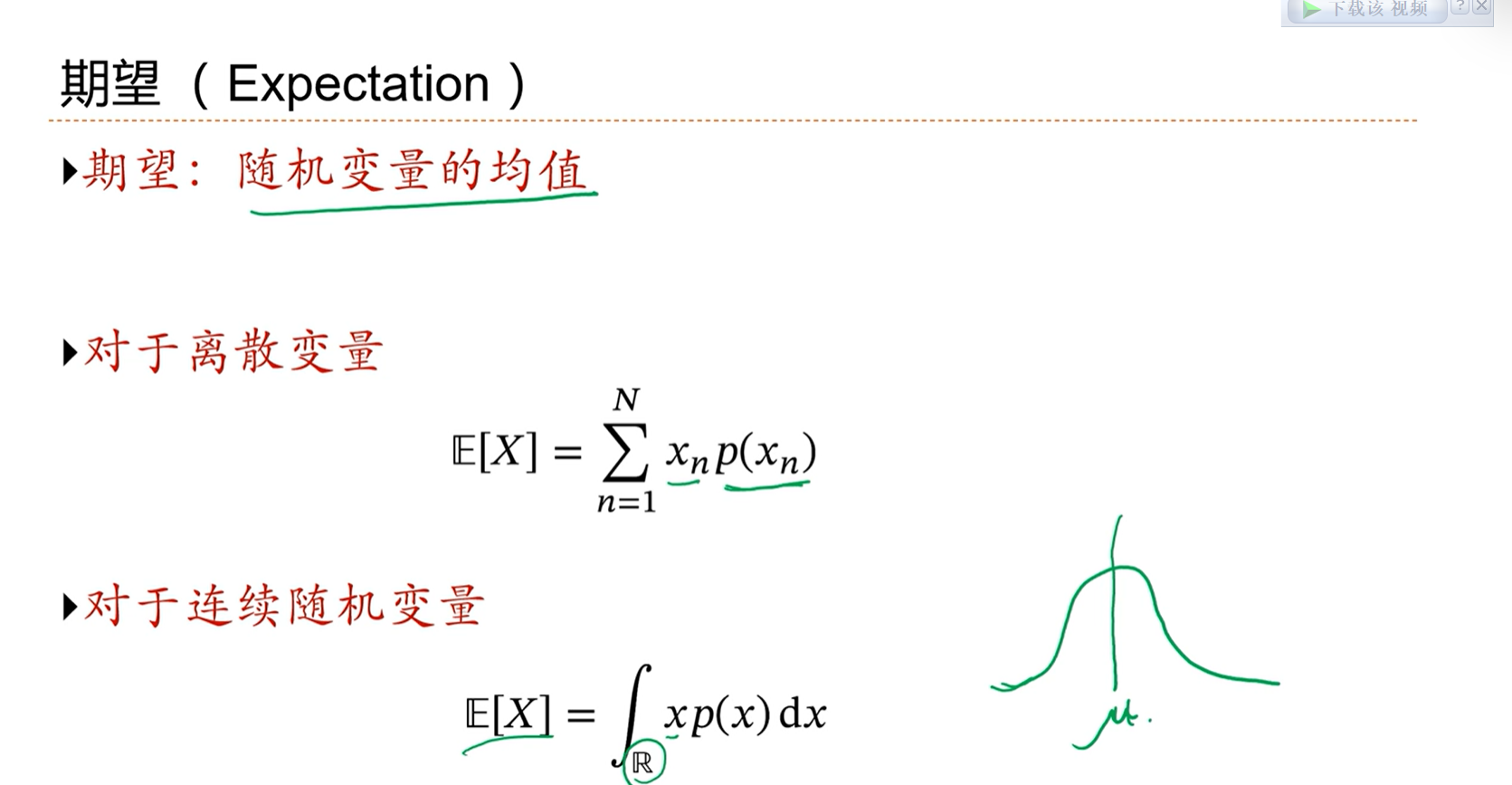
2.1 - 关于概率的一些基本概念







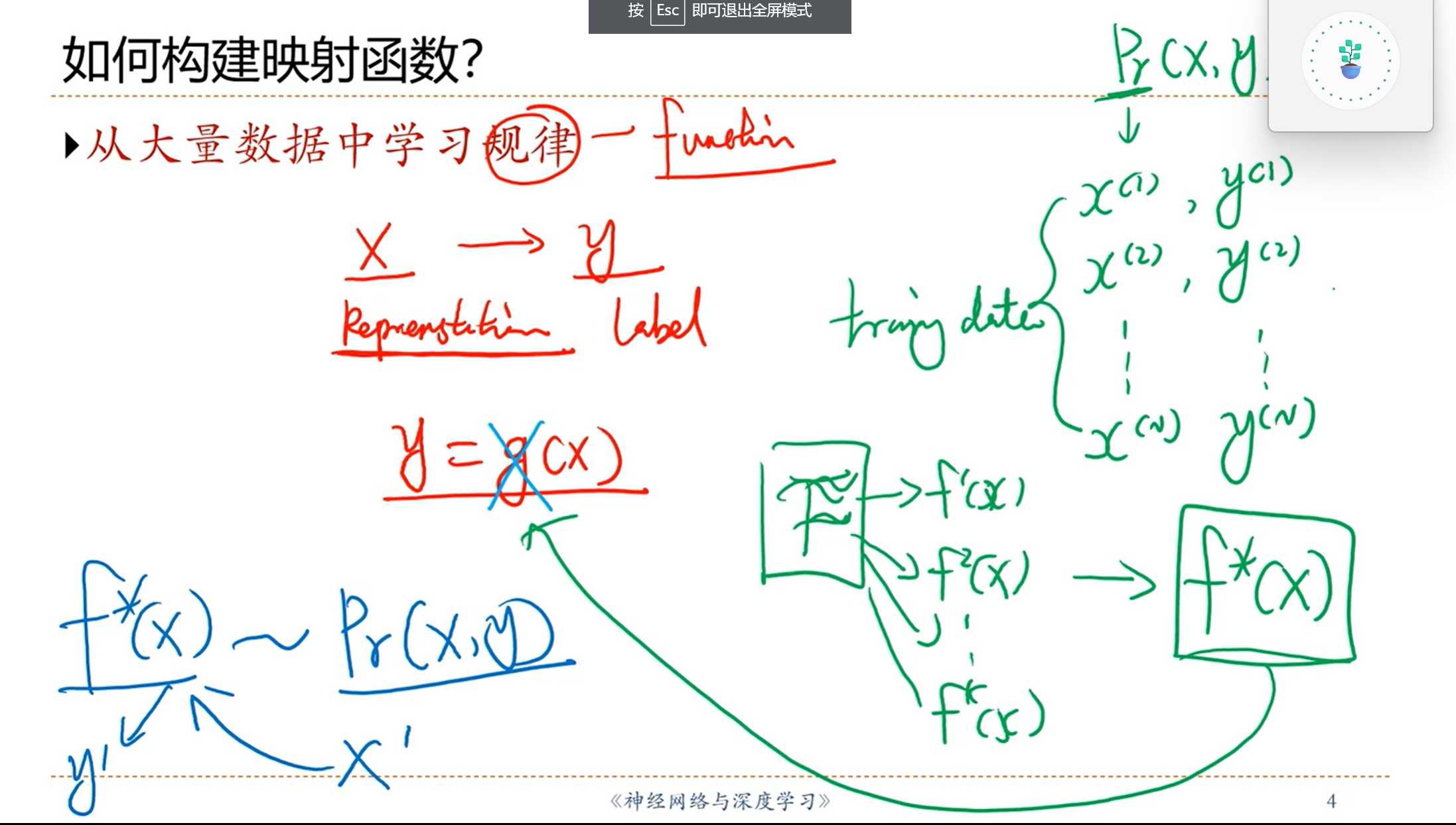
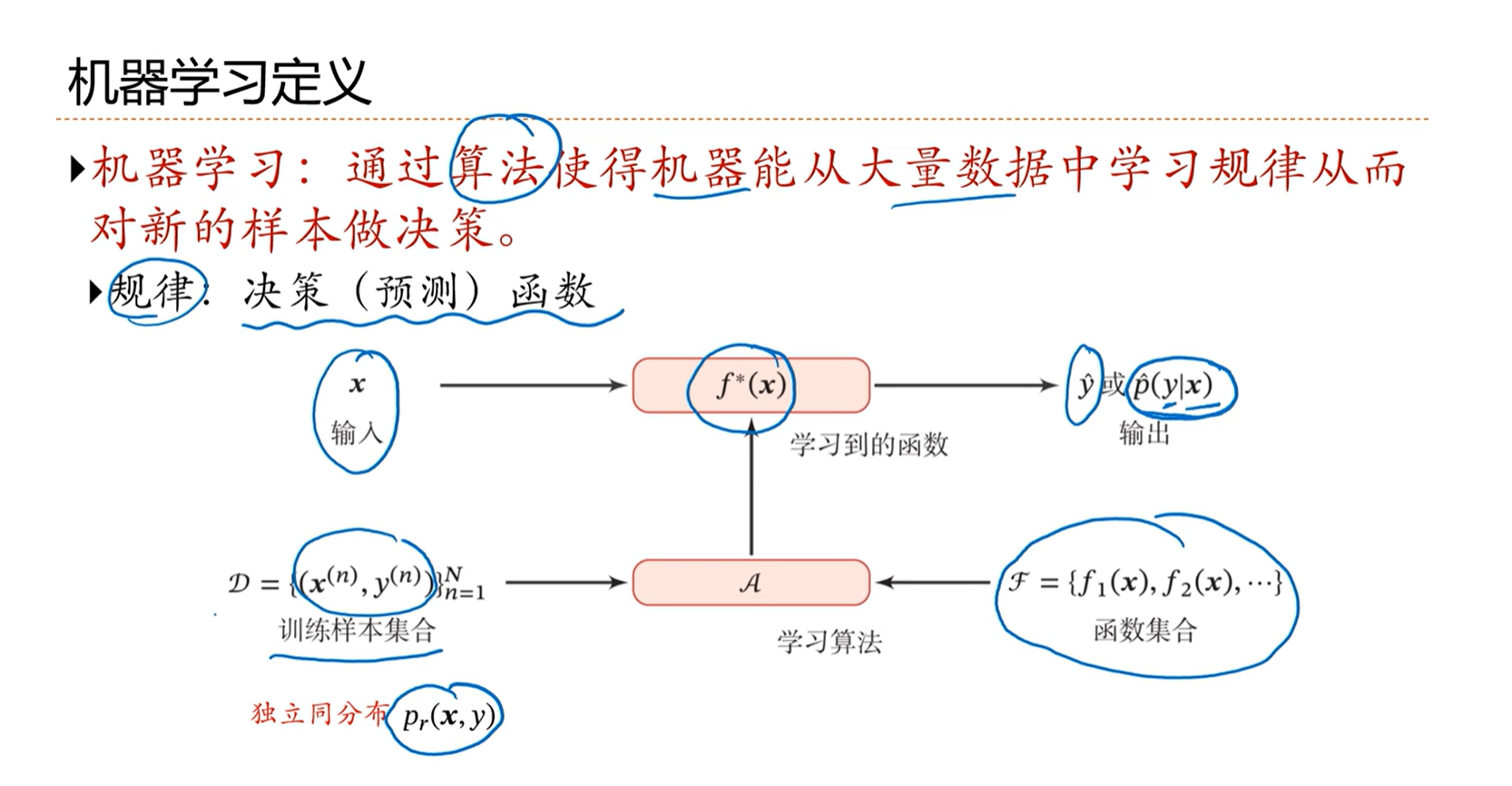
2.2 - 机器学习定义



2.3 - 机器学习类型
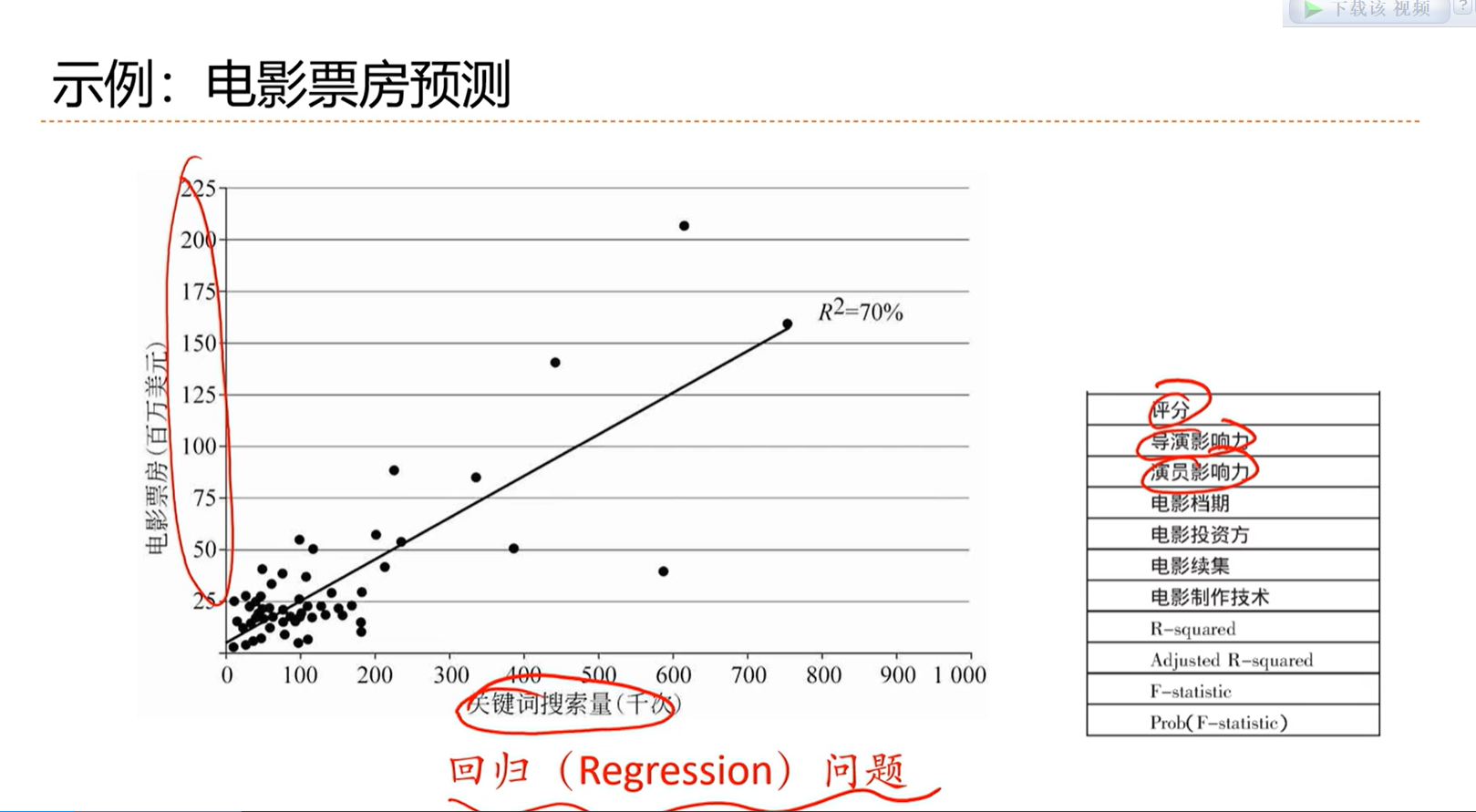
输出是连续的,这类问题称为回归问题。
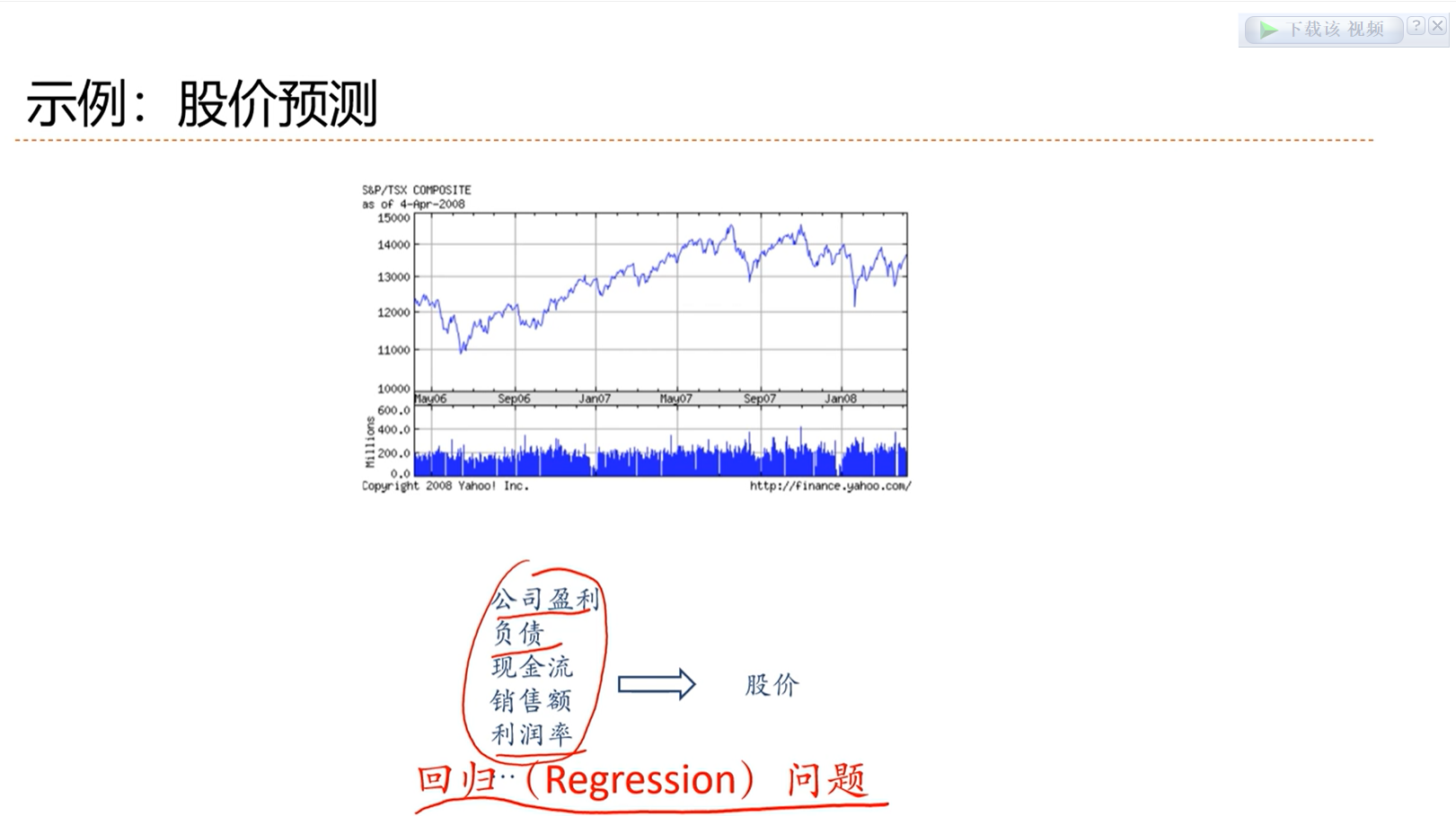
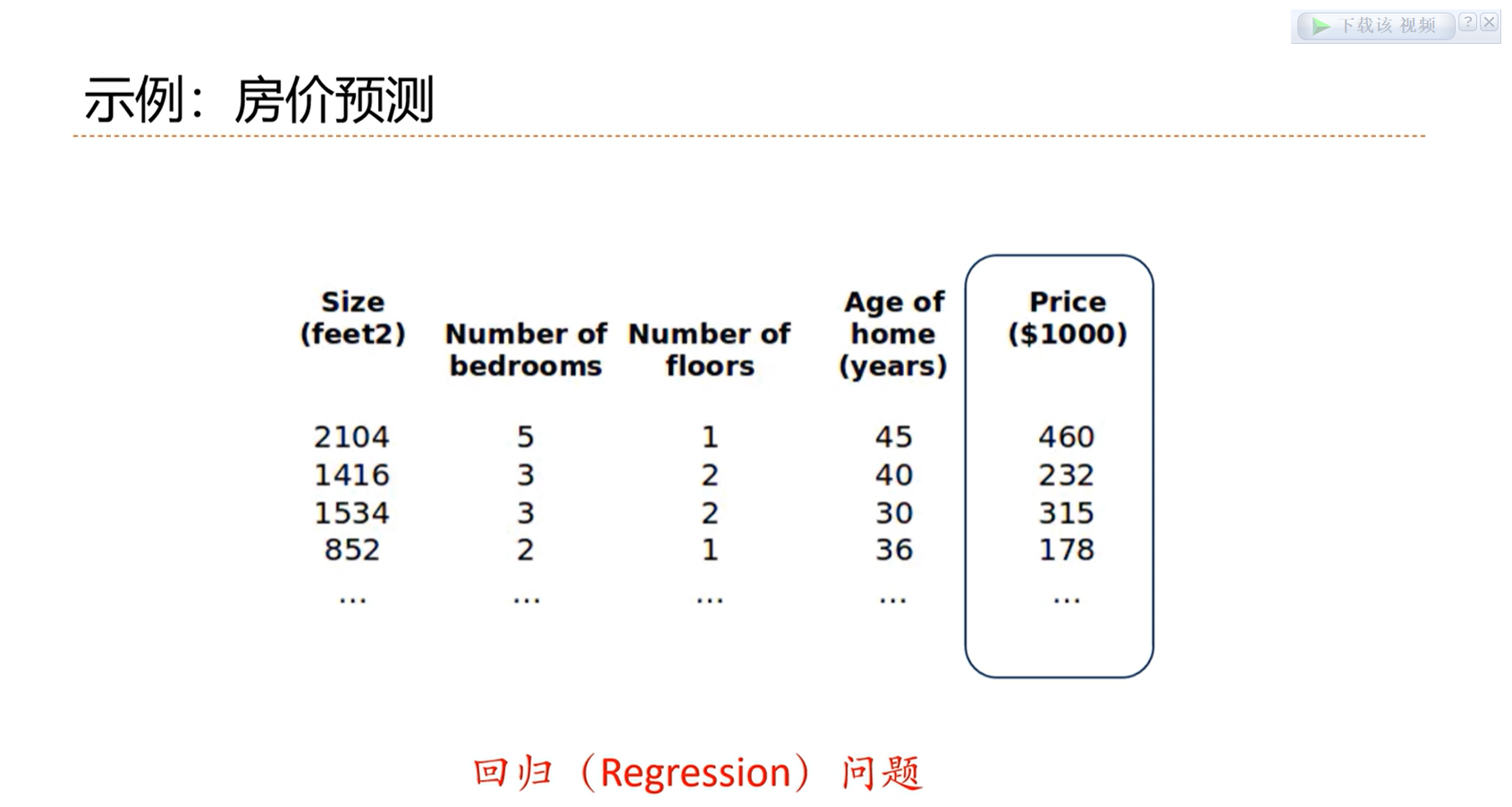

最终的结果是离散的,为分类问题
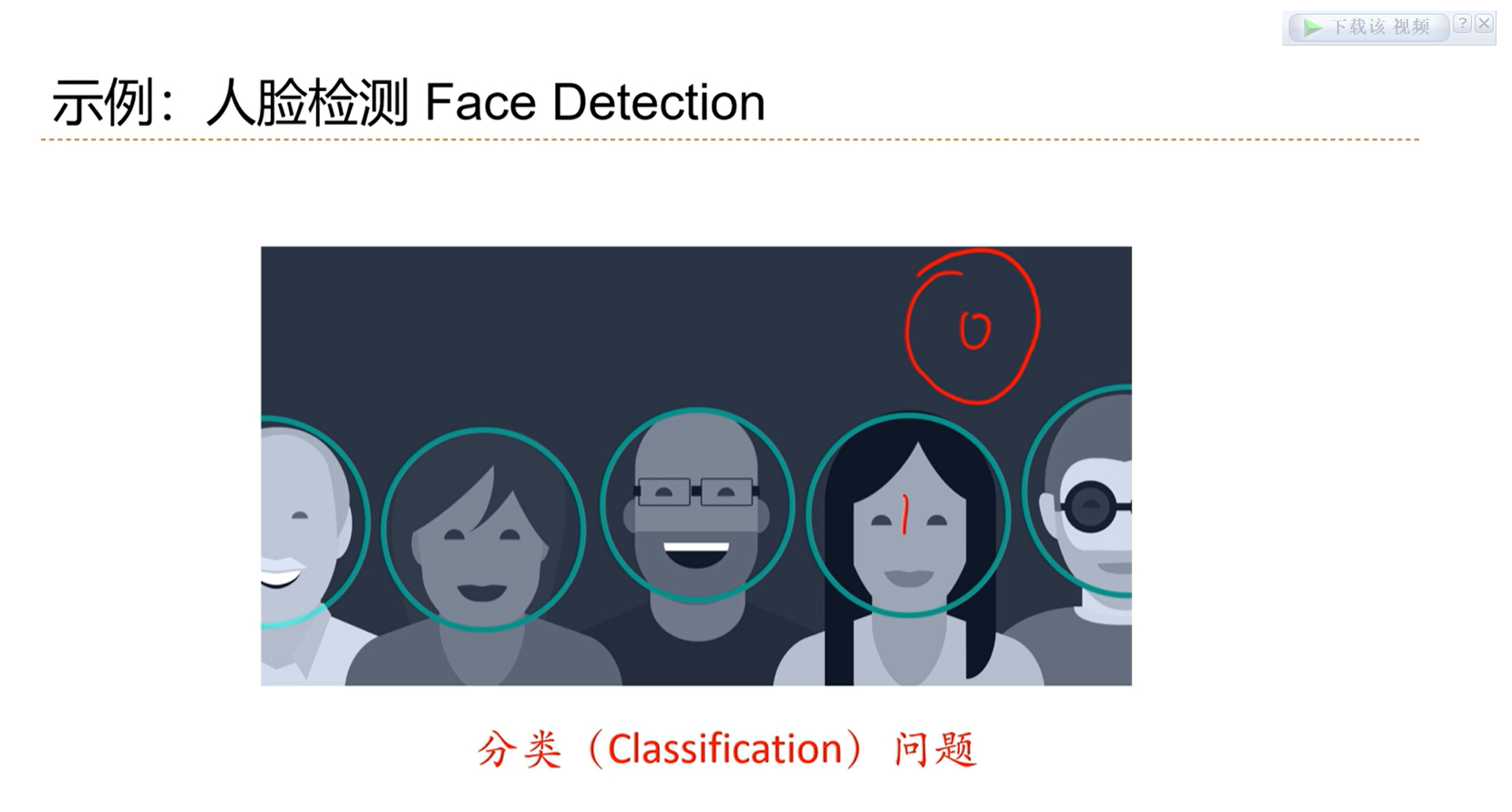
检测框内有没有人脸,二分类问题


聚类问题是无监督学习问题
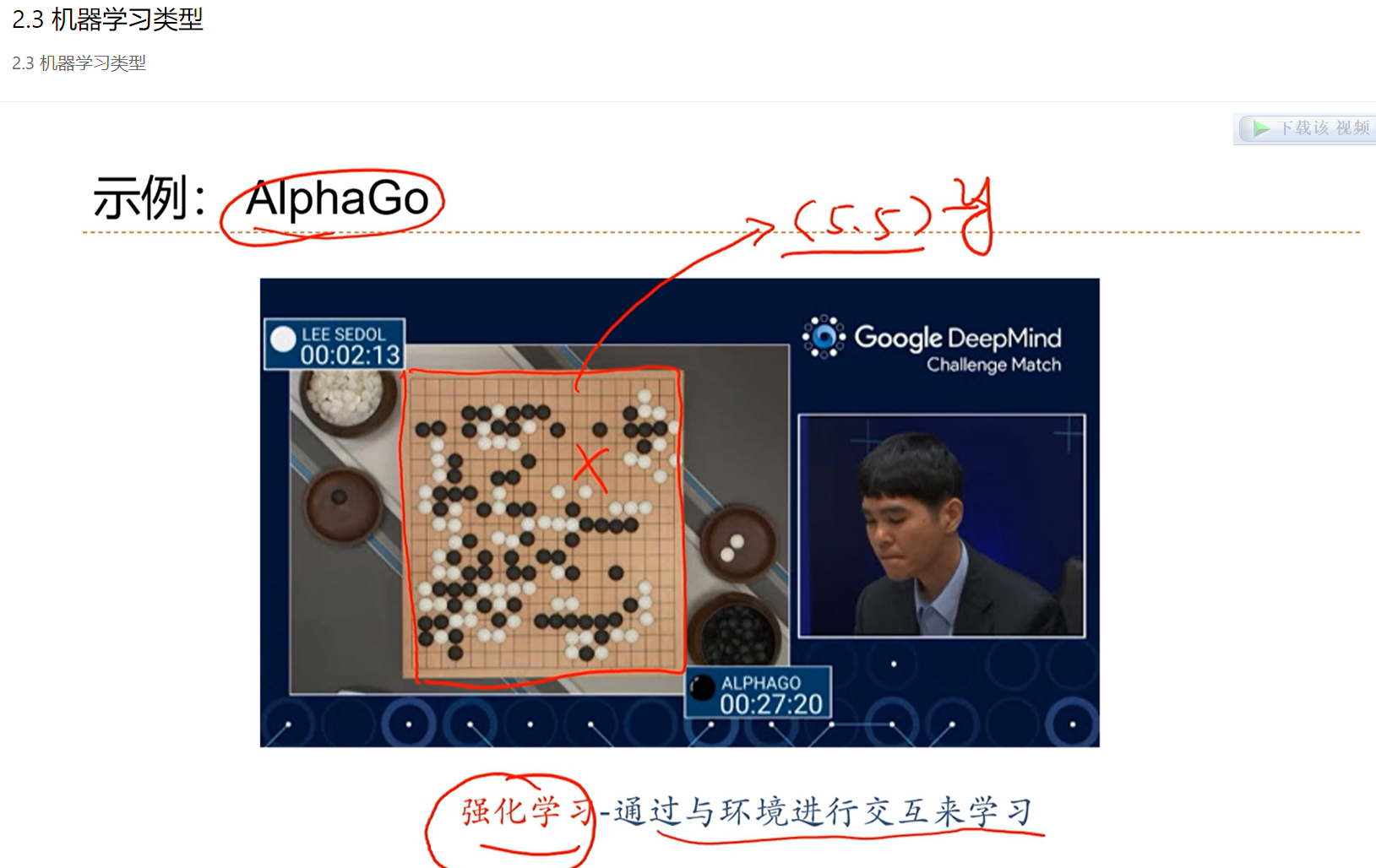
强化学习:尝试各种可能性,不断试错,看哪种可能性对最终的结果帮助最大,然后做出选择。


半监督学习:有一部分的数据是有标注的,一部分是没有标注的
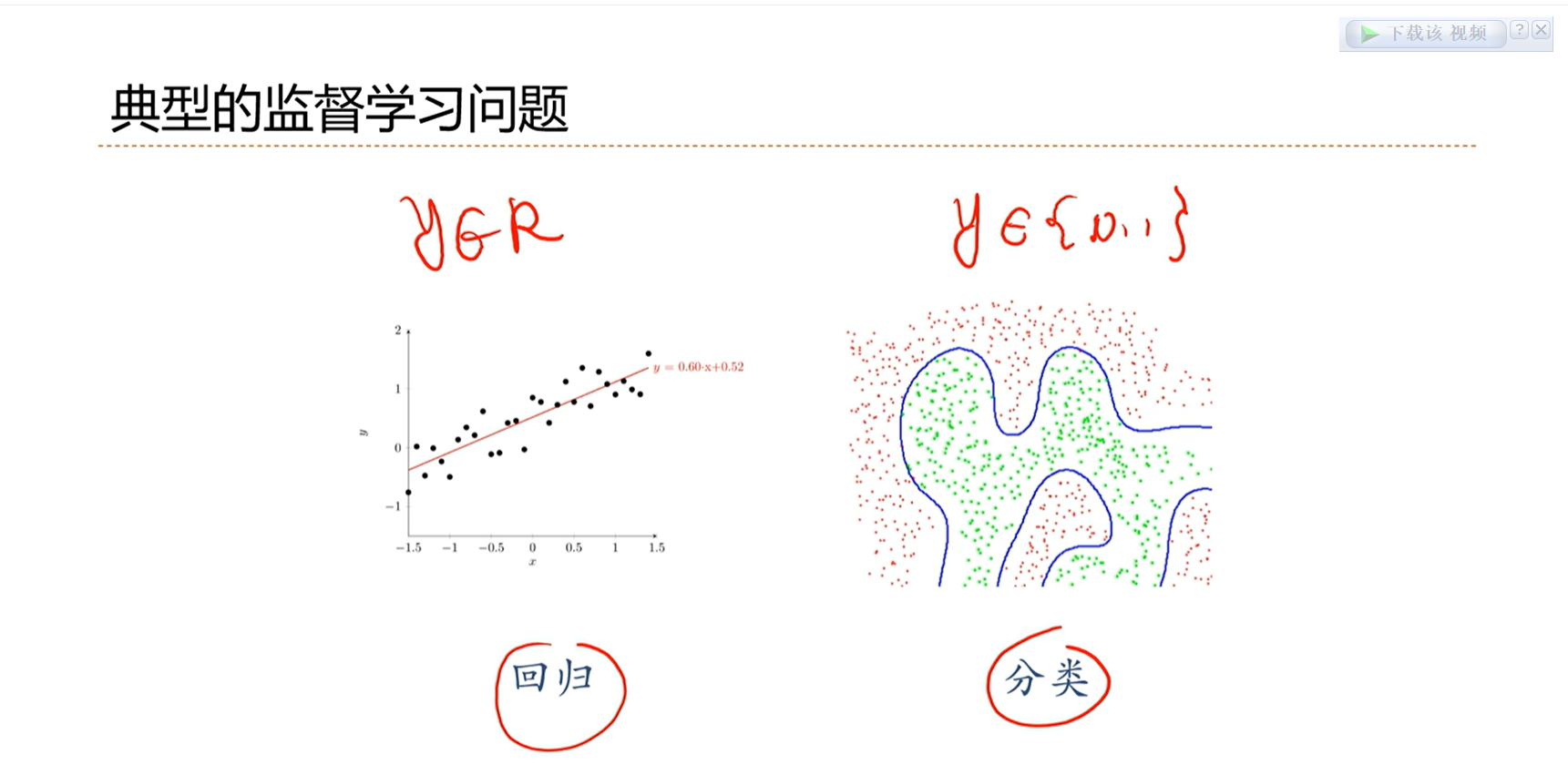
类型不同,因此学习的决策函数是有差异的、学习效果的衡量标准是不同的
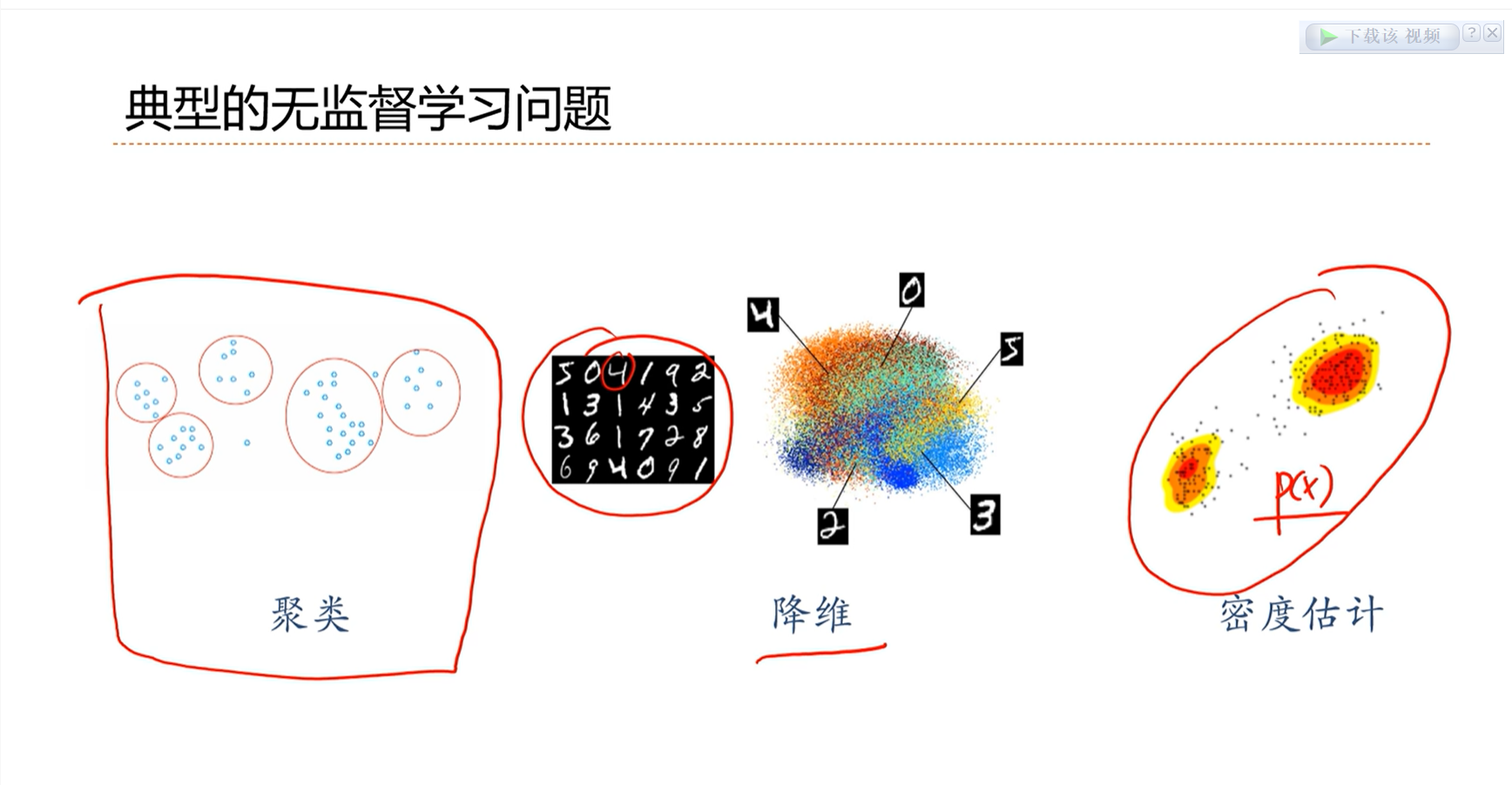
2.4 - 机器学习要素
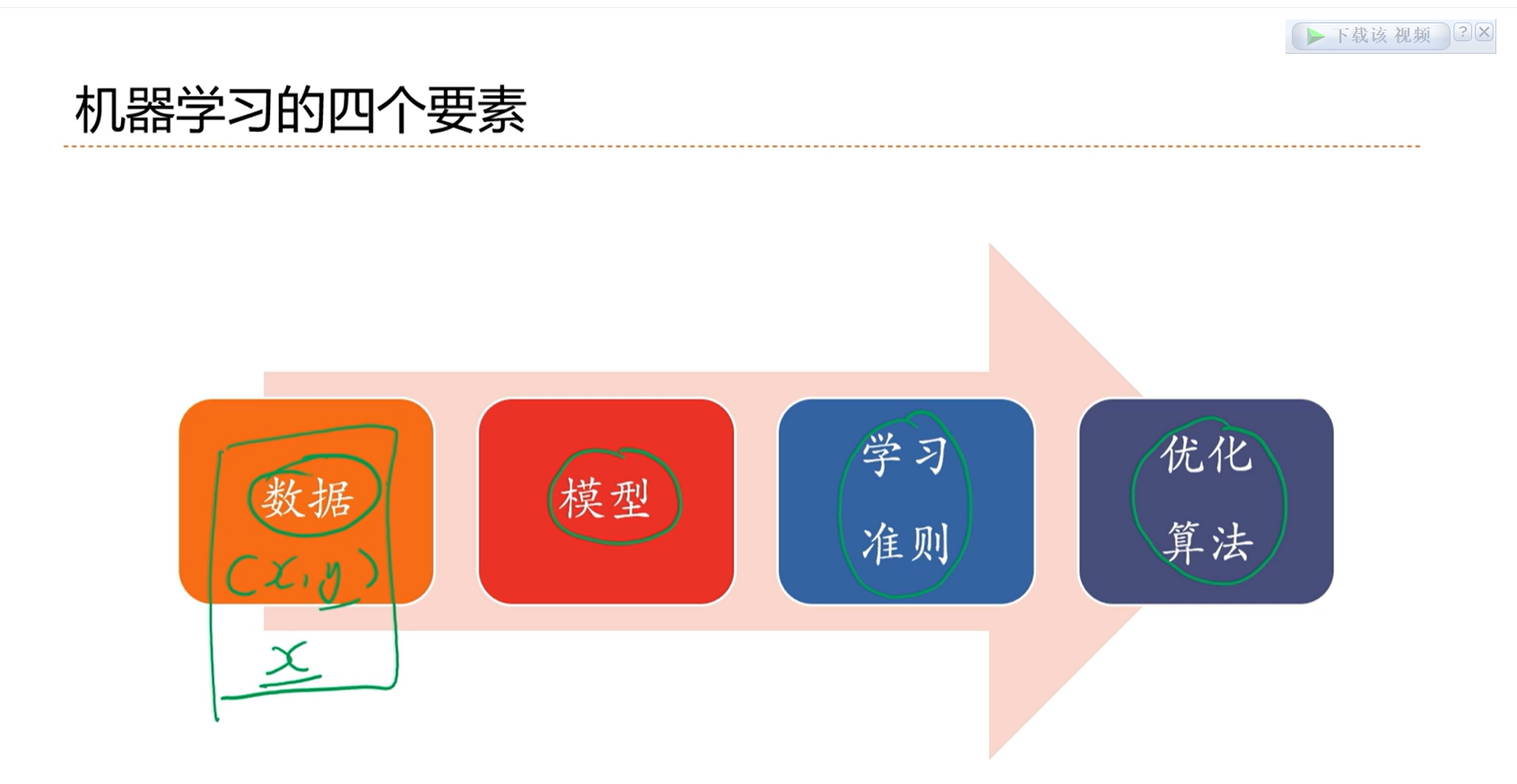

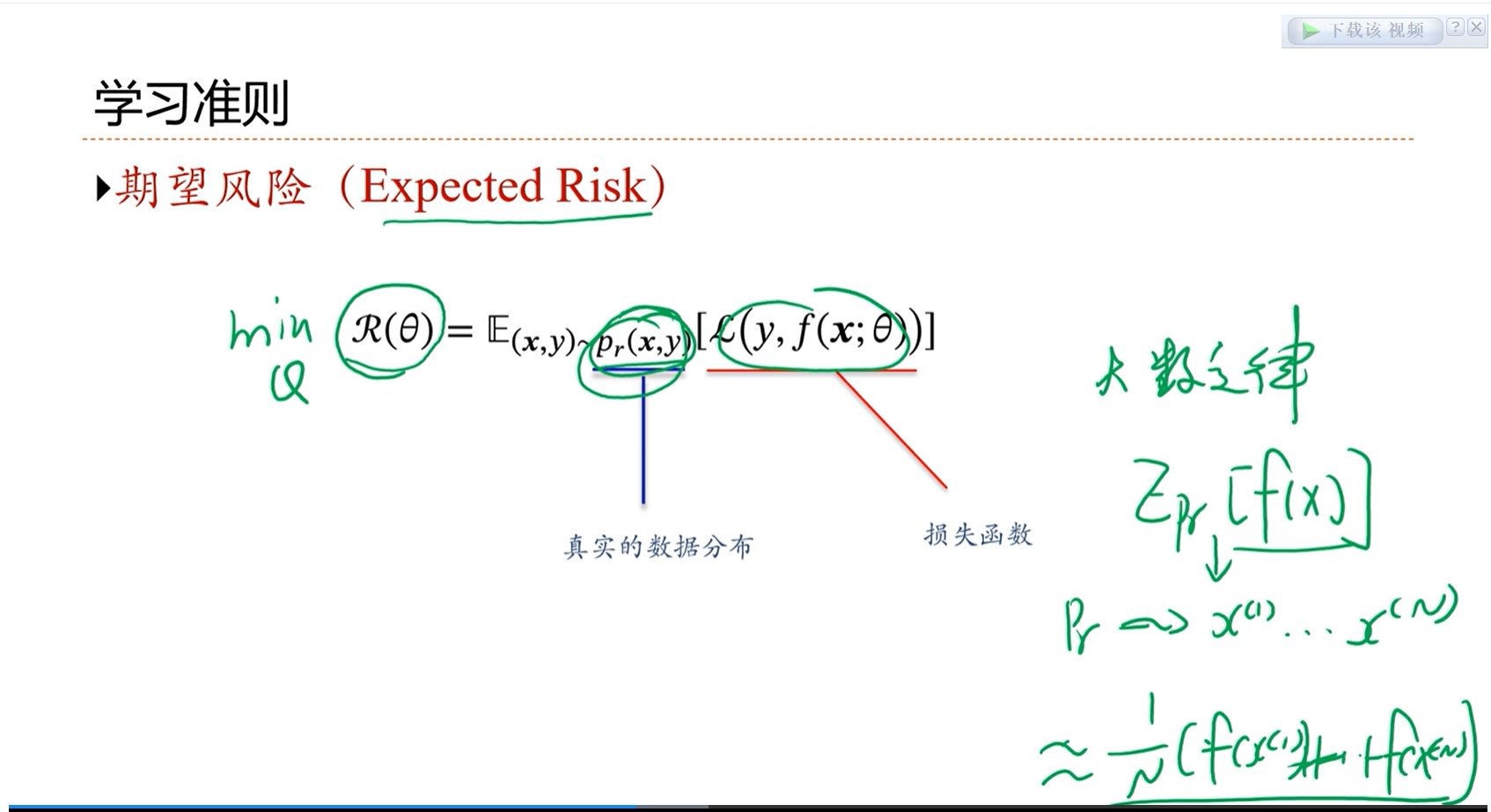
因为x、y之间的分布是未知的,因此期望风险是无法计算的。因此就通过大数定律来进行近似。
根据大数定律,当n趋向于无穷大的时候,经验风险逼近于期望风险。

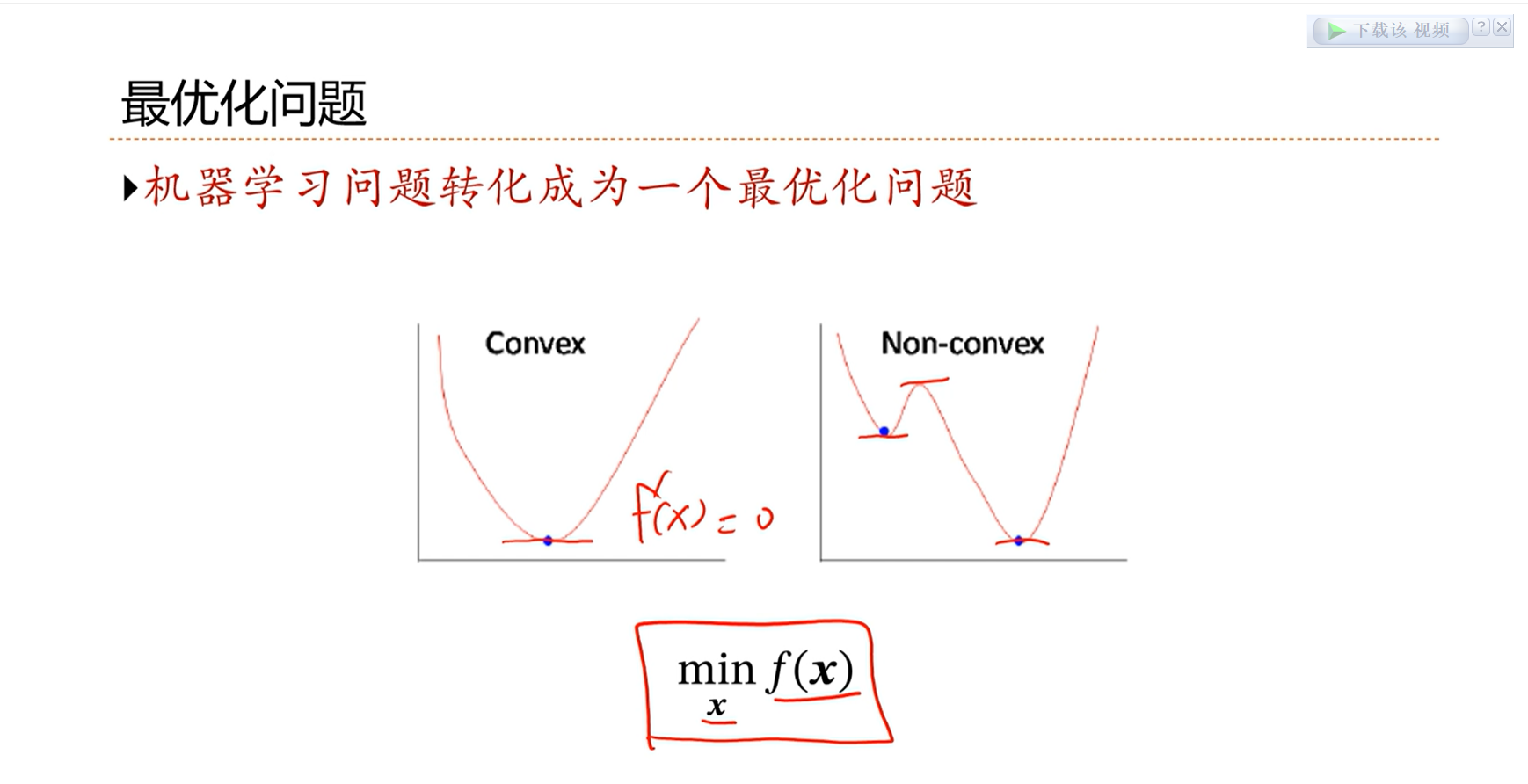
==最优化问题的解决方法1:==让极值点的导数等于0,找到极值点
凸优化问题,只有一个最优点,因此容易找到。
非凸优化问题,找到最优点是比较困难的。
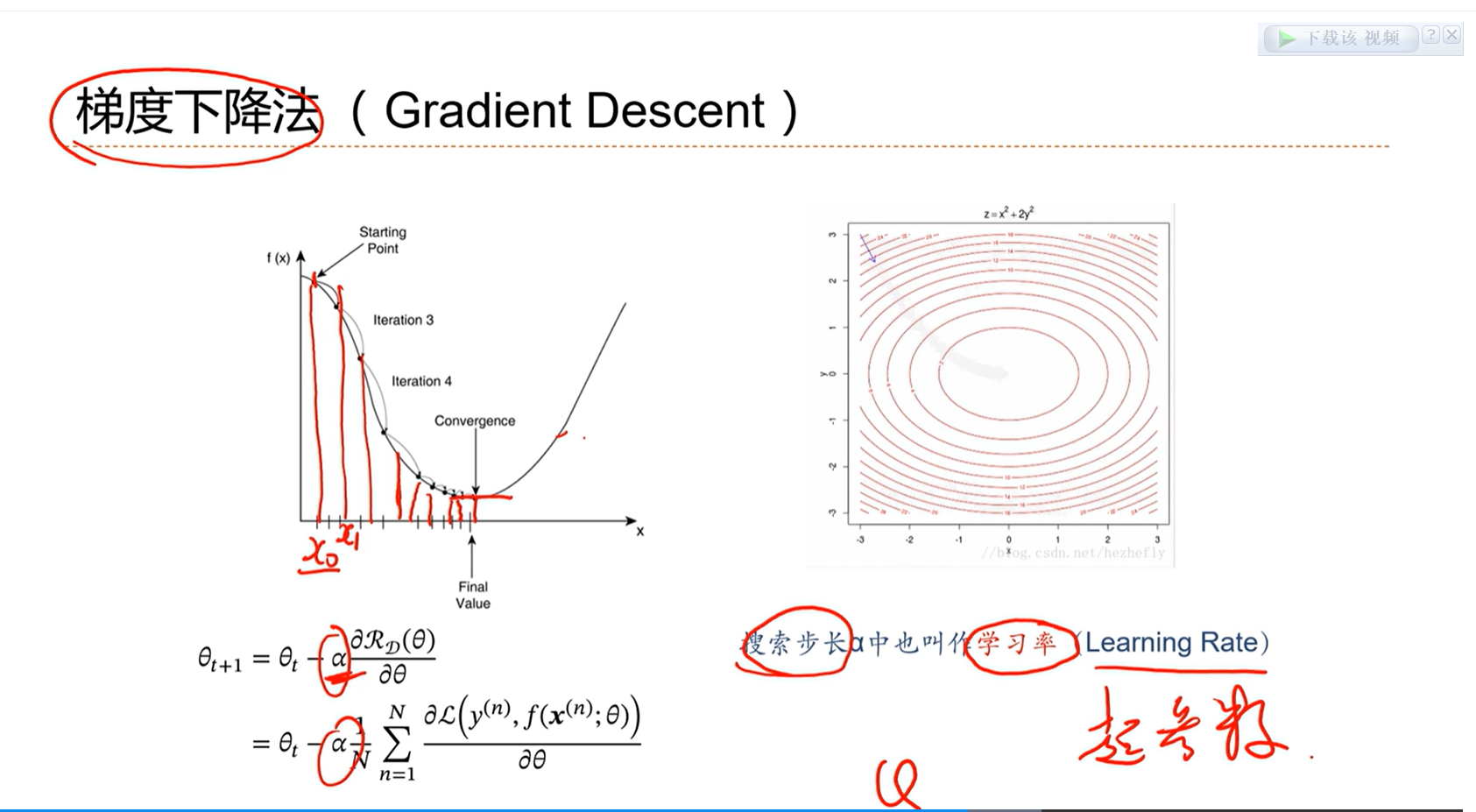
==最优化问题的解决方法2:==更具有一般性的解决方法,梯度下降法
梯度下降算法是一个迭代的方法,给任意一个起始点,计算这个点的梯度,沿着这个梯度的反方向走,那么这个损失值一把来说会是下降的。
如果走的步长不是太大,那么一定会收敛到一个极值点。
在梯度下降算法中,有一个参数 α 用来表示每次走的步长。在机器学习中,也叫学习率。
α 这是一个非常重要的超参数。对于损失函数中的参数,是可学习的。对于 α 是无法学习的,需要人为的去选择,所以叫超参数。
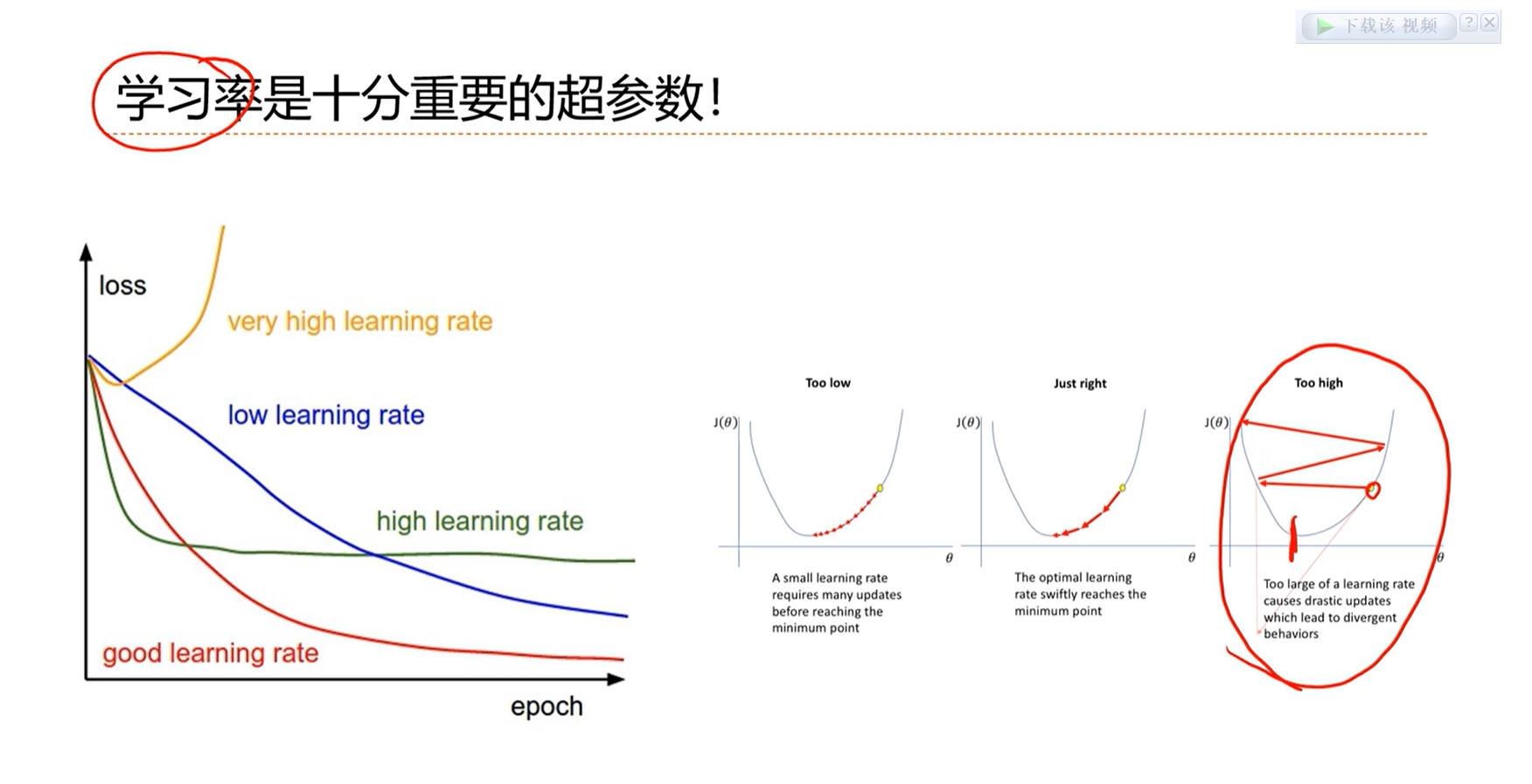
学习率太大的话,就来回震荡,永远不收敛;学习率太小的话,就学的很慢,或者陷入局部最优。
自适应的学习率是动态变化的,比较理想。
==梯度下降法的变种:随机梯度下降算法==
不需要在每个样本上采集梯度,而是随机的选择一个样本采集梯度,更新参数就可以了。


随机梯度下降算法的缺点是无法充分利用计算机的并行能力,因此一个折中的方法是小批量随机梯度下降法。
批量k的选择一般是将显卡的内存用满就可以了,最大程度的发挥计算机的并行计算能力。
目前大部分的机器学习算法中,通常是使用mini-batch

问题1:
在随机梯度下降法中,为了避免某些样本始终采集不到,因此每次训练完一轮后,对所有的样本再次打乱随机排序,这样就避免了一些样本始终采集不到的问题。
问题2:什么时候判断SGD已经学习好了
通常停止迭代的标准是:设定另外一个验证集V,在验证集上的错误率不再下降,那么认为这个训练集已经收敛了
2.5 - 泛化与正则化
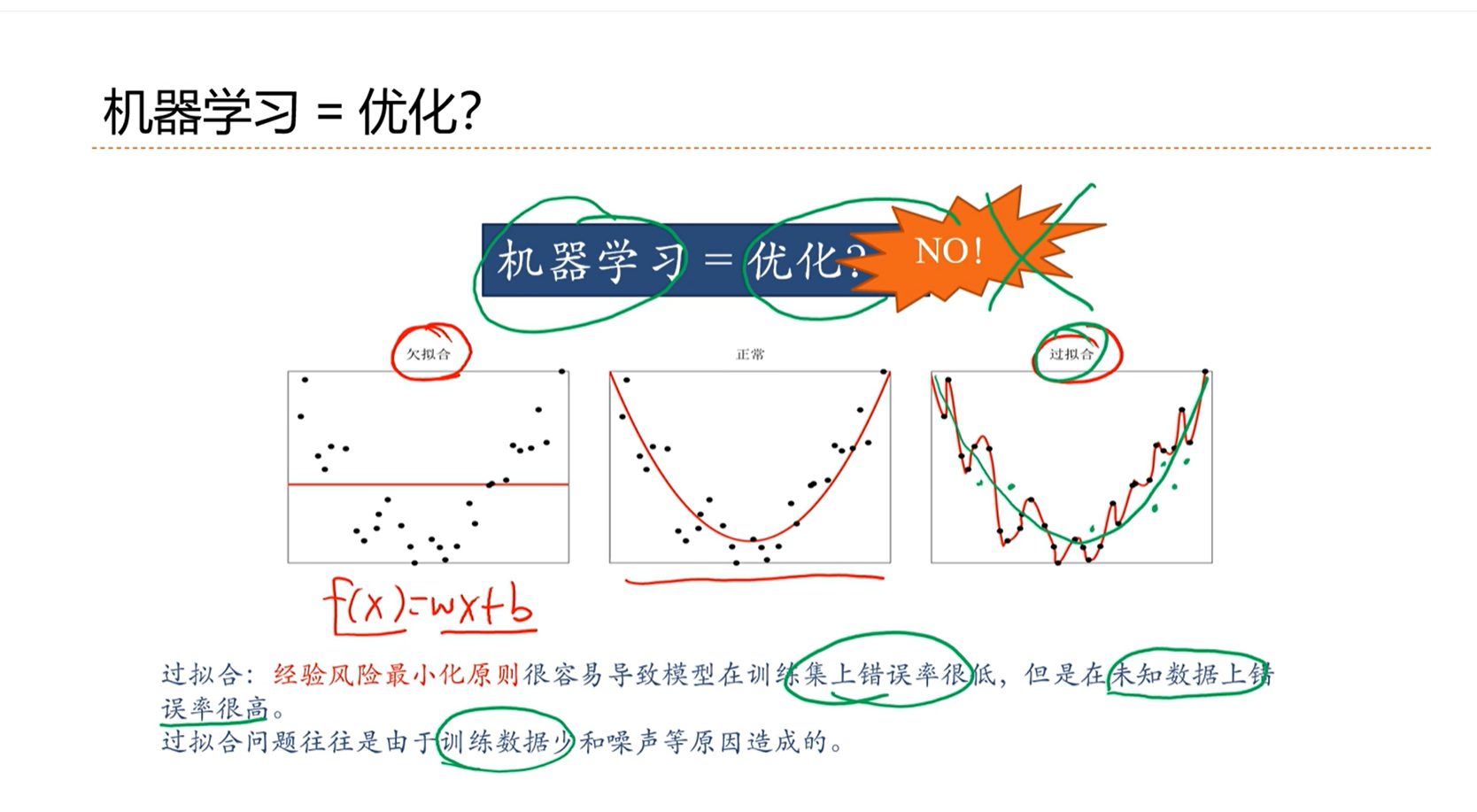
↑ :机器学习问题不是绝对等价于优化问题。在训练数据少和噪声的情况下最优的优化会导致过拟合。
欠拟合难问题:可能是由于模型能力不够,比如本来问题是非线性的,但是我们使用线性的模型去拟合,就会导致欠拟合问题。
机器学习问题关注的不是在训练集上的错误率,而是在整个期望上错误率,即期望风险。
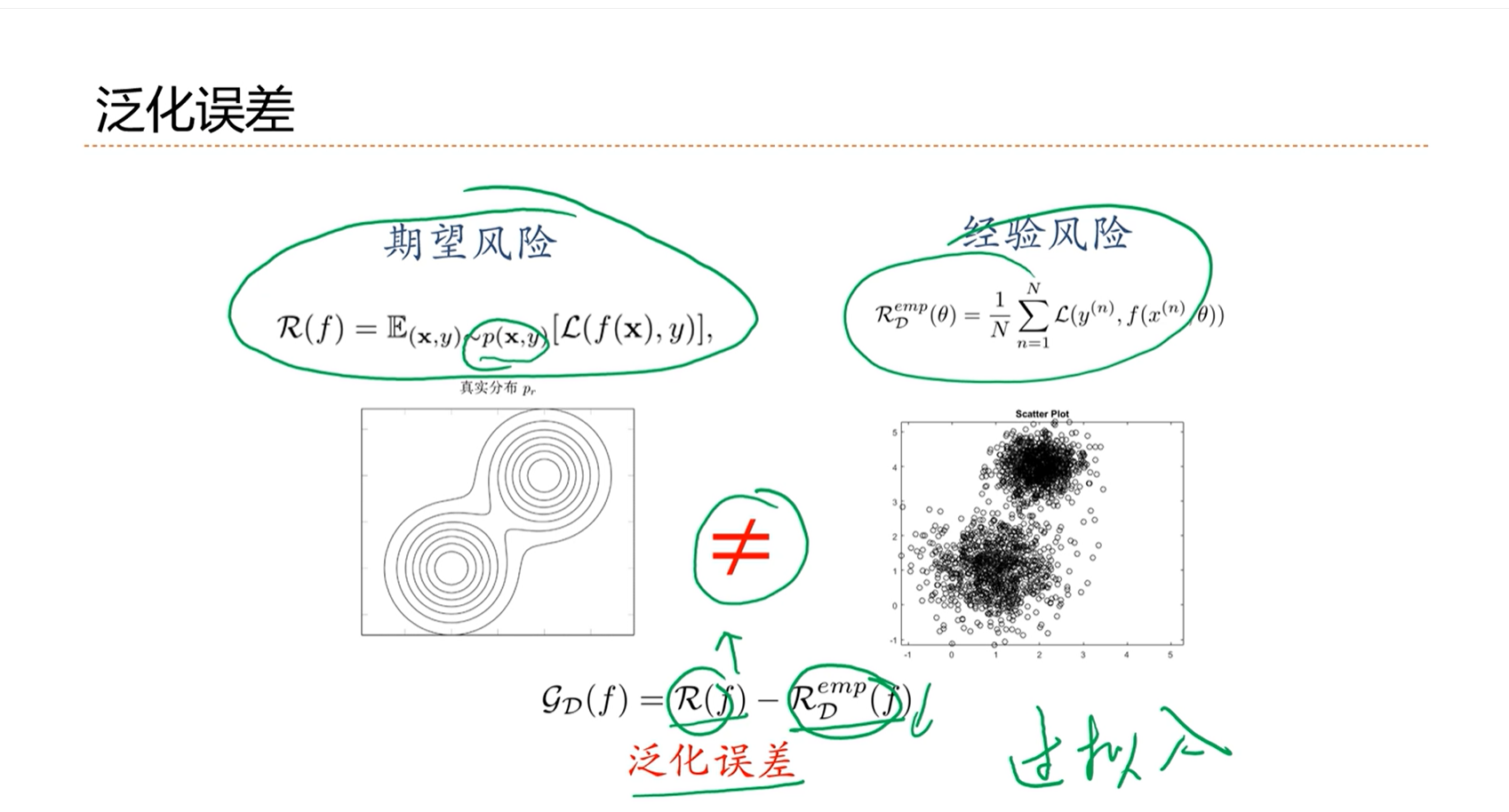
期望风险大,经验风险很小,这时就发生了过拟合。
期望风险小,经验风险很大,这时就发生了欠拟合。
机器学习的真正目标是期望期望风险和经验风险都低。
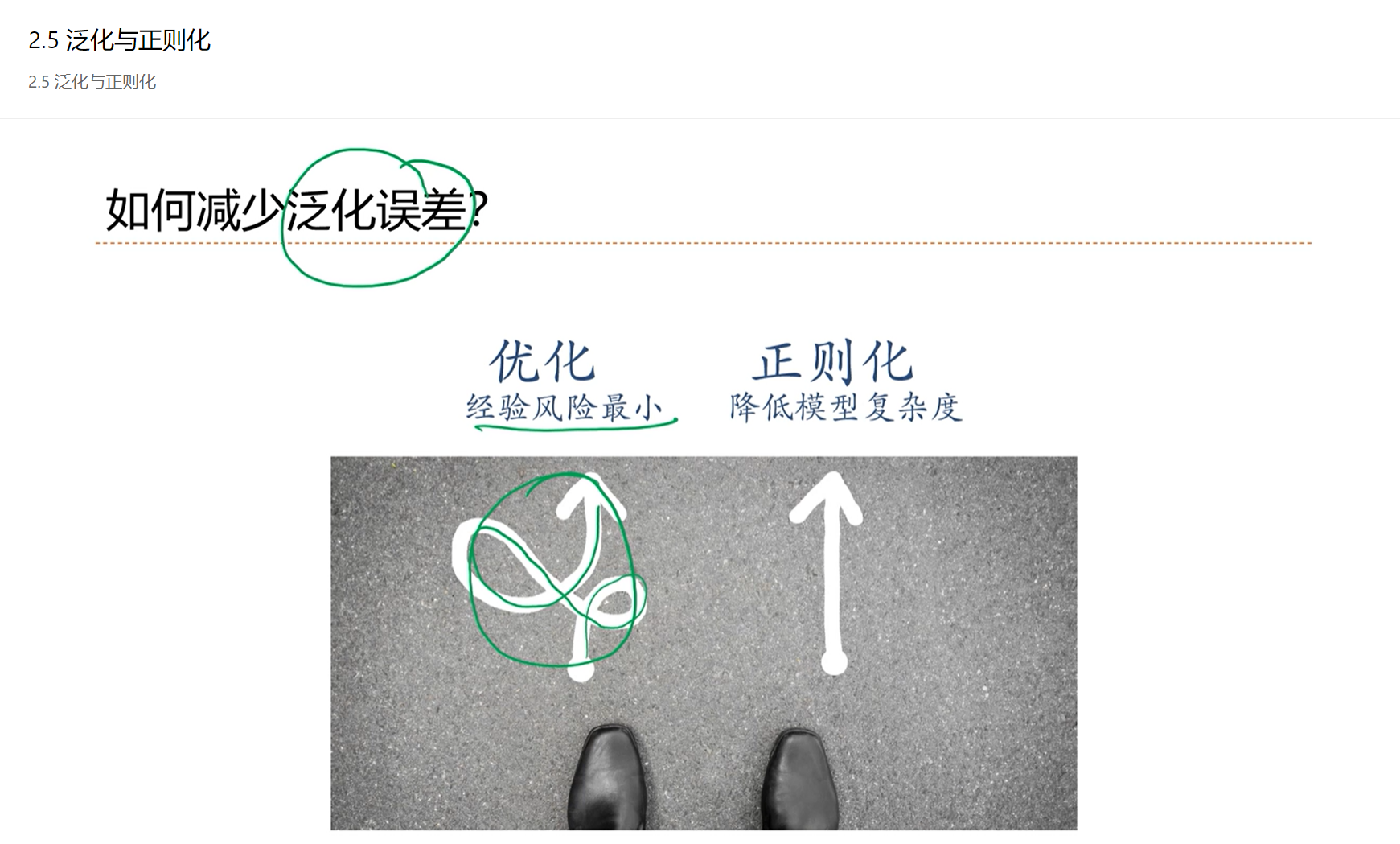
优化的时候,可能导致过拟合,即训练出来的模型复杂度很高。
通过一些手段,比如正则化,期望模型不要那么拟合,从而降低模型的复杂度。
正则化是降低泛化误差的一个有效手段。
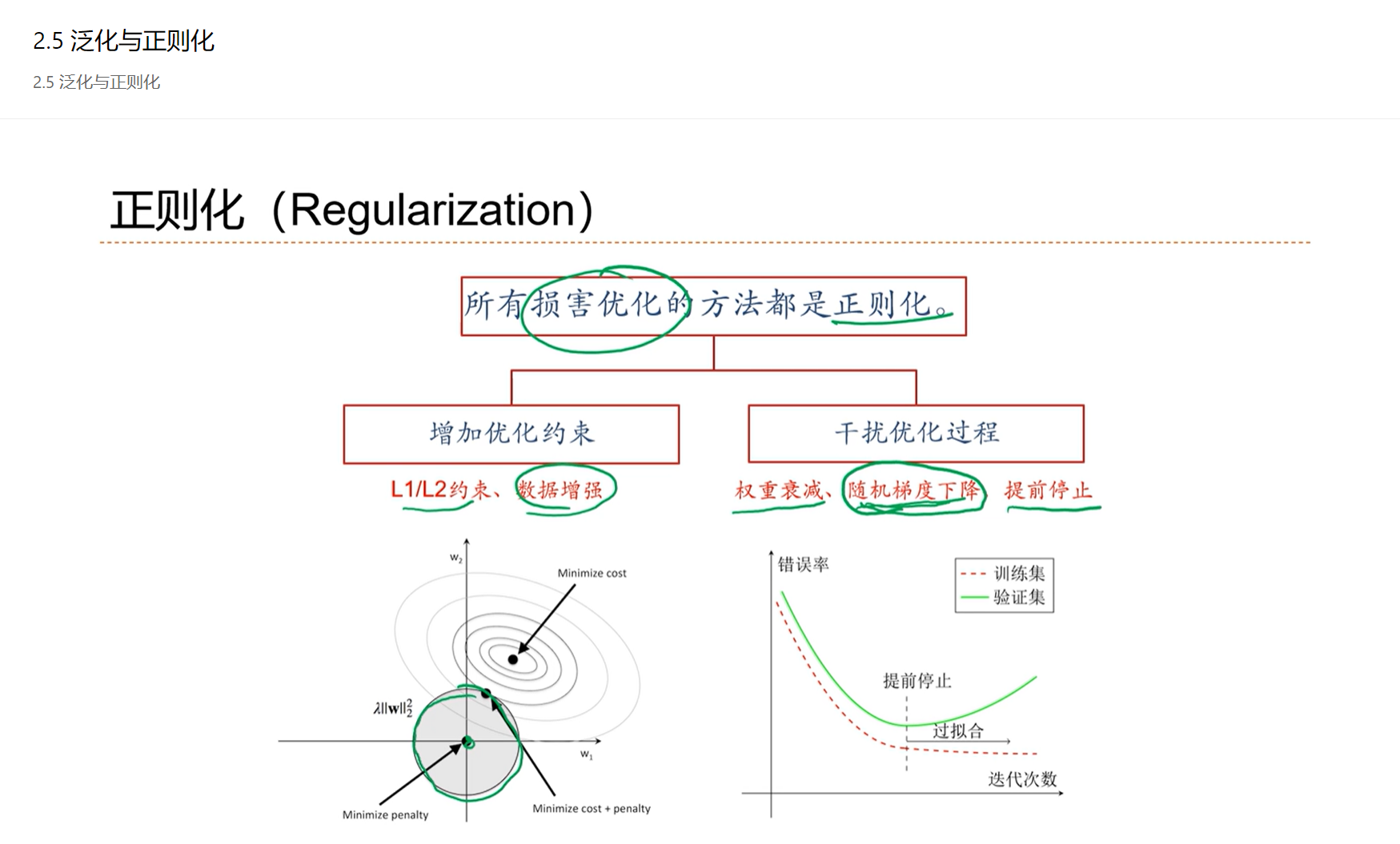
验证集和训练集是独立的,都是独立同分布采样的
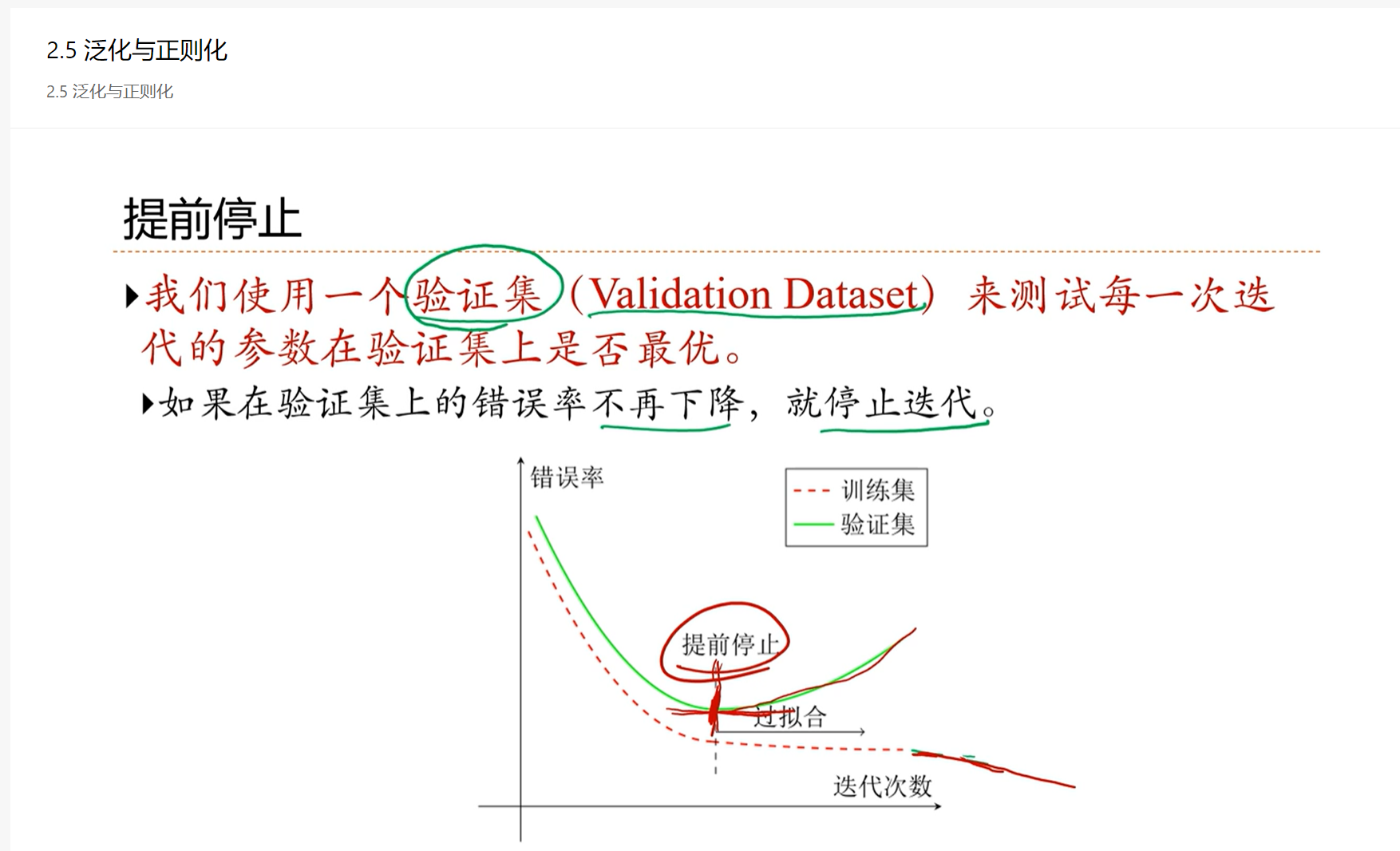
提前停止是目前在机器学习上,配合SGD用的最多的一种正则化方法

2.6 - 线性回归
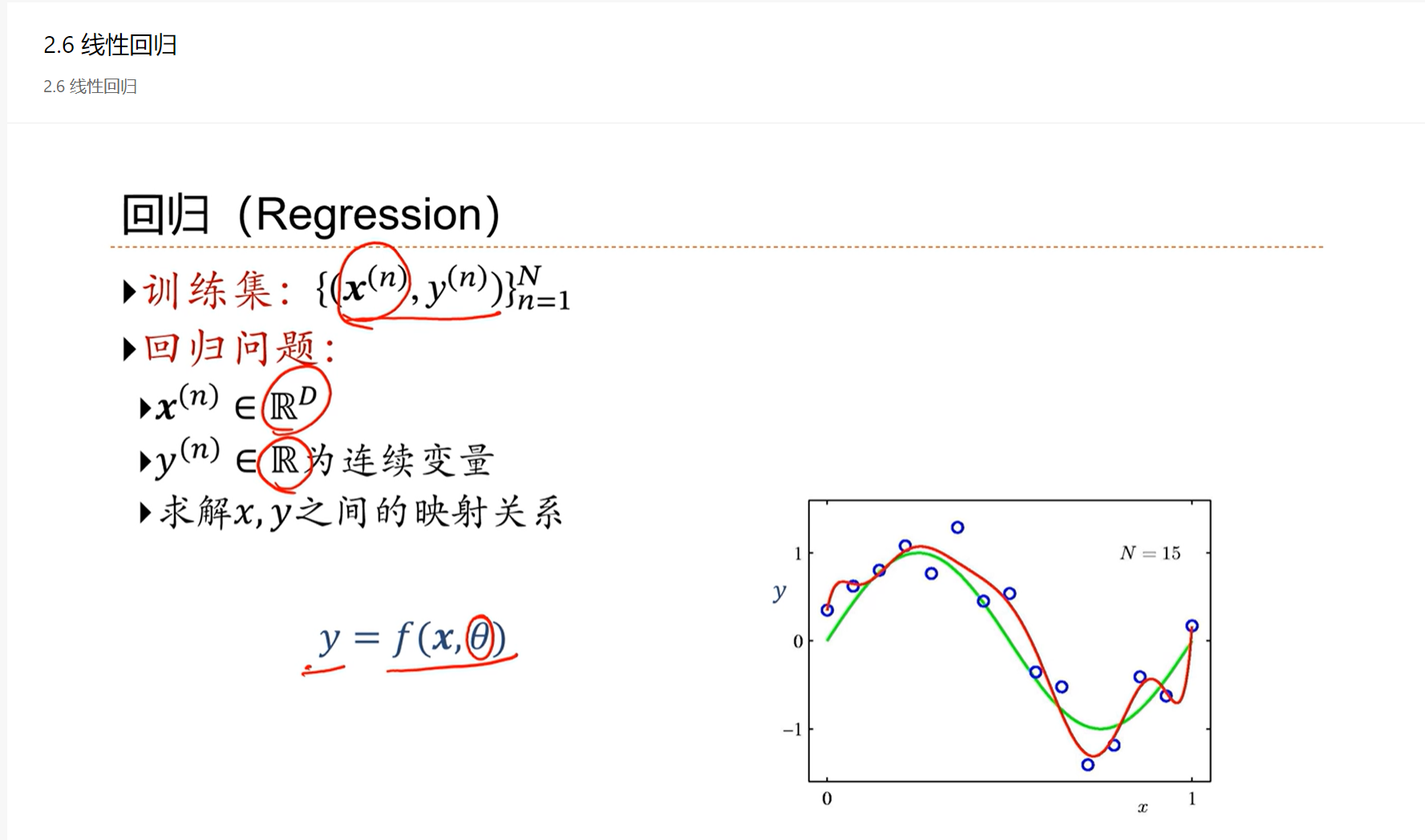
输入是一个低维的向量(R的右上角有D),输出是一个标量(R的右上角为1次方)。
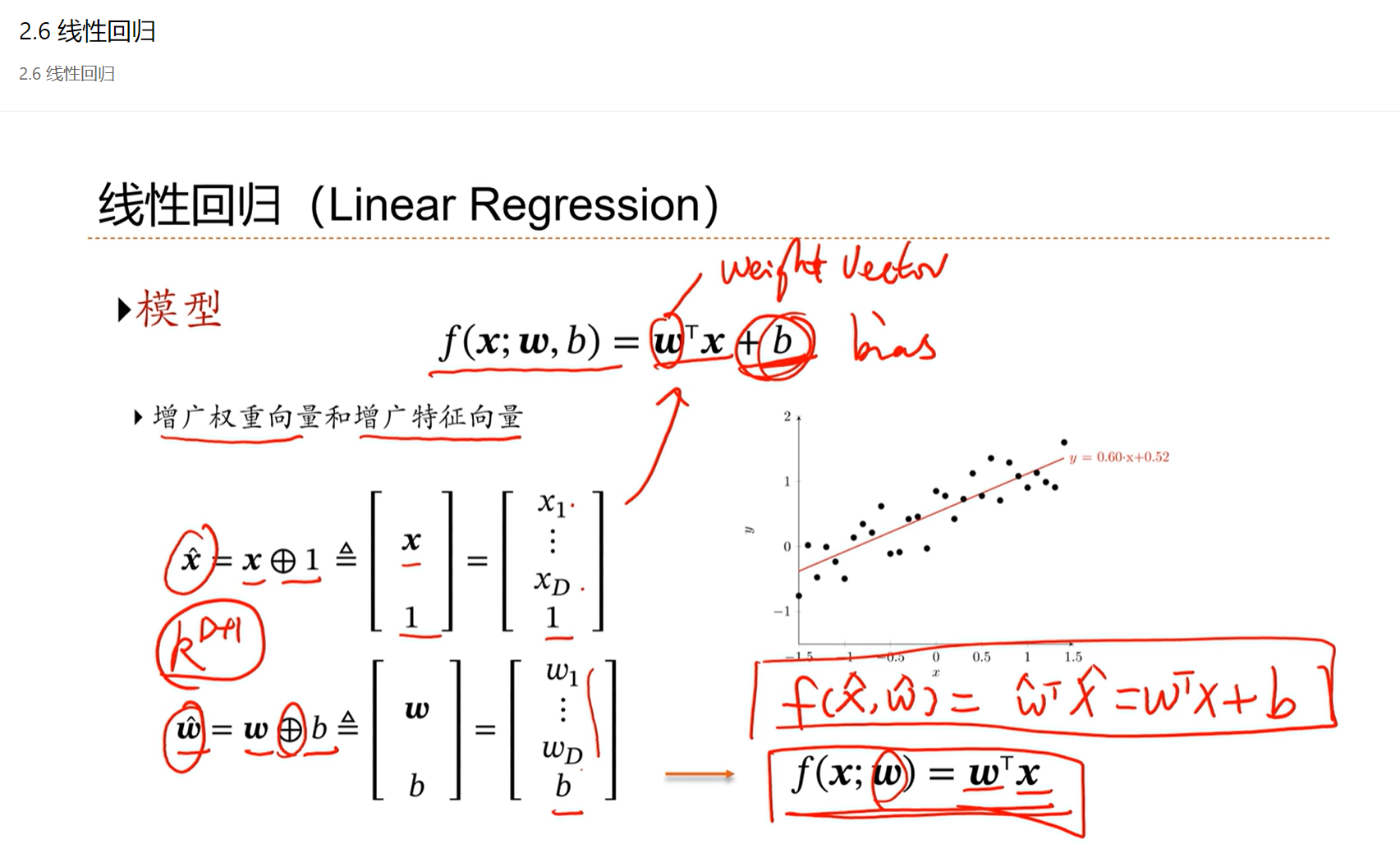


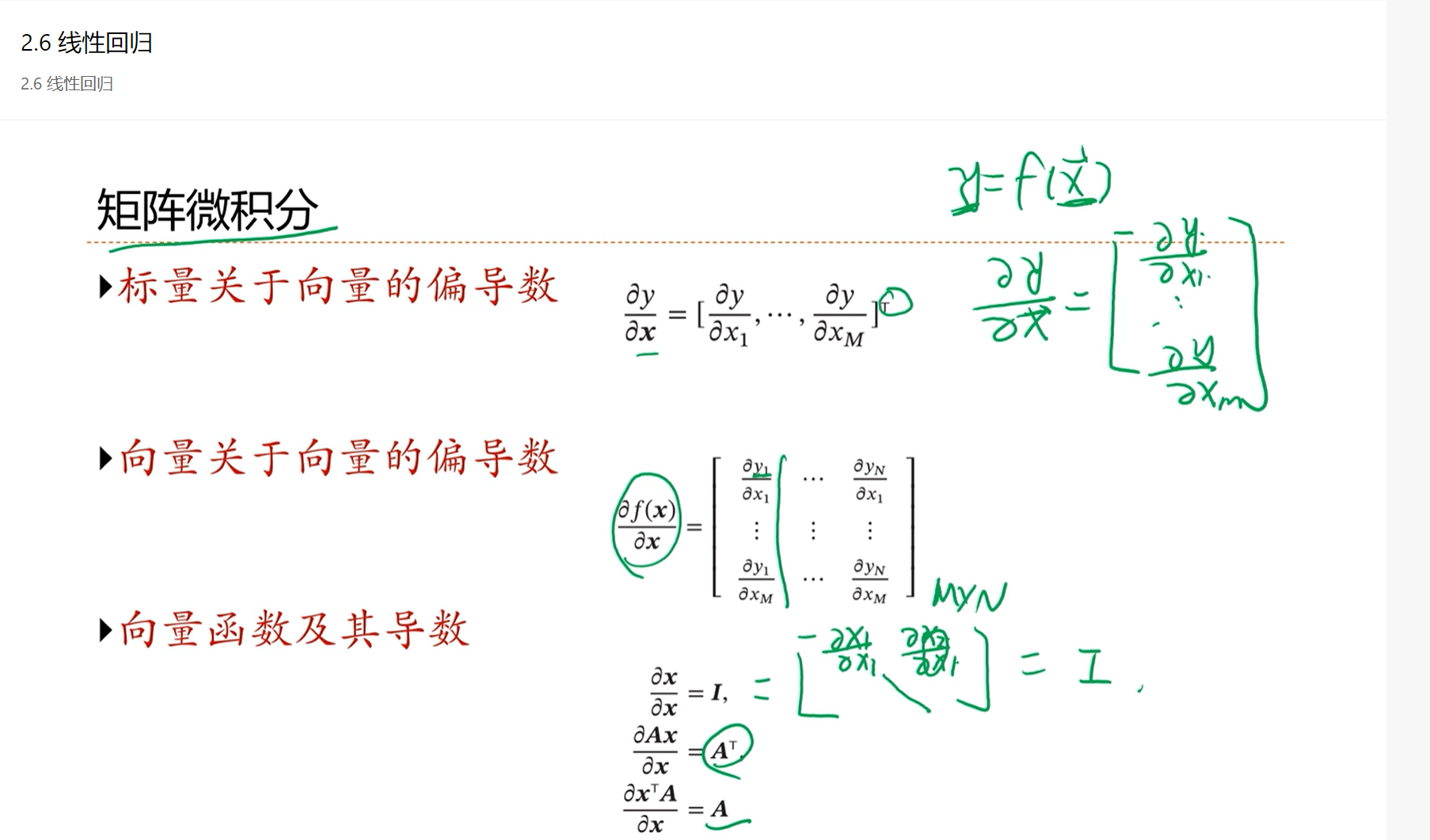

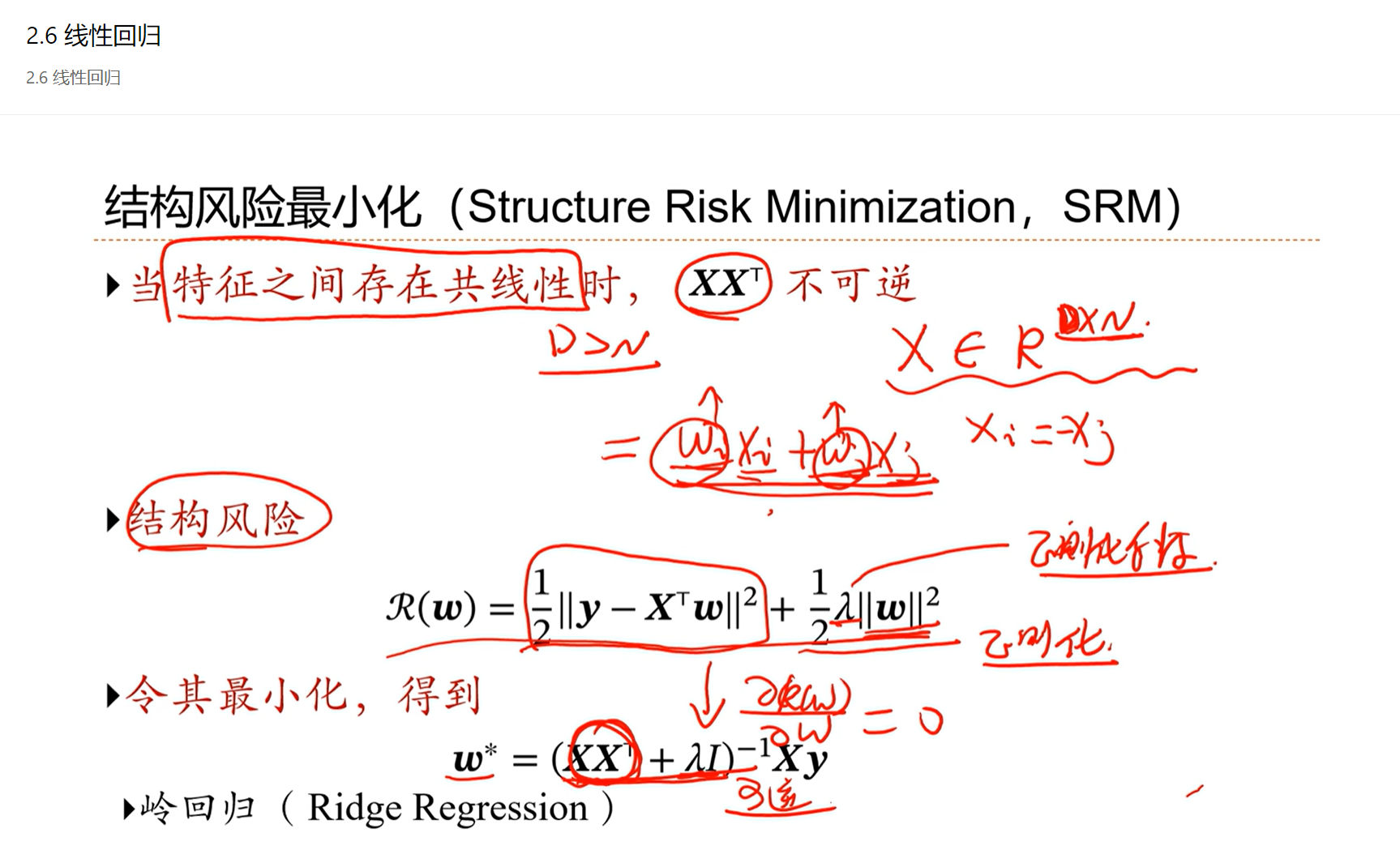
为了防止经验风险输入x之间因为存在特征的冗余导致最终的解不稳定的问题,因此引入结构风险,后半部分就是正则化项。
λ 是正则化系数,是人为设置的一个超参数,λ 越大对 w 的限制越大。
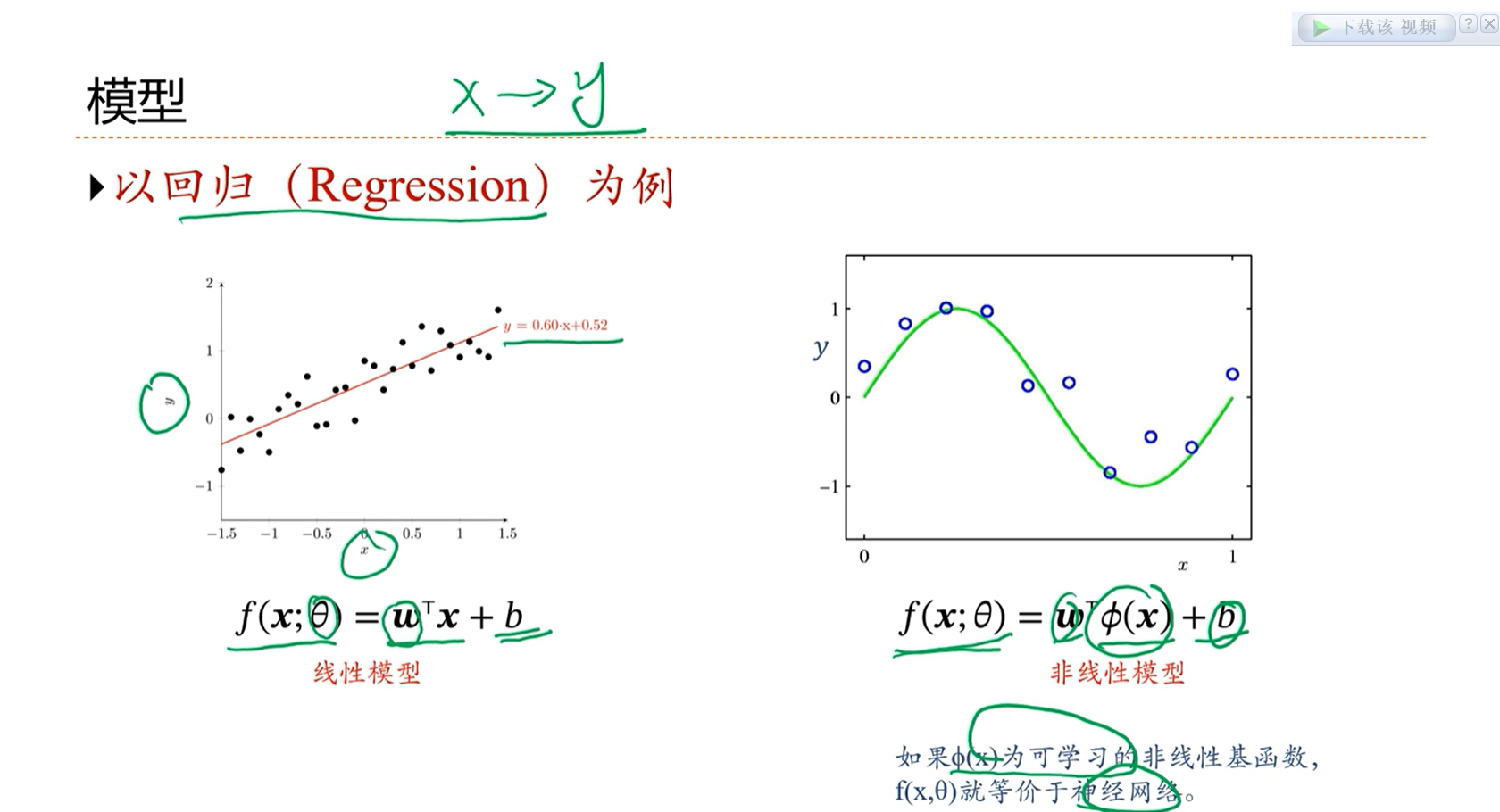
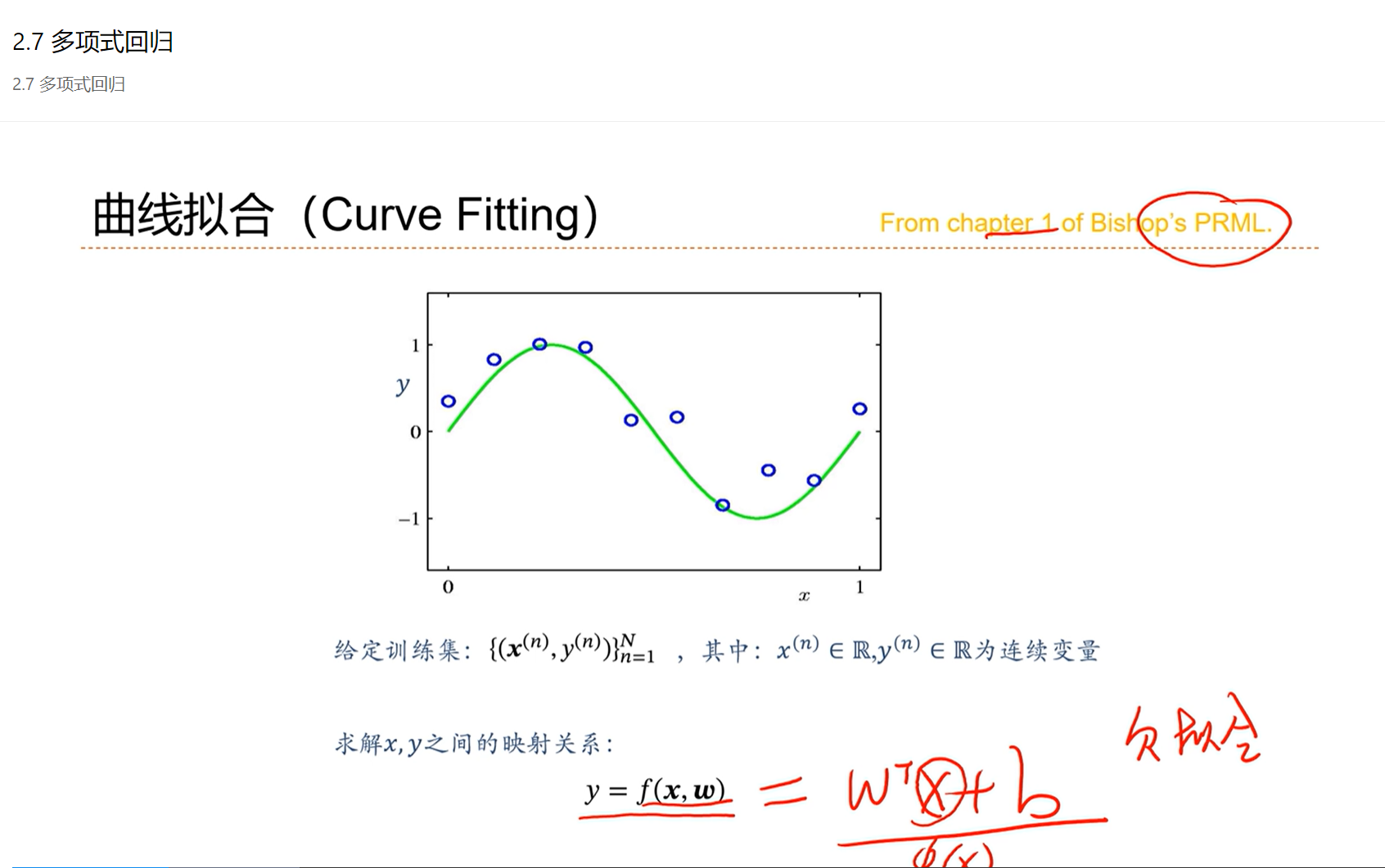
2.7 - 多项式回归
多项式回归是线性回归的非线性形式。
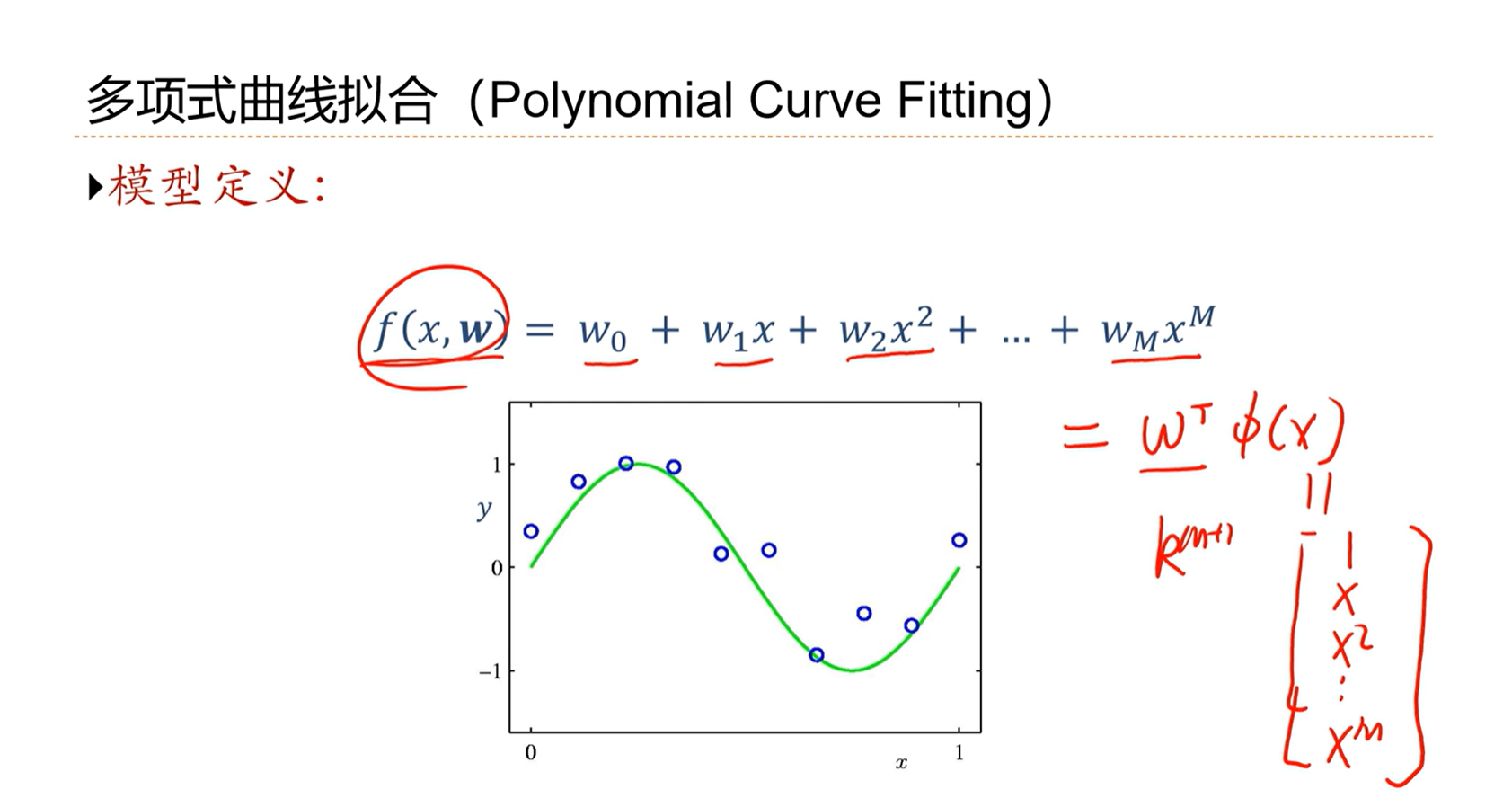
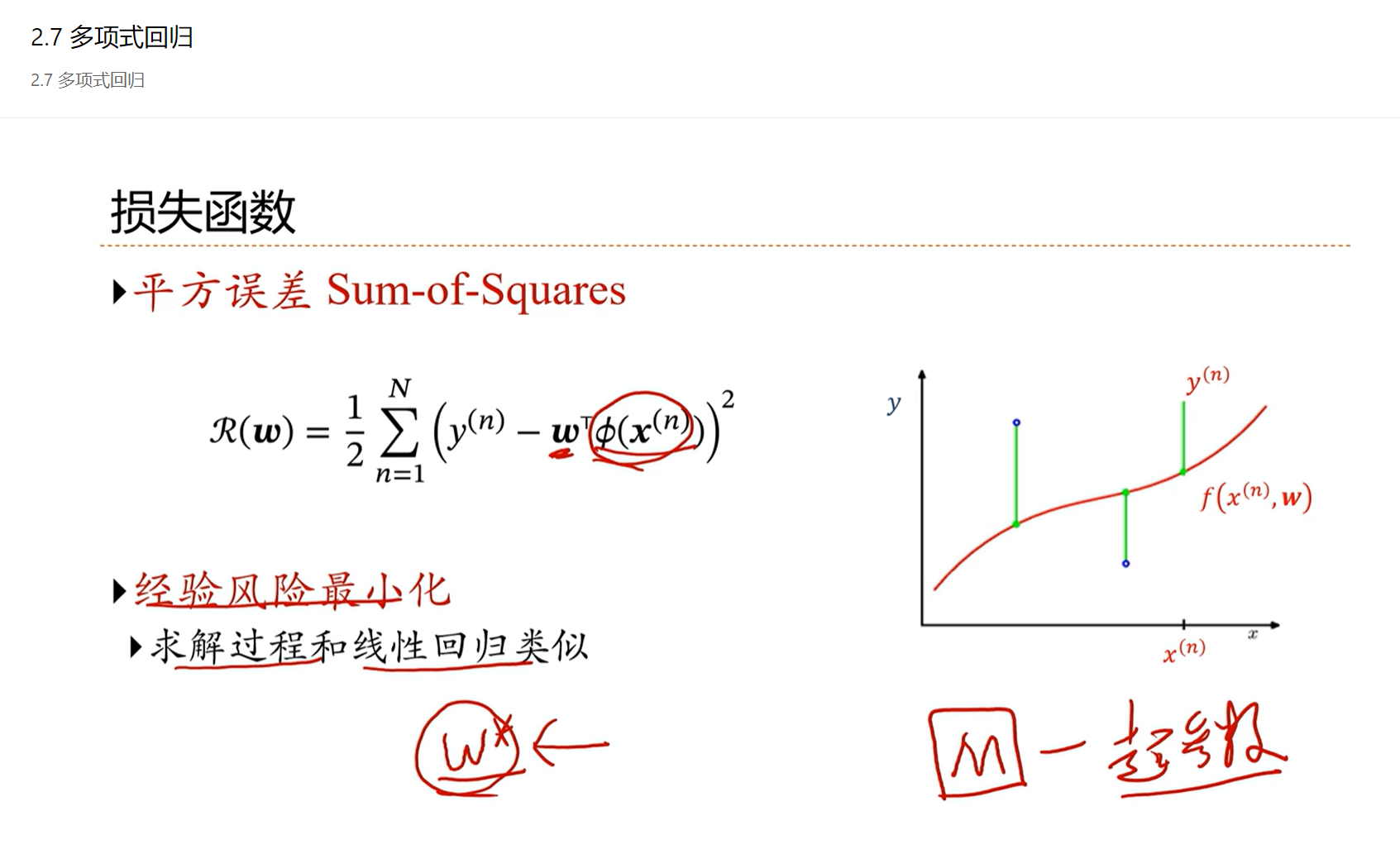
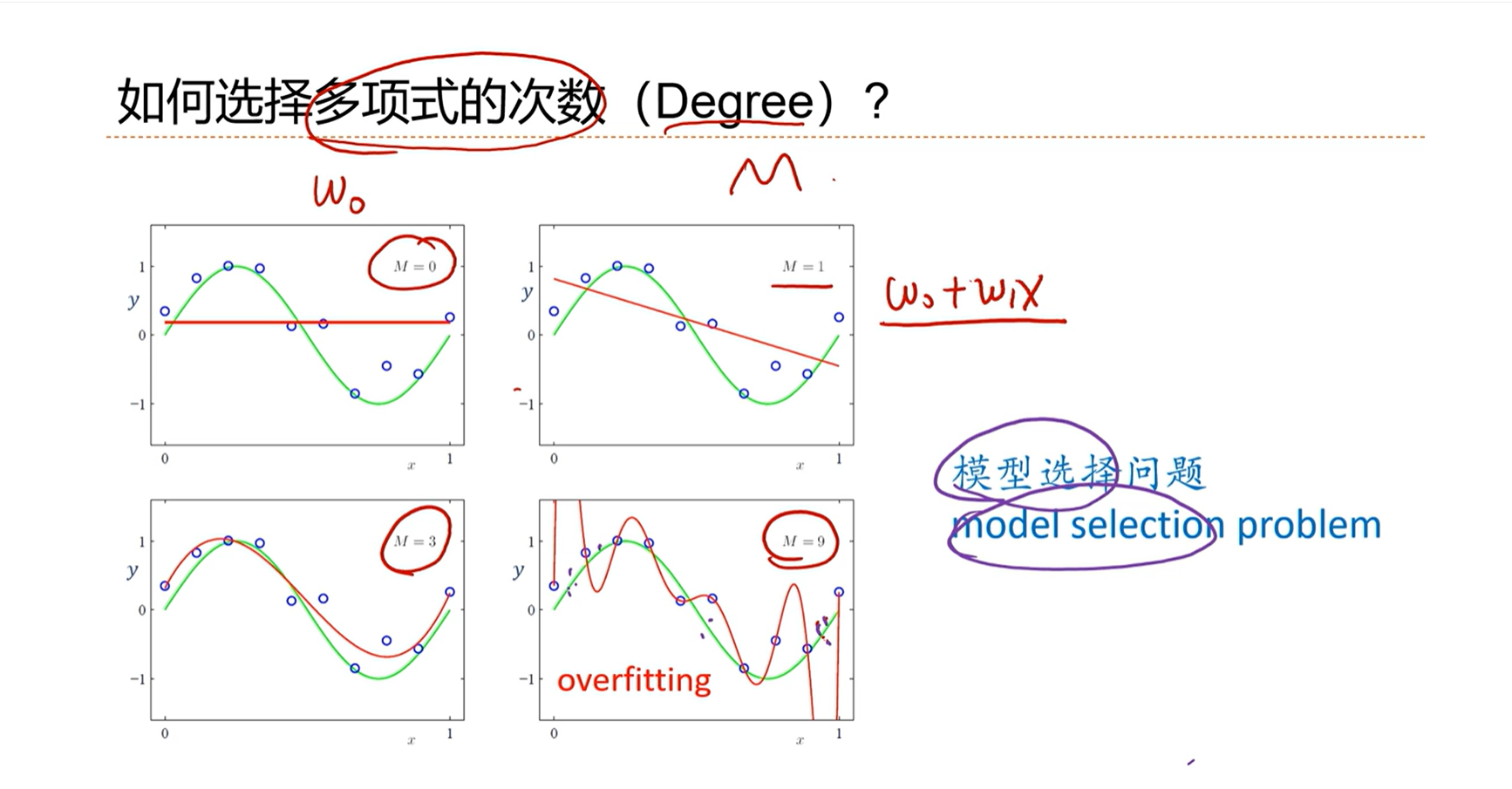
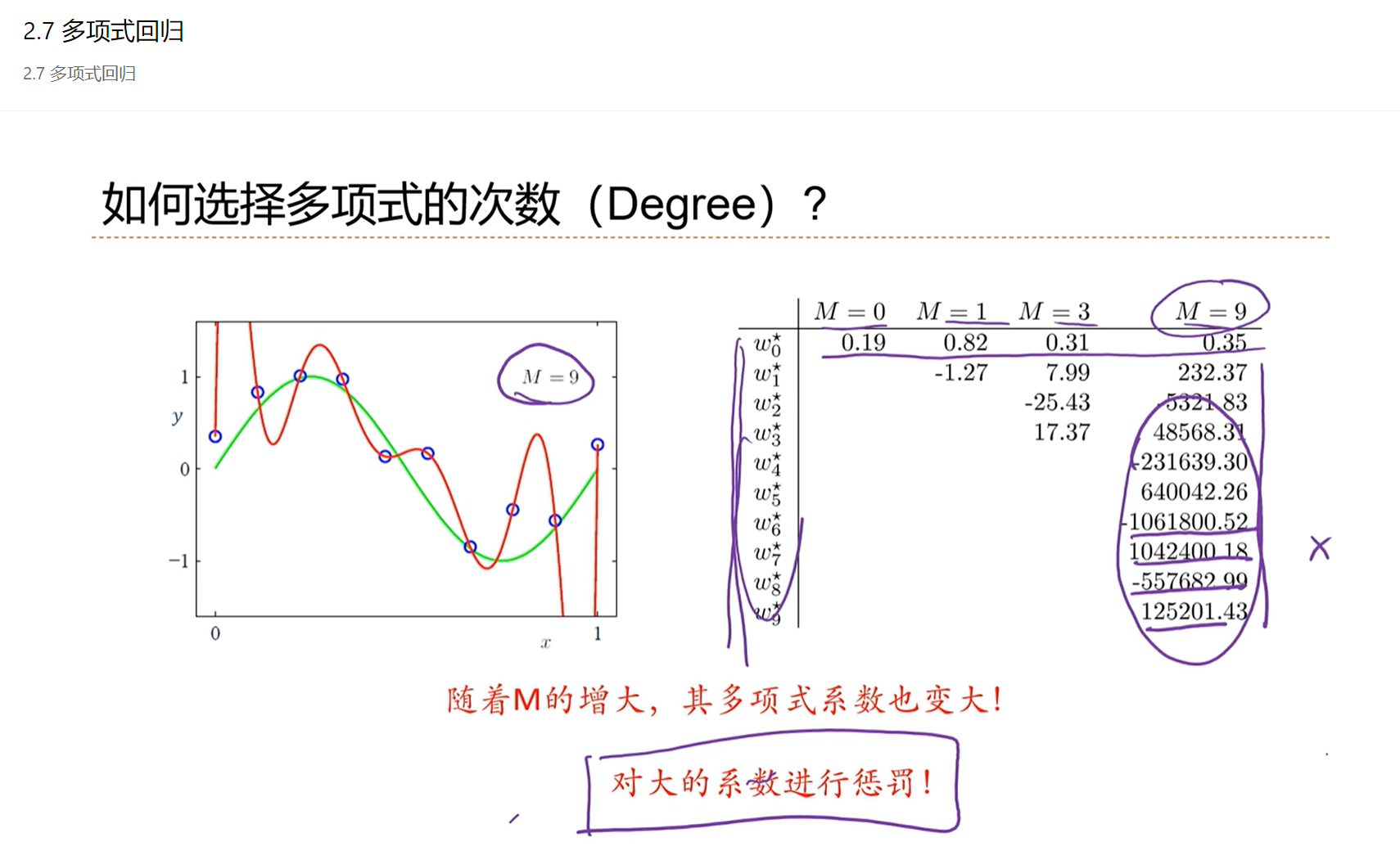

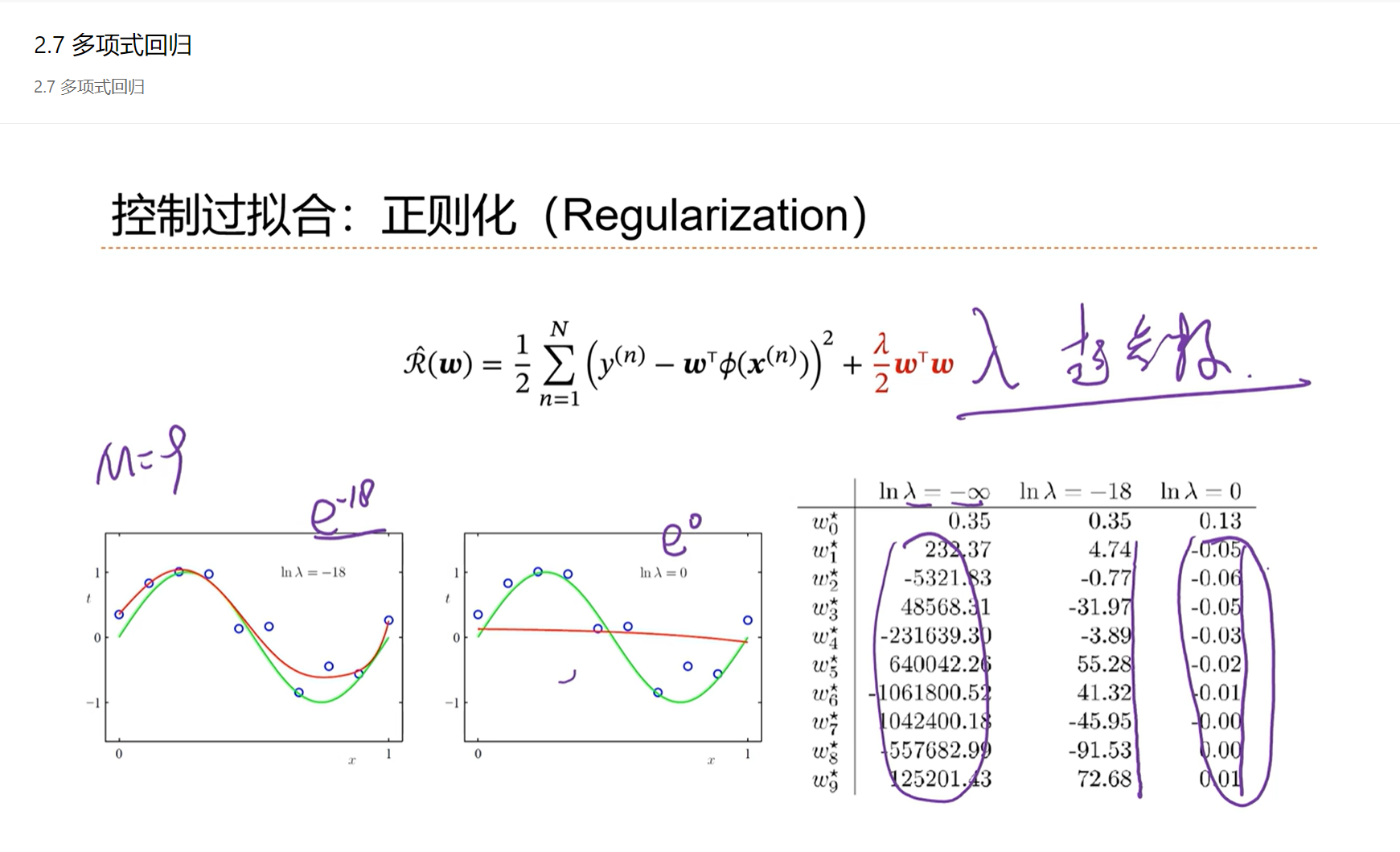
防止模型过拟合的方法,除了增加正则化之外,最简单的办法就是增加训练样本的数量。
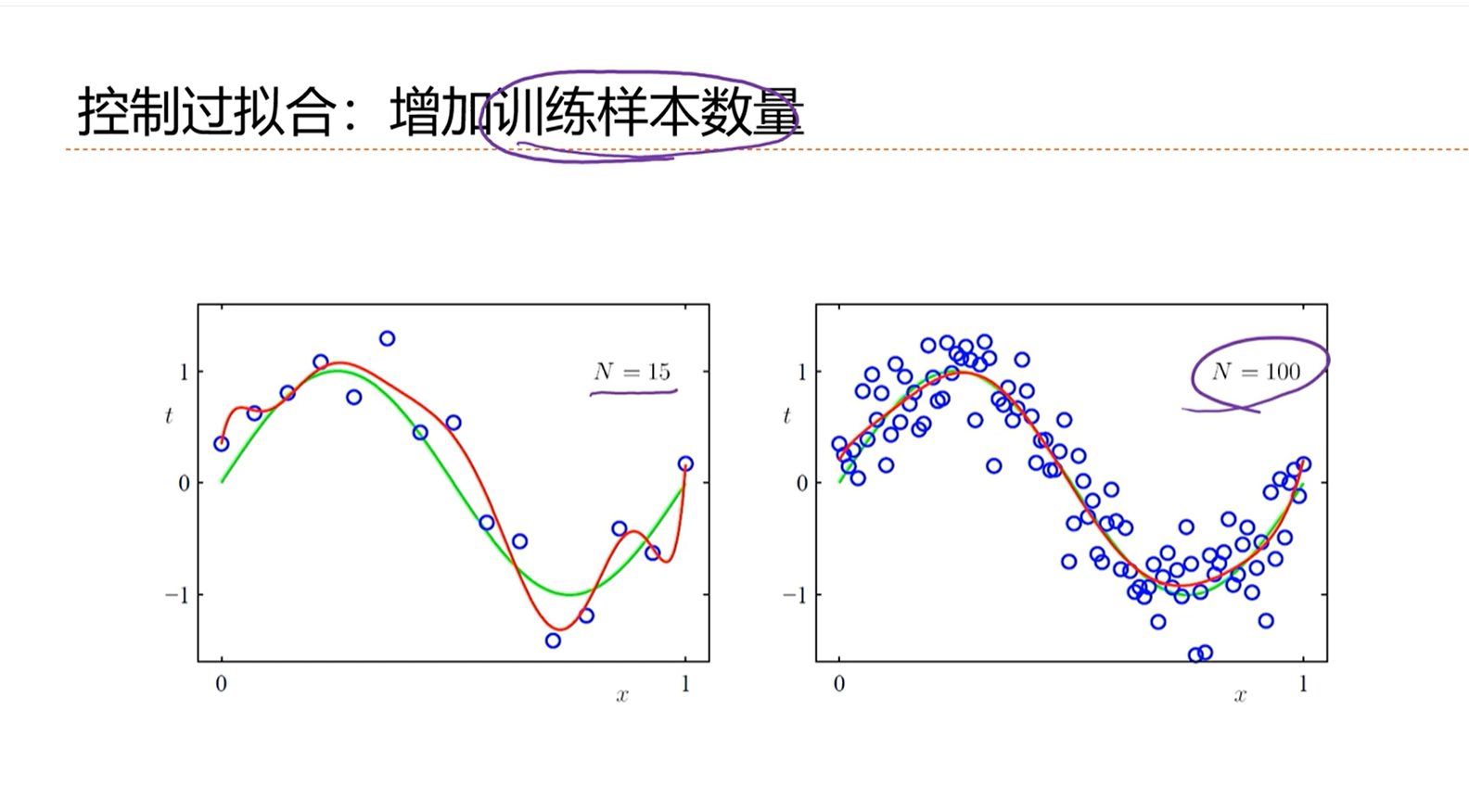
当样本数量N非常大的时候,经验风险就趋向于期望风险。
2.8 - 线性回归的概率视角
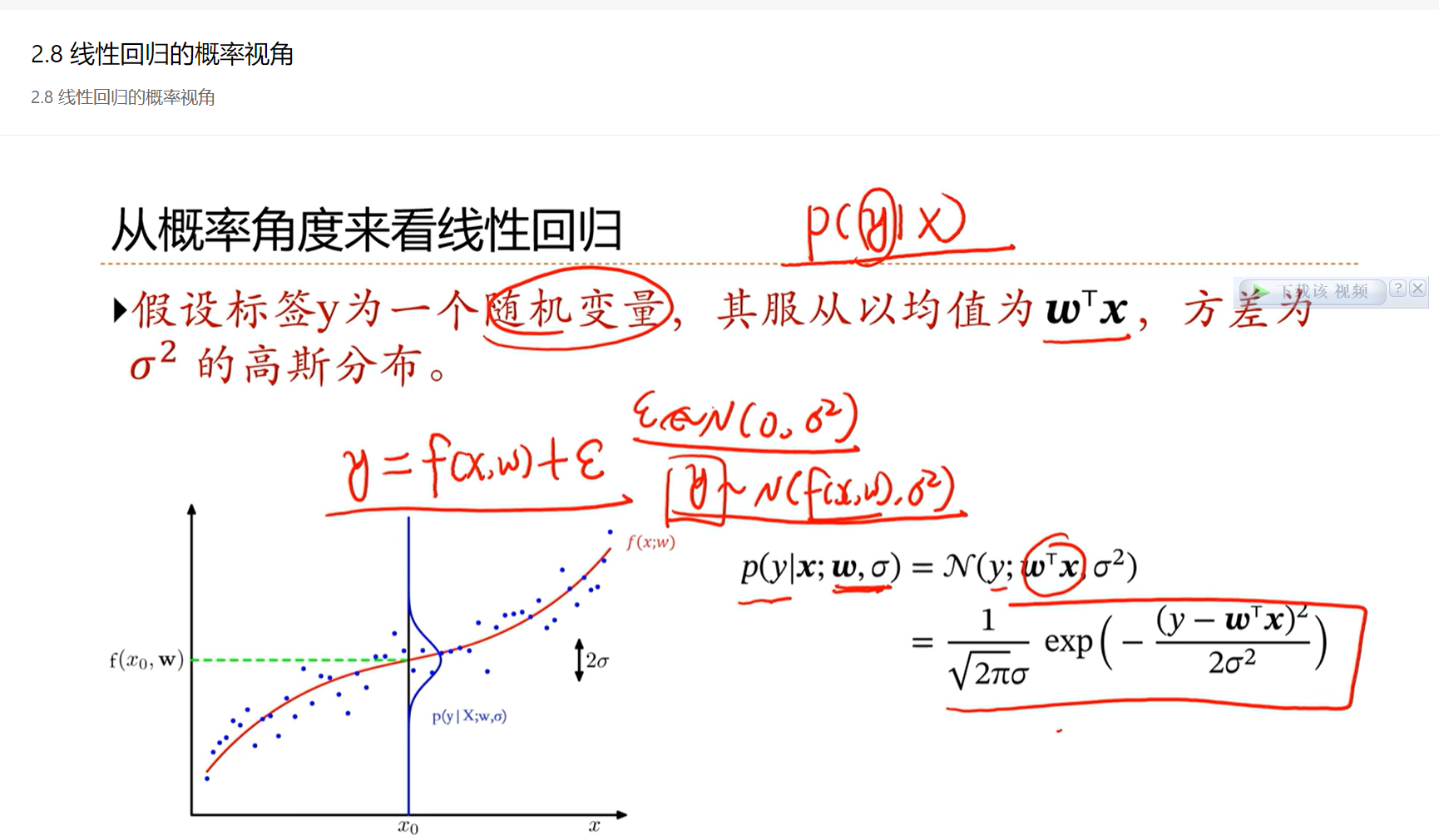







最大后验估计和结构风险最小化是非常相似的
2.9 - 模型选择与”偏差-方差”分解

如何选择模型:引入验证集帮助选择模型,选择在验证集上错误最小的模型

==使用验证集存在的问题:==
由于本来数据就少,还要拿出一部分作为验证集,就会导致训练数据更加的稀疏。
解决方法是交叉验证的方法。

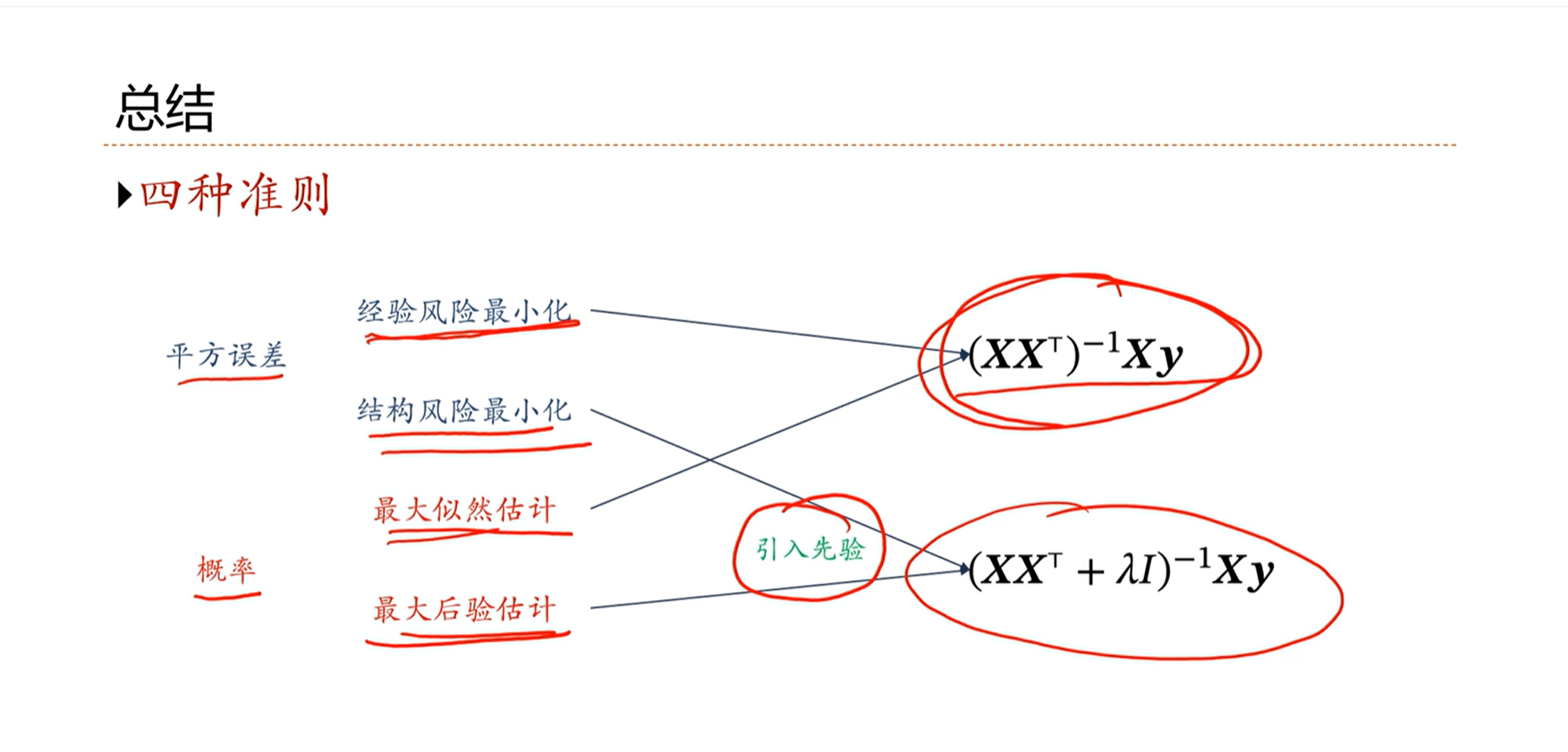
除了在验证集的指导下选择模型,还可以在一些准则的指导下选择模型。




1)偏差:在不同的数据集学习到的模型的平均值和最优模型之间的差
2)方差:在不同的数据集学习到的模型之间的差值
3)机器学习模型无法避免的错误
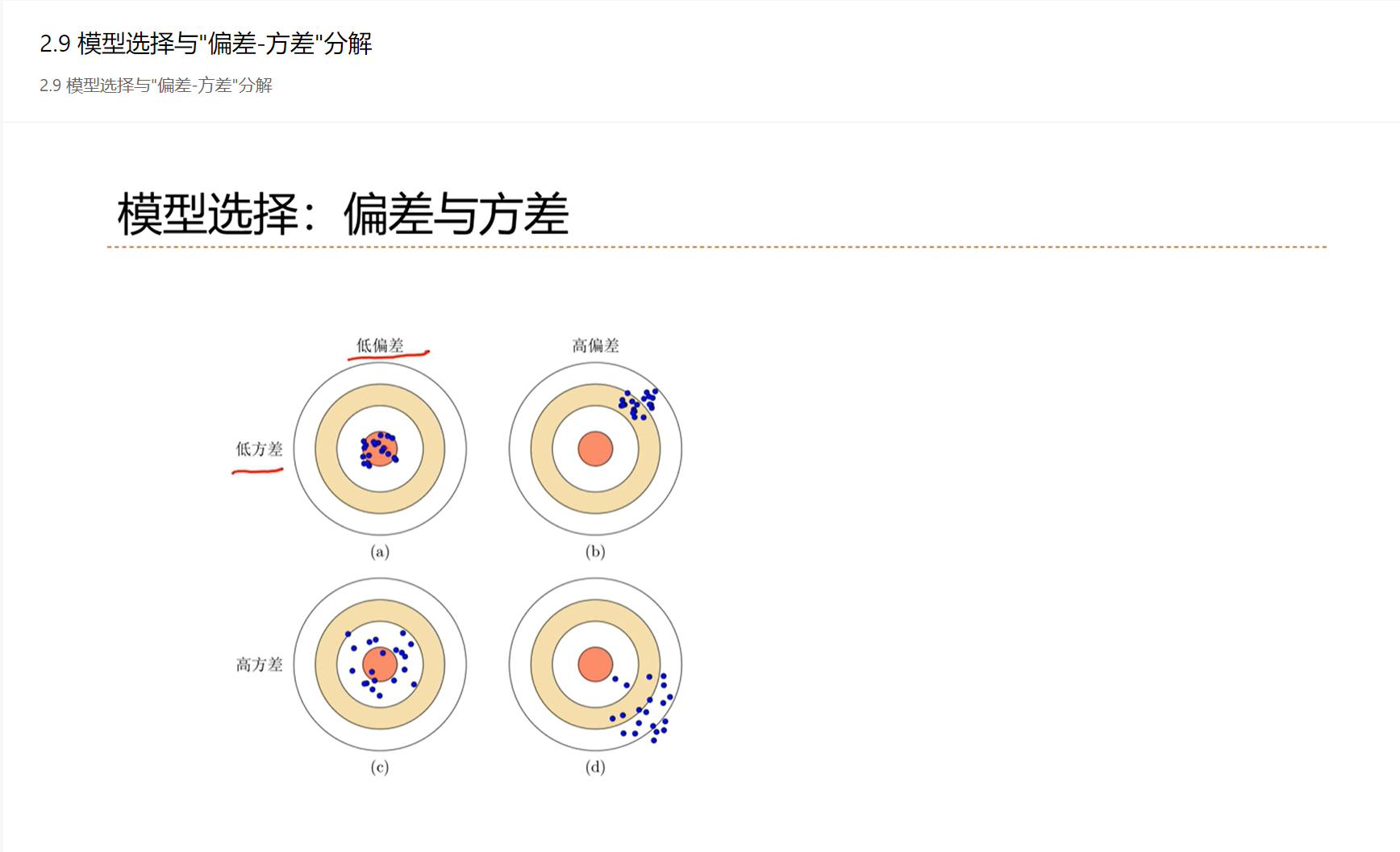
低方差、低偏差:理想、最优
低方差、高偏差:通常是模型能力不够,欠拟合
低偏差、高方差:模型能力是可以的,但是能力过高、过拟合
高偏差、高方差:尽可能的避免
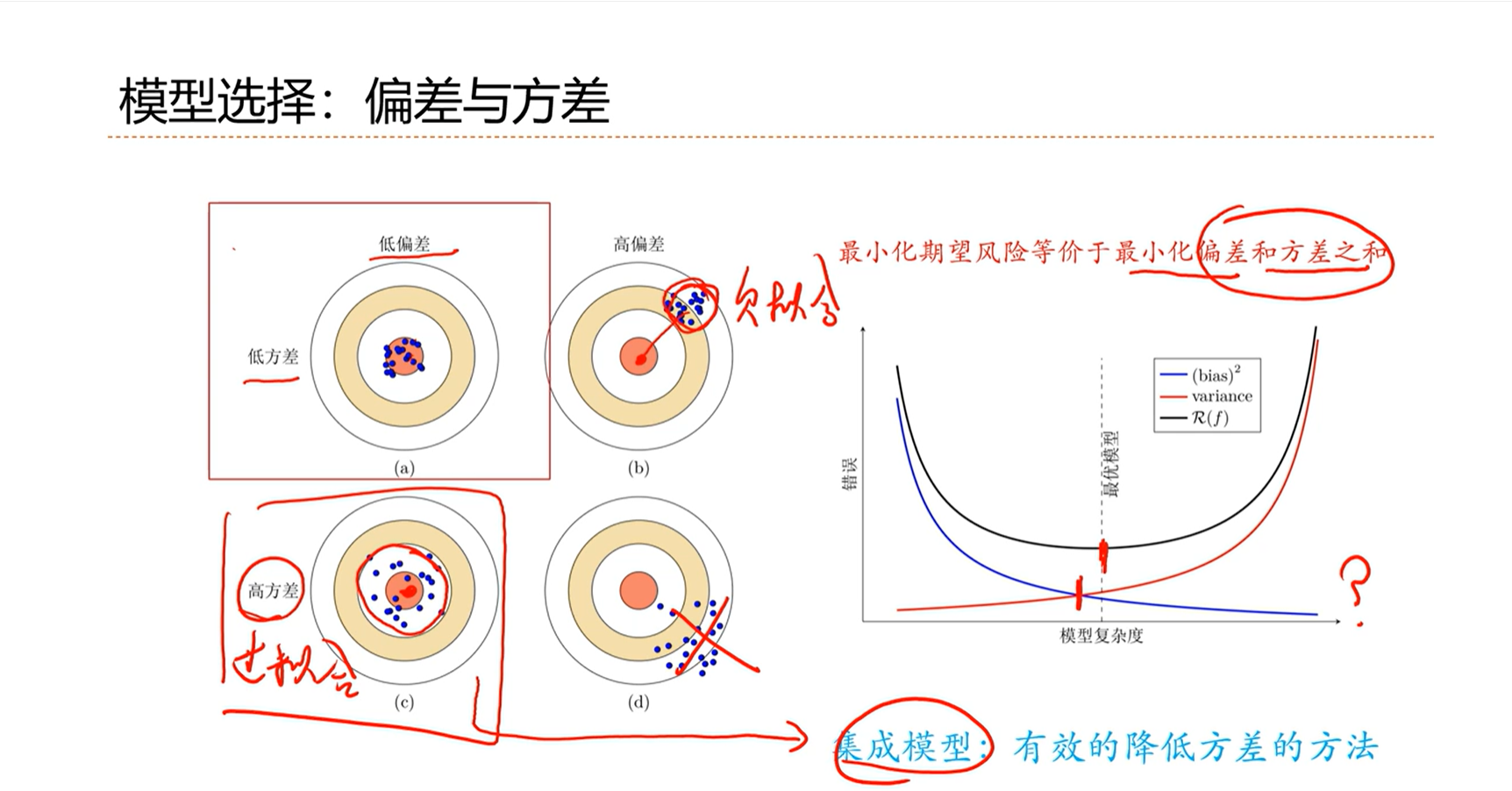
通常来讲,随着模型复杂度的增加,模型的偏差是在不断地减小、方差是在不断的增加。即完成了任务、但是开始躁动、不稳定了。
最优的模型不一定是处于偏差线和方差线之间的交点上。
随着模型能力的提高,开始过拟合,即低偏差、高方差。
解决低偏差、高方差问题的一个手段是集成模型。即将在不同的数据集上训练出来的模型做一个平均。