008 - 文章阅读笔记：混合密度网络：也许你需要的是一颗骰子 - 知乎 - esang

本文最后更新于：3 个月前

参考文章：

混合密度网络：也许你需要的是一颗骰子 - 知乎 - esang

编辑于 2021-04-16 19:14

ps：本文为依据个人日常阅读习惯，在原文的基础上记录阅读进度、记录个人想法和收获所写，关于原文一切内容的著作权全部归原作者所有。

混合密度网络：也许你需要的是一颗骰子

Kaggle上的”Jane Street Market Predictio“竞赛已经告一段落，部分高位选手的方案也陆续公开，骚操作也是层出不穷。今天介绍一个第二名选手使用的混合密度网络(Mixture Density Networks)，原帖在：

Jane Street Market Predictionwww.kaggle.com/c/jane-street-market-prediction/discussion/226837

基于通用近似定理，神经网络可以近似任意函数，但有一个潜在的问题，那就是神经网络拟合的比较好的是单峰分布，对多峰分布的拟合能力堪忧。简单来说，就是当一个x对应一个t值的时候，神经网络表现不错，但是当一个x对应多个t的时候就很拉跨了。

alec：

  • dice = 骰子

因为从概率的角度，神经网络是在拟合p(t|x)的分布，但在一些随机性或者波动性比较大的环境中，比如股价未来的走势可能是一个分布，而非一个确定的数值。所以在难以做出精确决策，无法得知骰子究竟掷到几的时候，知道骰子每个面的胜率也是非常有价值的。而混合密度网络就是一个去拟合骰子本身的神经网络。

那么问题来了，让神经网络去拟合一个值很好理解，用均方误差不断优化就行了。但去拟合一个分布，就有两个问题：一是如何让神经网络可以表示一个任意的分布，二是用什么样的损失函数训练这个网络。

alec：

  • GMM = 高斯混合模型 = gauss mix model
  • M = mid = 混合

第一个问题高斯混合模型（GMM）已经给出了答案：「理论上，多个高斯分布的加权和可以近似任意条件概率分布。」 （这种近似其实是有条件的，但是一般情况下可以无视）

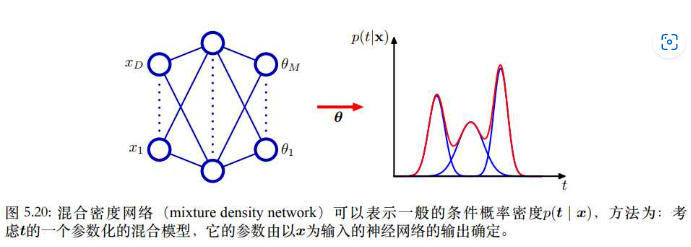
即分布P(t|x)可以表示成K个高斯分布的加权和，第K个高斯分布的权重为πk(x)，均值为μk(x), 方差为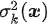image-20230207183852928：

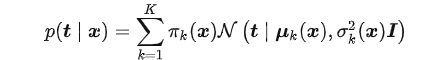
image-20230207183931411

所以我们只需要用三个神经网络分别来拟合这K个分布的权重、均值和方差。当然，因为权重和方差有一些限制：权重要保证和为1，所以使用一个softmax激活函数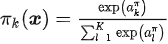image-20230207184059446；方差要保证不为负，所以使用一个指数函数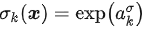image-20230207184111764

image-20230207184231856

alec：

  • 神经网络难以表示非确定性的公式。混合密度网络（MDN），可以用来表示一个条件概率密度。

对于第二个问题，如何设计损失函数。既然我们得到的是一个概率分布，那么按照极大似然估计的原则，这个概率分布应该让我们观测到样本的概率尽可能大。也就是让这个混合概率分布中t的概率尽可能大：

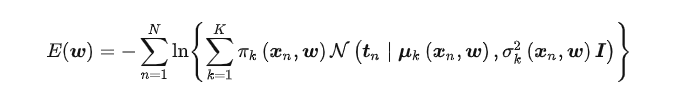
image-20230207192219913

当然，这只是比较原始的混合密度网络，后续出现了一些改进，这里给一个竞赛中的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# 代码来自于：https://www.kaggle.com/c/jane-street-market-prediction/discussion/226837
class MDNDecisionMaker(nn.Module):
    def __init__(self, in_dim, out_dim, hidden_dim, dropout_prob):
        super().__init__()
        self.hidden = hidden_dim
        self.out_dim = out_dim
        self.dropout = dropout_prob
        self.feed_forward_network = nn.Sequential(
            nn.BatchNorm1d(in_dim),
            nn.Linear(in_dim, self.hidden), #1
            nn.SiLU(),
            nn.Dropout(p = 0.3),
            nn.Linear(self.hidden, self.hidden), #2
            nn.SiLU(),
            nn.Dropout(p = 0.3),
            nn.Linear(self.hidden, self.hidden), #3
            nn.SiLU(),
            nn.Dropout(p = 0.3),
            nn.Linear(self.hidden, self.hidden), #3
            nn.SiLU(),
            nn.BatchNorm1d(self.hidden)
        ).double()
        # predict mean value of multivariate gaussian distribution
        self.mean_network = nn.Sequential(
            nn.Linear(self.hidden, self.hidden), #3
            nn.SiLU(),
            nn.Linear(self.hidden, out_dim)
        ).double()
        # predict non diagonal lower triangular values of matrix
        self.cholesky_nondiag_sigmas_network = nn.Sequential(
            nn.Linear(self.hidden, self.hidden), #3
            nn.SiLU(),
            nn.Linear(self.hidden, out_dim*out_dim), #2
        ).double()
        # predict the diagonal elements, these must be non zero to ensure invertibility
        self.cholesky_diag_sigmas_network = nn.Sequential(
            nn.Linear(self.hidden, self.hidden), #3
            nn.SiLU(),
            nn.Linear(self.hidden, out_dim)
        ).double()
        self.bceloss = nn.BCELoss()

    def forward(self, x, return_covariance = False):
        parameters = self.feed_forward_network(x.double())
        means = self.mean_network(parameters)
        cholesky_lower_triangular = torch.tril(self.cholesky_nondiag_sigmas_network(parameters).view(-1, self.out_dim, self.out_dim), diagonal = -1)
        cholesky_diag = torch.diag_embed(torch.exp(self.cholesky_diag_sigmas_network(parameters)).view(-1, self.out_dim))
        cholesky_sigmas =  cholesky_diag + cholesky_lower_triangular
        if return_covariance:
            covariances = torch.bmm(cholesky_sigmas, torch.transpose(cholesky_sigmas, 1, 2))
            return mean, covariances
        return means, cholesky_sigmas