009 - 文章阅读笔记:混合密度网络(MDN)进行多元回归详解和代码示例 - 数据派THU(清华大学数据软件团队官方微信公众号)
本文最后更新于:3 个月前
原文链接:
混合密度网络(MDN)进行多元回归详解和代码示例 - 数据派THU(清华大学数据软件团队官方微信公众号)
2022-03-08 17:00
ps:本文为依据个人日常阅读习惯,在原文的基础上记录阅读进度、记录个人想法和收获所写,关于原文一切内容的著作权全部归原作者所有。
[√] 文章信息

来源:Deephub Imba
本文约4900字,建议阅读5分钟
在本文中,首先简要解释一下 混合密度网络 MDN (Mixture Density Network)是什么,然后将使用Python 代码构建 MDN 模型,最后使用构建好的模型进行多元回归并测试效果。
[√] 回归
“回归预测建模是逼近从输入变量 (X) 到连续输出变量 (y) 的映射函数 (f) […] 回归问题需要预测具体的数值。具有多个输入变量的问题通常被称为多元回归问题 例如,预测房屋价值,可能在 100,000 美元到 200,000 美元之间
这是另一个区分分类问题和回归问题的视觉解释如下:
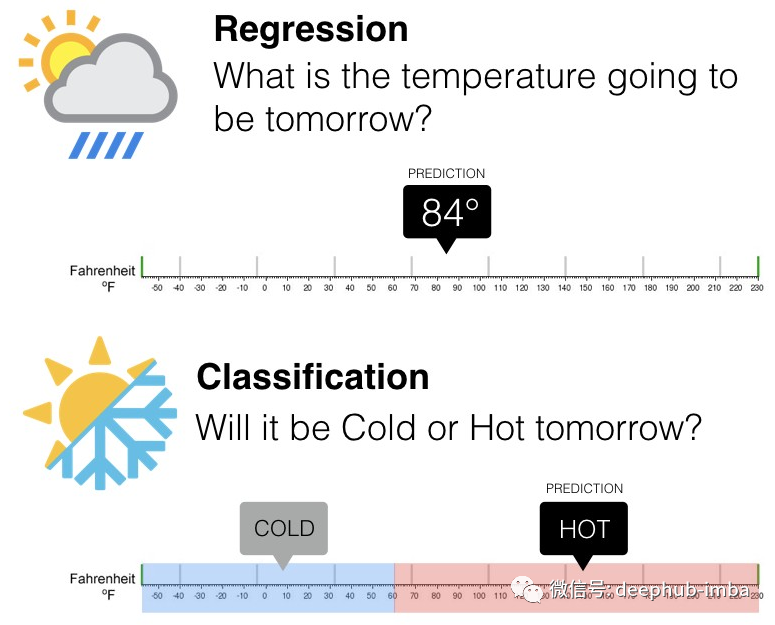
另外一个例子
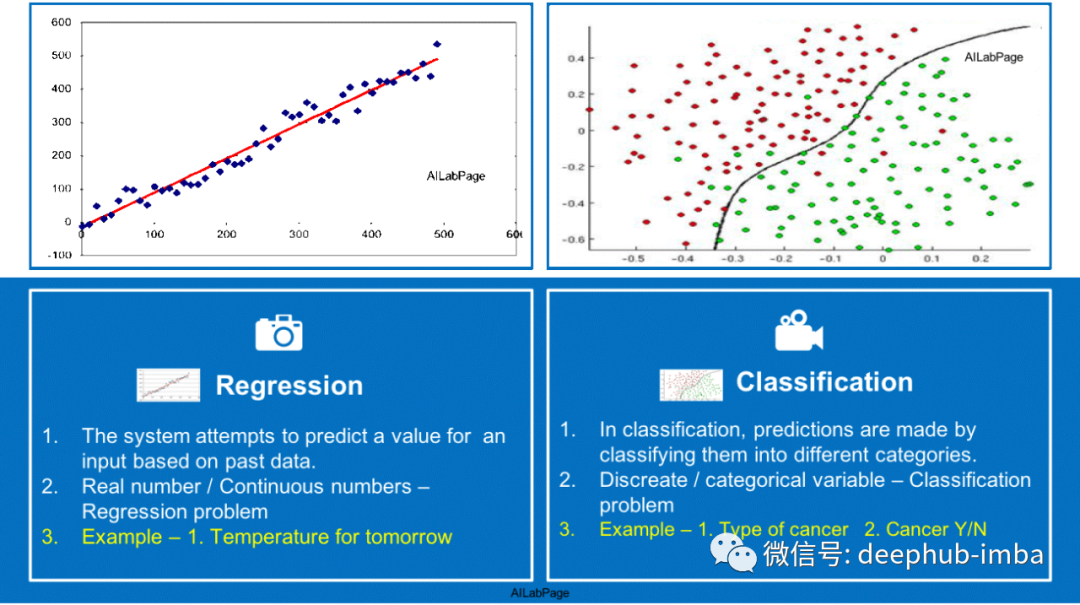
alec:
- 分类问题是预测类别
- 回归问题是预测模型(公式)
[√] 密度
DENSITY “密度” 是什么意思?这是一个快速的通俗示例:
假设正在为必胜客运送比萨。现在记录刚刚进行的每次交付的时间(以分钟为单位)。交付 1000 次后,将数据可视化以查看工作表现如何。这是结果:
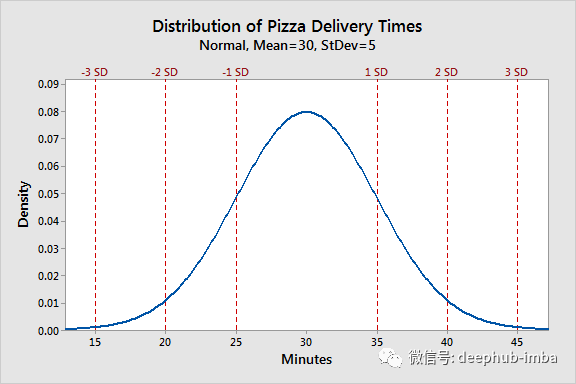
这是披萨交付时间数据分布的“密度”。平均而言,每次交付需要 30 分钟(图中的峰值)。它还表示,在 95% 的情况下(2 个标准差2sd ),交付需要 20 到 40 分钟才能完成。密度种类代表时间结果的“频率”。“频率”和“密度”的区别在于:
- 频率:如果你在这条曲线下绘制一个直方图并对所有的 bin 进行计数,它将求和为任何整数(取决于数据集中捕获的观察总数)。
- 密度:如果你在这条曲线下绘制一个直方图并计算所有的 bin,它总和为 1。我们也可以将此曲线称为概率密度函数 (pdf)。
- 用统计术语来说,这是一个漂亮的正态/高斯分布。这个正态分布有两个参数:
[√] 均值
- 标准差:“标准差是一个数字,用于说明一组测量值如何从平均值(平均值)或预期值中展开。低标准偏差意味着大多数数字接近平均值。高标准差意味着数字更加分散。“
均值和标准差的变化会影响分布的形状。例如:
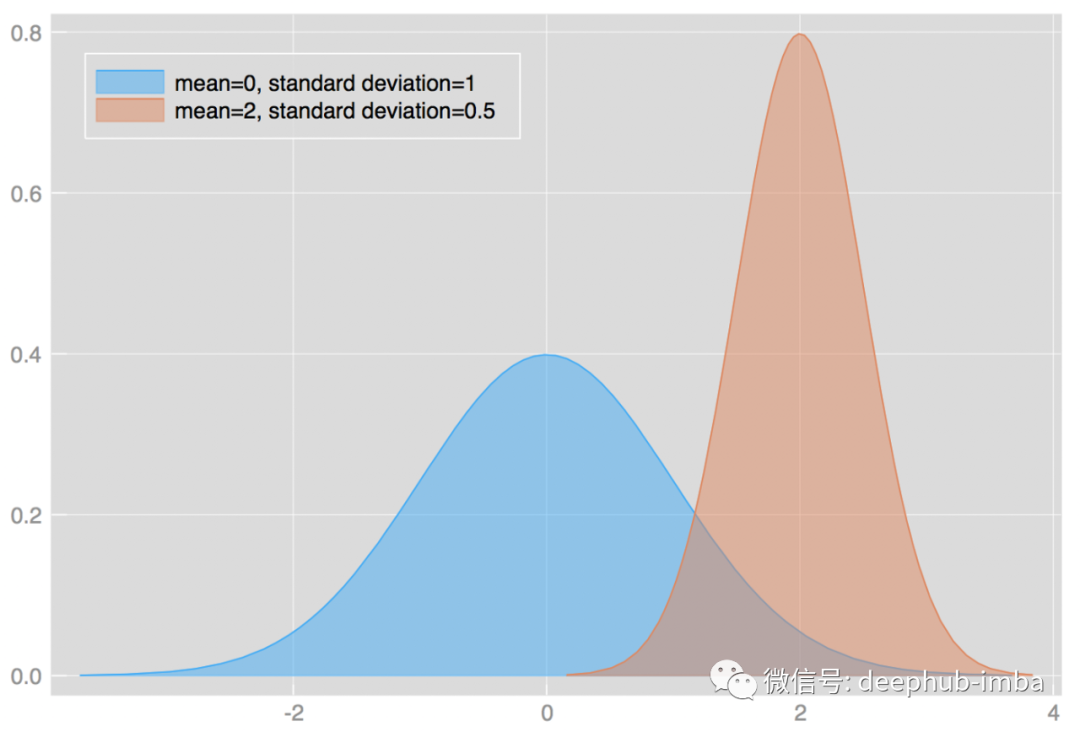
alec:
- 标准差和方差越大,数字越分散。
有许多具有不同类型参数的各种不同分布类型。例如:
[√] 混合密度
现在让我们看看这 3 个分布:
如果我们采用这种双峰分布(也称为一般分布):
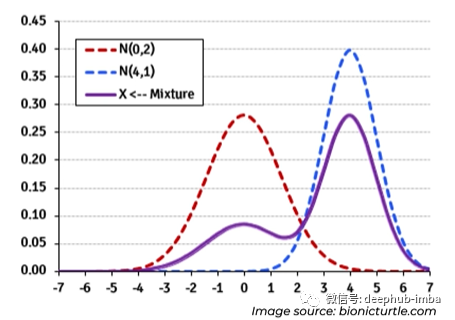
混合密度网络使用这样的假设,即任何像这种双峰分布的一般分布都可以分解为正态分布的混合(该混合也可以与其他类型的分布一起定制 例如拉普拉斯):
alec:
- 混合密度网络的假设:任何的多峰分布,能够分解为正态分布的混合。
[√] 网络架构
混合密度网络也是一种人工神经网络。这是神经网络的经典示例:
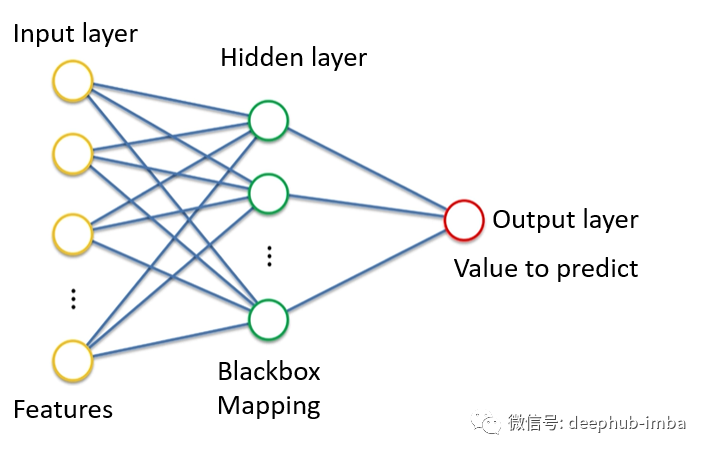
输入层(黄色)、隐藏层(绿色)和输出层(红色)。
如果我们将神经网络的目标定义为学习在给定一些输入特征的情况下输出连续值。在上面的例子中,给定年龄、性别、教育程度和其他特征,那么神经网络就可以进行回归的运算。
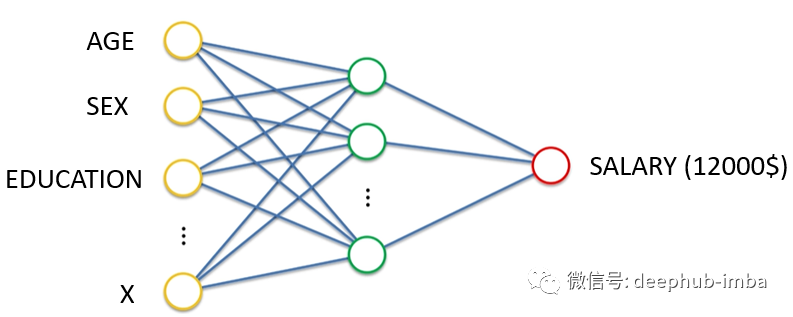
alec:
- 回归是预测一个输出值,分类是预测一个分类。输出值有无数个,分类有N个。回归的输出是连续的,分类的输出是有限且离散的。
[√] 密度网络
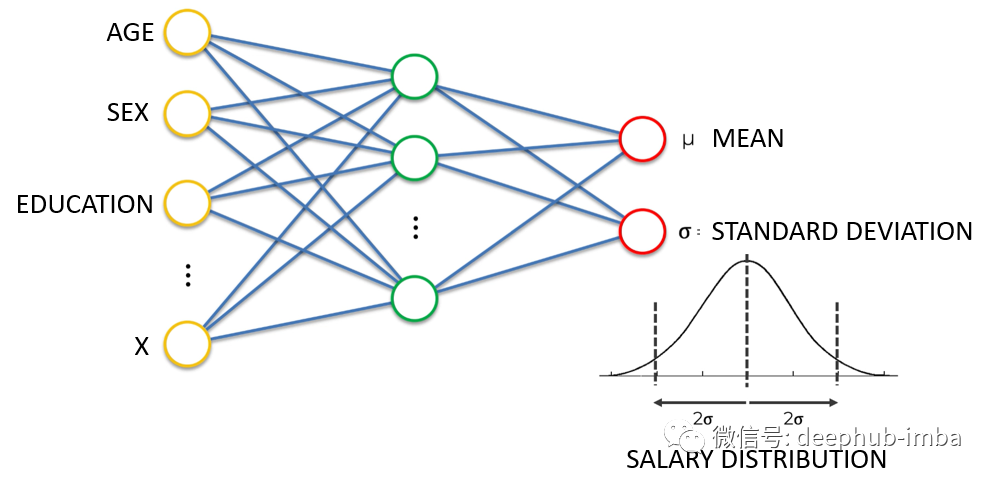
- 密度网络也是神经网络,其目标不是简单地学习输出单个连续值,而是学习在给定一些输入特征的情况下输出分布参数(此处为均值和标准差)。
- 在上面的例子中,给定年龄、性别、教育程度等特征,神经网络学习预测期望工资分布的均值和标准差。预测分布比预测单个值具有很多的优势,例如能够给出预测的不确定性边界。
- 这是解决回归问题的“贝叶斯”方法。下面是预测每个预期连续值的分布的一个很好的例子:
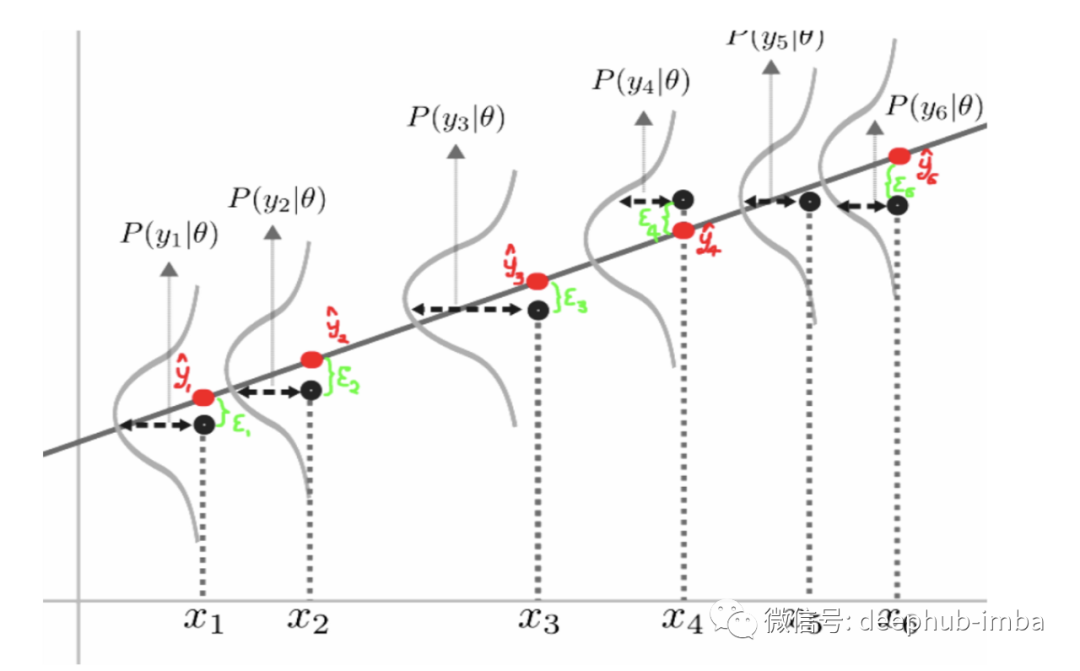
下面的图片向我们展示了每个预测实例的预期值分布:
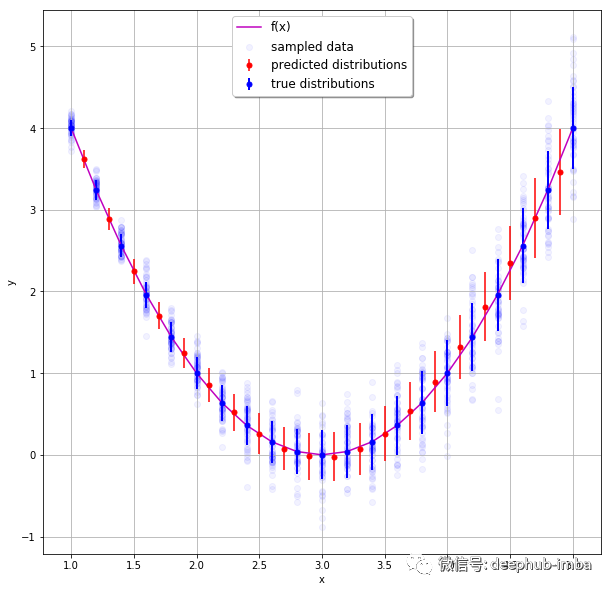
alec:
- 密度网络属于神经网络,但是不同于一般的神经网络简单的学习输出单个连续值。而是学习在给定一些输入特征的情况下的输出分布参数(此处为均值和标准差)。
[√] 混合密度网络
最后回到正题,混合密度网络的目标是在给定特定输入特征的情况下,学习输出混合在一般分布中的所有分布的参数(此处为均值、标准差和 Pi)。新参数“Pi”是混合参数,它给出最终混合中给定分布的权重/概率。
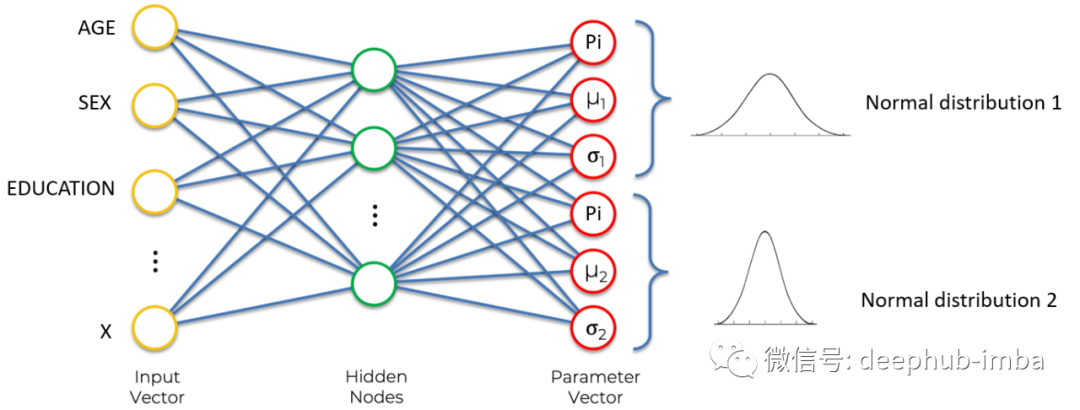
最终结果如下:

alec:
- 最后回到正题,混合密度网络的目标是在给定特定输入特征的情况下,学习输出混合在一般分布中的所有分布的参数(此处为均值、标准差和 Pi)。新参数“Pi”是混合参数,它给出最终混合中给定分布的权重/概率。
[√] 示例1:单变量数据的 MDN 类
上面的定义和理论基础已经介绍完毕,下面我们开始代码的演示:
1 | |
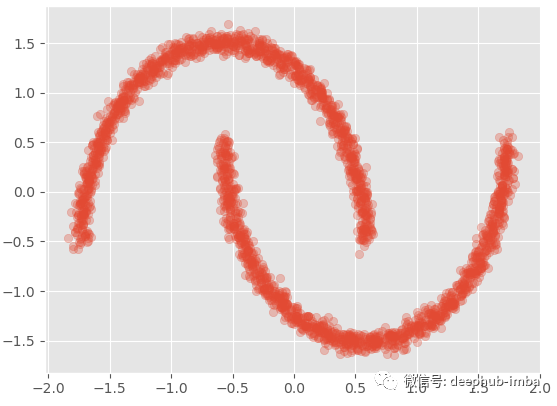
生成著名的“半月”型的数据集:
1 | |
绘制目标值 (y) 的密度分布:
1 | |
通过查看数据,我们可以看到有两个重叠的簇:
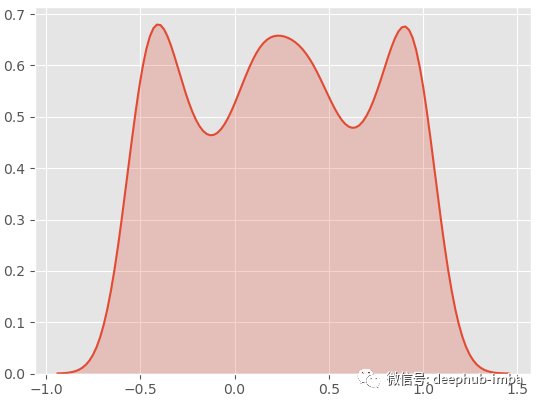
这时一个很好的多模态分布(一般分布)。如果我们在这个数据集上尝试一个标准的线性回归来用 X 预测 y:
1 | |
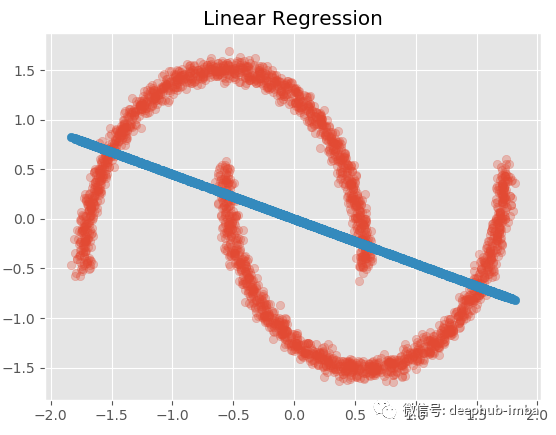
1 | |
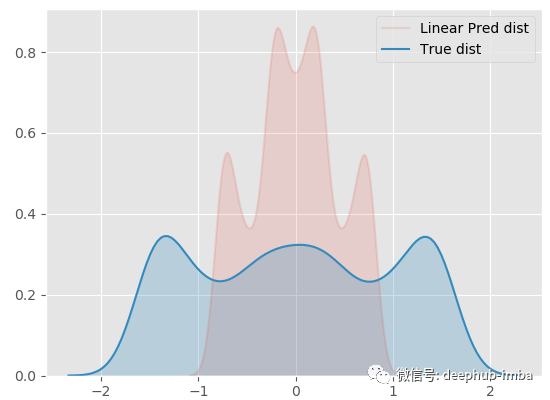
效果必须不好!现在让尝试一个非线性模型(径向基函数核岭回归):
1 | |
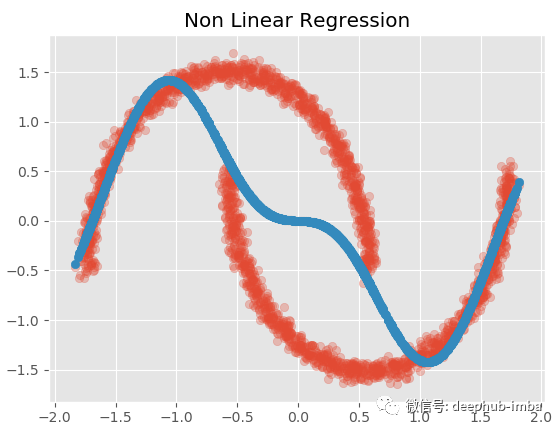
1 | |
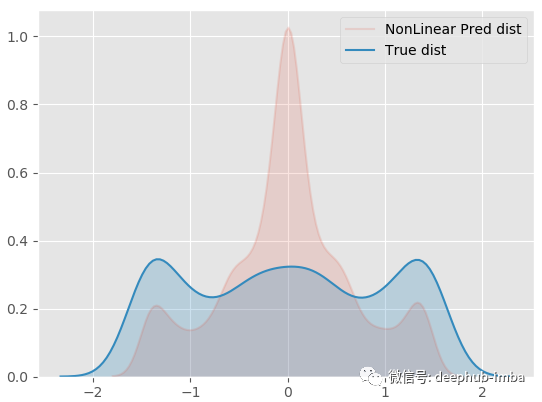
虽然结果也不尽如人意,但是比上面的线性回归要好很多了。
两个模型都没有成功的主要原因是:对于同一个 X 值存在多个不同的 y 值……更具体地说,对于同一个 X 似乎存在不止一个可能的 y 分布。回归模型只是试图找到最小化误差的最优函数,并没有考虑到密度的混合,所以 中间的那些X没有唯一的Y解,它们有两种可能的解,所以导致了以上的问题。
现在让我们尝试一个 MDN 模型,这里已经实现了一个快速且易于使用的“fit-predict”、“sklearn alike”自定义 python MDN 类。如果您想自己使用它,这是 python 代码的链接(请注意:这个 MDN 类是实验性的,尚未经过广泛测试):https://github.com/CoteDave/blog/blob/master/Made%20easy/MDN%20regression/mdn_model.py
为了能够使用这个类,有 sklearn、tensorflow probability、Tensorflow < 2、umap 和 hdbscan(用于自定义可视化类 功能)。
1 | |
alec:
- nerve,神经
- neuron,神经元
类的参数总结如下:
- n_mixtures:MDN 使用的分布混合数。如果设置为 -1,它将使用高斯混合模型 (GMM) 和 X 和 y 上的 HDBSCAN 模型“自动”找到最佳混合数。
- dist:在混合中使用的分布类型。目前,有两种选择;“正常”或“拉普拉斯”。(基于一些实验,拉普拉斯分布比正态分布更好的结果)。
- input_neurons:在MDN的输入层中使用的神经元数量
- hidden_neurons:MDN的 隐藏层架构。每个隐藏层的神经元列表。此参数使您能够选择隐藏层的数量和每个隐藏层的神经元数量。
- gmm_boost:布尔值。如果设置为 True,将向数据集添加簇特征。
- optimizer:要使用的优化算法。
- learning_rate:优化算法的学习率
- early_stopping:避免训练时过拟合。当指标在给定数量的时期内没有变化时,此触发器将决定何时停止训练。
- tf_mixture_family:布尔值。如果设置为 True,将使用 tf_mixture 系列(推荐):Mixture 对象实现批量混合分布。
- input_activation:输入层的激活函数
- hidden_activation:隐藏层的激活函数
现在 MDN 模型已经拟合了数据,从混合密度分布中采样并绘制概率密度函数:
1 | |
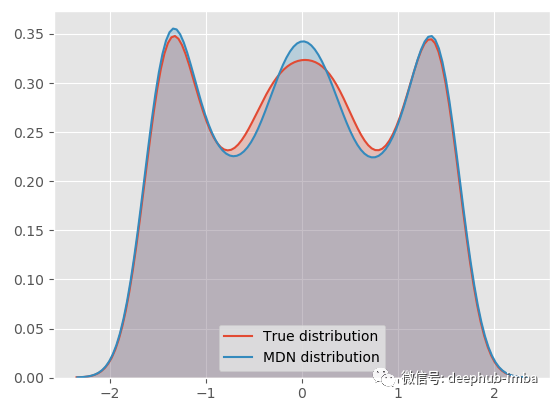
我们的 MDN 模型非常适合真正的一般分布!下面将最终的混合分布分解为每个分布,看看它的样子:
1 | |
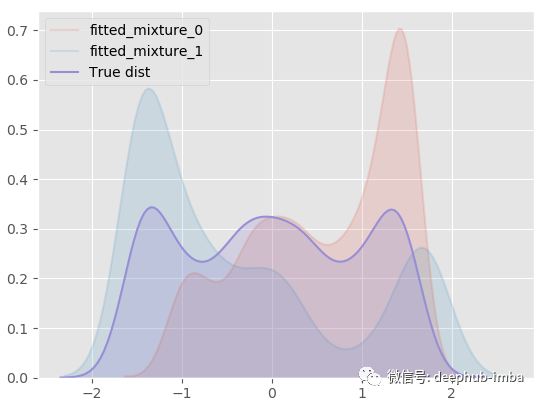
使用学习到的混合分布再次采样一些 Y 数据,生成的样本与真实样本进行对比:
1 | |
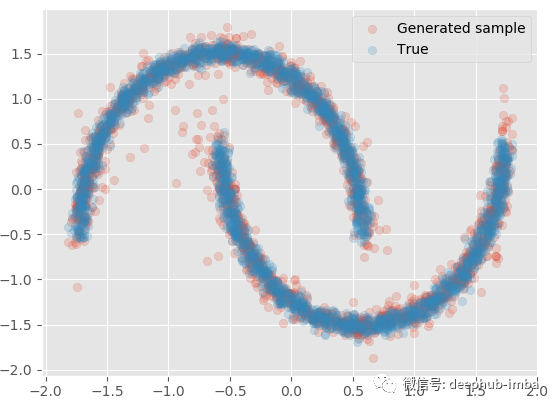
与实际的数据非常接近,如果,给定 X还可以生成多批样本以生成分位数、均值等统计信息:
1 | |
绘制每个学习分布的平均值,以及它们各自的混合权重 (pi):
1 | |
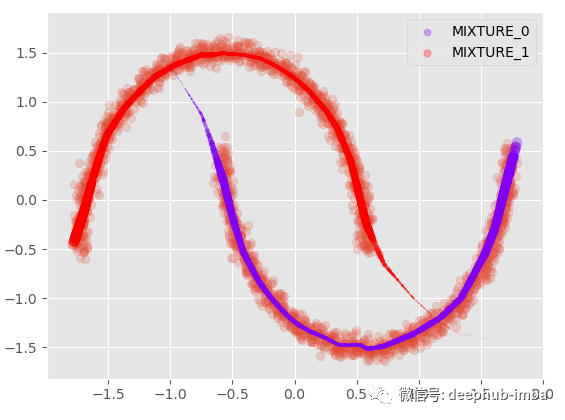
有每个分布的均值和标准差,还可以绘制带有完整不确定性;假设我们以 95% 的置信区间绘制平均值:
1 | |
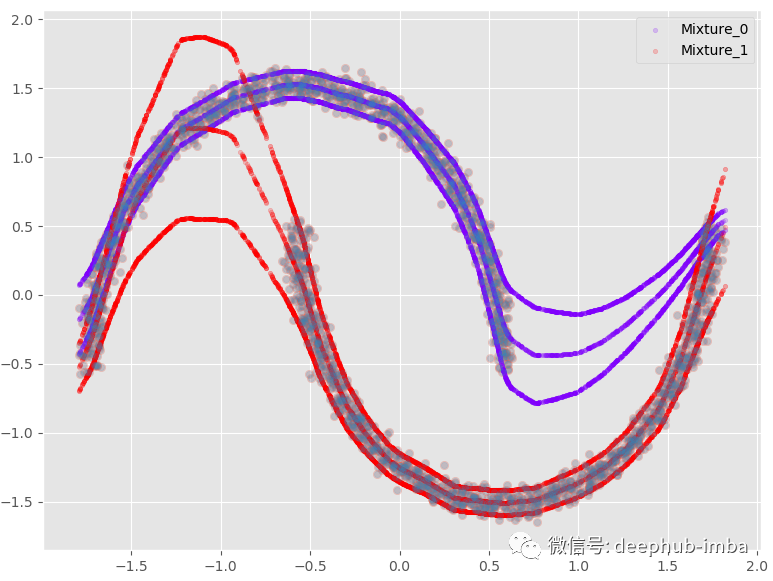
将分布混合在一起,当对同一个 X 有多个 y 分布时,我们使用最高 Pi 参数值选择最可能的混合:
Y_preds = 对于每个 X,选择具有最大概率/权重(Pi 参数)的分布的 Y 均值
1 | |
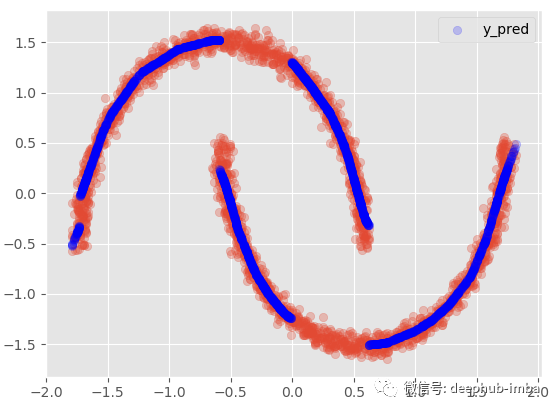
这种方式表现得并不理想,因为在数据中显然有两个不同的簇重叠,密度几乎相等。使得误差将高于标准回归模型。这也意味着数据集中可能缺少一个可以帮助避免集群在更高维度上重叠重要特征。
我们还可以选择使用 Pi 参数和所有分布的均值混合分布:
· Y_preds = (mean_1 * Pi1) + (mean_2 * Pi2)
1 | |
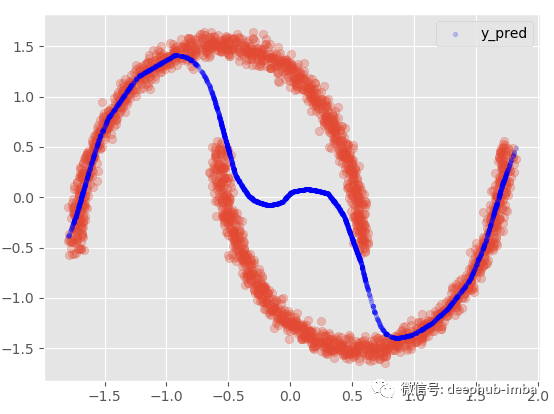
如果我们添加 95 置信区间:
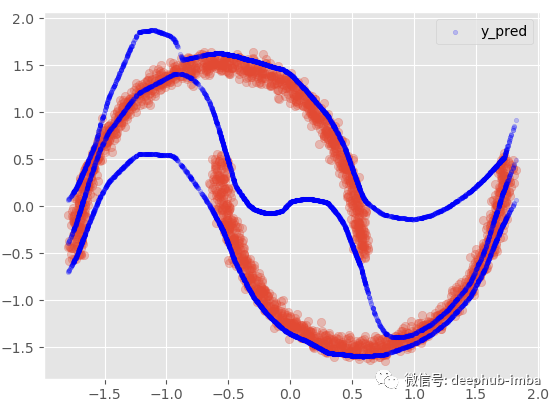
这个选项提供了与非线性回归模型几乎相同的结果,混合所有内容以最小化点和函数之间的距离。在这个非常特殊的情况下,我最喜欢的选择是假设在数据的某些区域,X 有多个 Y,而在其他区域;仅使用其中一种混合。:
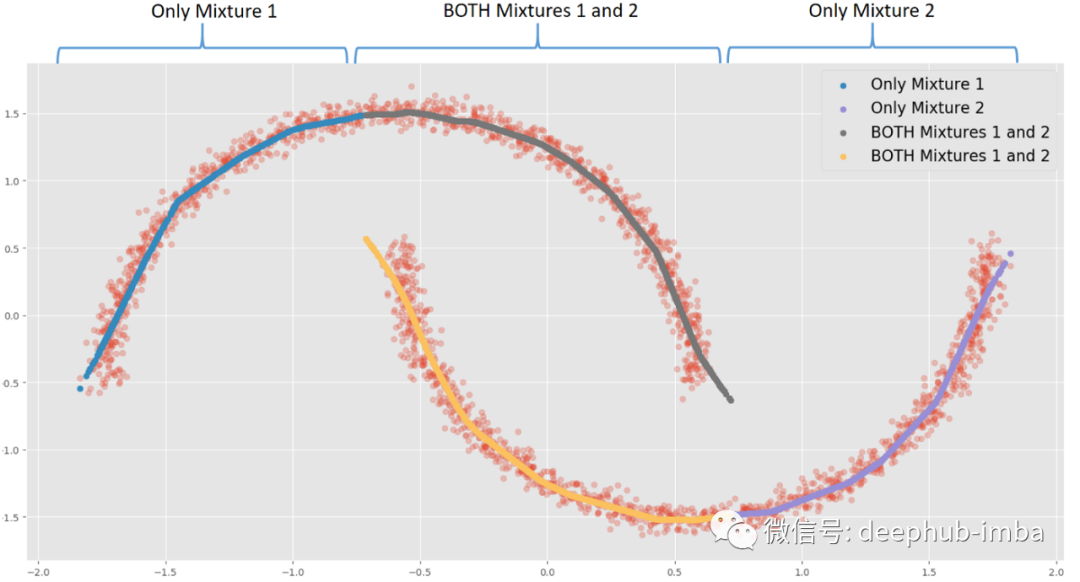
例如,当 X = 0 时,每种混合可能有两种不同的 Y 解。当 X = -1.5 时,混合 1 中存在唯一的 Y 解决方案。根据用例或业务上下文,当同一个 X 存在多个解决方案时,可以触发操作或决策。
这个选项得含义是当存在重叠分布时(如果两个混合概率都 >= 给定概率阈值),行将被复制:
1 | |
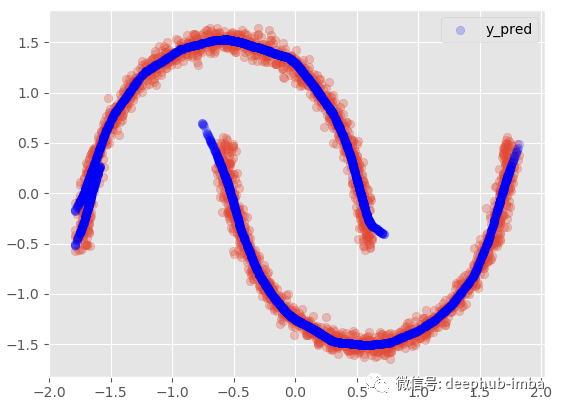
使用 95% 置信区间:
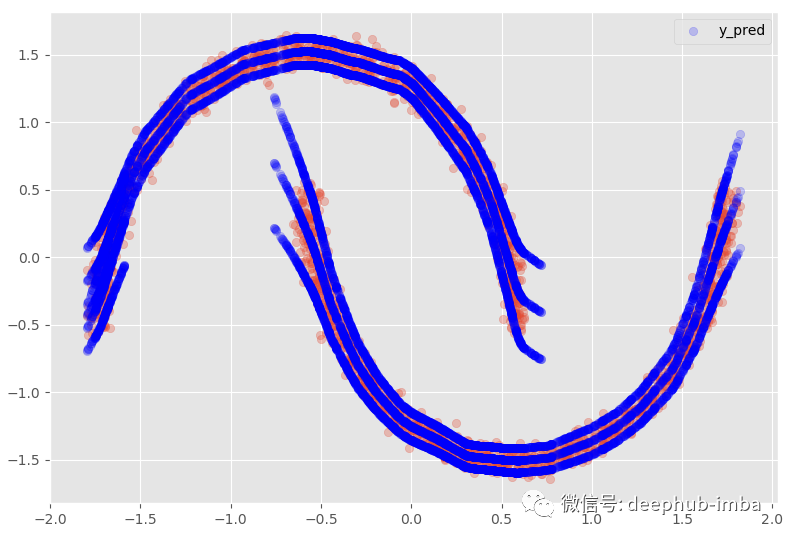
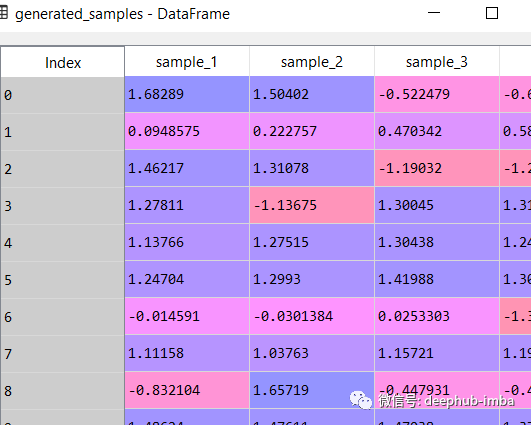
数据集行从 2500 增加到了 4063,最终预测数据集如下所示:
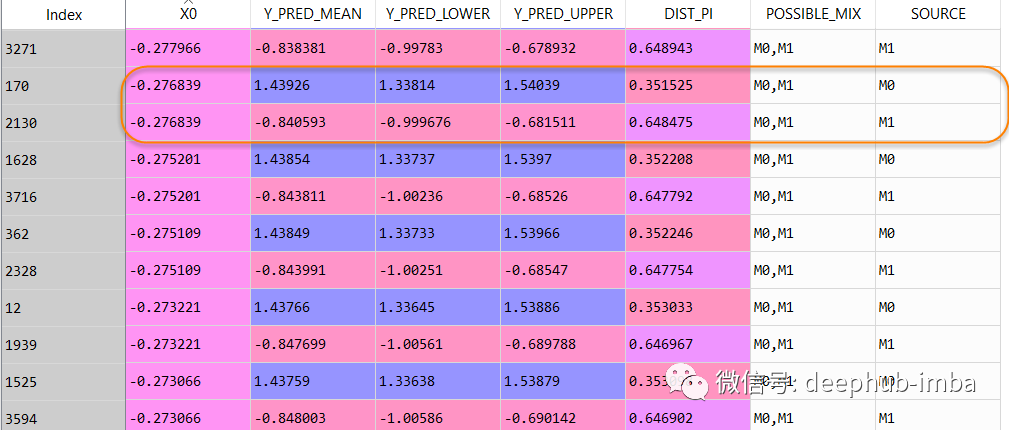
在这个数据表中,当 X = -0.276839 时,Y 可以是 1.43926(混合_0 的概率为 0.351525),但也可以是 -0.840593(混合_1 的概率为 0.648475)。
具有多个分布的实例还提供了重要信息,即数据中正在发生某些事情,并且可能需要更多分析。可能是一些数据质量问题,或者可能表明数据集中缺少一个重要特征!
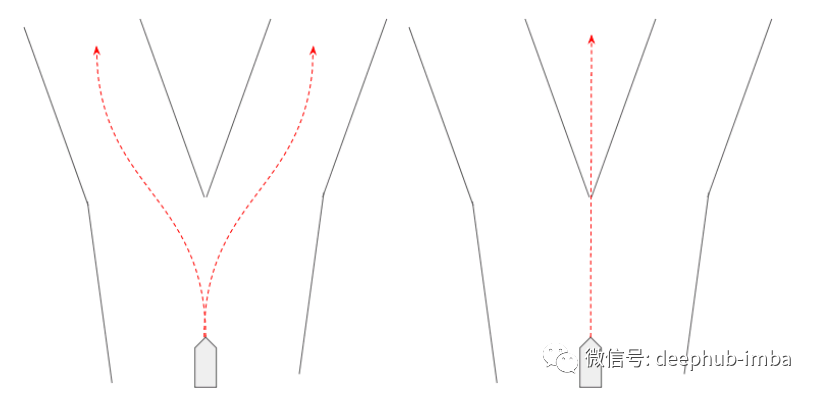
“交通场景预测是可以使用混合密度网络的一个很好的例子。在交通场景预测中,我们需要一个可以表现出的行为分布——例如,一个代理可以左转、右转或直行。因此,混合密度网络可用于表示它学习的每个混合中的“行为”,其中行为由概率和轨迹组成((x,y)坐标在未来某个时间范围内)。
[√] 示例2:具有MDN 的多变量回归
最后MDN 在多元回归问题上表现良好吗?
我们将使用以下的数据集:
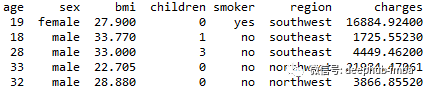
- 年龄:主要受益人的年龄
- 性别:保险承包商性别,女,男
- bmi:体重指数,提供对身体的了解,相对于身高相对较高或较低的体重,使用身高与体重之比的体重客观指数(kg / m ^ 2),理想情况下为18.5到24.9
- 子女:健康保险覆盖的子女人数/受抚养人人数
- 吸烟者:吸烟
- 地区:受益人在美国、东北、东南、西南、西北的居住区。
- 费用:由健康保险计费的个人医疗费用。这是我们要预测的目标
问题陈述是:能否准确预测保险费用(收费)?
现在,让我们导入数据集:
1 | |
数据准备完整可以开始训练了
1 | |
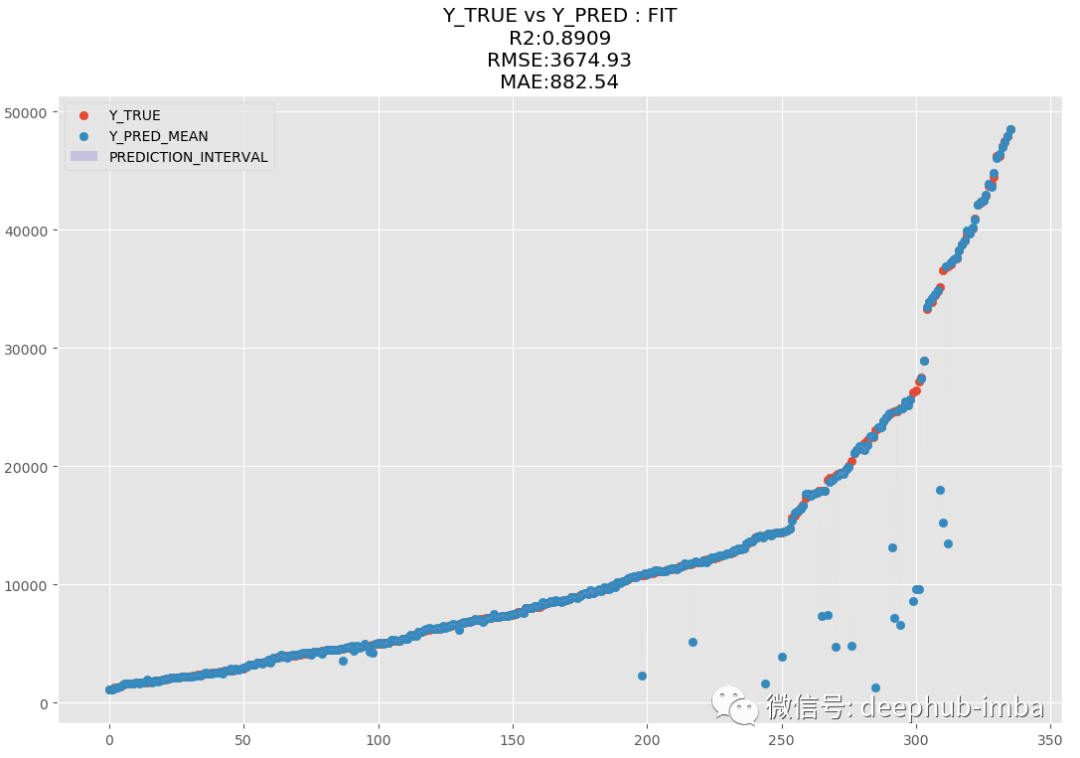
训练完成后使用“最佳混合概率(Pi 参数)策略”预测测试数据集并绘制结果(y_pred vs y_test):
1 | |
1 | |
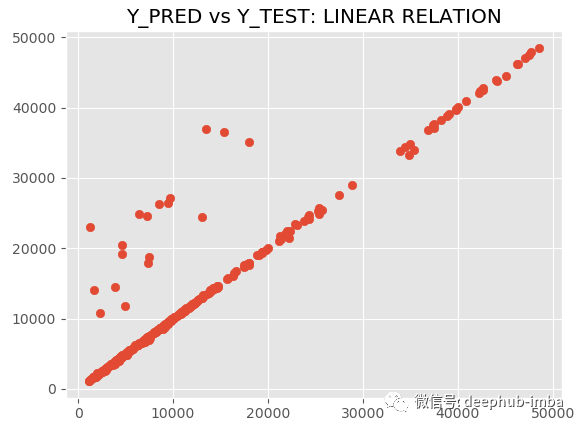
R2 为 89.09,MAE 为 882.54,MDN太棒了,让我们绘制拟合分布与真实分布的图来进行对比:
1 | |
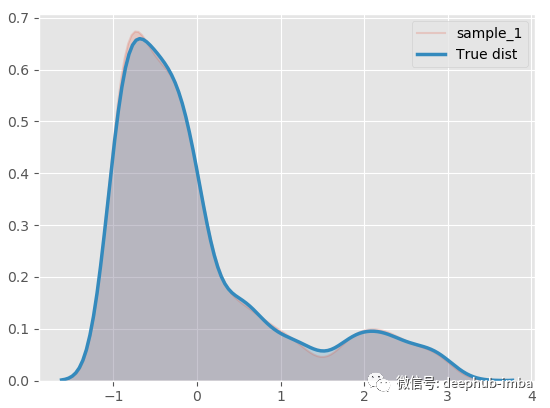
几乎一模一样!分解混合模型,看看什么情况: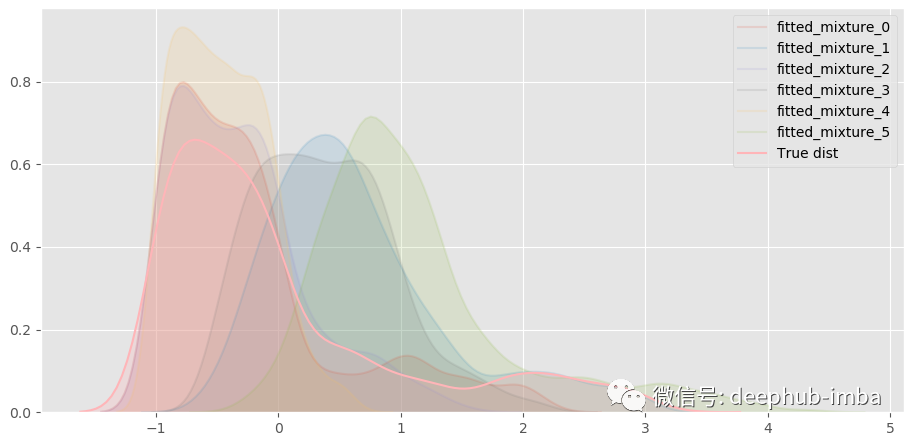
一共混合了六种不同的分布。
从拟合的混合模型生成多变量样本(应用 PCA 以在 2D 中可视化结果):
1 | |
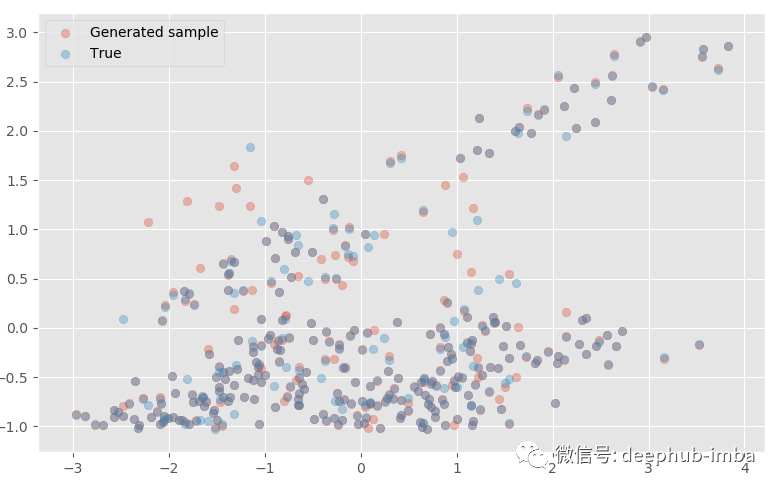
生成的样本与真实样本非常接近!如果我们愿意,还可以从每个分布中进行预测:
1 | |
[√] 总结
- 与线性或非线性经典 ML 模型相比,MDN 在单变量回归数据集中表现出色,其中两个簇相互重叠,并且 X 可能有多个 Y 输出。
- MDN 在多元回归问题上也做得很好,可以与 XGBoost 等流行模型竞争
- MDN 是 ML 中的一款出色且独特的工具,可以解决其他模型无法解决的特定问题(能够从混合分布中获得的数据中学习)
- 随着 MDN 学习分布,还可以通过预测计算不确定性或从学习的分布中生成新样本
本文的代码非常的多,这里是完整的notebook,可以直接下载运行: