第4章 - 前馈神经网络 - 书籍

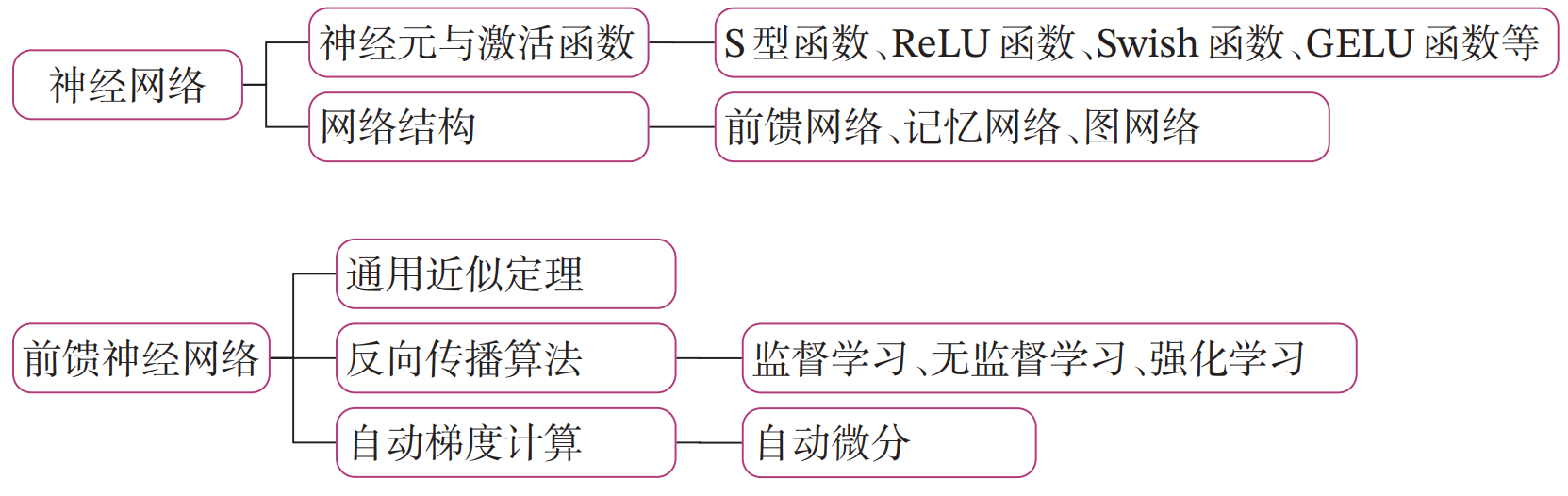
[√] 第4章 - 前馈神经网络

神经网络是由神经元按照一定的连接结构组合而成的网络。神经网络可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射 。
前馈神经网络是最早发明的简单人工神经网络。整个网络中的信息单向传播，可以用一个有向无环路图表示，这种网络结构简单，易于实现。

在学习本章内容前，建议先阅读《神经网络与深度学习》第2章：机器学习概述的相关内容，关键知识点如 图4.1 所示，以便更好的理解和掌握相应的理论知识，及其在实践中的应用方法。

图4.1 《神经网络与深度学习》关键知识点回顾

本实践基于 《神经网络与深度学习》第4章：前馈神经网络 相关内容进行设计，主要包含两部分：

• 模型解读：介绍前馈神经网络的基本概念、网络结构及代码实现，利用前馈神经网络完成一个分类任务，并通过两个简单的实验，观察前馈神经网络的梯度消失问题和死亡ReLU问题，以及对应的优化策略；
• 案例与实践：基于前馈神经网络完成鸢尾花分类任务。

---

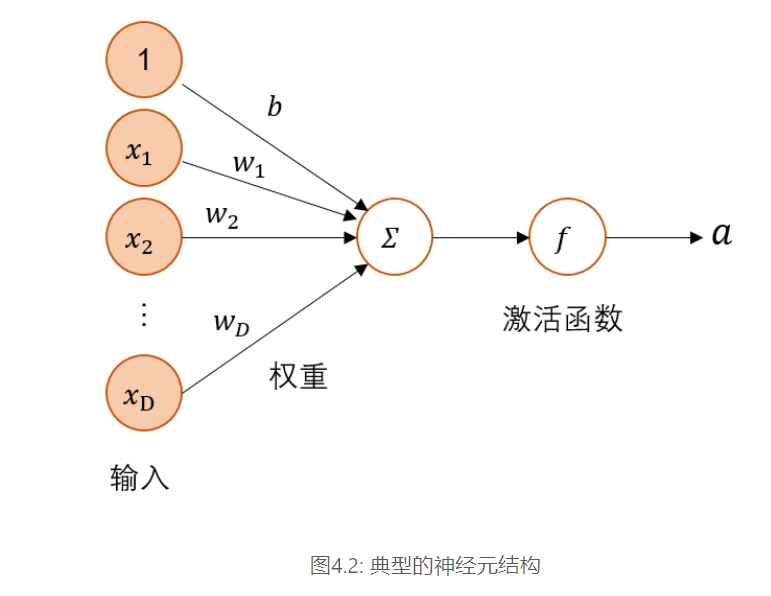
[√] 4.1 - 神经元

神经网络的基本组成单元为带有非线性激活函数的神经元，其结构如如图4.2所示。神经元是对生物神经元的结构和特性的一种简化建模，接收一组输入信号并产生输出。

==带有非线性激活函数==

==接收一组信号并产生输出==

---

[√] 4.1.1 - 净活性值

==z=wx+b 这个公司计算的是净活性值==

假设一个神经元接收的输入为$\mathbf{x}\in \mathbb{R}^D$，其权重向量为$\mathbf{w}\in \mathbb{R}^D$，神经元所获得的输入信号，即净活性值$z$的计算方法为

$$
z =\mathbf{w}^T\mathbf{x}+b，（4.1）
$$

其中$b$为偏置。

为了提高预测样本的效率，我们通常会将$N$个样本归为一组进行成批地预测。

$$
\boldsymbol{z} =\boldsymbol{X} \boldsymbol{w} + b, (4.2)
$$

其中$\boldsymbol{X}\in \mathbb{R}^{N\times D}$为$N$个样本的特征矩阵，$\boldsymbol{z}\in \mathbb{R}^N$为$N$个预测值组成的列向量。

使用Paddle计算一组输入的净活性值。代码实现如下：

import paddle

# 2个特征数为5的样本
X = paddle.rand(shape=[2, 5])

# 含有5个参数的权重向量
w = paddle.rand(shape=[5, 1])
# 偏置项
b = paddle.rand(shape=[1, 1])

# 使用'paddle.matmul'实现矩阵相乘
z = paddle.matmul(X, w) + b
print("input X:", X)
print("weight w:", w, "\nbias b:", b)
print("output z:", z)

input X: Tensor(shape=[2, 5], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0.79964578, 0.80879998, 0.94919258, 0.90140802, 0.99157101],
        [0.68319607, 0.18029618, 0.31775340, 0.69175428, 0.23035321]])
weight w: Tensor(shape=[5, 1], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0.40206695],
        [0.33055961],
        [0.66693956],
        [0.91678756],
        [0.37521145]]) 
bias b: Tensor(shape=[1, 1], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0.04227288]])
output z: Tensor(shape=[2, 1], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[2.46264338],
        [1.30910742]])

说明

在飞桨中，可以使用nn.Linear完成输入张量的上述变换。

---

[√] 4.1.2 - 激活函数

==激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。常用的激活函数有S型函数和ReLU函数。==

净活性值$z$再经过一个非线性函数$f(·)$后，得到神经元的活性值$a$。

$$
a = f(z)，（4.3）
$$

激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。常用的激活函数有S型函数和ReLU函数。

---

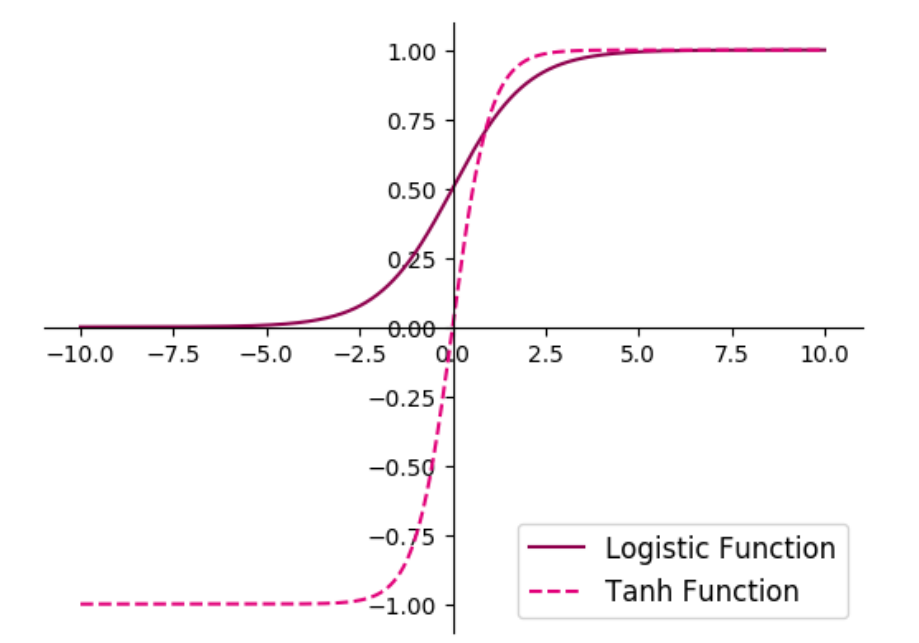
[√] 4.1.2.1 - Sigmoid 型函数

==Sigmoid 型函数是指一类S型曲线函数，为两端饱和函数。==

==常用的 Sigmoid 型函数有 Logistic 函数和 Tanh 函数==

其数学表达式为：

Logistic 函数：

$$
\sigma(z) = \frac{1}{1+\exp(-z)}。（4.4）
$$

Tanh 函数：

$$
\mathrm{tanh}(z) = \frac{\exp(z)-\exp(-z)}{\exp(z)+\exp(-z)}。（4.5）
$$

Logistic函数和Tanh函数的代码实现和可视化如下：

%matplotlib inline
import matplotlib.pyplot as plt

# Logistic函数
def logistic(z):
    return 1.0 / (1.0 + paddle.exp(-z))

# Tanh函数
def tanh(z):
    return (paddle.exp(z) - paddle.exp(-z)) / (paddle.exp(z) + paddle.exp(-z))

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = paddle.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), logistic(z).tolist(), color='#8E004D', label="Logistic Function")
plt.plot(z.tolist(), tanh(z).tolist(), color='#E20079', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

说明

在飞桨中，可以通过调用paddle.nn.functional.sigmoid和paddle.nn.functional.tanh实现对张量的Logistic和Tanh计算。

---

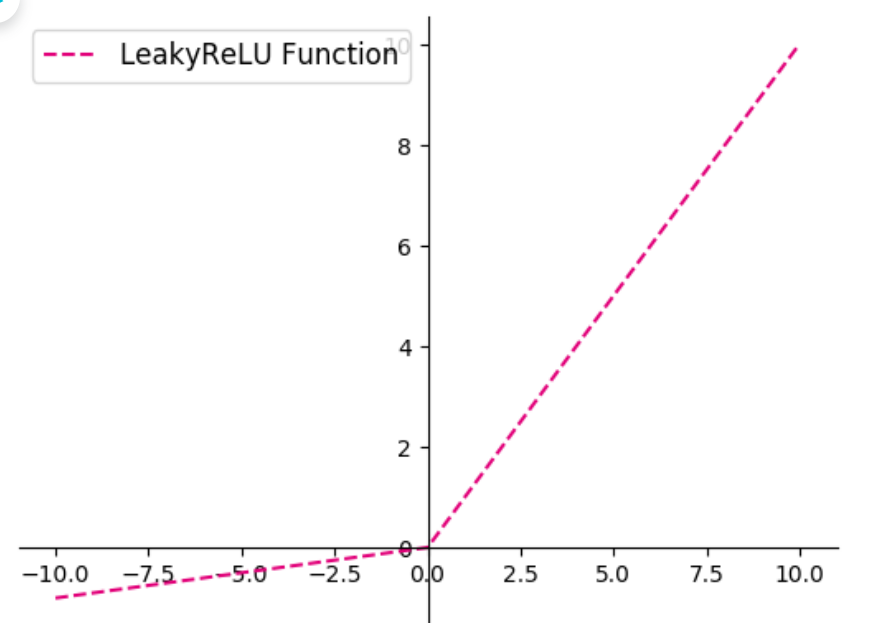
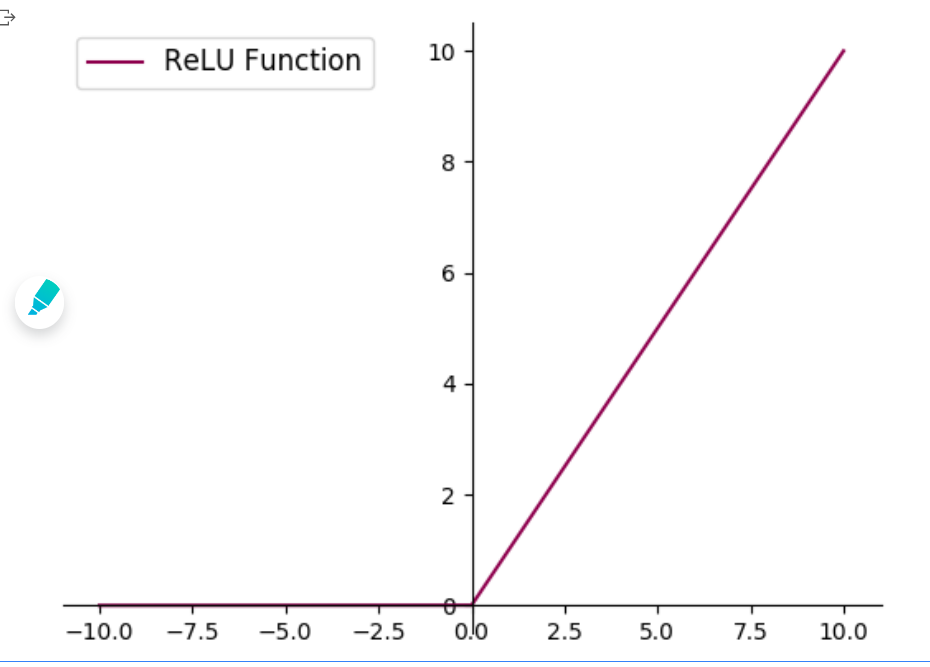
[√] 4.1.2.2 - ReLU 型函数

常见的ReLU函数有ReLU和带泄露的ReLU（Leaky ReLU），数学表达式分别为：

$$
\mathrm{ReLU}(z) = \max(0,z),（4.6）
$$

$$
\mathrm{LeakyReLU}(z) = \max(0,z)+\lambda \min(0,z),（4.7）
$$

其中$\lambda$为超参数。

可视化ReLU和带泄露的ReLU的函数的代码实现和可视化如下：

# ReLU
def relu(z):
    return paddle.maximum(z, paddle.to_tensor(0.))

# 带泄露的ReLU
def leaky_relu(z, negative_slope=0.1):
    # 当前版本paddle暂不支持直接将bool类型转成int类型，因此调用了paddle的cast函数来进行显式转换
    a1 = (paddle.cast((z > 0), dtype='float32') * z) 
    a2 = (paddle.cast((z <= 0), dtype='float32') * (negative_slope * z))
    return a1 + a2

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = paddle.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z.tolist(), relu(z).tolist(), color="#8E004D", label="ReLU Function")
plt.plot(z.tolist(), leaky_relu(z).tolist(), color="#E20079", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

说明

在飞桨中，可以通过调用paddle.nn.functional.relu和paddle.nn.functional.leaky_relu完成ReLU与带泄露的ReLU的计算。

---

动手练习
本节重点介绍和实现了几个经典的Sigmoid函数和ReLU函数。
请动手实现《神经网络与深度学习》4.1节中提到的其他激活函数，如：Hard-Logistic、Hard-Tanh、ELU、Softplus、Swish等。

---

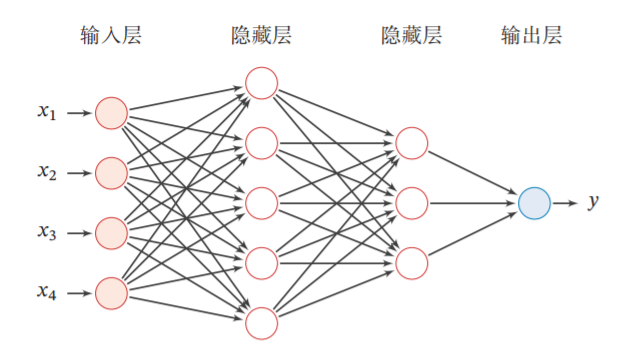
[√] 4.2 - 基于前馈神经网络的二分类任务

前馈神经网络的网络结构如图4.3所示。每一层获取前一层神经元的活性值，并重复上述计算得到该层的活性值，传入到下一层。整个网络中无反馈，信号从输入层向输出层逐层的单向传播，得到网络最后的输出 $\boldsymbol{a}^{(L)}$。

图4.3: 前馈神经网络结构

---

[√] 4.2.1 - 数据集构建

这里，我们使用第3.1.1节中构建的二分类数据集：Moon1000数据集，其中训练集640条、验证集160条、测试集200条。 该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征。

from nndl.dataset import make_moons

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)

num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

outer_circ_x.shape: [500] outer_circ_y.shape: [500]
inner_circ_x.shape: [500] inner_circ_y.shape: [500]
after concat shape: [1000]
X shape: [1000, 2]
y shape: [1000]

---

[√] 4.2.2 - 模型构建

==经过仿射变换，得到该层神经元的净活性值z==

==再输入到激活函数得到该层神经元的活性值a==

==在实践中，为了提高模型的处理效率，通常将N个样本归为一组进行成批地计算。==

为了更高效的构建前馈神经网络，我们先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。

假设网络的第$l$层的输入为第$l-1$层的神经元活性值$\boldsymbol{a}^{(l-1)}$，经过一个仿射变换，得到该层神经元的净活性值$\boldsymbol{z}$，再输入到激活函数得到该层神经元的活性值$\boldsymbol{a}$。

在实践中，为了提高模型的处理效率，通常将$N$个样本归为一组进行成批地计算。假设网络第$l$层的输入为$\boldsymbol{A}^{(l-1)}\in \mathbb{R}^{N\times M_{l-1}}$，其中每一行为一个样本，则前馈网络中第$l$层的计算公式为

$$
\mathbf Z^{(l)}=\mathbf A^{(l-1)} \mathbf W^{(l)} +\mathbf b^{(l)} \in \mathbb{R}^{N\times M_{l}}, (4.8)
$$
$$
\mathbf A^{(l)}=f_l(\mathbf Z^{(l)}) \in \mathbb{R}^{N\times M_{l}}, (4.9)
$$
其中$\mathbf Z^{(l)}$为$N$个样本第$l$层神经元的净活性值，$\mathbf A^{(l)}$为$N$个样本第$l$层神经元的活性值，$\boldsymbol{W}^{(l)}\in \mathbb{R}^{M_{l-1}\times M_{l}}$为第$l$层的权重矩阵，$\boldsymbol{b}^{(l)}\in \mathbb{R}^{1\times M_{l}}$为第$l$层的偏置。

---

为了和代码的实现保存一致性，这里使用形状为$(样本数量\times 特征维度)$的张量来表示一组样本。样本的矩阵$\boldsymbol{X}$是由$N$个$\boldsymbol{x}$的行向量组成。而《神经网络与深度学习》中$\boldsymbol{x}$为列向量，因此这里的权重矩阵$\boldsymbol{W}$和偏置$\boldsymbol{b}$和《神经网络与深度学习》中的表示刚好为转置关系。

---

为了使后续的模型搭建更加便捷，我们将神经层的计算，即公式(4.8)和(4.9)，都封装成算子，这些算子都继承Op基类。

---

[√] 4.2.2.1 - 线性层算子

公式（4.8）对应一个线性层算子，权重参数采用默认的随机初始化，偏置采用默认的零初始化。代码实现如下：

from nndl.op import Op

# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=paddle.standard_normal, bias_init=paddle.zeros):
        """
        输入：
            - input_size：输入数据维度
            - output_size：输出数据维度
            - name：算子名称
            - weight_init：权重初始化方式，默认使用'paddle.standard_normal'进行标准正态分布初始化
            - bias_init：偏置初始化方式，默认使用全0初始化
        """
        
        self.params = {}
        # 初始化权重
        self.params['W'] = weight_init(shape=[input_size,output_size])
        # 初始化偏置
        self.params['b'] = bias_init(shape=[1,output_size])
        self.inputs = None

        self.name = name

    def forward(self, inputs):
        """
        输入：
            - inputs：shape=[N,input_size], N是样本数量
        输出：
            - outputs：预测值，shape=[N,output_size]
        """
        self.inputs = inputs

        outputs = paddle.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

---

[√] 4.2.2.2 - Logistic算子

本节我们采用Logistic函数来作为公式(4.9)中的激活函数。这里也将Logistic函数实现一个算子，代码实现如下：

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D]
        输出：
            - outputs：shape=[N,D]
        """
        outputs = 1.0 / (1.0 + paddle.exp(-inputs))
        self.outputs = outputs
        return outputs

---

[√] 4.2.2.3 - 层的串行组合

==在定义了神经层的线性层算子和激活函数算子之后，我们可以不断交叉重复使用它们来构建一个多层的神经网络。==

==使用激活函数的作用是为了激活特征，让特征更有活力。将特征归一化，这样可以防止过拟合，通过这种正则化方式抑制模型的能力。通过归一化特征值，可以防止特征值量纲的不同导致的差异。==

下面我们实现一个两层的用于二分类任务的前馈神经网络，选用Logistic作为激活函数，可以利用上面实现的线性层和激活函数算子来组装。代码实现如下：

# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        """
        输入：
            - input_size：输入维度
            - hidden_size：隐藏层神经元数量
            - output_size：输出维度
        """
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        输入：
            - X：shape=[N,input_size], N是样本数量
        输出：
            - a2：预测值，shape=[N,output_size]
        """
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

测试一下

现在，我们实例化一个两层的前馈网络，令其输入层维度为5，隐藏层维度为10，输出层维度为1。 并随机生成一条长度为5的数据输入两层神经网络，观察输出结果。

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)
# 随机生成1条长度为5的数据
X = paddle.rand(shape=[1, 5])
result = model(X)
print ("result: ", result)

result:  Tensor(shape=[1, 1], dtype=float32, place=CPUPlace, stop_gradient=True,
       [[0.65805507]])

---

[√] 4.2.3 - 损失函数

二分类交叉熵损失函数见第三章，这里不再赘述。

---

[√] 4.2.4 - 模型优化

==神经网络的参数主要是通过梯度下降法进行优化的，因此需要计算最终损失对每个参数的梯度。==

==由于神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。==

---

[√] 4.2.4.1 - 反向传播算法

前馈神经网络的参数梯度通常使用误差反向传播算法来计算。使用误差反向传播算法的前馈神经网络训练过程可以分为以下三步：

1. 前馈计算每一层的净活性值$\boldsymbol{Z}^{(l)}$和激活值$\boldsymbol{A}^ {(l)}$，直到最后一层；
2. 反向传播计算每一层的误差项$\delta^{(l)}=\frac{\partial R}{\partial \boldsymbol{Z}^{(l)}}$；
3. 计算每一层参数的梯度，并更新参数。

在上面实现算子的基础上，来实现误差反向传播算法。在上面的三个步骤中，

1. 第1步是前向计算，可以利用算子的forward()方法来实现；
2. 第2步是反向计算梯度，可以利用算子的backward()方法来实现；
3. 第3步中的计算参数梯度也放到backward()中实现，更新参数放到另外的优化器中专门进行。

这样，在模型训练过程中，我们首先执行模型的forward()，再执行模型的backward()，就得到了所有参数的梯度，之后再利用优化器迭代更新参数。

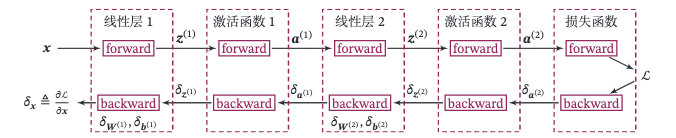
以这我们这节中构建的两层全连接前馈神经网络Model_MLP_L2为例，下图给出了其前向和反向计算过程：

下面我们按照反向的梯度传播顺序，为每个算子添加backward()方法，并在其中实现每一层参数的梯度的计算。

---

[√] 4.2.4.2 - 损失函数

二分类交叉熵损失函数对神经网络的输出$\hat{\boldsymbol{y}}$的偏导数为:
$$
\frac{\partial R}{\partial \hat{\boldsymbol{y}}} = -\frac{1}{N}(\mathrm{dialog}(\frac{1}{\hat{\boldsymbol{y}}})\boldsymbol{y}-\mathrm{dialog}(\frac{1}{1-\hat{\boldsymbol{y}}})(1-\boldsymbol{y})) (4.10) \
= -\frac{1}{N}(\frac{1}{\hat{\boldsymbol{y}}}\odot\boldsymbol{y}-\frac{1}{1-\hat{\boldsymbol{y}}}\odot(1-\boldsymbol{y})), (4.11)
$$
其中$dialog(\boldsymbol{x})$表示以向量$\boldsymbol{x}$为对角元素的对角阵，$\frac{1}{\boldsymbol{x}}=\frac{1}{x_1},…,\frac{1}{x_N}$表示逐元素除，$\odot$表示逐元素积。

• 实现损失函数的backward()，代码实现如下：

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (paddle.matmul(self.labels.t(), paddle.log(self.predicts)) 
                + paddle.matmul((1-self.labels.t()), paddle.log(1-self.predicts)))

        loss = paddle.squeeze(loss, axis=1)
        return loss

    def backward(self):
        # 计算损失函数对模型预测的导数
        loss_grad_predicts = -1.0 * (self.labels / self.predicts - 
                       (1 - self.labels) / (1 - self.predicts)) / self.num
        
        # 梯度反向传播
        self.model.backward(loss_grad_predicts)

---

[√] 4.2.4.3 - Logistic算子

在本节中，我们使用Logistic激活函数，所以这里为Logistic算子增加的反向函数。

Logistic算子的前向过程表示为$\boldsymbol{A}=\sigma(\boldsymbol{Z})$，其中$\sigma$为Logistic函数，$\boldsymbol{Z} \in R^{N \times D}$和$\boldsymbol{A} \in R^{N \times D}$的每一行表示一个样本。

为了简便起见，我们分别用向量$\boldsymbol{a} \in R^D$ 和 $\boldsymbol{z} \in R^D$表示同一个样本在激活函数前后的表示，则$\boldsymbol{a}$对$\boldsymbol{z}$的偏导数为：
$$
\frac{\partial \boldsymbol{a}}{\partial \boldsymbol{z}}=diag(\boldsymbol{a}\odot(1-\boldsymbol{a}))\in R^{D \times D}, (4.12)
$$
按照反向传播算法，令$\delta_{\boldsymbol{a}}=\frac{\partial R}{\partial \boldsymbol{a}} \in R^D$表示最终损失$R$对Logistic算子的单个输出$\boldsymbol{a}$的梯度，则
$$
\delta_{\boldsymbol{z}} \triangleq \frac{\partial R}{\partial \boldsymbol{z}} = \frac{\partial \boldsymbol{a}}{\partial \boldsymbol{z}}\delta_{\boldsymbol{a}} (4.13) \
= diag(\boldsymbol{a}\odot(1-\boldsymbol{a}))\delta_{\boldsymbol(a)}, (4.14) \
= \boldsymbol{a}\odot(1-\boldsymbol{a})\odot\delta_{\boldsymbol(a)}。 (4.15)
$$

将上面公式利用批量数据表示的方式重写，令$\delta_{\boldsymbol{A}} =\frac{\partial R}{\partial \boldsymbol{A}} \in R^{N \times D}$表示最终损失$R$对Logistic算子输出$A$的梯度，损失函数对Logistic函数输入$\boldsymbol{Z}$的导数为
$$
\delta_{\boldsymbol{Z}}=\boldsymbol{A} \odot (1-\boldsymbol{A})\odot \delta_{\boldsymbol{A}} \in R^{N \times D},(4.16)
$$
$\delta_{\boldsymbol{Z}}$为Logistic算子反向传播的输出。

由于Logistic函数中没有参数，这里不需要在backward()方法中计算该算子参数的梯度。

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + paddle.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = paddle.multiply(self.outputs, (1.0 - self.outputs))
        return paddle.multiply(grads,outputs_grad_inputs)

---

[√] 4.2.4.4 - 线性层

线性层算子Linear的前向过程表示为$\boldsymbol{Y}=\boldsymbol{X}\boldsymbol{W}+\boldsymbol{b}$，其中输入为$\boldsymbol{X} \in R^{N \times M}$，输出为$\boldsymbol{Y} \in R^{N \times D}$，参数为权重矩阵$\boldsymbol{W} \in R^{M \times D}$和偏置$\boldsymbol{b} \in R^{1 \times D}$。$\boldsymbol{X}$和$\boldsymbol{Y}$中的每一行表示一个样本。

为了简便起见，我们用向量$\boldsymbol{x}\in R^M$和$\boldsymbol{y}\in R^D$表示同一个样本在线性层算子中的输入和输出，则有$\boldsymbol{y}=\boldsymbol{W}^T\boldsymbol{x}+\boldsymbol{b}^T$。$\boldsymbol{y}$对输入$\boldsymbol{x}$的偏导数为
$$
\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = \boldsymbol{W}\in R^{D \times M}。(4.17)
$$

==线性层输入的梯度==

按照反向传播算法，令$\delta_{\boldsymbol{y}}=\frac{\partial R}{\partial \boldsymbol{y}}\in R^D$表示最终损失$R$对线性层算子的单个输出$\boldsymbol{y}$的梯度，则
$$
\delta_{\boldsymbol{x}} \triangleq \frac{\partial R}{\partial \boldsymbol{x}}= \boldsymbol{W} \delta_{\boldsymbol{y}}。(4.18)
$$

将上面公式利用批量数据表示的方式重写，令$\delta_{\boldsymbol{Y}}=\frac{\partial R}{\partial \boldsymbol{Y}}\in \mathbb{R}^{N\times D}$表示最终损失$R$对线性层算子输出$\boldsymbol{Y}$的梯度，公式可以重写为
$$
\delta_{\boldsymbol{X}} =\delta_{\boldsymbol{Y}} \boldsymbol{W}^T,(4.19)
$$
其中$\delta_{\boldsymbol{X}}$为线性层算子反向函数的输出。

==线性层参数的梯度==

计算线性层参数的梯度 由于线性层算子中包含有可学习的参数$\boldsymbol{W}$和$\boldsymbol{b}$，因此backward()除了实现梯度反传外，还需要计算算子内部的参数的梯度。

令$\delta_{\boldsymbol{y}}=\frac{\partial R}{\partial \boldsymbol{y}}\in \mathbb{R}^D$表示最终损失$R$对线性层算子的单个输出$\boldsymbol{y}$的梯度，则
$$
\delta_{\boldsymbol{W}} \triangleq \frac{\partial R}{\partial \boldsymbol{W}} = \boldsymbol{x}\delta_{\boldsymbol{y}}^T,(4.20) \
\delta_{\boldsymbol{b}} \triangleq \frac{\partial R}{\partial \boldsymbol{b}} = \delta_{\boldsymbol{y}}^T。(4.21)
$$

将上面公式利用批量数据表示的方式重写，令$\delta_{\boldsymbol{Y}}=\frac{\partial R}{\partial \boldsymbol{Y}}\in \mathbb{R}^{N\times D}$表示最终损失$R$对线性层算子输出$\boldsymbol{Y}$的梯度，则公式可以重写为
$$
\delta_{\boldsymbol{W}} = \boldsymbol{X}^T \delta_{\boldsymbol{Y}},(4.22) \
\delta_{\boldsymbol{b}} = \mathbf{1}^T \delta_{\boldsymbol{Y}}。(4.23)
$$

具体实现代码如下：

class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=paddle.standard_normal, bias_init=paddle.zeros):
        self.params = {}
        self.params['W'] = weight_init(shape=[input_size, output_size])
        self.params['b'] = bias_init(shape=[1, output_size])

        self.inputs = None
        self.grads = {}

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs
        outputs = paddle.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        """
        输入：
            - grads：损失函数对当前层输出的导数
        输出：
            - 损失函数对当前层输入的导数
        """
        self.grads['W'] = paddle.matmul(self.inputs.T, grads)
        self.grads['b'] = paddle.sum(grads, axis=0)

        # 线性层输入的梯度
        return paddle.matmul(grads, self.params['W'].T)

---

[√] 4.2.4.5 - 整个网络

实现完整的两层神经网络的前向和反向计算。代码实现如下：

class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        # 线性层
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        # Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]

    def __call__(self, X):
        return self.forward(X)

    # 前向计算
    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2
        
    # 反向计算，因为是反向传播，因此对输入的倒数，通过对输出的倒数推得，←
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

---

[√] 4.2.4.6 - 优化器

在计算好神经网络参数的梯度之后，我们将梯度下降法中参数的更新过程实现在优化器中。

与第3章中实现的梯度下降优化器SimpleBatchGD不同的是，此处的优化器需要遍历每层，对每层的参数分别做更新。

from nndl.opitimizer import Optimizer

class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

---

[√] 4.2.5 - 完善Runner类：RunnerV2_1

基于3.1.6实现的 RunnerV2 类主要针对比较简单的模型。而在本章中，模型由多个算子组合而成，通常比较复杂，因此本节继续完善并实现一个改进版： RunnerV2_1类，其主要加入的功能有：

1. 支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；
2. 每层的模型保存和加载，将每一层的参数分别进行保存和加载。

import os

class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)

        # 传入模型保存路径
        save_dir = kwargs.get("save_dir", None)
        
        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y) # return a tensor
            
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            # alec：此处是主动计算梯度
            self.loss_fn.backward() # 反向传播计算梯度

            # 参数更新
            self.optimizer.step() # 梯度下降方法更新梯度
           
            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
    
    # 验证不需要计算梯度和更新参数
    def evaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss
    
    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        # 对模型每层参数分别进行保存，保存文件名称与该层名称相同
        # 按层保存模型
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                paddle.save(layer.params, os.path.join(save_dir, layer.name+".pdparams"))

    def load_model(self, model_dir):
        # 获取所有层参数名称和保存路径之间的对应关系
        model_file_names = os.listdir(model_dir)
        name_file_dict = {}
        for file_name in model_file_names:
            name = file_name.replace(".pdparams","")
            name_file_dict[name] = os.path.join(model_dir, file_name)

        # 加载每层参数
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                name = layer.name
                file_path = name_file_dict[name]
                layer.params = paddle.load(file_path)

---

[√] 4.2.6 - 模型训练

基于RunnerV2_1，使用训练集和验证集进行模型训练，共训练2000个epoch。评价指标为第章介绍的accuracy。代码实现如下：

from nndl.metric import accuracy
paddle.seed(123)
epoch_num = 1000

model_saved_dir = "model"

# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 5
# 输出层维度为1
output_size = 1

# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)

# 优化器
learning_rate = 0.2
optimizer = BatchGD(learning_rate, model)

# 评价方法
metric = accuracy

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

运行耗时: 2秒843毫秒
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.20000
[Train] epoch: 0/1000, loss: 0.7360124588012695
[Evaluate] best accuracy performence has been updated: 0.20000 --> 0.21875
[Evaluate] best accuracy performence has been updated: 0.21875 --> 0.29375
[Evaluate] best accuracy performence has been updated: 0.29375 --> 0.32500
[Evaluate] best accuracy performence has been updated: 0.32500 --> 0.39375
[Evaluate] best accuracy performence has been updated: 0.39375 --> 0.44375
[Evaluate] best accuracy performence has been updated: 0.44375 --> 0.67500
[Evaluate] best accuracy performence has been updated: 0.67500 --> 0.70000
[Evaluate] best accuracy performence has been updated: 0.70000 --> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 --> 0.72500
[Evaluate] best accuracy performence has been updated: 0.72500 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.75625
[Evaluate] best accuracy performence has been updated: 0.75625 --> 0.76250
[Evaluate] best accuracy performence has been updated: 0.76250 --> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.77500
[Evaluate] best accuracy performence has been updated: 0.77500 --> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.78750
[Train] epoch: 50/1000, loss: 0.6630627512931824
[Evaluate] best accuracy performence has been updated: 0.78750 --> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 --> 0.80000
[Train] epoch: 100/1000, loss: 0.5919685959815979
[Train] epoch: 150/1000, loss: 0.5248624086380005
[Evaluate] best accuracy performence has been updated: 0.80000 --> 0.80625
[Evaluate] best accuracy performence has been updated: 0.80625 --> 0.81250
[Evaluate] best accuracy performence has been updated: 0.81250 --> 0.81875
[Train] epoch: 200/1000, loss: 0.48363637924194336
[Evaluate] best accuracy performence has been updated: 0.81875 --> 0.82500
[Evaluate] best accuracy performence has been updated: 0.82500 --> 0.83125
[Train] epoch: 250/1000, loss: 0.46238335967063904
[Train] epoch: 300/1000, loss: 0.4515562951564789
[Evaluate] best accuracy performence has been updated: 0.83125 --> 0.83750
[Train] epoch: 350/1000, loss: 0.44589540362358093
[Train] epoch: 400/1000, loss: 0.44286662340164185
[Evaluate] best accuracy performence has been updated: 0.83750 --> 0.84375
[Train] epoch: 450/1000, loss: 0.44121456146240234
[Evaluate] best accuracy performence has been updated: 0.84375 --> 0.85000
[Train] epoch: 500/1000, loss: 0.44029098749160767
[Train] epoch: 550/1000, loss: 0.43975430727005005
[Train] epoch: 600/1000, loss: 0.4394233822822571
[Train] epoch: 650/1000, loss: 0.43920236825942993
[Train] epoch: 700/1000, loss: 0.4390408992767334
[Train] epoch: 750/1000, loss: 0.4389124810695648
[Train] epoch: 800/1000, loss: 0.43880319595336914
[Train] epoch: 850/1000, loss: 0.4387057423591614
[Train] epoch: 900/1000, loss: 0.43861618638038635
[Train] epoch: 950/1000, loss: 0.43853235244750977

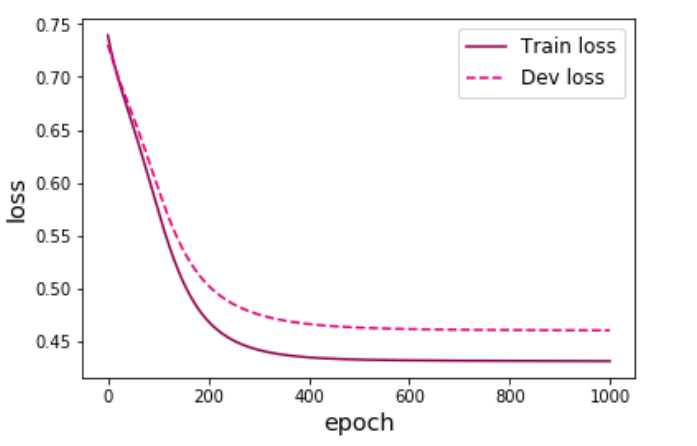
可视化观察训练集与验证集的损失函数变化情况。

# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#8E004D", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#E20079", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='x-large')
plt.ylabel("loss", fontsize='x-large')
plt.legend(fontsize='large')
plt.savefig('fw-loss2.pdf')
plt.show()

---

[√] 4.2.7 - 性能评价

使用测试集对训练中的最优模型进行评价，观察模型的评价指标。代码实现如下：

# 加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

[Test] score/loss: 0.8350/0.4016

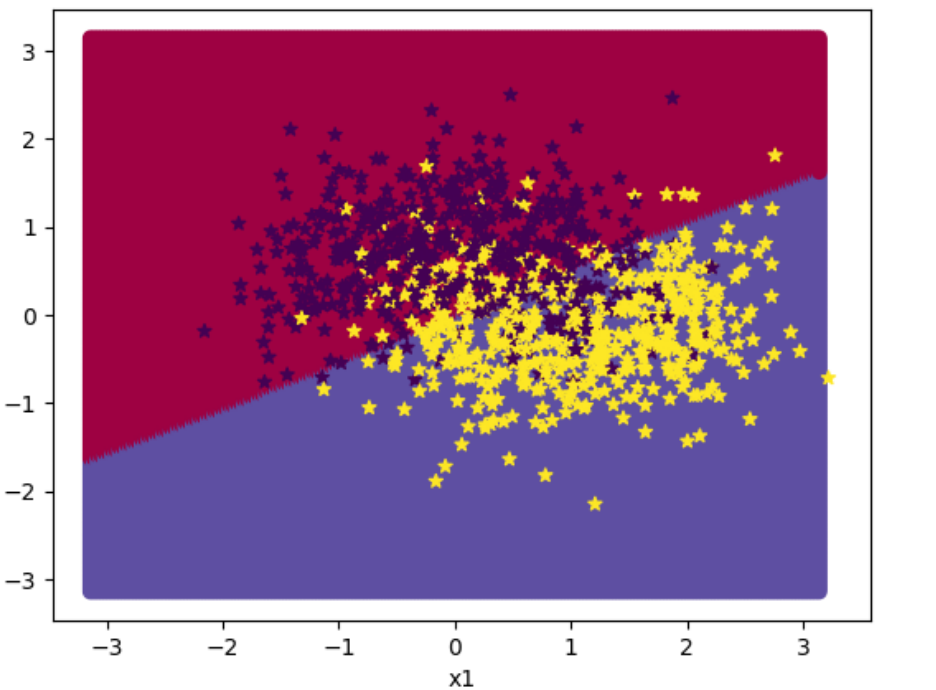
从结果来看，模型在测试集上取得了较高的准确率。

下面对结果进行可视化：

import math

# 均匀生成40000个数据点
x1, x2 = paddle.meshgrid(paddle.linspace(-math.pi, math.pi, 200), paddle.linspace(-math.pi, math.pi, 200))
x = paddle.stack([paddle.flatten(x1), paddle.flatten(x2)], axis=1)

# 预测对应类别
y = runner.predict(x)
y = paddle.squeeze(paddle.cast((y>=0.5),dtype='float32'),axis=-1)

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=paddle.squeeze(y_train,axis=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=paddle.squeeze(y_dev,axis=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=paddle.squeeze(y_test,axis=-1).tolist())

---

[√] 4.3 - 自动梯度计算和预定义算子

虽然我们能够通过模块化的方式比较好地对神经网络进行组装，但是每个模块的梯度计算过程仍然十分繁琐且容易出错。在深度学习框架中，已经封装了自动梯度计算的功能，我们只需要聚焦模型架构，不再需要耗费精力进行计算梯度。

飞桨提供了paddle.nn.Layer类，来方便快速的实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。

继承了paddle.nn.Layer类的算子中，可以在内部直接调用其它继承paddle.nn.Layer类的算子，飞桨框架会自动识别算子中内嵌的paddle.nn.Layer类算子，并自动计算它们的梯度，并在优化时更新它们的参数。

---

[√] 4.3.1 - 利用预定义算子重新实现前馈神经网络

下面我们使用Paddle的预定义算子来重新实现二分类任务。 主要使用到的预定义算子为paddle.nn.Linear：

class paddle.nn.Linear(in_features, out_features, weight_attr=None, bias_attr=None, name=None)

paddle.nn.Linear算子可以接受一个形状为[batch_size,∗,in_features]的输入张量，其中”∗”表示张量中可以有任意的其它额外维度，并计算它与形状为[in_features, out_features]的权重矩阵的乘积，然后生成形状为[batch_size,∗,out_features]的输出张量。 paddle.nn.Linear算子默认有偏置参数，可以通过bias_attr=False设置不带偏置。

---

paddle.nn 目录下包含飞桨框架支持的神经网络层和相关函数的相关API。paddle.nn.functional下都是一些函数实现。

---

代码实现如下：

import paddle.nn as nn
import paddle.nn.functional as F
from paddle.nn.initializer import Constant, Normal, Uniform

class Model_MLP_L2_V2(paddle.nn.Layer):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size,
                                weight_attr=paddle.ParamAttr(initializer=Normal(mean=0., std=1.)),
                                bias_attr=paddle.ParamAttr(initializer=Constant(value=0.0)))
        self.fc2 = nn.Linear(hidden_size, output_size,
                                weight_attr=paddle.ParamAttr(initializer=Normal(mean=0., std=1.)),
                                bias_attr=paddle.ParamAttr(initializer=Constant(value=0.0)))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = F.sigmoid
        
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

---

[√] 4.3.2 - 完善Runner类

基于上一节实现的 RunnerV2_1 类，本节的 RunnerV2_2 类在训练过程中使用自动梯度计算；模型保存时，使用state_dict方法获取模型参数；模型加载时，使用set_state_dict方法加载模型参数.

class RunnerV2_2(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        # log打印函数，如果没有传入则默认为"None"
        custom_print_log = kwargs.get("custom_print_log", None) 
        
        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            # 自动计算参数梯度
            # alec：此处通过trn_loss自动计算梯度
            trn_loss.backward()
            if custom_print_log is not None:
                # 打印每一层的梯度
                custom_print_log(self)

            # 参数更新
            self.optimizer.step()
            # 清空梯度
            self.optimizer.clear_grad()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
                
    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @paddle.no_grad()
    def evaluate(self, data_set):
        # 将模型切换为评估模式
        self.model.eval()

        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss
    
    # 模型测试阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @paddle.no_grad()
    def predict(self, X):
        # 将模型切换为评估模式
        self.model.eval()
        return self.model(X)

    # 使用'model.state_dict()'获取模型参数，并进行保存
    def save_model(self, saved_path):
        paddle.save(self.model.state_dict(), saved_path)

    # 使用'model.set_state_dict'加载模型参数
    def load_model(self, model_path):
        state_dict = paddle.load(model_path)
        self.model.set_state_dict(state_dict)

---

[√] 4.3.3 - 模型训练

实例化RunnerV2类，并传入训练配置，代码实现如下：

# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 设置损失函数
loss_fn = F.binary_cross_entropy

# 设置优化器
learning_rate = 0.2
optimizer = paddle.optimizer.SGD(learning_rate=learning_rate, parameters=model.parameters())

# 设置评价指标
metric = accuracy

# 其他参数
epoch_num = 1000
saved_path = 'best_model.pdparams'

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_path="best_model.pdparams")

将训练过程中训练集与验证集的准确率变化情况进行可视化。

# 可视化观察训练集与验证集的指标变化情况
def plot(runner, fig_name):
    plt.figure(figsize=(10,5))
    epochs = [i for i in range(len(runner.train_scores))]

    plt.subplot(1,2,1)
    plt.plot(epochs, runner.train_loss, color='#8E004D', label="Train loss")
    plt.plot(epochs, runner.dev_loss, color='#E20079', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='x-large')
    plt.xlabel("epoch", fontsize='x-large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.subplot(1,2,2)
    plt.plot(epochs, runner.train_scores, color='#8E004D', label="Train accuracy")
    plt.plot(epochs, runner.dev_scores, color='#E20079', linestyle='--', label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='x-large')
    plt.xlabel("epoch", fontsize='x-large')
    plt.legend(loc='lower right', fontsize='x-large')
    
    plt.savefig(fig_name)
    plt.show()

plot(runner, 'fw-acc.pdf')

---

[√] 4.3.4 - 性能评价

使用测试数据对训练完成后的最优模型进行评价，观察模型在测试集上的准确率以及loss情况。代码如下：

# 模型评价
runner.load_model("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行耗时: 7毫秒
[Test] score/loss: 0.8300/0.4035

从结果来看，模型在测试集上取得了较高的准确率。

---

[√] 4.4 - 优化问题

在本节中，我们通过实践来发现神经网络模型的优化问题，并思考如何改进。

---

[√] 4.4.1 - 参数初始化

实现一个神经网络前，需要先初始化模型参数。如果对每一层的权重和偏置都用0初始化，那么通过第一遍前向计算，所有隐藏层神经元的激活值都相同；在反向传播时，所有权重的更新也都相同，这样会导致隐藏层神经元没有差异性，出现对称权重现象。

接下来，将模型参数全都初始化为0，看实验结果。这里重新定义了一个类TwoLayerNet_Zeros，两个线性层的参数全都初始化为0。

import paddle.nn as nn
import paddle.nn.functional as F
from paddle.nn.initializer import Constant, Normal, Uniform

class Model_MLP_L2_V4(paddle.nn.Layer):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中in_features为线性层输入维度；out_features为线性层输出维度
        # weight_attr为权重参数属性
        # bias_attr为偏置参数属性
        self.fc1 = nn.Linear(input_size, hidden_size,
                                weight_attr=paddle.ParamAttr(initializer=Constant(value=0.0)),
                                bias_attr=paddle.ParamAttr(initializer=Constant(value=0.0)))
        self.fc2 = nn.Linear(hidden_size, output_size,
                                weight_attr=paddle.ParamAttr(initializer=Constant(value=0.0)),
                                bias_attr=paddle.ParamAttr(initializer=Constant(value=0.0)))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = F.sigmoid
        
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

def print_weights(runner):
    print('The weights of the Layers：')
    
    for item in runner.model.sublayers():
        print(item.full_name())
        for param in item.parameters():
            print(param.numpy())
        

利用Runner类训练模型：

# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V4(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 设置损失函数
loss_fn = F.binary_cross_entropy

# 设置优化器
learning_rate = 0.2 #5e-2
optimizer = paddle.optimizer.SGD(learning_rate=learning_rate, parameters=model.parameters())

# 设置评价指标
metric = accuracy

# 其他参数
epoch = 2000
saved_path = 'best_model.pdparams'

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=5, log_epochs=50, save_path="best_model.pdparams",custom_print_log=print_weights)

可视化训练和验证集上的主准确率和loss变化：

plot(runner, "fw-zero.pdf")

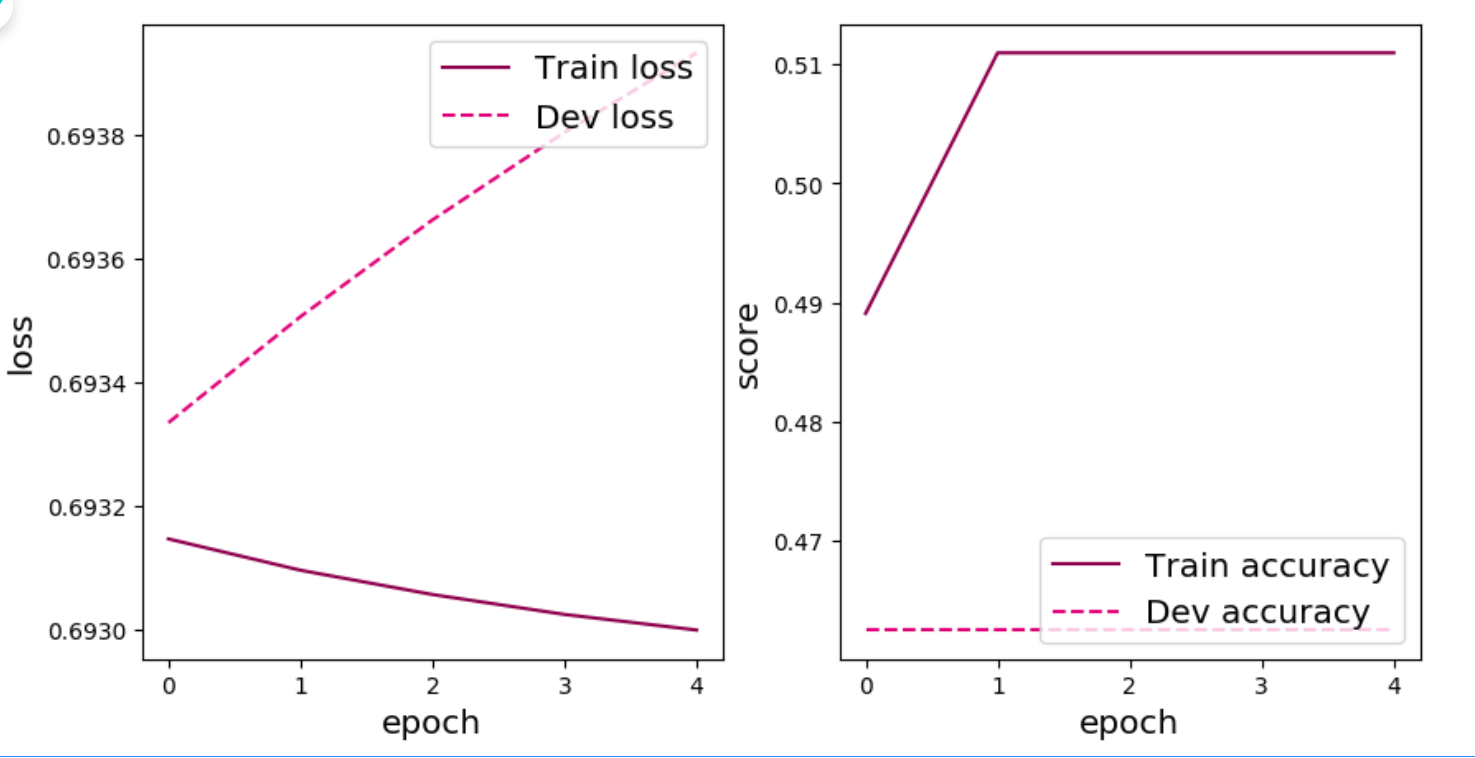
==从输出结果看，二分类准确率为50%左右，说明模型没有学到任何内容。训练和验证loss几乎没有怎么下降。==

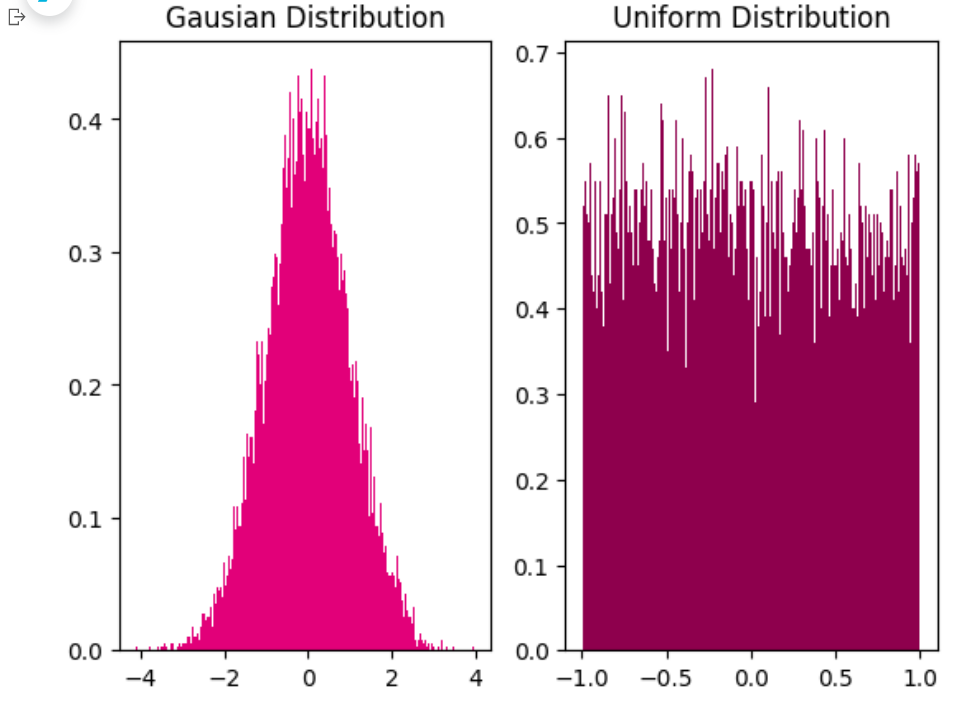
==为了避免对称权重现象，可以使用高斯分布或均匀分布初始化神经网络的参数。==

高斯分布和均匀分布采样的实现和可视化代码如下：

# 使用'paddle.normal'实现高斯分布采样，其中'mean'为高斯分布的均值，'std'为高斯分布的标准差，'shape'为输出形状
gausian_weights = paddle.normal(mean=0.0, std=1.0, shape=[10000])
# 使用'paddle.uniform'实现在[min,max)范围内的均匀分布采样，其中'shape'为输出形状
uniform_weights = paddle.uniform(shape=[10000], min=- 1.0, max=1.0)

# 绘制两种参数分布
plt.figure()
plt.subplot(1,2,1)
plt.title('Gausian Distribution')
plt.hist(gausian_weights, bins=200, density=True, color='#E20079')
plt.subplot(1,2,2)
plt.title('Uniform Distribution')
plt.hist(uniform_weights, bins=200, density=True, color='#8E004D')
plt.savefig('fw-gausian-uniform.pdf')
plt.show()

alec总结：

如果网络的参数初始化的时候，将其全部初始化为0，那么将学不到任何东西。因此需要通过高斯分布、均匀分布等初始化，而不能直接全零初始化。

---

[√] 4.4.2 - 梯度消失问题

alec记录：

（1）随着网络层数的加深，容易出现梯度消失的问题。

（2）对于sigmoid型的激活函数，这种函数在饱和区（x趋向于很大或者很小）的时候，梯度很小，再加上网络层数很深，误差不断的衰减，因此最终梯度很小，就出现了梯度消失问题。解决这种问题的简单有效的方法之一是使用导数比较大的激活函数，比如ReLU激活函数。（ReLU激活函数在x为正的时候，梯度始终等于1，因此能够处理梯度消失问题。）

在神经网络的构建过程中，随着网络层数的增加，理论上网络的拟合能力也应该是越来越好的。但是随着网络变深，参数学习更加困难，容易出现梯度消失问题。

由于Sigmoid型函数的饱和性，饱和区的导数更接近于0，误差经过每一层传递都会不断衰减。当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练，这就是所谓的梯度消失问题。 在深度神经网络中，减轻梯度消失问题的方法有很多种，一种简单有效的方式就是使用导数比较大的激活函数，如：ReLU。

下面通过一个简单的实验观察前馈神经网络的梯度消失现象和改进方法。

---

#####[√] 4.4.2.1 - 模型构建

定义一个前馈神经网络，包含4个隐藏层和1个输出层，通过传入的参数指定激活函数。代码实现如下：

# 定义多层前馈神经网络
class Model_MLP_L5(paddle.nn.Layer):
    def __init__(self, input_size, output_size, act='sigmoid', w_init=Normal(mean=0.0, std=0.01), b_init=Constant(value=1.0)):
        super(Model_MLP_L5, self).__init__()
        self.fc1 = paddle.nn.Linear(input_size, 3)
        self.fc2 = paddle.nn.Linear(3, 3)
        self.fc3 = paddle.nn.Linear(3, 3)
        self.fc4 = paddle.nn.Linear(3, 3)
        self.fc5 = paddle.nn.Linear(3, output_size)
        # 定义网络使用的激活函数
        if act == 'sigmoid':
            self.act = F.sigmoid
        elif act == 'relu':
            self.act = F.relu
        elif act == 'lrelu':
            self.act = F.leaky_relu
        else:
            raise ValueError("Please enter sigmoid, relu or lrelu!")
        # 初始化线性层权重和偏置参数
        self.init_weights(w_init, b_init)

    # 初始化线性层权重和偏置参数（初始化的是线性层的参数，不含激活层（非线性层）的参数）
    def init_weights(self, w_init, b_init):
        # 使用'named_sublayers'遍历所有网络层
        for n, m in self.named_sublayers():
            # 如果是线性层，则使用指定方式进行参数初始化
            if isinstance(m, nn.Linear):
                w_init(m.weight)
                b_init(m.bias)

    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        outputs = self.act(outputs)
        outputs = self.fc3(outputs)
        outputs = self.act(outputs)
        outputs = self.fc4(outputs)
        outputs = self.act(outputs)
        outputs = self.fc5(outputs)
        outputs = F.sigmoid(outputs)
        return outputs

---

[√] 4.4.2.2 - 使用Sigmoid型函数进行训练

使用Sigmoid型函数作为激活函数，为了便于观察梯度消失现象，只进行一轮网络优化。代码实现如下：

定义梯度打印函数：

def print_grads(runner):
    # 打印每一层的权重的模
    print('The gradient of the Layers：')
    for item in runner.model.sublayers():
        if len(item.parameters())==2:
            print(item.full_name(), paddle.norm(item.parameters()[0].grad, p=2.).numpy()[0])

paddle.seed(102)
# 学习率大小
lr = 0.01

# 定义网络，激活函数使用sigmoid
model =  Model_MLP_L5(input_size=2, output_size=1, act='sigmoid')

# 定义优化器
optimizer = paddle.optimizer.SGD(learning_rate=lr, parameters=model.parameters())

# 定义损失函数，使用交叉熵损失函数
loss_fn = F.binary_cross_entropy

# 定义评价指标
metric = accuracy

# 指定梯度打印函数
custom_print_log=print_grads

实例化RunnerV2_2类，并传入训练配置。代码实现如下：

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

模型训练，打印网络每层梯度值的$\ell_2$范数。代码实现如下：

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], 
            num_epochs=1, log_epochs=None, 
            save_path="best_model.pdparams", 
            custom_print_log=custom_print_log)

The gradient of the Layers：
linear_2 0.0007373723
linear_3 0.006756582

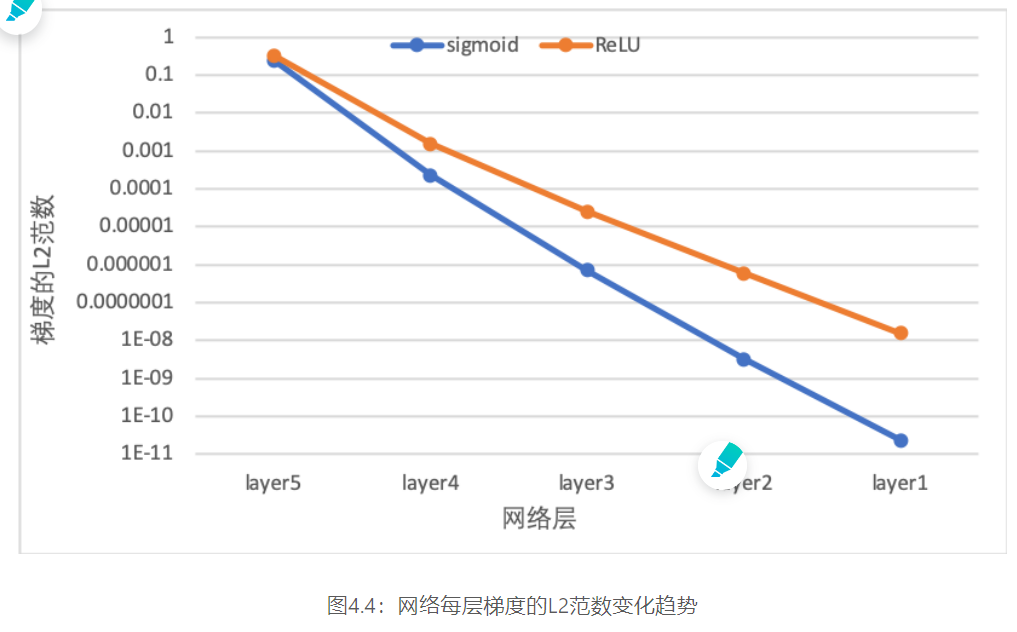
观察实验结果可以发现，梯度经过每一个神经层的传递都会不断衰减，最终传递到第一个神经层时，梯度几乎完全消失。

alec分析：

使用sigmoid型的激活函数，随着网络的加深，出现了梯度消失的现象，这可能导致网络无法继续学习下去。因此梯度为0，无法更新参数了。

---

[√] 4.4.2.3 - 使用ReLU函数进行模型训练

paddle.seed(102)
lr = 0.01  # 学习率大小

# 定义网络，激活函数使用relu
model =  Model_MLP_L5(input_size=2, output_size=1, act='relu') # 使用ReLU作为激活函数

# 定义优化器
optimizer = paddle.optimizer.SGD(learning_rate=lr, parameters=model.parameters())

# 定义损失函数
# 定义损失函数，这里使用交叉熵损失函数
loss_fn = F.binary_cross_entropy

# 定义评估指标
metric = accuracy

# 实例化Runner
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], 
            num_epochs=1, log_epochs=None, 
            save_path="best_model.pdparams", 
            custom_print_log=custom_print_log)

The gradient of the Layers：
linear_9 4.828196e-08
linear_10 3.2609435e-06
linear_11 0.0001859922
linear_12 0.011442569
linear_13 0.43247733
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.53750

图4.4 展示了使用不同激活函数时，网络每层梯度值的ℓ2\ell_2ℓ2范数情况。从结果可以看到，5层的全连接前馈神经网络使用Sigmoid型函数作为激活函数时，梯度经过每一个神经层的传递都会不断衰减，最终传递到第一个神经层时，梯度几乎完全消失。改为ReLU激活函数后，梯度消失现象得到了缓解，每一层的参数都具有梯度值。

alec结论：

使用ReLU激活函数能够较好的解决使用sigmoid激活函数导致的梯度消失问题。

---

[√] 4.4.3 - 死亡 ReLU 问题

==ReLU函数的利与弊：ReLU激活函数可以一定程度上改善梯度消失问题，但是ReLU函数在某些情况下容易出现死亡 ReLU问题，使得网络难以训练。==

这是由于当$x<0$时，ReLU函数的输出恒为0。在训练过程中，如果参数在一次不恰当的更新后，某个ReLU神经元在所有训练数据上都不能被激活（即输出为0），那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远都不能被激活。而一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU的变种。

alec：

因为ReLU函数在x轴的负数部分恒为0，因此这就导致梯度永远是0，出现了死亡梯度问题。

解决这个问题的方法就是，将负半轴改变，例如可以使用Leaky ReLU、ELU等ReLU的变种。

---

[√] 4.4.3.1 - 使用ReLU进行模型训练

使用第4.4.2节中定义的多层全连接前馈网络进行实验，使用ReLU作为激活函数，观察死亡ReLU现象和优化方法。当神经层的偏置被初始化为一个相对于权重较大的负值时，可以想像，输入经过神经层的处理，最终的输出会为负值，从而导致死亡ReLU现象。

# 定义网络，并使用较大的负值来初始化偏置
model =  Model_MLP_L5(input_size=2, output_size=1, act='relu', b_init=Constant(value=-8.0))

实例化RunnerV2类，启动模型训练，打印网络每层梯度值的$\ell_2$范数。代码实现如下：

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], 
            num_epochs=1, log_epochs=0, 
            save_path="best_model.pdparams", 
            custom_print_log=custom_print_log)

The gradient of the Layers：
linear_14 0.0
linear_15 0.0
linear_16 0.0
linear_17 0.0
linear_18 0.0
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50625

从输出结果可以发现，使用 ReLU 作为激活函数，当满足条件时，会发生死亡ReLU问题，网络训练过程中 ReLU 神经元的梯度始终为0，参数无法更新。

针对死亡ReLU问题，一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU 的变种。接下来，观察将激活函数更换为 Leaky ReLU时的梯度情况。

---

[√] 4.4.3.2 - 使用Leaky ReLU进行模型训练

将激活函数更换为Leaky ReLU进行模型训练，观察梯度情况。代码实现如下：

# 重新定义网络，使用Leaky ReLU激活函数
model =  Model_MLP_L5(input_size=2, output_size=1, act='lrelu', b_init=Constant(value=-8.0))

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], 
            num_epochs=1, log_epochps=None, 
            save_path="best_model.pdparams", 
            custom_print_log=custom_print_log)

The gradient of the Layers：
linear_19 2.0111758e-16
linear_20 1.8527564e-13
linear_21 1.6659853e-09
linear_22 1.1705935e-05
linear_23 0.06902571
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50625
[Train] epoch: 0/1, loss: 3.988154649734497

从输出结果可以看到，将激活函数更换为Leaky ReLU后，死亡ReLU问题得到了改善，梯度恢复正常，参数也可以正常更新。但是由于 Leaky ReLU 中，$\mathcal{x<0}$ 时的斜率默认只有0.01，所以反向传播时，随着网络层数的加深，梯度值越来越小。如果想要改善这一现象，将 Leaky ReLU 中，$\mathcal{x<0}$ 时的斜率调大即可。

[√] 4.5 - 实践：基于前馈神经网络完成鸢尾花分类

在本实践中，我们继续使用第三章中的鸢尾花分类任务，将Softmax分类器替换为本章介绍的前馈神经网络。 在本实验中，我们使用的损失函数为交叉熵损失；优化器为随机梯度下降法；评价指标为准确率。

---

[√] 4.5.1 - 小批量梯度下降法

在梯度下降法中，目标函数是整个训练集上的风险函数，这种方式称为批量梯度下降法（Batch Gradient Descent，BGD）。 批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和。当训练集中的样本数量NNN很大时，空间复杂度比较高，每次迭代的计算开销也很大。

为了减少每次迭代的计算复杂度，我们可以在每次迭代时只采集一小部分样本，计算在这组样本上损失函数的梯度并更新参数，这种优化方式称为 小批量梯度下降法（Mini-Batch Gradient Descent，Mini-Batch GD）。

第$t$次迭代时，随机选取一个包含$K$个样本的子集$\mathcal{B}t$，计算这个子集上每个样本损失函数的梯度并进行平均，然后再进行参数更新。
$$
\theta{t+1} \leftarrow \theta_t - \alpha \frac{1}{K} \sum_{(\boldsymbol{x},y)\in \mathcal{S}_t} \frac{\partial \mathcal{L}\Big(y,f(\boldsymbol{x};\theta)\Big)}{\partial \theta},
$$
==其中$K$为**批量大小(Batch Size)**。$K$通常不会设置很大，一般在$1\sim100$之间。==

==在实际应用中为了提高计算效率，通常设置为2的幂$2^n$。==

==在实际应用中，小批量随机梯度下降法有收敛快、计算开销小的优点，因此逐渐成为大规模的机器学习中的主要优化算法。==
==此外，随机梯度下降相当于在批量梯度下降的梯度上引入了随机噪声。在非凸优化问题中，随机梯度下降更容易逃离局部最优点。==

alec:

小批量梯度下降收敛快、开销小。

随机梯度下降在梯度下降的基础上引入了随机噪声，因此更加容易逃离局部最优点。

小批量随机梯度下降法的训练过程如下：

---

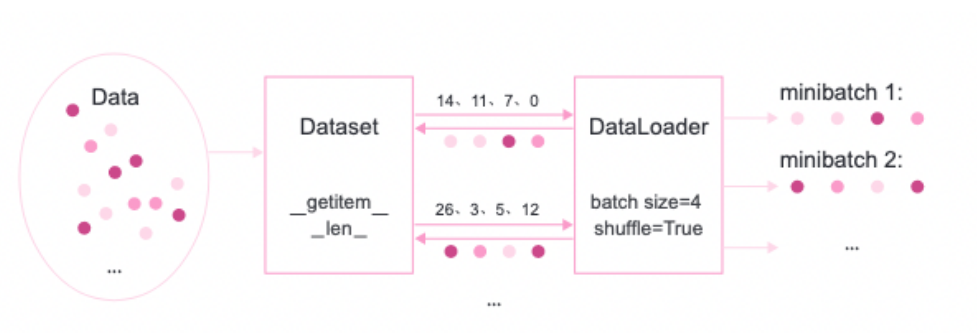
[√] 4.5.1.1 - 数据分组

==为了小批量梯度下降法，我们需要对数据进行随机分组。目前，机器学习中通常做法是构建一个数据迭代器，每个迭代过程中从全部数据集中获取一批指定数量的数据。==

数据迭代器的实现原理如下图所示：

1. 首先，将数据集封装为Dataset类，传入一组索引值，根据索引从数据集合中获取数据；
2. 其次，构建DataLoader类，需要指定数据批量的大小和是否需要对数据进行乱序，通过该类即可批量获取数据。

在实践过程中，通常使用进行参数优化。在飞桨中，使用paddle.io.DataLoader加载minibatch的数据， paddle.io.DataLoader API可以生成一个迭代器，其中通过设置batch_size参数来指定minibatch的长度，通过设置shuffle参数为True，可以在生成minibatch的索引列表时将索引顺序打乱。

---

[√] 4.5.2 - 数据处理

构造IrisDataset类进行数据读取，继承自paddle.io.Dataset类。paddle.io.Dataset是用来封装 Dataset的方法和行为的抽象类，通过一个索引获取指定的样本，同时对该样本进行数据处理。当继承paddle.io.Dataset来定义数据读取类时，实现如下方法：

• __getitem__：根据给定索引获取数据集中指定样本，并对样本进行数据处理；
• __len__：返回数据集样本个数。

代码实现如下：

import numpy as np
import paddle
import paddle.io as io
from nndl.dataset import load_data

class IrisDataset(io.Dataset):
    def __init__(self, mode='train', num_train=120, num_dev=15):
        super(IrisDataset, self).__init__()
        # 调用第三章中的数据读取函数，其中不需要将标签转成one-hot类型
        X, y = load_data(shuffle=True)
        if mode == 'train':
            self.X, self.y = X[:num_train], y[:num_train]
        elif mode == 'dev':
            self.X, self.y = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
        else:
            self.X, self.y = X[num_train + num_dev:], y[num_train + num_dev:]

    def __getitem__(self, idx):
        return self.X[idx], self.y[idx]

    def __len__(self):
        return len(self.y)

paddle.seed(12)
train_dataset = IrisDataset(mode='train')
dev_dataset = IrisDataset(mode='dev')
test_dataset = IrisDataset(mode='test')

# 打印训练集长度
print ("length of train set: ", len(train_dataset))

---

[√] 4.5.2.2 - 用DataLoader进行封装

# 批量大小
batch_size = 16

# 加载数据
train_loader = io.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = io.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = io.DataLoader(test_dataset, batch_size=batch_size)

---

[√] 4.5.3 - 模型构建

构建一个简单的前馈神经网络进行鸢尾花分类实验。其中输入层神经元个数为4，输出层神经元个数为3，隐含层神经元个数为6。代码实现如下：

from paddle import nn

# 定义前馈神经网络
class Model_MLP_L2_V3(nn.Layer):
    def __init__(self, input_size, output_size, hidden_size):
        super(Model_MLP_L2_V3, self).__init__()
        # 构建第一个全连接层
        self.fc1 = nn.Linear(
            input_size,
            hidden_size,
            weight_attr=paddle.ParamAttr(initializer=nn.initializer.Normal(mean=0.0, std=0.01)),
            bias_attr=paddle.ParamAttr(initializer=nn.initializer.Constant(value=1.0))
        )
        # 构建第二全连接层
        self.fc2 = nn.Linear(
            hidden_size,
            output_size,
            weight_attr=paddle.ParamAttr(initializer=nn.initializer.Normal(mean=0.0, std=0.01)),
            bias_attr=paddle.ParamAttr(initializer=nn.initializer.Constant(value=1.0))
        )
        # 定义网络使用的激活函数
        self.act = nn.Sigmoid()

    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        return outputs

fnn_model = Model_MLP_L2_V3(input_size=4, output_size=3, hidden_size=6)

---

[√] 4.5.4 - 完善Runner类

==基于RunnerV2类进行完善实现了RunnerV3类。其中训练过程使用自动梯度计算==

==使用DataLoader加载批量数据==

==使用随机梯度下降法进行参数优化==

模型保存时，使用state_dict方法获取模型参数

模型加载时，使用set_state_dict方法加载模型参数.

==由于这里使用随机梯度下降法对参数优化，所以数据以批次的形式输入到模型中进行训练==

==那么评价指标计算也是分别在每个批次进行的==

==要想获得每个epoch整体的评价结果，需要对历史评价结果进行累积。==

这里定义Accuracy类实现该功能。

from paddle.metric import Metric

class Accuracy(Metric):
    def __init__(self, is_logist=True):
        """
        输入：
           - is_logist: outputs是logist还是激活后的值
        """

        # 用于统计正确的样本个数
        self.num_correct = 0
        # 用于统计样本的总数
        self.num_count = 0

        self.is_logist = is_logist

    def update(self, outputs, labels):
        """
        输入：
           - outputs: 预测值, shape=[N,class_num]
           - labels: 标签值, shape=[N,1]
        """

        # 判断是二分类任务还是多分类任务，shape[1]=1时为二分类任务，shape[1]>1时为多分类任务
        if outputs.shape[1] == 1: # 二分类
            outputs = paddle.squeeze(outputs, axis=-1)
            if self.is_logist:
                # logist判断是否大于0
                preds = paddle.cast((outputs>=0), dtype='float32')
            else:
                # 如果不是logist，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
                preds = paddle.cast((outputs>=0.5), dtype='float32')
        else:
            # 多分类时，使用'paddle.argmax'计算最大元素索引作为类别
            preds = paddle.argmax(outputs, axis=1, dtype='int64')

        # 获取本批数据中预测正确的样本个数
        labels = paddle.squeeze(labels, axis=-1)
        batch_correct = paddle.sum(paddle.cast(preds==labels, dtype="float32")).numpy()[0]
        batch_count = len(labels)

        # 更新num_correct 和 num_count
        self.num_correct += batch_correct
        self.num_count += batch_count

    def accumulate(self):
        # 使用累计的数据，计算总的指标
        if self.num_count == 0:
            return 0
        return self.num_correct / self.num_count

    def reset(self):
        # 重置正确的数目和总数
        self.num_correct = 0
        self.num_count = 0

    def name(self):
        return "Accuracy"

RunnerV3类的代码实现如下：

import paddle.nn.functional as F

class RunnerV3(object):
    def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric # 只用于计算评价指标

        # 记录训练过程中的评价指标变化情况
        self.dev_scores = []

        # 记录训练过程中的损失函数变化情况
        self.train_epoch_losses = [] # 一个epoch记录一次loss
        self.train_step_losses = []  # 一个step记录一次loss
        self.dev_losses = []
        
        # 记录全局最优指标
        self.best_score = 0

    def train(self, train_loader, dev_loader=None, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_steps = kwargs.get("log_steps", 100)
        # 评价频率
        eval_steps = kwargs.get("eval_steps", 0)

        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        custom_print_log = kwargs.get("custom_print_log", None) 
       
        # 训练总的步数
        # len(train_loader)为 mini-batch 的数量
        num_training_steps = num_epochs * len(train_loader)

        if eval_steps:
            if self.metric is None:
                raise RuntimeError('Error: Metric can not be None!')
            if dev_loader is None:
                raise RuntimeError('Error: dev_loader can not be None!')
            
        # 运行的step数目
        global_step = 0

        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            # 用于统计训练集的损失
            total_loss = 0
            for step, data in enumerate(train_loader):
                X, y = data
                # 获取模型预测
                logits = self.model(X)
                loss = self.loss_fn(logits, y) # 默认求mean
                total_loss += loss # 统计累加损失

                # 训练过程中，每个step的loss进行保存
                self.train_step_losses.append((global_step,loss.item()))

                if log_steps and global_step%log_steps==0:
                    print(f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")
                
                # 梯度反向传播，计算每个参数的梯度值
                # alec：计算每个参数的梯度
                loss.backward() 

                if custom_print_log:
                   custom_print_log(self)
                
                # 小批量梯度下降进行参数更新
                # 更新参数
                self.optimizer.step()
                # 梯度归零
                # 梯度归零
                self.optimizer.clear_grad()

                # 判断是否需要评价
                if eval_steps>0 and global_step>0 and \
                    (global_step%eval_steps == 0 or global_step==(num_training_steps-1)):

                    dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
                    print(f"[Evaluate]  dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}") 

                    # 将模型切换为训练模式
                    self.model.train()

                    # 如果当前指标为最优指标，保存该模型
                    # 通过计算在验证集上的验证得分来判断是否是最优的模型
                    if dev_score > self.best_score:
                        self.save_model(save_path)
                        print(f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
                        self.best_score = dev_score

                global_step += 1
            
            # 当前epoch 训练loss累计值 
            # 当前epoch的损失的平均值
            trn_loss = (total_loss / len(train_loader)).item()
            # epoch粒度的训练loss保存
            self.train_epoch_losses.append(trn_loss)
            
        print("[Train] Training done!")

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    # 评估阶段，不需要计算和存储梯度
    @paddle.no_grad()
    def evaluate(self, dev_loader, **kwargs):
        assert self.metric is not None

        # 将模型设置为评估模式
        self.model.eval()

        global_step = kwargs.get("global_step", -1) 

        # 用于统计训练集的损失
        total_loss = 0

        # 重置评价
        self.metric.reset() 
        
        # 遍历验证集每个批次  
        # alec：第一个参数是指第几个mini-batch，第二个参数是存储该批次的数据对
        for batch_id, data in enumerate(dev_loader):
            X, y = data
    
            # 计算模型输出
            logits = self.model(X)
            
            # 计算损失函数
            loss = self.loss_fn(logits, y).item()
            # 累积损失
            total_loss += loss 

            # 累积评价
            self.metric.update(logits, y)

        dev_loss = (total_loss/len(dev_loader))
        dev_score = self.metric.accumulate() 

        # 记录验证集loss
        if global_step!=-1:
            self.dev_losses.append((global_step, dev_loss))
            self.dev_scores.append(dev_score)
        
        return dev_score, dev_loss
    
    # 模型预测阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @paddle.no_grad()
    def predict(self, x, **kwargs):
        # 将模型设置为评估模式
        self.model.eval()
        # 运行模型前向计算，得到预测值
        logits = self.model(x)
        return logits

    def save_model(self, save_path):
        paddle.save(self.model.state_dict(), save_path)

    def load_model(self, model_path):
        model_state_dict = paddle.load(model_path)
        self.model.set_state_dict(model_state_dict)

---

[√] 4.5.5 - 模型训练

实例化RunnerV3类，并传入训练配置，代码实现如下：

import paddle.optimizer as opt

lr = 0.2

# 定义网络
model = fnn_model

# 定义优化器
optimizer = opt.SGD(learning_rate=lr, parameters=model.parameters())

# 定义损失函数。softmax+交叉熵
loss_fn = F.cross_entropy

# 定义评价指标
metric = Accuracy(is_logist=True)

runner = RunnerV3(model, optimizer, loss_fn, metric)

使用训练集和验证集进行模型训练，共训练150个epoch。在实验中，保存准确率最高的模型作为最佳模型。代码实现如下：

# 启动训练
log_steps = 100
eval_steps = 50
runner.train(train_loader, dev_loader, 
            num_epochs=150, log_steps=log_steps, eval_steps = eval_steps,
            save_path="best_model.pdparams") 

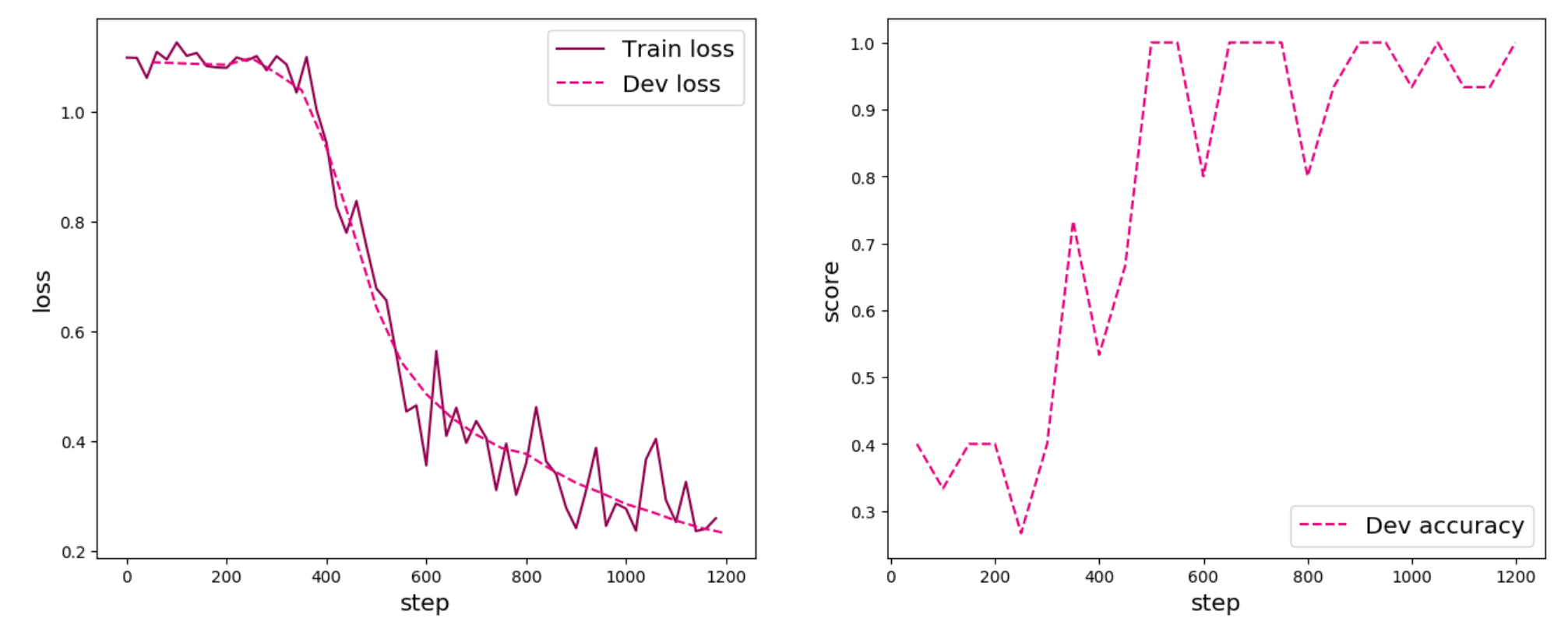
[Train] epoch: 0/150, step: 0/1200, loss: 1.09866
[Evaluate]  dev score: 0.40000, dev loss: 1.09026
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.40000
[Train] epoch: 12/150, step: 100/1200, loss: 1.12618
[Evaluate]  dev score: 0.33333, dev loss: 1.08850
[Evaluate]  dev score: 0.40000, dev loss: 1.08677
[Train] epoch: 25/150, step: 200/1200, loss: 1.08003
[Evaluate]  dev score: 0.40000, dev loss: 1.08576
[Evaluate]  dev score: 0.26667, dev loss: 1.09782
[Train] epoch: 37/150, step: 300/1200, loss: 1.10121
[Evaluate]  dev score: 0.40000, dev loss: 1.06987
[Evaluate]  dev score: 0.73333, dev loss: 1.03954
[Evaluate] best accuracy performence has been updated: 0.40000 --> 0.73333
[Train] epoch: 50/150, step: 400/1200, loss: 0.94351
[Evaluate]  dev score: 0.53333, dev loss: 0.93444
[Evaluate]  dev score: 0.66667, dev loss: 0.79328
[Train] epoch: 62/150, step: 500/1200, loss: 0.67799
[Evaluate]  dev score: 1.00000, dev loss: 0.64378
[Evaluate] best accuracy performence has been updated: 0.73333 --> 1.00000
[Evaluate]  dev score: 1.00000, dev loss: 0.54416
[Train] epoch: 75/150, step: 600/1200, loss: 0.35588
[Evaluate]  dev score: 0.80000, dev loss: 0.48563
[Evaluate]  dev score: 1.00000, dev loss: 0.44295
[Train] epoch: 87/150, step: 700/1200, loss: 0.43655
[Evaluate]  dev score: 1.00000, dev loss: 0.41185
[Evaluate]  dev score: 1.00000, dev loss: 0.38773
[Train] epoch: 100/150, step: 800/1200, loss: 0.35982
[Evaluate]  dev score: 0.80000, dev loss: 0.37680
[Evaluate]  dev score: 0.93333, dev loss: 0.34835
[Train] epoch: 112/150, step: 900/1200, loss: 0.24126
[Evaluate]  dev score: 1.00000, dev loss: 0.32392
[Evaluate]  dev score: 1.00000, dev loss: 0.30578
[Train] epoch: 125/150, step: 1000/1200, loss: 0.27697
[Evaluate]  dev score: 0.93333, dev loss: 0.28536
[Evaluate]  dev score: 1.00000, dev loss: 0.27146
[Train] epoch: 137/150, step: 1100/1200, loss: 0.25255
[Evaluate]  dev score: 0.93333, dev loss: 0.25523
[Evaluate]  dev score: 0.93333, dev loss: 0.24195
[Evaluate]  dev score: 1.00000, dev loss: 0.23231
[Train] Training done!

可视化观察训练集损失和训练集loss变化情况。

import matplotlib.pyplot as plt

# 绘制训练集和验证集的损失变化以及验证集上的准确率变化曲线
def plot_training_loss_acc(runner, fig_name, 
    fig_size=(16, 6), 
    sample_step=20, 
    loss_legend_loc="upper right", 
    acc_legend_loc="lower right",
    train_color="#8E004D",
    dev_color='#E20079',
    fontsize='x-large',
    train_linestyle="-",
    dev_linestyle='--'):

    plt.figure(figsize=fig_size)

    plt.subplot(1,2,1)
    train_items = runner.train_step_losses[::sample_step]
    train_steps=[x[0] for x in train_items]
    train_losses = [x[1] for x in train_items]

    plt.plot(train_steps, train_losses, color=train_color, linestyle=train_linestyle, label="Train loss")
    if len(runner.dev_losses)>0:
        dev_steps=[x[0] for x in runner.dev_losses]
        dev_losses = [x[1] for x in runner.dev_losses]
        plt.plot(dev_steps, dev_losses, color=dev_color, linestyle=dev_linestyle, label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize=fontsize)
    plt.xlabel("step", fontsize=fontsize)
    plt.legend(loc=loss_legend_loc, fontsize=fontsize)

    # 绘制评价准确率变化曲线
    if len(runner.dev_scores)>0:
        plt.subplot(1,2,2)
        plt.plot(dev_steps, runner.dev_scores,
            color=dev_color, linestyle=dev_linestyle, label="Dev accuracy")
    
        # 绘制坐标轴和图例
        plt.ylabel("score", fontsize=fontsize)
        plt.xlabel("step", fontsize=fontsize)
        plt.legend(loc=acc_legend_loc, fontsize=fontsize)

    plt.savefig(fig_name)
    plt.show()

plot_training_loss_acc(runner, 'fw-loss.pdf')

从输出结果可以看出准确率随着迭代次数增加逐渐上升，损失函数下降。

---

[√] 4.5.6 - 模型评价

使用测试数据对在训练过程中保存的最佳模型进行评价，观察模型在测试集上的准确率以及Loss情况。代码实现如下：

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))

[Test] accuracy/loss: 0.8000/0.6891

---

[√] 4.5.7 - 模型预测

同样地，也可以使用保存好的模型，对测试集中的某一个数据进行模型预测，观察模型效果。代码实现如下：

# 获取测试集中第一条数据
X, label = next(test_loader())
logits = runner.predict(X)

pred_class = paddle.argmax(logits[0]).numpy()
label = label[0][0].numpy()

# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))

The true category is [2] and the predicted category is [2]

---

[√] 4.6 - 小结

本章介绍前馈神经网络的基本概念、网络结构及代码实现，利用前馈神经网络完成一个分类任务，并通过两个简单的实验，观察前馈神经网络的梯度消失问题和死亡ReLU问题，以及对应的优化策略。 此外，还实践了基于前馈神经网络完成鸢尾花分类任务。

---

[√] 4.7 - 实验拓展

尝试基于MNIST手写数字识别数据集，设计合适的前馈神经网络进行实验，并取得95%以上的准确率。

---